PSO算法在氯盐环境结构耐久性评定中的应用

杨厚易，张 凯，过民龙

（广东省建筑科学研究院集团股份有限公司 广州 510500）

0 引言

南方沿海地区的钢筋混凝土结构长期处于高氯盐侵蚀环境之中，氯盐环境下的结构耐久性评定是近年来日益受到重视的一项性能指标，各国每年花费大量资金、人力和时间用于修复受氯盐侵蚀的道路和桥梁，修复这些建筑物的费用往往超过了其建造费用，因此，氯盐侵蚀环境下的钢筋混凝土结构耐久性相关评定方法受到科研人员、结构设计者、维护人员的广泛关注。

氯盐环境是混泥土结构在服役过程中的一种危险环境，环境中氯离子穿透保护层到达钢筋表面造成钢筋锈蚀，进而引起结构胀裂［1］。各国通过研究氯离子在混泥土内的运动规律，提出了各种模型来预测内部钢筋的脱钝时间与保护层开裂时间［2-4］。西安建筑科技大学的牛荻涛等人针对混凝土结构耐久性起草了相关评定标准，于2007年由中国工程建设标准化协会批准发布，即《混凝土结构耐久性评定标准：CECS 220∶2007》［5］。2019 年，《既有混凝土结构耐久性评定标准：GB/T 51355—2019》［6］对文献［5］中的内容进行了修订和补充。但文献［5］与文献［6］中，对于氯盐环境下的混凝土钢筋脱钝时间与保护层锈胀开裂时间的计算模型十分复杂，难以通过整理公式获得解析解，对标准的推广与应用带来不便。对于这类难以获得解析解的模型公式，通常采用数值进化算法［7］进行求解，但数值进化算法存在局部最优、求解结果不稳定、运算时间不确定等一系列问题，使得数值进化算法存在计算风险。本文对文献［5］与文献［6］中难以获得解析解的钢筋脱钝模型与保护层锈胀开裂模型构建了目标函数，并通过进化算法中最具有代表性的PSO 算法［8-10］对目标函数进行了求解，分析了PSO 算法对于氯盐环境下钢筋混凝土耐久性评定中的稳定性、安全性、可用性。

1 目标函数的构建

1.1 钢筋脱钝模型目标函数的构建

在文献［5］与文献［6］中，进行氯盐环境下钢筋混凝土耐久性评估的一个难点在于对钢筋脱钝时间和保护层锈胀开裂时间的计算。钢筋脱钝时间ti的计算模型如下所示：

当ti≤t1时，ti可由式⑴求得：

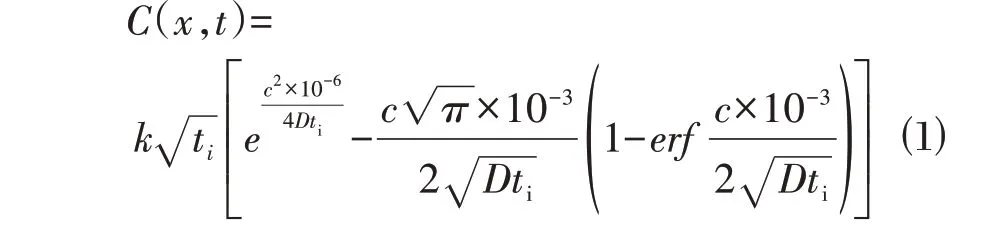
当ti＞t1时，ti=t1+t2，t2通过式⑵与式⑶求得：

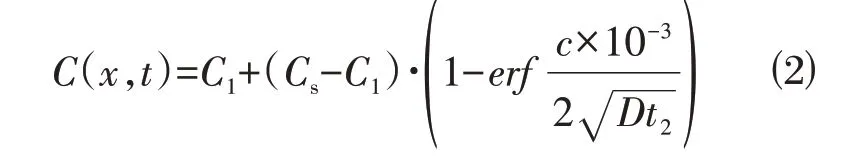
式⑵中：

式中：ti为钢筋脱钝时间（a）；t1为混凝土表面氯离子浓度稳定时间（a）；c为混凝土保护层厚度（mm）；D为氯离子扩散系数（m2/a）；C（x，t）为t时刻检测时x深度处的氯离子浓度（kg/m3）；Cs为实测混凝土表面氯离子浓度（kg/m3）；

式⑴～⑶可知，获得钢筋脱钝时间ti的解析解十分困难。为了求解上述模型，本文首先构建了模型的目标函数，再利用PSO 算法对目标函数进行优化，从而完成对模型的求解。对式⑴进行整理，ti≤t1时，钢筋托钝时间误差函数如式⑷所示，其中△E（ti）ti>t1为误差函数值：

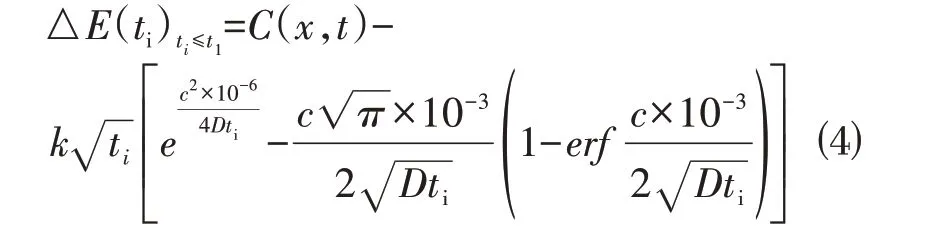
根据误差函数，钢筋脱钝时间的目标函数如式⑸所示，其中E（ti）ti≤t1的最优解即是误差函数值△E（ti）ti≤t1最接近0时的参数ti：

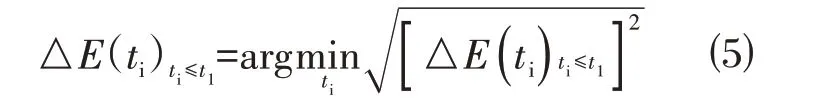
同理，当ti＞t1时，ti=t1+t2，其中t1为定值，在ti＞t1的情况下，模型ti的求解问题就转变为了对t2的求解，因此对式⑶进行整理，t2的误差函数如式⑹所示：

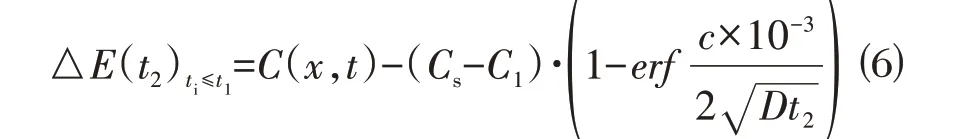
当ti＞t1时，t2目标函数为：

1.2 保护层锈胀开裂模型目标函数的构建

对于保护层锈胀开裂时间tcr的计算公式如下：

其中ti为钢筋脱钝时间；tc为钢筋开始锈蚀至保护层开裂时间。tc的计算方法如式⑼所示，其中δcr为保护层开裂时的钢筋临界锈蚀深度；λcl为氯盐侵蚀环境下保护层开裂前钢筋平均年锈蚀速率：

保护层开裂时的钢筋临界锈蚀深度δcr可根据钢筋直径、保护层厚度、混凝土抗压强度标准值进行计算，在构建目标函数时，可将该值钱视为定值。而λcl则根据式⑽进行估算：

式中：i为钢筋腐蚀电流密度。

钢筋腐蚀电流密度的计算公式为：

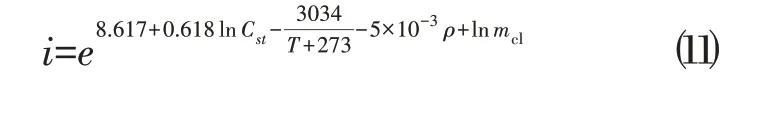
式中：Csl为钢筋表面氯离子浓度（kg/m3）；mcl为局部环境系数；ρ为混凝土电阻率（KΩ/cm）。

而钢筋表面氯离子浓度Csl如式⑿所示：

其中Cs0为混凝土制备时氯离子的掺入量；c为保护层厚度。结合式⑻～⑿，想要对保护层锈胀开裂时间tcr进行求解，需要求解钢筋腐蚀电流密度，而求解钢筋腐蚀电流密度则需要求解钢筋表面氯离子浓度Csl，即式⑿，这是又是一个关于tcr的函数。因此，要得到tcr的解析解是十分困难的。

结合式⑻～⑿可得tcr的误差函数△E（tcr）：

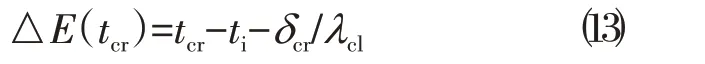
tcr的目标函数则可表示为：

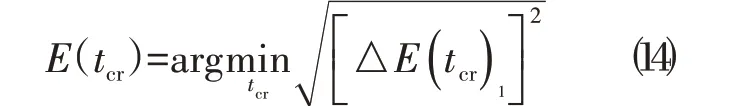
2 PSO算法的求解

2.1 问题的抽象

数值进化算法借鉴了大自然中生物的行为或物理现象，如种群进化、鱼群觅食、鸟类捕食等。PSO 算法则是最具代表性的一种数值进化算法，其具有广泛的适用性，特别适用于各种模型不确定或难以获得解析解的情况下的求解。

本文采用了数值进化算法中的PSO 算法来对氯盐侵蚀环境混凝土结构耐久性评定中的钢筋脱钝模型和保护层锈胀开裂模型进行求解，该算法源于对鸟类捕食行为的研究，利用群体中的个体对信息的共享，使整个群体的运动在问题的求解空间中产生从无序到有序的演化过程，从而获得最优解。

目标函数的最优解则是目标函数取最小值时，对应参数ti、t2与tcr的值。为了获得最优解，可以在目标函数解空间中投放一定数量的“粒子”，粒子i在目标函数解空间中的位置表示为xi，在解空间中的前进速度和方向表示为vi，对于粒子在解空间中的每次移动，即xi的每次取值，都可以通过目标函数获得对应的适应度值，每个粒子在移动过程中会计算自身的适应度值，当前粒子适应度值的绝对值的最小值所对应的解空间位置记为pBest，即为当前粒子的最优位置。此外，所有粒子的pBest所对应的适应度值的绝对值的最小值所对应的解空间位置称为gBest，即gBest是所有pBest中的最优位置。这样就完成了求解问题的抽象，每个粒子的pBest可以看作是同伴的经验，每个粒子根据自己的经验和同伴中最好的经验来决定下一步的移动，从而利用群体智慧完成解空间的寻优任务。

2.2 求解寻优规则

本文所采用的PSO 算法会在解空间中随机的投放一定数量的粒子，即求解问题的随机解，每一轮计算过程中，根据每个粒子的适应度，计算每个粒子在解空间中的最佳位置pBest以及全局最优位置gBest，根据pBest与gBest来指导粒子群在解空间的运动趋势，不断地朝着最优解的位置前进，即数值进化。对于k个粒子而言，找到每个粒子的pBest与全局唯一的gBest后，第i个粒子的运动方式如下所示：

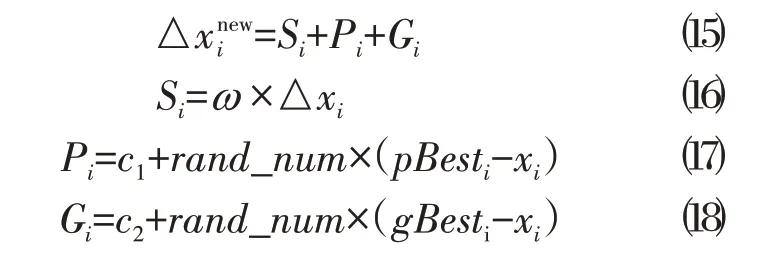
式中：xi为粒子i当前在解空间中的位置；为粒子i在解空间中下一次移动的大小和方向；△xi为粒子i在解空间移动的大小和方向；Si为第i个粒子的记忆项；ω为惯性系数；Pi为第i个粒子的自我认知项；Gi为第i个粒子的群体认知项；c1为局部权重因子；c2为全局权重因子；rand_num为随机数，其值介于（0，1）；pBesti为粒子i的最优位置；gBesti为全局最优位置。

式⒂～⒅中，记忆项Si表示粒子下一次的移动受到上一次移动的影响，自我认知项Pi和群体认知项Gi则体现了个体经验与群体智慧对寻优求解的引导，其中c1和c2则用于调整二者的寻优倾向。ω为惯性系数，该参数控制了记忆项对下一次移动的影响程度，其为动态的非负值，该值的设定方式较为灵活，通常采用线性递减的策略：

式中：Rate为扰动概率；rand0_1为0～1之间的随机数；max_speed为粒子的最大速度；Epoch为总的进化次数；epoch为当前的进化次数。惯性系数ω让PSO 算法在开始阶段让部分粒子拥有较高的运动速度，使得算法有较强的全局寻优能力，随着进化的不断进行，惯性系数逐渐减小，使得求解精度更高，收敛速度更快，即拥有较强的局部寻优能力。

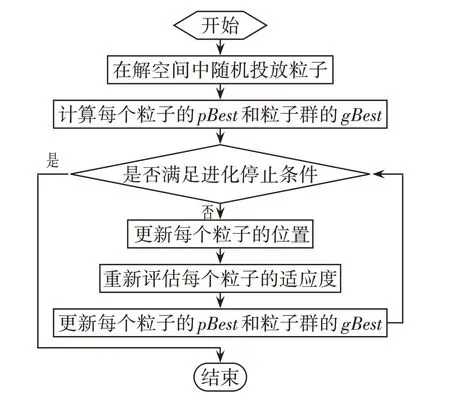
图1 PSO算法流程Fig.1 Chart of PSO Algorithm

本文则通过PSO 算法强大的寻优求解能力，对式⑺与式⒂进行求解，从而实现对钢筋脱钝时间ti和保护层锈胀开裂时间tcr的求解。

3 算法安全性、稳定性、可用性研究

对于PSO 算法而言，不同的解空间模型会影响算法的准确度、求解速度及稳定性。目标函数的解空间存在多极值点会导致算法陷入局部最优，也可能导致求解结果不稳定，使得PSO 算法存在求解风险。因此，在使用PSO 算法之时，要结合实际求解模型，对算法求解的安全性进行评估，在满足安全性的基础上，调整进化算法的参数，进一步对求解的稳定性和可用性进行评估。

3.1 算法安全性评估

PSO 算法的安全性指的是算法陷入局部最优的可能性，PSO 算法陷入局部最优的可能性越大，算法的安全性越低，会导致对模型求解存在多解问题。但如果误差函数是单调的，那么目标函数的解空间必然只有一个极值点，PSO 算法必定不会陷入局部最优解。因此PSO 算法的安全性可以通过误差函数的单调性来进行判断。

社交电商将互动、讨论、分享、沟通、关注等多种社交元素综合运用到电子商务交易的过程。这些社交元素会产生裂变效应，由客户去分裂出新客户，从而产生低成本的客户流量。以拼多多为代表的社交电商平台更是将裂变功能发挥得淋漓尽致。根据QuestMobile研究数据显示，截至2017年12月，拼多多的用户规模仅次于手机淘宝和京东排列第三名。在用户的活跃度方面，拼多多仅次于手机淘宝，已经超过了京东和唯品会。拼多多这种短时间的客户流量爆发，正是得益于微信的社交生态网，借助小程序的嵌入来实现购买链接在网购用户的朋友圈里以及微信群里快速传播从而实现客户的裂变。

当ti≤t1时，对式⑷进行关于自变量ti的求导，可得：

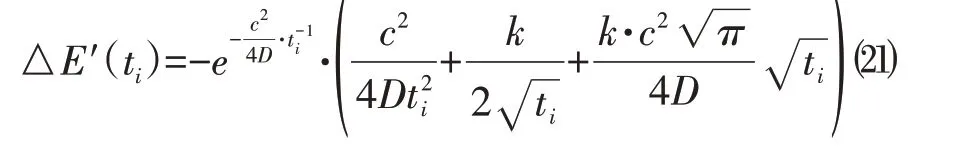
其中k、c、D均为大于0的常数，可证明当ti≤t1时，ti的误差函数为单调递减。

同理可得，当ti＞t1时当对式⑹进行关于自变量t2的求导，可得

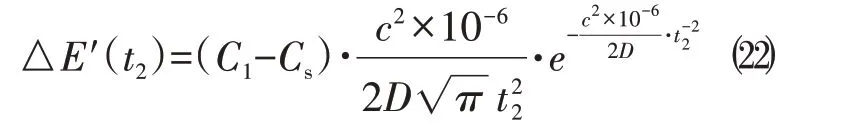
可见，对于式⑹而言，t2在解空间中是单调变化的，单调性取决于C1与Cs的大小。

对于tcr的求解的安全性，可以将式⑾进行关于自变量tcr的求导，可得：

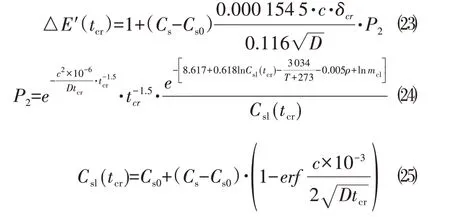
其中保护层厚度c、氯离子扩散系数D、保护层锈胀开裂时间tcr是大于0的值，可得：

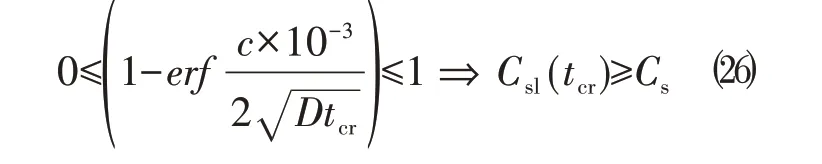
进一步地，P2 恒大于0，因此可得式■23恒大于0，即可证明式⑾为单调递增的函数。

结合上述结论，钢筋脱钝模型与保护层锈胀开裂模型的误差函数均为单调函数，可证明其目标函数有且仅有一个极值点。因此通过PSO 算法对目标函数进行求解是安全的，不存在陷入局部最优解的风险。各模型的目标解空间分布如图2 所示，各模型的输入参数取值如下所示：混凝土表面氯离子聚集系数k=1.571 14 kg/m3，保护层厚度c=0.06 m，钢筋表面温度T=30 ℃，混凝土表面氯离子浓度达到稳定值的时间t1=10 a，钢筋脱钝时间ti=0∶0.1∶200 a，中间变量t2=0∶0.1∶200 a，保护层锈胀开裂时间tcr=0∶0.1∶200 a，氯离子扩散系数D=2.739 25×10-5m2/a，混凝土表面氯离子浓度Cs=5 kg/m3，混凝土制备时氯离子掺入量Cs0=1 kg/m3，t时刻x深度处色氯离子浓度C（x，t）=1 kg/m3，中间变量C1=0.020 601 2 kg/m3，混凝土电阻率ρ=3.68 KΩ/cm，局部环境系数mcl=4.5 null，保护层开裂时钢筋临界锈蚀深度δcr=0.087 6 mm。

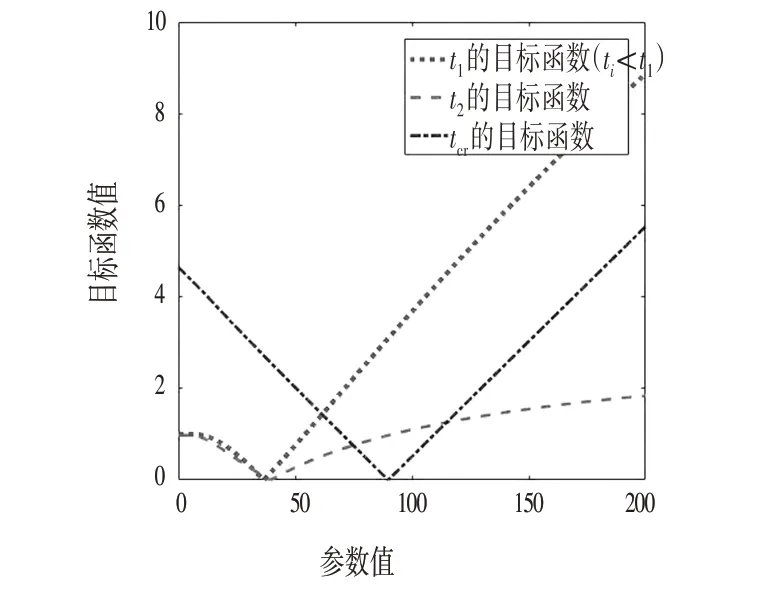
图2 目标函数解空间分布Fig.2 Spatial Distribution of Objective Function Solution

3.2 算法可用性评估

在证明了算法的安全性之后，需要对算法的可用性进行评估，可用性指的是算法的求解速度是否满足够迅速，是否满足使用场景的需求。稳定性与可用性主要受到算法参数与解空间分布的影响，本文所使用的PSO 算法的参数包括：minPos、maxPos为寻优下限、上限；Size为粒子群的粒子个数；c1为粒子局部加速度；c2为粒子全局加速度；Epoch为最大进化次数；Rate为扰动率；max_speed为粒子的最大速度；△E为进化停止条件。

不同的寻优求解问题拥有不同的解空间，在面对不同解空间时，上述各参数对求解结果的影响程度各不相同。针对钢筋脱钝时间ti与保护层锈胀开裂时间tcr的解空间，PSO 算法所采用的基础测试参数如表1所示。

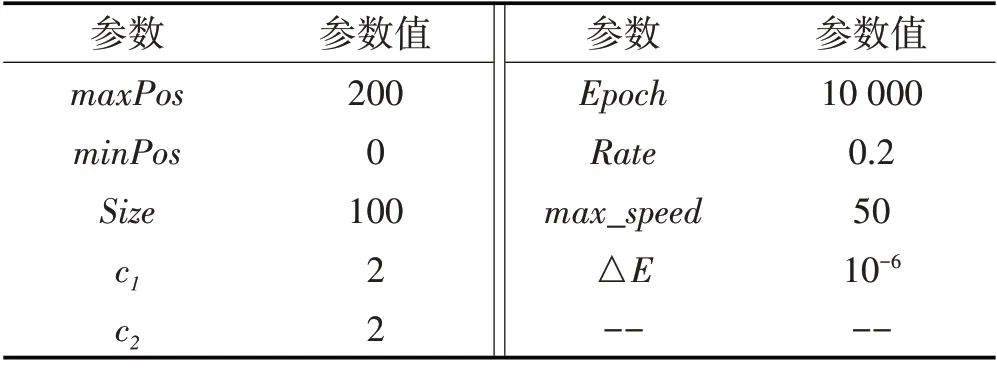
表1 PSO算法参数设置Tab.1 Parameter Setting of PSO Algorithm

在3.1 节中，已证明误差函数均为单调函数，在运算精度要求不高的情况下可采用数值迭代的方式来寻找误差函数接近0 时的参数值，其中数值迭代的最小步进值即是求解的精度，但在求解精度要求较高的情况下，其运算速度是无法接受的。PSO 算法则可以在保证精度的前提下，实现问题的高速求解。本文使用C++对算法进行实现，在Intel I7 9850H 平台进行测试，模型输入采用表1 所示参数，PSO 算法采用表1 所示参数，通过保护层锈胀开裂模型tcr的求解来展示两种算法在求解时间上的差异，结果如表2所示。

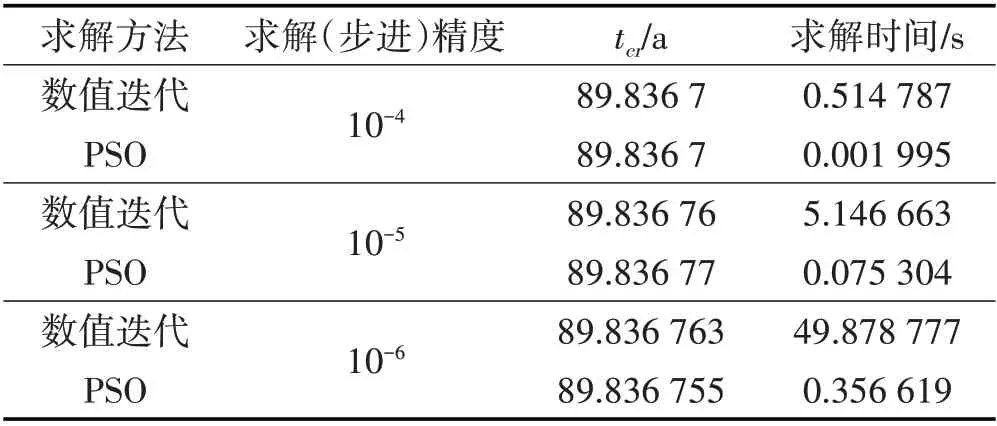
表2 数值迭代算法与PSO算法求解的时间差异Tab.2 Time Difference between Numerical Iterative Algorithm and PSO Algorithm

从表2可知，在不同求解精度的情况下，PSO 算法对模型的求解速度相较于数值迭代算法拥有数量级的优势，在求解精度为10-6的数量级上，PSO 算法的求解时间仅为0.356 619 s，可见PSO 算法对于本文所述的模型求解问题具备极好的可用性。

3.3 算法稳定性评估

PSO 算法的稳定性是指求解结果可以达到的稳定精确度。对于PSO 算法的稳定性，可根据多次模型求解，统计目标函数均值、目标函数方差进行评估。本文在大气区氯盐侵蚀环境下，针对目标函数⑸、⑺、⒁，采用表1 与表2 的参数进行100 次重复求解，目标函数求解结果如图3～图5 所示。统计了误差函数与目标函数的均值与方差，如表3所示。从表3可知，在表2 设置的参数下，PSO 算法对误差函数的求解均达到了进化停止条件，误差函数均值达到了10-7的数量级，求运算方差极小，达到了10-11的数量级。图3～图5 可知，PSO 算法的求解结果仅在10-4数量级上存在较小的波动，能够保证在10-3数量级，即可以对钢筋脱钝时间ti与保护层锈胀开裂时间tcr实现精确到“小时”级的预测。综上所述，PSO 算法对钢筋脱钝模型与保护层锈胀开裂模型求解可达到10-3级别的稳定性，其求解精度满足科研与工程要求。

图3 PSO算法对ti的求解结果Fig.3 The Result of PSO Algorithm for ti

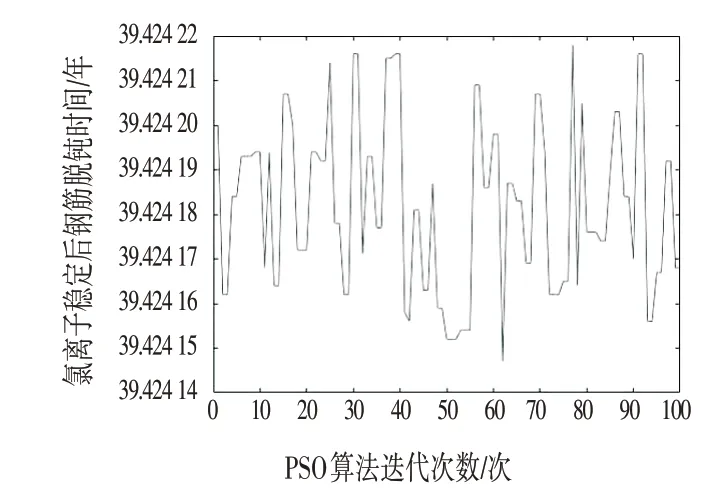
图4 PSO算法对t2的求解结果Fig.4 The Result of PSO Algorithm for t2

图5 PSO算法对tcr的求解结果Fig.5 The Result of PSO Algorithm for tcr

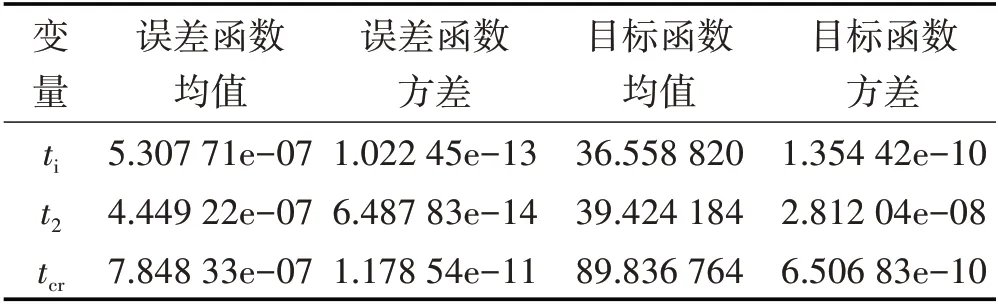
表3 粒子加速度对求解的影响Tab.3 Time Difference between Numerical Iterative Algorithm and PSO Algorithm

4 结论

本文针对PSO 算法在氯盐侵蚀环境混凝土结构耐久性评定中的应用展开研究，通过PSO 算法来对耐久性评定中难以获得解析解的钢筋脱钝时间与保护层锈胀开裂时间模型进行求解，并通过稳定性、安全性和可用性三个维度对PSO 算法求解上述模型的结果进行评估和论证，对于氯盐侵蚀环境混凝土结构耐久性评定中的模型求解，满足求解的安全性，实现了“小时”级别的求解精度和快速的求解速度，满足科研与工程应用的需求。