基于粗定位-精匹配的双目视觉目标定位方法
2021-11-03杜玉晓郑晓森陈祎杭王小桥王公东钟楠
杜玉晓 郑晓森 陈祎杭 王小桥 王公东 钟楠
基于粗定位-精匹配的双目视觉目标定位方法
杜玉晓1郑晓森1陈祎杭1王小桥2王公东2钟楠2
(1.广东工业大学自动化学院,广东 广州 510006 2.广东海信电子有限公司,广东 江门 529000)
为提高双目视觉系统定位精度,提出一种基于粗定位-精匹配的双目视觉目标定位方法。利用Canny边缘检测算法对左、右图像中的目标物体进行识别,提取目标物体最大、最小矩形区域,从而实现目标物体的粗定位。采用SIFT算法得到左、右图像中目标的特征点;用RANSAC得到精确匹配点,并计算出左、右图像中物体之间的透视变换关系;根据透视变换关系确定左图像的目标特征点在右图像目标潜在匹配点的位置,得到目标物体的三维位姿及质心坐标,从而实现目标物体的精匹配。实验结果表明:本文方法平均测距误差为4.6 mm,平均耗时为1.265 s,相比SIFT、SURF特征匹配定位方法,具有定位精度高、运行时间短的特点。
双目立体视觉;粗定位;精匹配;SIFT算法;RANSAC;透视变换
0 引言
随着机器人自主化的不断深入,对机器视觉技术的要求也不断提高。以往机器视觉主要通过像素灰度和梯度获取图像信息,但三维图像信息更为丰富。双目立体视觉技术通过模拟人类的视觉结构,获取物体不同角度的图像,利用投影点之间的视差恢复物体的空间坐标,实现目标三维空间位置的测量。该技术主要基于三角测量原理,为非接触式测量,具有成本低、结构简单、效率高等特点,广泛应用于机器人导航、机器人工业生产、农业采摘及三维场景感知等场合,实现机器人在未知环境中快速、准确地识别目标物体信息,规划可行路径,完成基于视觉的任务。目前,双目立体视觉技术已成为自主机器人技术的关键组成部分[1-2]。
双目立体视觉技术的核心是双目视觉定位的精度,正确获取目标的位置、位姿,关键在于选取立体空间位置一致的左、右图像中的同名特征点,即立体匹配。立体匹配方式主要分为基于全局的立体匹配、基于局部的立体匹配和基于特征的立体匹配。本文采用基于特征的立体匹配,通过提取左、右图像的局部特征点进行匹配来实现目标定位,如Harris角点、尺度不变特征变换(scale invariant feature transform, SIFT)、快速鲁棒性特征(speed up robust feature, SURF)、加速分割测试特征(features from accelerated segment test, FAST)等。其中,SIFT因对尺度、旋转、光照等变化有良好的鲁棒性而广泛应用[3],但其计算复杂度较高,实时性差。SURF在保证匹配率的基础上,改善了SIFT算法实时性差的问题[4]。在SIFT和SURF算法基础上,学者不断进行改进,以期通过提高特征匹配率和缩短匹配时间来提升双目视觉定位系统的定位精度和实时性[5-9]。但上述特征提取方法存在2个问题:1)提取目标多个特征点,导致立体匹配计算量大、实时性差;2)无法得到精确、连续的视差图,且在最后定位时,大多只能以多个特征点的均值作为定位点,并非目标中心点;只能获取目标在摄像头坐标系下的深度距离(轴方向),无法精确获取目标的水平距离(轴方向)和垂直距离(轴方向)。
为解决上述问题,本文提出一种基于粗定位-精匹配的双目视觉目标定位方法。在粗定位阶段,快速获取目标区域,并分析目标区域的中心点及关键角点信息;在精匹配阶段,在目标区域内提取精确的匹配点并拟合出左、右目标区域的透视变换关系;最后通过相似三角形原理,还原目标的位置信息。
1 双目视觉系统
在双目视觉系统中,通常使用水平左、右摄像机从不同角度获取目标图像,并利用视差原理重建目标的三维信息[10-14]。平行双目视觉测距模型如图1所示。
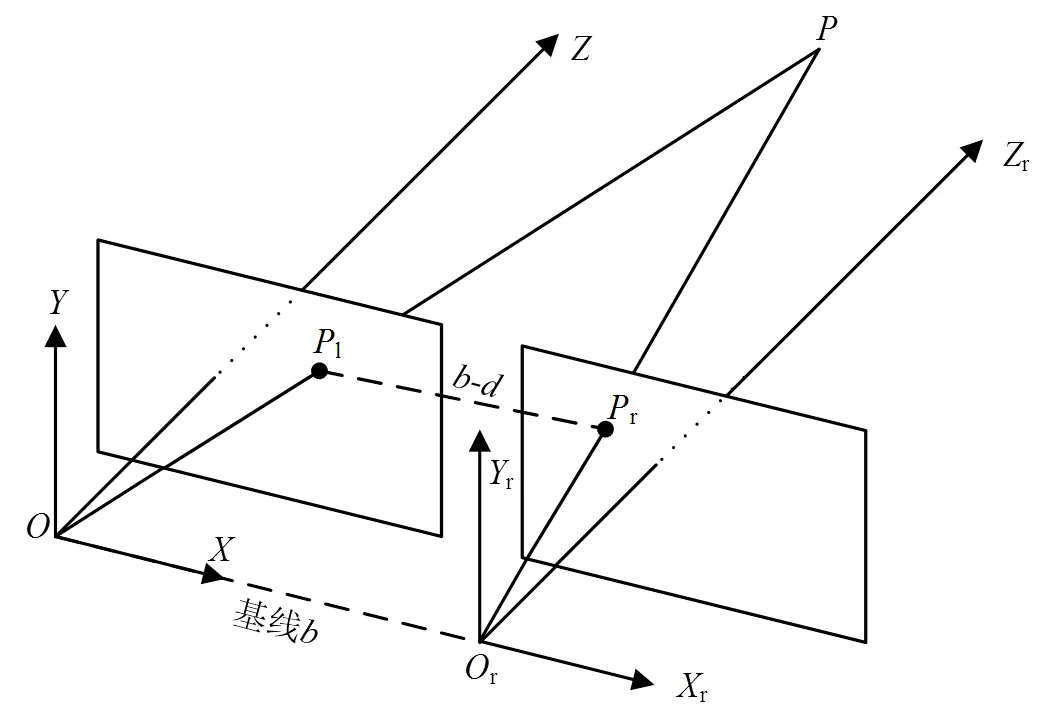
图1 平行双目视觉测距模型

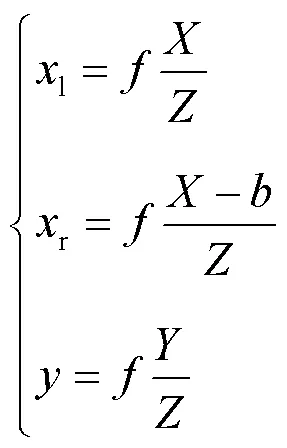
式中为摄像机的物理焦距。
由此可得目标物体在主摄像机(左摄像机)坐标系中的坐标为
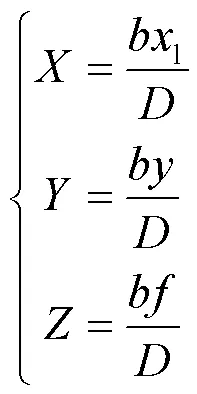
因此,只要能找到左、右2个摄像机图像中的任意一点的相应匹配特征点,就可以计算出该点的实际三维坐标,从而还原三维场景。
1.1 摄像机标定与校准
要近似达到理想的平行双目摄像模型的关键在于摄像机的标定与校准。标定摄像机的内外参数[15-16]包括图像中心坐标、左、右摄像机焦距、旋转矩阵、平移向量等。标定系统主要涉及4个坐标系:世界坐标系、摄像机坐标系、图像坐标系和像素坐标系。在不同坐标系下,物体坐标都不一样,但各个坐标系之间能通过摄像机外部参数旋转矩阵和平移向量来实现相互之间的转变,其相互关系如图2所示。
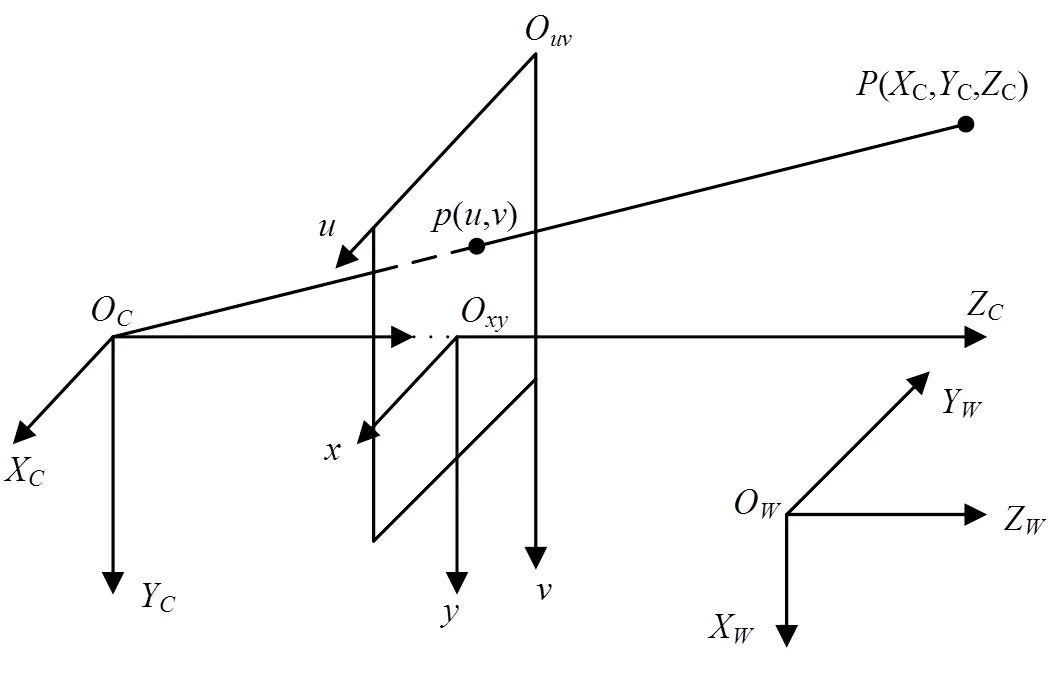
图2 坐标系的变换关系
像素坐标系与图像坐标系之间的变换关系为
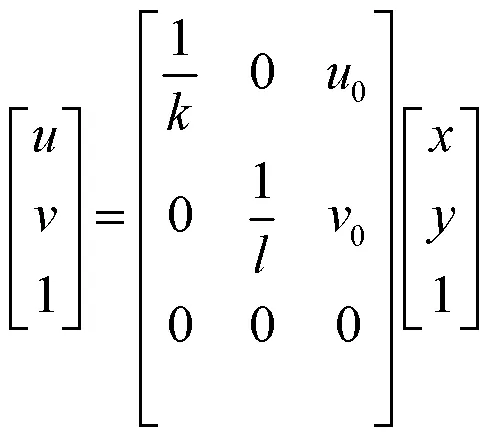
式中×(单位mm)为像素点的物理大小。
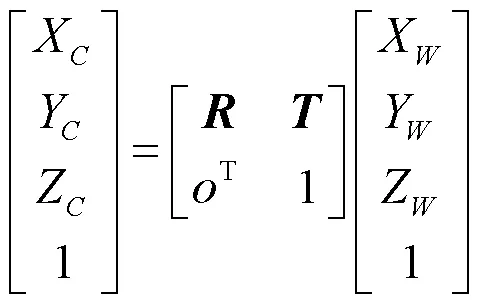
摄像机获取的空间任意点,通过坐标系间相互转换即可得出点在世界坐标系下的坐标为
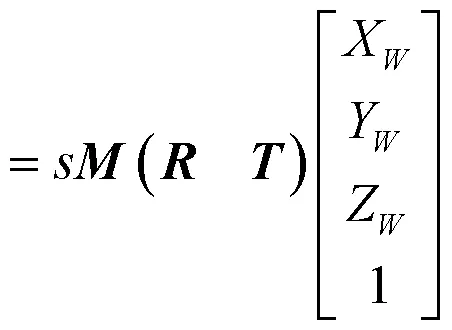
1.2 极线约束
常用的匹配约束条件有极线约束、连续性约束、相似性约束、唯一性约束和顺序一致性约束[17]。其中极线是较为可靠、有效的几何约束条件,因此本文采用极线约束。
空间中的任意一点,通过双目视觉系统左、右摄像机捕获图像,分别在左、右立体图像上有1个对应点。根据射影几何原理,三维空间中同一点的2个对应点存在极线约束关系——左(右)图中的投影点在右(左)图中对应点位置一定被约束在一条直线上,这条线被称作为极线[18]。将三维空间中的点(,,)投影至2个重合平面l、r,分别交于点1、2。由此点、1、2所构成的平面与2个投影平面分别相交于极线1、2,如图3所示。
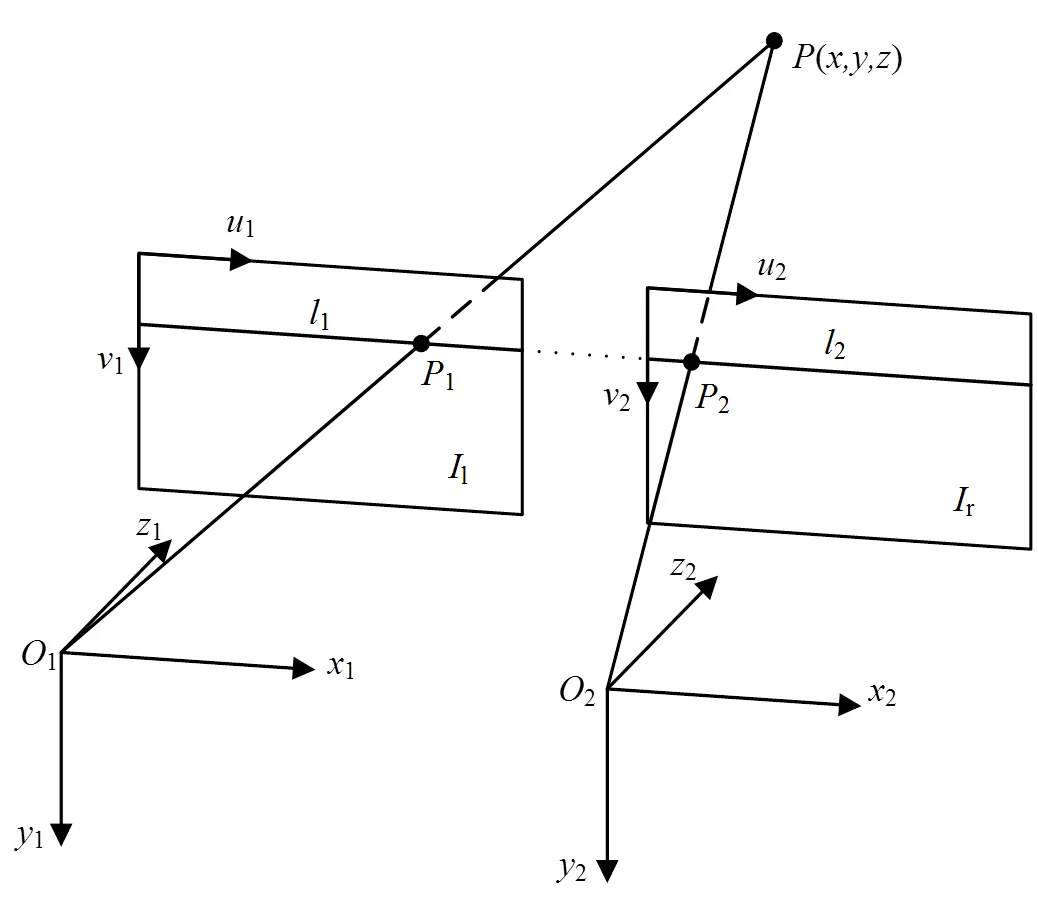
图3 双目立体匹配模型
2 目标定位系统
本文定位算法框架结构如图4所示。从优化搜索策略出发,本文采用Canny边缘检测算法对目标区域进行粗定位,以避免不必要的特征提取和匹配的庞大计算量,具有较好的实时性和鲁棒性,并通过边缘轮廓获取质点。精匹配阶段,在目标区域提取SIFT,并通过随机抽样一致性算法(random sample consensus,RANSAC)获取优质的匹配结果,建立左右区域的透视变换关系,从而利用平行双目视觉模型恢复目标物体的三维重构及计算目标物体质心的三维坐标位置。这样既具有粗定位快速的特点,又有精匹配结果较高一致性的特点。
2.1 粗定位
在粗定位阶段,左、右图像采用Canny边缘检测算法进行目标识别,提取目标物体轮廓并得到左、右目标中心点,用于下一阶段的像素搜索范围的压缩。
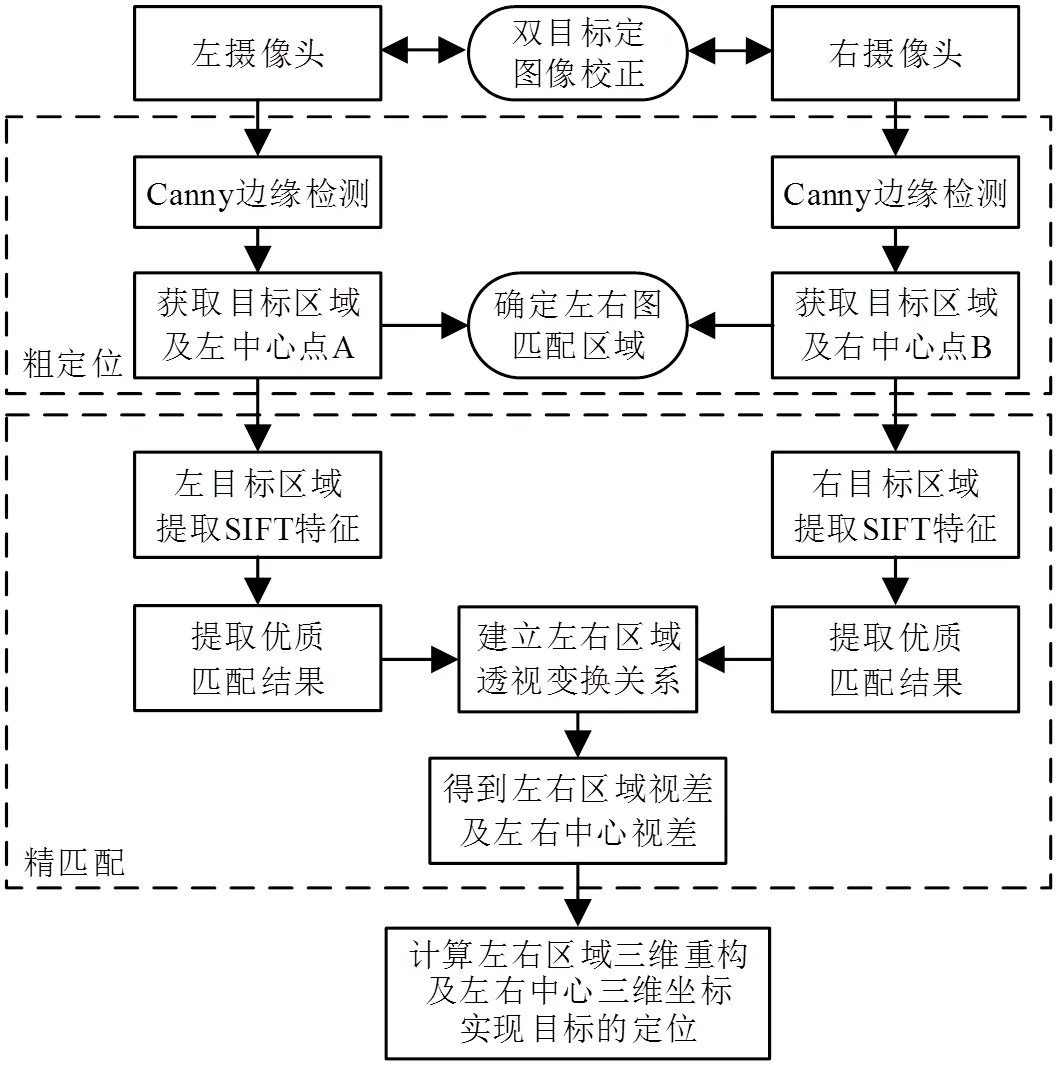
图4 定位算法框架
Canny边缘检测算法具有效果好、误码率低、精度高等特点,得到的边缘宽度是单个像素宽度。首先,用3×3的高斯平滑滤波器对图像进行卷积,等效于降采样,得到图像(,);然后,计算图像(,)像素点的梯度和方向,图像梯度计算可转化成像素灰度变化,计算公式为

对图像像素邻域4个方向(−45°, 0°, 45°, 90°)进行非极大值抑制,即中心像素点与邻域上4个方向的像素点进行幅值比较,若最大,保留;否则舍去。对梯度图像采用双阈值方法检测并接连边缘,分别选取2个阈值1和2(1<2),若像素点的梯度值>2,则此像素点为边缘特征点;若像素点梯度值<1,则此像素为非特征点;当2>梯度值>1,则需判断此中心点8邻域点中,是否有满足梯度值>2的点,若有,则该像素点也为边缘特征点。
通过立体校正的双目平行摄像机,在极线约束下,左、右图像的特征匹配点在同一水平线上(即纵坐标相等),因此匹配搜索范围降到一维。但考虑校正后左、右图像仍可能存在像素误差,匹配初始像素
2.2 精匹配
精匹配完整地建立了左、右区域的精确关系。
SIFT算法基本原理是对二维图像构建尺度空间,分析每层图像的局部特征并找到极值点,排除易受干扰点和低对比度的极值点;再使用该点邻域内的信息来描述特征点信息;从而得到具有旋转、光照和尺度不变性的特征点[19]。
SIFT算法主要有5个步骤[20]:
1)构建尺度空间;
2)尺度空间局部极值检测;
3)排除易受干扰极值点;
4)确定每个特征点方向;
5)特征点描述子生成。
一般特征点描述计算4×4窗口中8个方向的梯度信息,共有128维方向信息,运算量较大,运算时间长,无法达到实时性要求。此时若直接用透视变换求取关系矩阵代价过高,且粗匹配存在大量误匹配点,使后续结果误差较大。于是引入RANSAC假设数据内群来计算合适的内群模型。RANSAC可从一组包含“局外点”的观测数据集中,通过迭代方式估计数学模型的参数[21]。当有效数据占绝大多数时,可通过最小二乘法来拟合参数和误差。
3 实验结果及分析
实验平台采用Intel Core i7-7700HQ @2.80 GHz的PC机,在VS2017上用C++与OpenCV进行调试。图像采集使用HBV-1780平行双目摄像机,视场角、焦距为72°/3.6 mm,图像分辨率为640×480像素。
3.1 双目标定结果
在目标定位前,需要对双目摄像机进行标定,包括左、右摄像机内参和外参(2个摄像机的相对位置关系)。本文采用张正友棋盘标定法进行标定。实验采集标定板左、右图像14组,提取棋盘点进行标定,得到摄像机参数如表1所示。

表1 摄像机标定参数
3.2 粗定位目标识别
把左摄像机作为参考坐标系来描述空间信息,采用粗定位方法实现目标的粗定位,左、右图像目标识别结果如图5所示。利用粗定位方法分别找到左、右图像目标的边缘,绘制最小外接轮廓、最大外接轮廓及中心位置,提取目标区域位置,并保留相关信息供后续使用。粗定位目标识别平均执行时间为396 ms。

图5 粗定位目标识别结果
3.3 精匹配
在粗定位基础上,左、右区域分别提取SIFT特征点,单纯通过SIFT算法确定2个图像的透视变换关系过程比较复杂且结果不尽人意,如图6所示。采用RANSAC找到优质的匹配点,从初匹配的105对匹配点中选取30对匹配准确的匹配点组,如图7所示,此过程耗时669 ms。

图6 SIFT特征点匹配结果

图7 RANSAC精确匹配结果
通过透视变换找到左、右摄像机成像区域的对应关系。透视变换是将图像投影到新的视平面,通过透视变换找到一个3×3的投影矩阵来描述左、右区域的关系,从而可通过矩阵找到左图像素点对应特征点在右图中的位置,并快速地还原出图像位置。透视变换公式为
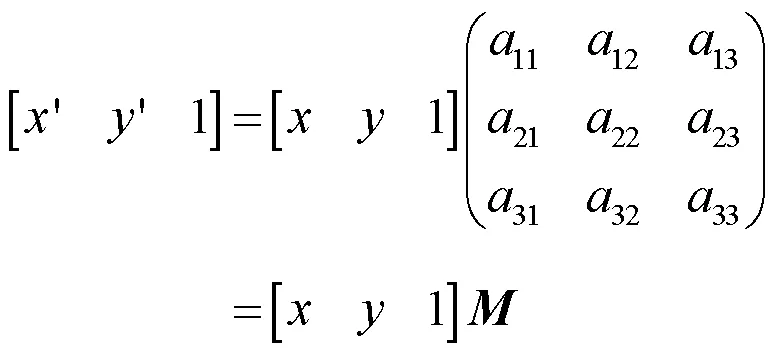
通过精确的匹配点得到透视变换矩阵,从而可求右图对应像素点位置;再通过透视变换,用SURF提取特征,并使用KNN进行匹配,可得到113对精确的匹配点对,如图8所示。

图8 透视变换后精确的匹配点
3.4 定位结果及分析
根据左、右区域的透视变换关系,可求视差图,如图9所示,三维重构图如图10所示。

图9 视差图
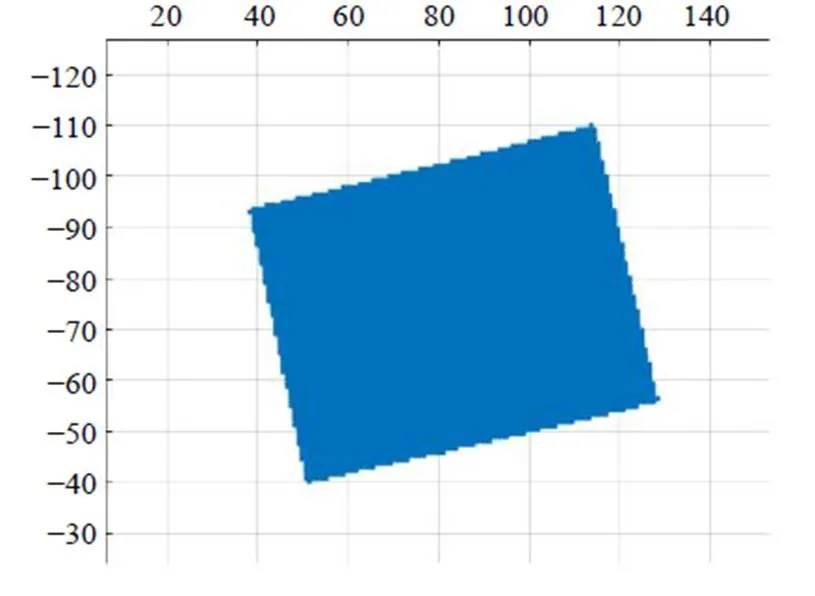
图10 三维重构图
由于深度与视差成反比,当视差很小时,即使其发生非常小的变化,都会使深度发生很大变化;同样当深度很大,深度变化不明显时,视差基本不会变化,因此视差变化不明显。这和前面的理论相吻合,所得视差也可以求出目标的深度信息。
通过边缘检测提取的最小轮廓(4个角点)及质点,并通过透视变换关系计算它们在三维空间的坐标,实测数据如表2所示,实测坐标-截面结果图如图11所示。本文算法求取目标位置和实际测量误差在7 mm以内,平均误差为0.676%。
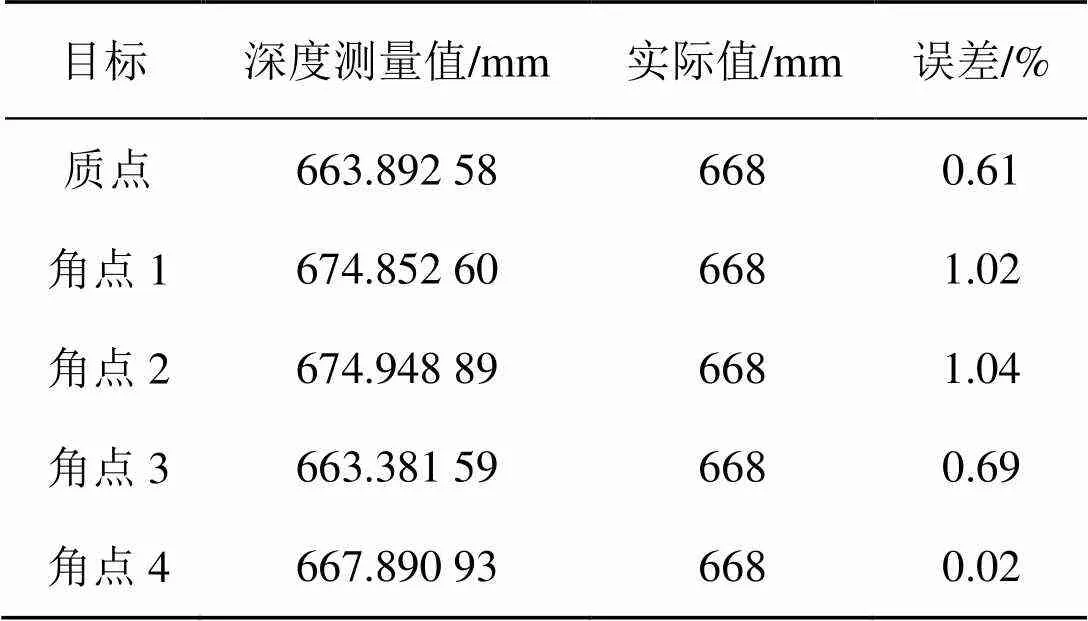
表2 实测深度数据与实际值对比
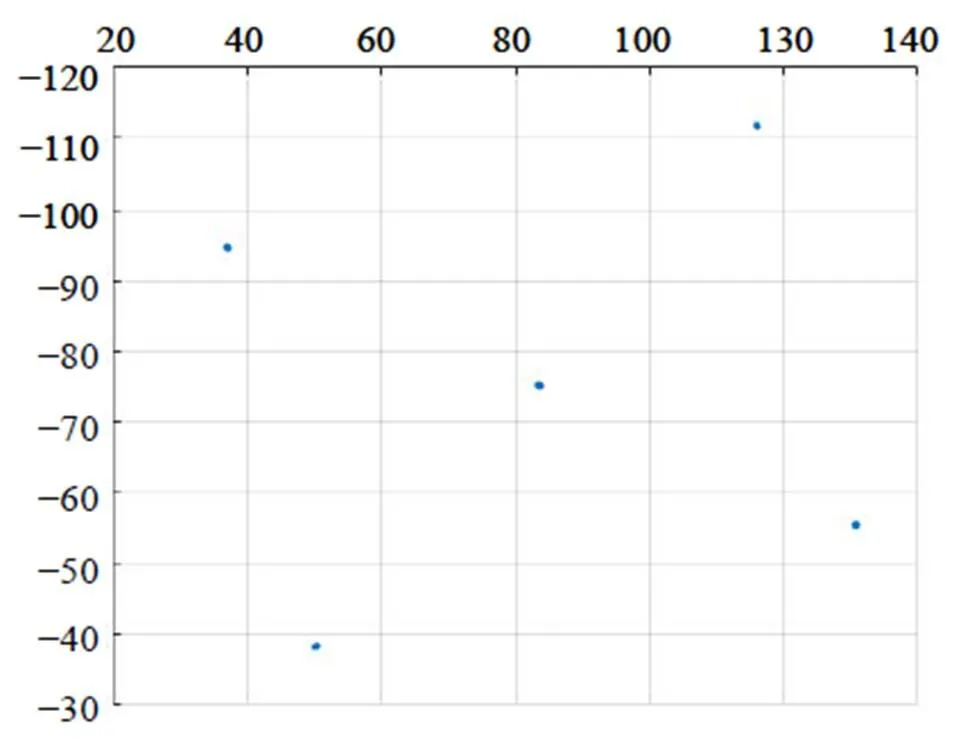
图11 实测坐标X-Y截面结果图
本文方法分别与基于SIFT、SURF特征匹配定位方法进行比较。在定位精度方面,各方法平均测距误差依次为:4.6 mm、12.6 mm、13.6 mm。由此可知,本文方法测距精度有明显优势。在实时性方面,各方法平均耗时分别为:1.265 s、5.801 s、3.526 s。本文方法候选匹配点数量减少,耗时也相应减少,同时精匹配过程误匹配的概率也减少。
4 结语
本文提出基于粗定位-精匹配的双目视觉定位方法,在粗定位阶段采用Canny边缘检测获取目标区域和目标质心。在精匹配阶段,以目标区域为搜索范围,求出左右区域的透视变换关系,最后利用匹配结果恢复目标的位置及质点空间坐标,实现了目标的精确定位。该方法用于双目立体视觉,定位误差较小且定位实时性高,在一定的范围内可以实现目标精确快速定位,具有一定的应用价值。
[1] 杜娟,邱海涛.基于共享坐标系的双目立体匹配算法实现[J].自动化与信息工程,2020,41(5):7-11.
[2] 王浩,马振书,穆希辉,等.危险品弹药遥操作搬运机器人的研究与开发[J].科学技术与工程,2007,7(3):393-395,405.
[3] 肖健.SIFT特征匹配算法研究与改进[D].重庆:重庆大学, 2012.
[4] 韩峰,李晓斌.基于改进SURF算法的双目视觉定位[J].电视技术,2015,39(23):22-25,30.
[5] 李耀云,贾敏智.基于Harris-SIFT算法的双目立体视觉定位[J].电视技术,2013,37(9):23-25,29.
[6] 朱镕杰,朱颖汇,王玲,等.基于尺度不变特征转换算法的棉花双目视觉定位技术[J].农业工程学报,2016,32(6):182-188.
[7] 韩峰,韩文静.一种改进SURF算法的视觉定位[J].电光与控制,2016,23(7):29-33.
[8] 程佳兵,邹湘军,陈明猷,等.多类复杂水果目标的通用三维感知框架[J].自动化与信息工程,2021,42(3):15-20.
[9] 惠记庄,罗丽,杨永奎,等.基于SURF-BRISK的目标识别匹配与定位方法研究[J].长安大学学报(自然科学版),2016, 36(3):93-101.
[10] 罗桂娥.双目立体视觉深度感知与三维重建若干问题研究[D].长沙:中南大学,2012.
[11] 李先祥,陈思琪,肖红军,等.基于SGBM算法与BM算法的三维重建分析[J].自动化与信息工程,2019,40(5):6-12.
[12] 徐昱琳,杨永焕,李昕,等.基于双目视觉的服务机器人仿人机械臂控制[J].上海大学学报(自然科学版),2012,18(5): 506-512.
[13] ZHAO Peng, NI Guoqiang. Simultaneous perimeter measure- ment for 3D object with a binocular stereo vision measure- ment system[J]. Optics & Lasers in Engineering, 2010,48(4): 505-511.
[14] 项荣,应义斌,蒋焕煜,等.基于双目立体视觉的番茄定位[J].农业工程学报,2012,28(5):161-167.
[15] ZHAO Z J, LIU Y C, ZHANG Z Y. Camera calibration with three noncollinear points under special motions[J]. IEEE Transactions on Image Processing, 2008,7(12):2393-2402.
[16] 蓝福明,杨宜民.基于OpenCV和本质矩阵的双目立体视觉摄像机标定方法[J].自动化与信息工程,2012,33(6):4-7.
[17] 时洪光,张凤生,郑春兰.基于图像校正与灰度相关性的立体匹配算法研究[J].机械,2010,37(8):15-17,33.
[18] 王敏行.一种双目视觉的精准立体匹配算法[J].科学技术创新,2019(13):7-9.
[19] LOWE D G. Distinctive image feature from scale-invariant key point [J].Computer Vision, 2004,60(2):91-110.
[20] 卢洪军.基于双目视觉移动机器人目标的检测与定位[D].沈阳:沈阳工业大学,2017.
[21] 梁远芳,林苗婷,葛坤,等.基于改进的SIFT特征的数字图像无缝拼接技术[J].福建电脑,2014,30(6):9-12,18.
Binocular Vision Target Location Method Based on Coarse Location and Fine Matching
Du Yuxiao1Zheng Xiaosen1Chen Yihang1Wang Xiaoqiao2Wang Gongdong2Zhong Nan2
(1.College of Automation, Guangdong University of Technology, Guangzhou 510006, China 2.Hisense Electronics Co., Ltd. Jiangmen 529000, China)
In order to improve the localization accuracy of binocular vision system, a binocular vision target localization method based on coarse localization fine matching is proposed. Canny edge detection algorithm is used to recognize the target object in the left and right images, and the maximum and minimum rectangular regions of the target object are extracted, so as to realize the rough positioning of the target object. SIFT algorithm is used to obtain the feature points of the target in the left and right images; The exact matching points are obtained by RANSAC, and the perspective transformation relationship between the objects in the left and right images is calculated; According to the perspective transformation relationship, the position of the target feature point of the left image at the potential matching point of the target in the right image is determined, and the three-dimensional pose and centroid coordinates of the target object are obtained, so as to realize the fine matching of the target object. The experimental results show that the average ranging error of this method is 4.6 mm and the average time is 1.265 s. Compared with sift and surf feature matching positioning methods, this method has the characteristics of high positioning accuracy and short running time.
binocular stereo vision; coarse location; fine matching; SIFT algorithm; RANSAC; perspective transformation
杜玉晓,男,1973年生,工学博士,副教授,主要研究方向:自动化装备与集成技术、生物电信号检测及处理技术。E-mail: yuxiaodu@gdut.edu.cn
郑晓森(通信作者),男,1993年生,硕士研究生,主要研究方向:双目视觉,图像处理等。E-mail: 362389141@qq.com
陈祎杭,男,1997年生,硕士研究生,主要研究方向:工业机器人、智能制造。
王小桥,男,1979年生,大专,主要研究方向:工业机器人与视觉测量技术。
王公东,男,1979年生,大专,主要研究方向:工业机器人与视觉测量技术。
钟楠,男,1998年生,工学学士,主要研究方向:工业机器人与视觉测量技术。
TP391.41
A
1674-2605(2021)05-0002-07
10.3969/j.issn.1674-2605.2021.05.002
