基于仿生江豚鱼群共融型装置的设计与实现
2021-11-03孔祥洪黄小双刘帆李炳麟王静峰刘必林陈新军
孔祥洪,黄小双,刘帆,李炳麟,王静峰,刘必林 ,4,5,陈新军,4,5
(1 上海海洋大学海洋科学学院,上海 201306;2 国家远洋渔业工程技术研究中心,上海 201306;3 上海海洋大学工程学院,上海 201306;4 大洋渔业资源可持续开发教育部重点实验室,上海 201306;5 农业农村部大洋渔业开发重点实验室,上海 201306)
中国作为渔业生产大国,随着水产资源在国民经济中的地位逐步凸显,各领域新兴科技与智能设备的应用发展,智能化、集约化、自动化、现代化渔业装备的需求越来越多[1-5]。为了降低养殖成本、减小劳动强度,提高池塘等人工养殖的效率,新兴移动式智能投饲装备的相关研究逐渐成为热点[6-9]。挪威、瑞典、日本、美国等国家在渔业自动化投饲装备上处于研究前列,在降低养殖成本、提高生产效率、提高水产品质量,提高饲料利用率等方面取得了较为显著的成果[10]。日本NITTO SEIKO公司[11]研制的小型料仓投饲系统,通过每个小型养殖塘上方的网箱进行实时监测与远程投饲。挪威Storvik公司[12-13]自动投饲系统中,以行车为基础架构,利用移动物流车机器人进行电力滑车完成每个池塘的移动式投饲。国外自动投饲系统大多适用于工业化水产养殖,该养殖模式存在建设周期长、建设成本大、工业生产要求高等问题,在科技兴农的推广中存在一定难度,因此使用小型的移动式投饲装备可行性更高。目前国内的自动投饲装备主要为岸基抛撒式和船载抛投式[13],岸基抛撒式存在投放范围固定、易造成部分水体污染等问题;船载式移动投饲弥补了岸基投饲的不足,但船活动范围有限,不能航行于水草等复杂环境,且螺旋桨推进方式鱼群惊扰大,环境共融性不足。
鲨鱼、海豚等水生动物的高效游动机理已成为研究热点[14]。特别是鲸目类的海豚因具有良好的减阻机制、极高的爆发加速度、较高的游动速度,还能完成跃水、空中转体、滚翻、大曲率转向、乘浪等高难度动作,成为仿生机器鱼领域的重要研究对象[14-16]。仿生机器鱼环境共融性的优势[17-18],对渔业生产具有重要的意义与研究价值。由于机器仿生鱼推进效率、推进方式等直接影响其水下负载力,受当前机器鱼仿生推进方式的限制,目前主要研究热点与应用方向主要集中于水产养殖智能监测等[19]方面,在移动投饲等方面的应用仍有不足。作为背腹式游动的水生生物,海豚游动需氧量较大,其游动轨迹呈波浪形以获得更多氧含量,将其作为水产养殖业智能装备具有一定优势[15-18]。
本研究主要探究豚体高效推进游动机制,构建生物推进运动方程,设计开发仿生江豚机器鱼,具备推进效率高、环境共融性强等优势,实现池塘智能化移动投饲,解决传统螺旋桨在养殖环境中对鱼群的惊扰与环境共融性不足等问题,以研究一种鱼群共融、能耗低的移动投饲设备与智能监测设备,进而提升水产业养殖现代化、监测智能化程度。同时,弥补仿生鱼与鱼群共融性试验相关研究的欠缺,为鱼类行为学机理与仿生机理探究提供参考。
1 仿生机器鱼分析与设计
1.1 豚体几何模型建立
在仿生海豚外轮廓建模过程中,需要对生物形态进行轮廓提取,鲸豚类生物样本较难获取,以相关研究[20]中的图像为依据,进行豚体正视图与俯视图外轮廓拟合。图1所示,为无喙鼠海豚生物图像作为轮廓拟合曲线[21]。以豚体最前端为原点建立鱼体坐标系O-xyz,研究中忽略背鳍对其生物形态与运动学模型的影响,对轮廓曲线平滑处理。
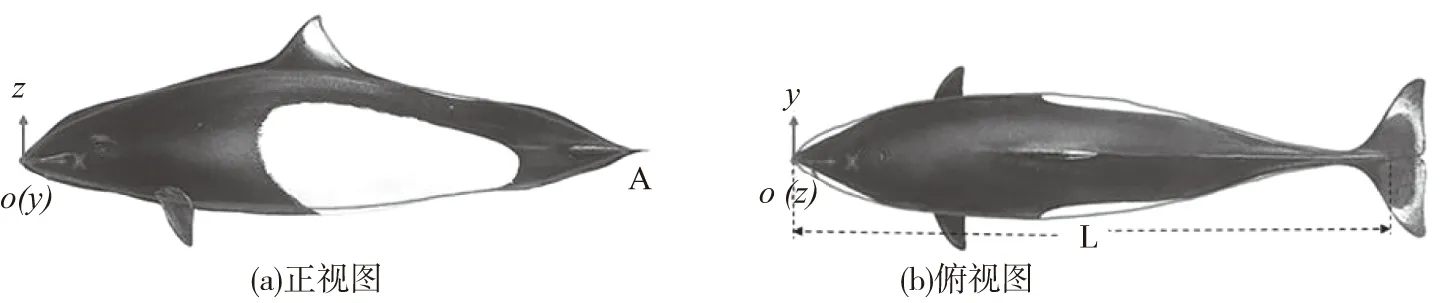
图1 鼠海豚生物图像与轮廓拟合曲线Fig.1 Porpoise bio-images with contour fitting curves
设定静止状态的豚体长度(即豚体最前端至尾椎骨末端长度)L为1,形态轮廓经最小二乘法拟合后,拟合方程的外轮廓拟合优度R2均大于0.99,正视图轮廓拟合方程组O1(x)和俯视图轮廓拟合方程组O2(x)分别为:
(1)
(2)
基于NACA(美国国家航空咨询委员会)翼型方程[22],对豚体外轮廓曲线进行优化,对O1(x)与O2(x)与NACA翼型方程进行回归分析,分别比较O1(x)、O2(x)与NACA翼型方程残差平方和SSE1、SSE2,由于豚体正视图外轮廓为非对称曲线,采用NACA四位数族非对称翼型[22],俯视图采用NACA四位数族对称翼型[23]。
表1为轮廓方程与翼型方程的回归残差平方和。上述两种NACA翼型模型与描边像素点的拟合优度R2均大于0.9,因此选择NACA2421和NACA0018翼型方程分别作为静止状态的豚体正视图轮廓方程C1(x)和俯视图轮廓方程C2(x)[24],即对于海豚正视图,轮廓方程为非对称四位数翼型NACA2421[22],即NACA2421翼型方程中参数分别为c=1,m=0.02,p=0.4,t=0.21;对于海豚俯视图,轮廓方程为对称四位数翼型NACA0018[22],即NACA2421翼型方程中参数分别为c=1,t=0.18。其中,m—翼型最大弯度与翼型弦长的比值;p—翼型最大弯度处的位置;c—翼型弦长;t—翼型最大厚度。
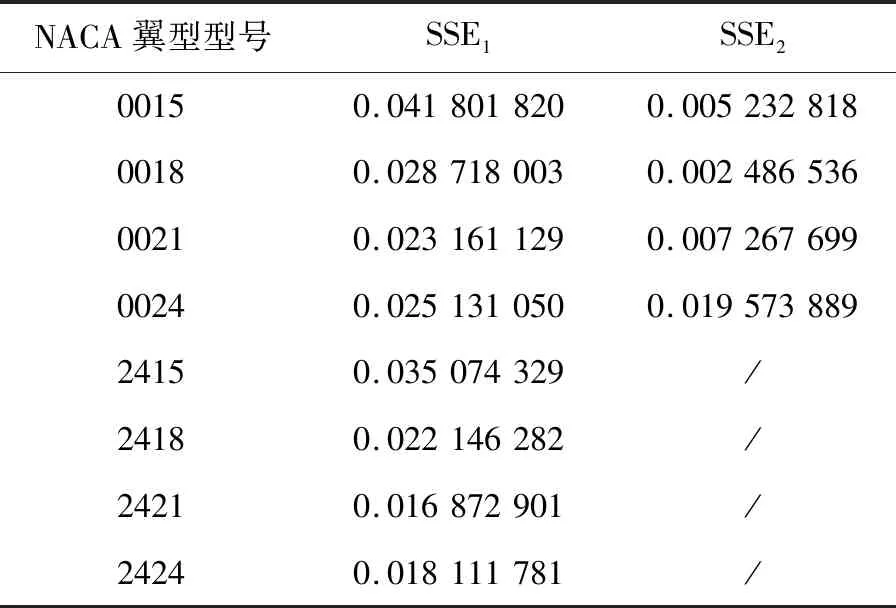
表1 轮廓方程与翼型方程的回归残差平方和Tab.1 Residual Sum of Squares between outlines equations and airfoil equations
1.2 鱼体运动学模型
相关研究[25-26]表明,鱼体波动是影响机器鱼共融性等仿生程度的重要因素,也是提高仿生性与机动性的重要指标之一,因此为提高移动投料平台的环境共融性,建立鲸豚类背腹式推进鱼体运动学模型。根据Lighthill理论[27],研究鱼体体干线波动情况,豚体体干线的摆动沿x方向逐步增大,其鱼体x位置处摆动的振幅方程为:
A(x)=p0+p1ep2x
(3)
式中:A(x)—鱼体x位置处摆动的振幅;p0、p1、p2—振幅方程系数。
豚体体干线的波动方程为:
(4)
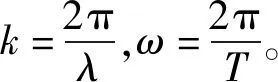
豚体体干线的运动方程为:
F(x,n)=A(x)D(x,n)
(5)
图2为以体长L为单位的摆动角直角坐标系示意图。

图2 摆动角直角坐标系示意图Fig.2 Illustration of the rectangular coordinate system of the wiggle angle defined
定义摆动角θ为o′A与x′轴的夹角。摆动角θ进行如下规定:静止状态的豚体摆动角θ0=0°;摆动角θ的正负表征豚体摆动方向,规定尾椎骨末端中心点A点向z′轴正半轴弯曲时,摆动角θ为正值,反之,摆动角θ为负值;摆动角θ的大小可表征豚体摆动振幅大小。
某一运动时刻n的摆动角为:
θ(n)=θmaxD(x,n)
(6)
最大摆动角为:
(7)
式中:Amax为最大振幅,l为A点至O′点的水平距离。
根据视频资料与相关研究[28],发现海豚尾椎骨末端上下摆动的幅度为体长L的7.8% ~ 20%[14,21],因此表2所示为豚体运动模型参数。
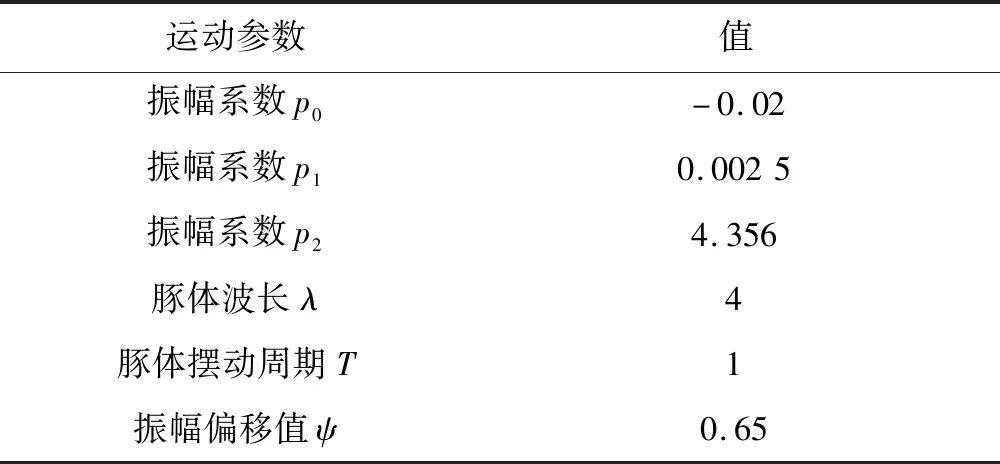
表2 豚体运动模型参数Tab.2 Parameters of the motion model of the dolphin body

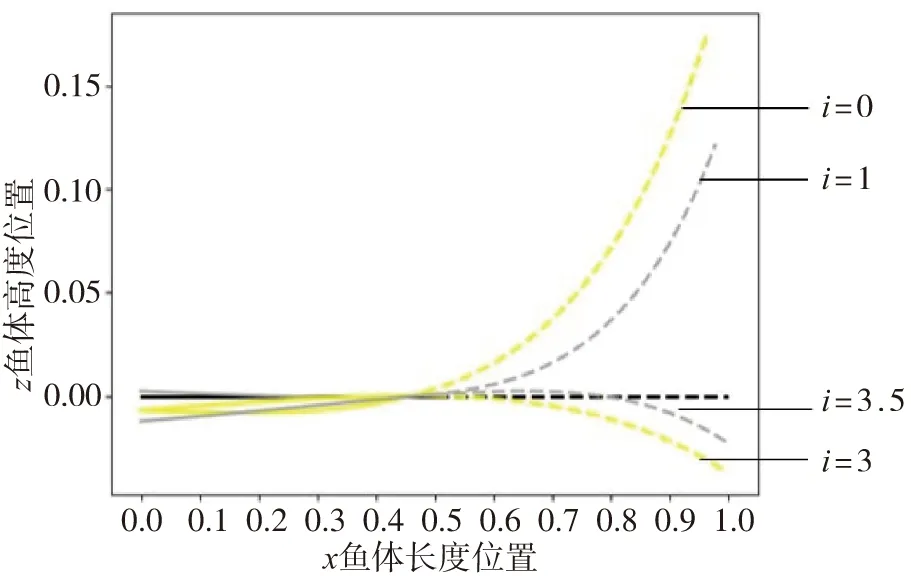
图3 豚体体干线摆动曲线Fig.3 Illustration of the dolphin body wave during swimming
1.3 机器鱼样机设计
根据生物形态特点与结构特征,设计了一种柔性仿生江豚机器鱼样机,主要由以下3部分组成:头部、尾部、鳍肢。设计样机全长为50 cm,其中头部占体长2/3,尾部占体长1/3。头部内置通信模块和控制模块,可采用无缆通信和有缆通信两种方式。头部与尾部连接有俯仰驱动机构,胸鳍固定于头部两侧起到稳流与平衡游动姿态的作用,同时这种形态有利于完成水下滑行动作,降低游动阻力以提高续航能力,仿生江豚机器鱼高机动性和高负载性可以满足长航时和大范围作业的需求。如图4所示为仿生江豚机器鱼三维模型,依据该模型真实还原制作了柔性机器鱼样机,图5所示为样机模型,表3为样机主要设计参数指标。

图4 仿生江豚机器鱼三维模型示意图Fig.4 3D model of a bionic robotic porpoise fish

图5 仿生江豚机器鱼样机Fig.5 Bionic robotic porpoise fish prototype

表3 仿生江豚机器鱼样机主要设计参数Tab.3 Main design parameters of the bionicrobotic porpoise prototype
2 仿生机器鱼数值模拟
2.1 计算参数
为计算仿生机器鱼水动力特性[29],表征豚体水动力特性的参数主要有升沉力系数Cl,阻力系数Cd和雷诺数Re
(8)
(9)
(10)
式中:Fz—豚体游动升沉力(N),Fx—豚体游动阻力(N),S—豚体湿表面积(m2)。规定沿z轴正方向为豚体游动升力方向,沿z轴负方向为豚体游动沉力方向。沿x轴正方向为豚体游动阻力正方向。
2.2 计算工况
计算域为圆柱形流场,长为6 L,流场直径为6 L。利用Curvature和Proximity算法对该计算域进行四面体非结构网格划分,网格最大面尺寸为0.1 m,最小单元尺寸设为5×10-3m,网格单元增长率为1.1,其余为默认设置,如图6所示为数值模拟网格划分结果。

图6 网格划分结果Fig.6 Structure of grids
计算域所涉及的介质为20 ℃液态水(密度ρ=998.2 kg/m3,黏度μ=1.003×10-3N·s/m2)。域的左边界设置为速度v=15.3 m/s(即55 km/h)[20]的速度入口,初始压强为0 Pa,而右边界设置为压力出口。图7为计算域示意图。

图7 计算域示意图Fig.7 Illustration of computational domains
在ANSYS Fluent 2020R2版本中,设置Coupled算法和Third-Order MUSCL离散算法求解SSTk-w两方程湍流模型。其余为默认设置。
2.3 水动力性能计算
图8所示为数值模拟速度云图。流场中沿鱼体x轴方向,鱼体表面速度先增大后减小,江豚前部流速明显加快,在外流场压力差的作用下包裹涡旋在前部,而尾部表面涡旋脱落明显。江豚通过弯曲体干线控制周身的水流与身体表面的边界层分离,以涡旋的形式脱出,在江豚后侧会形成产生推进力的尾涡和尾流,尾流可被认作由涡旋产生的向后喷出的射流[31]。前部的涡旋较好地包裹在表面,而尾部的涡旋则脱落明显,所以尾涡主要由尾部脱落产生,并且后侧的尾涡结构随摆幅变化呈变大和变小的趋势。

图8 不同摆动角下的速度云图Fig.8 Velocity clouds at different oscillation angles
江豚在下潜游动过程中,不仅获得升沉力,也受到游动阻力。前侧形成较大的正压强,而后侧形成较小的正压强,形成从前向后的正压强差,阻碍江豚向前游动。江豚尾部形状的改变会引起游动阻力和升沉力的变化,见表4。相比于滑翔状态的豚体阻力系数0.001 693,当尾部上摆时,阻力系数先减少后增大,当摆动角θ为13.45°时,阻力系数下降为0.001 683,减幅为0.6%,当摆动角θ增大到18.93°时,阻力系数上升到0.001 798,增幅为6.2%;而当尾部下摆时,阻力系数先增大后减少,当摆动角θ为-2.57°时,阻力系数上升到0.001 751,增幅为3.4%,当摆动角θ为-4.17°,阻力系数为0.001 704,增幅为0.6%。

表4 不同摆动角下的水动力学系数Tab.4 Hydrodynamic coefficients at different swing angles
3 样机试验
为进一步分析仿生江豚机器鱼在移动投饲作业中的可行性,根据本研究的CFD水动力学数值模拟与背腹式推进运动学模型,利用柔性仿生材料制作仿生江豚机器鱼样机,在上海海洋大学进行样机池塘实地试验。试验地点为开放水域环境,并进行多次鱼群共融性样机测试。
仿生江豚机器鱼以半径约为1.5 m的范围内进行水平面回旋游动,18 s内池塘中鱼群出现聚集现象,且出现跟随机器鱼游动的现象,如图9所示,为了区分池塘中所养殖的鱼群,机器江豚为红色样机。机器鱼以约为0.5 m/s的速度游动,t=0 s时池塘中鱼为个体游动;t=3 s时周围鱼群向机器鱼方向游动;t=6 s时机器鱼周围聚集较多鱼群;t=9 s后鱼群发生跟随效应,跟随机器鱼尾流轨迹进行游动。在试验中,样机多次游动均有集鱼现象与鱼群跟随游动现象。

图9 仿生江豚样机池塘游动试验Fig 9 Bionic porpoise prototype pond swimming experiment
具有流线型的仿生江豚机器鱼面向未来智能化移动投饲和养殖监测的研究方向,载荷量大、续航力强,且游动速度可达0.5 m/s,具有游动效率高、与鱼群环境共融的优势。航行过程中,基于背腹式推进运动模型,实现了鱼群的共融,通过试验发现鱼群会跟随机器鱼游动轨迹进行集群游动,有效达到了移动投饲的效果。相关研究[31-33]也发现仿生鱼的不同行为对斑马鱼的集群、应激等行为有不同的影响机制,在样机试验测试过程中,发现不同颜色江豚机器鱼、不同摆动频率与摆动幅度时,对于鱼群的诱集均有不同的效果,因此在后续的研究中可以针对不同的游动参数[34]对鱼群共融性进行研究探索。
4 结论
在仿生江豚机器鱼的设计研究中,背腹式推进方式的游动为其提供了强大动力,构造流体外型对游动阻力的减少至关重要。数值模拟结果显示,摆动角θ=0°的阻力系数为0.001 693,θ=13.45°的阻力系数为0.001 683,而θ=18.93°的阻力系数为0.001 798,该阻力系数数值相较于规则几何形体较小,而刚性椭球体阻力系数约为0.5左右,因此推测流型与柔性体对于生物游动提高推进效率具有重要影响机制。研究设计了一种可用于智能水产养殖的共融性仿生机器鱼,移动投饲机器鱼可辅助相关养殖设备进行移动投饲,也可通过搭载水质参数传感器完成养殖水环境动态监测与鱼群监测,更好地服务与水产养殖的现代化与智能化。
□
