木质纤维素酶水解分形动力学的研究进展*

解先利，刘云云，曹运齐，赵元元，陈世贤

木质纤维素酶水解分形动力学的研究进展*

解先利，刘云云†，曹运齐，赵元元，陈世贤

（陕西科技大学 机电工程学院，西安 710021）

酶水解作为发酵法生产燃料乙醇的关键步骤之一，其高效的转化过程对后续糖发酵至关重要，酶水解动力学研究可为高效转化机理的研究提供理论支持。但纤维素酶水解是一个复杂的多相异质反应过程，很难用简单的动力学模型进行表征。由于酶分子表面具有分形特性，其与分形动力学具有局部相似性，因此，分形理论可为木质纤维素酶水解的复杂动力学研究提供理论基础。从纤维乙醇生产工艺出发，在分析木质纤维素酶水解机理及影响酶解效率主要因素的基础上，总结了国内外分形动力学目前用于木质纤维素类生物质酶水解过程的主要动力学模型研究进展，并对其发展趋势和应用前景进行了展望。

木质纤维素；酶水解；燃料乙醇；动力学模型；分形动力学

0 引 言

木质纤维素类生物质是地球上储量最丰富的可再生资源，主要包括农作物秸秆、林业废弃物、畜禽排泄物等，其纤维素含量可观，将其转化为能源可缓解化石燃料短缺的危机，同时可减少环境污染问题[1-2]。将木质纤维素类生物质转化为纤维乙醇，称为第二代燃料乙醇。与第一代以粮食为原料的燃料乙醇相比，纤维乙醇不仅解决了“人粮危机”，而且使废弃资源变废为宝得到资源循环利用[3]。纤维乙醇的生产一般需要经过原料预处理、酶水解和发酵过程的转化。酶水解是纤维乙醇生产过程中的关键步骤，其需要微生物蛋白酶的参与，反应过程十分复杂。再者，参与反应的生物质具有多样性并且结构复杂，使得酶与底物的接触过程存在一定的困难，加上产物的反馈抑制效应等，这些问题均增加了酶促反应的难度。研究分析酶水解过程的反应动力学有助于酶促反应过程开发和生物反应器的优化设计等。分形理论作为酶促反应研究的有效方法之一，其从抽象的研究对象及复杂非线性系统入手，可真实反映物质的内在联系。分形理论最基本的特点是采用分维的数学方法研究客观事物，不仅可以精确描述复杂系统的真实属性与状态，而且更加符合客观事物的多样性和复杂性。因酶分子表面的分形特性，可采用分形语言对酶催化动力学进行描述，“酶分形动力学”的概念也因此产生[4-5]。分形表面上酶反应的速率与表面积或颗粒半径等均有关。“酶分形动力学”模型以分形维数和反应速率常数两个衡量指标，可揭示加酶量、反应时间和底物浓度等条件对反应过程的影响，有力简化了纤维素酶促反应机理研究。反应速率主要衡量酶催化反应的快慢，分形维数主要衡量酶与底物之间的作用关系，如用分形维数衡量底物颗粒的不规则性，底物越不规则，其与酶之间的有效吸附能力越差。本文首先概述分形理论，其次阐述纤维乙醇转化理论基础，最后总结国内外分形动力学目前用于木质纤维素类生物质酶水解过程的主要动力学模型，并展望了其应用前景。

1 分形理论的概述

分形理论是描述自然界中不规则、复杂事物，揭示隐藏在复杂现象背后的规律、局部和整体之间的本质内在关联性的一种分析方法[6]。分形理论最早是由法国科学家曼德尔布罗特（Mandelbrot）于20世纪70年代，通过对不规则几何形状体的观察和分析后首次提出[7]，之后迅速成为人们研究和处理自然与工程事件中无规则形体的强有力的理论分析工具。随着研究领域的不断深入和拓宽，分形理论也得到进一步扩展并广泛应用于建筑[8]、中药[9]、木材[10]、地质灾害[11]等众多领域的研究中。

经典欧式几何学确定了小尺度上点、线、面之间的关系，并提出确定物质中任意位置所需的独立坐标为欧式维数。欧氏维数通常为整数，如点的维数是0，直线的维数是1[12]，其缺点在于对不规则几何物体的特性不能进行描述，因此需要引入分形。分形是一种粗糙或破碎的几何图形，其组成部分可被无限细分，且其细分部分的形状一般与图形整体形貌相似。分形以某种方式在局部和整体方面呈现自相似性、标尺不变性、可迭代性和无限不规则等特点，其中由于图形具有自相似性，产生了分形维数（fractal dimension）[12-13]。在分形理论研究中，分形维数描述不同分形体系特征的定量参数，是对分形体系具有的复杂结构及其细微变化进行量化描述和表征的重要工具。分形维数与经典欧氏几何学中的整数维不同之处在于分形维数一般是小数，能更精确地描述自然形体。分形理论中，物质越复杂，则分形维数越大，其非整数部分也被称为分形维数。分形维数反映了酶水解反应速率的时间迟滞性，且变化范围在0 ～ 1之间。均相反应中认为物质是在三维空间中的分子扩散运动，而非均相的木质纤维素酶水解过程中，易水解底物不断被消耗，难水解底物占比越来越多，物质的扩散速率不断减小，反应速率也会随着反应的进行不断降低，这导致了反应速率具有时间迟滞性。

分形维数有多种计算方法，如盒维数法、尺码法、功率谱密度法、半方差法和轮廓均方根法等，如图1所示[14-15]。

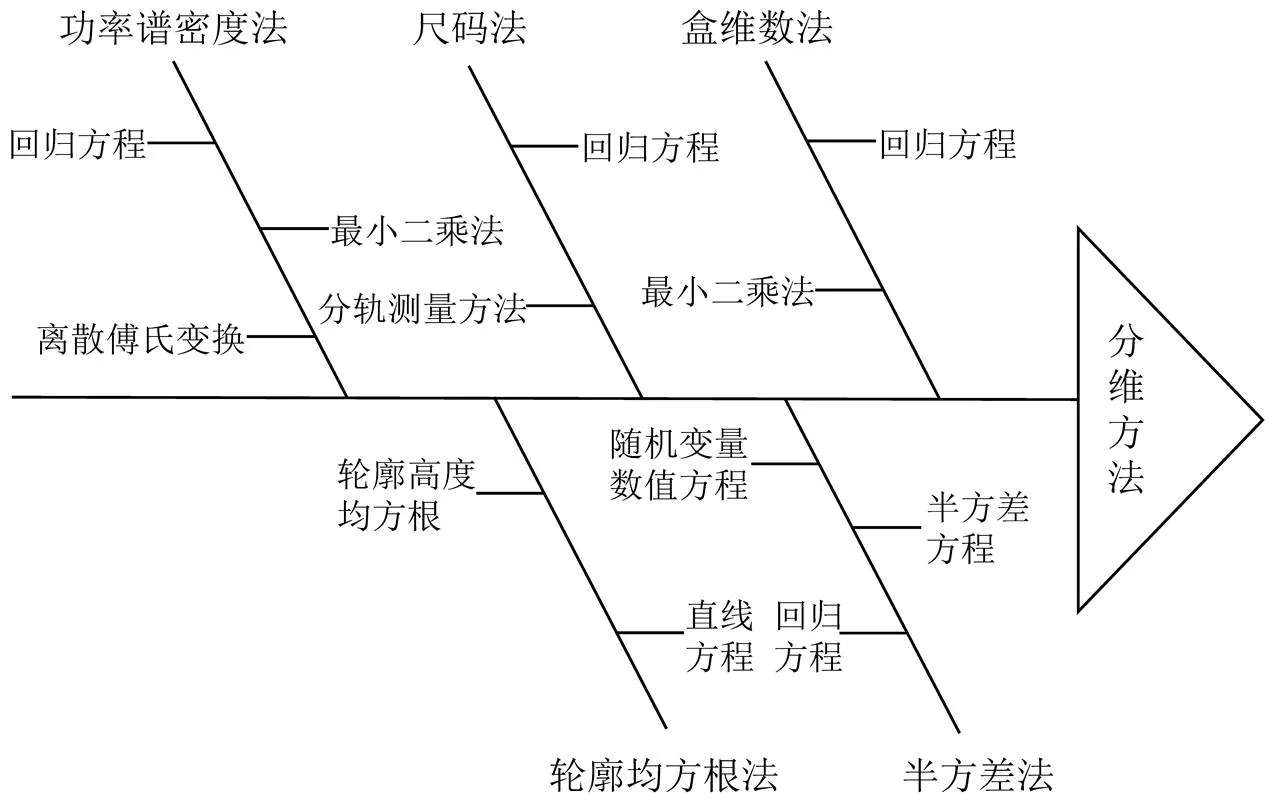
图 1 分形维数的计算方法[14-15]

蛋白质、酶等生物有机体结构复杂、分子量大，且表面粗糙、结构不均匀，是典型的分形研究体系，适合使用分形维数对其进行特征描述。当前，分形理论仍处于研究阶段，其应用还存在一些不足。分形理论在酶分子应用方面主要是基于酶分子及其表面具有的分形特性与分形动力学具有局部相似性，因此，酶的催化动力学可用分形语言进行描述。酶水解动力学与分形理论结合即为“酶分形动力学”。酶催化反应动力学的研究最早始于经典的米氏方程（Michaelis-Menten equation）及其准稳态假设，但是研究表明，在限定维数或非均相条件下发生酶催化反应时，底物和酶的扩散一般难以达到准稳态假设的要求，此时米氏方程对酶催化动力学的表征就会出现较大的偏差。因此，酶促反应的探索长期以来主要集中在基于米氏方程，利用分形理论修正传统的米氏方程以准确模拟酶催化反应过程的研究方面。纤维素类生物质的酶水解是生产燃料乙醇的关键过程，通过建立反应动力学方程研究酶催化反应历程，对燃料乙醇生产工艺优化和反应器的设计具有重要的指导意义，将分形理论应用于木质纤维素酶水解过程可为酶水解的复杂动力学研究过程提供理论依据。

2 纤维乙醇转化理论基础

2.1 纤维乙醇生产工艺

纤维乙醇主要是指以生物质为原料通过糖化发酵等过程转化而产生的一种液体燃料，可以直接作为动力燃料或者作为燃油改善剂[16]。木质纤维素类生物质储量丰富，是生产乙醇最有前景的可再生资源。纤维乙醇的生产主要包括五个过程[17]：原料的预处理，纤维素预水解，水解液的解毒，糖化发酵以及乙醇蒸馏提纯（如图2所示）。纤维乙醇提纯后添加一定的变性剂即为燃料乙醇。燃料乙醇是一种非常重要的生物质液体燃料，可以直接作为动力燃料或者是掺入汽油中作为燃油改善剂和部分汽油的替代品。用汽油发动机的汽车，汽油中乙醇加入量在5% ～ 22%；而对于乙醇专用发动机的汽车，乙醇加入量一般在85% ～ 100%[18]。因此，发展燃料乙醇技术，不仅可以缓解能源危机，乙醇燃烧过程污染物排放量少，同时减少了有害气体的排放，且排放的CO2可被生物质吸收，实现了碳平衡，有效地改善了生态环境。

图2 木质纤维素生物生产乙醇的流程图[17]

2.2 酶水解机理

木质纤维素类生物质主要化学成分包括纤维素、半纤维素和木质素，三者通过化学键链接，形成纤维原料致密、复杂的化学结构。纤维原料经过预处理后，底物中多糖组分可通过酸水解或者酶水解降解为可发酵单糖。

与酸水解方式相比，纤维底物酶法水解因条件温和、专一性强、易于控制且副产物少而被广泛应用于燃料乙醇的生产过程。纤维素酶是一种多酶复合物，主要由三种酶组成：1,4--D-葡聚糖纤维二糖水解酶、1,4--D-葡聚糖水解酶、-D-葡糖苷酶，分别称为外切葡聚糖酶、内切葡聚糖酶和纤维二糖酶，酶水解过程是多种酶协同作用共同降解底物的过程。

木质纤维素的酶水解是非均质多相反应[19]其主要过程如图3所示[20]。首先纤维素酶通过结合域吸附到底物上，再作用到底物表面的易水解键，纤维素酶与底物之间形成酶−底物络合物；其次-糖苷键水解同时纤维素酶沿着纤维素链向前移动，最后纤维素酶从底物上脱附，-葡萄糖苷酶将纤维二糖水解成葡萄糖。目前，纤维素酶降解底物的过程普遍认为是通过协同理论完成的[21-22]。协同作用的观点认为，结晶纤维素降解主要通过外切葡聚糖酶从链端断开-1,4糖苷键进行。内切葡聚糖酶仅从内部断开-1,4糖苷键，出现分裂状开放式活性中心。外切葡聚糖酶和内切葡聚糖酶生成的产物是纤维二糖或葡萄糖，其对酶的活性存在抑制作用。因此纤维素的有效水解须在-葡糖苷酶的作用下打开最终的糖苷键使纤维二糖降解为单糖葡萄糖[22]。纤维底物的降解是多种酶协同作用的结果，商业纤维素酶的成本过高是当前制约燃料乙醇产业化发展的主要瓶颈[23-24]。

图3 纤维素酶水解木质纤维素过程[20]

2.3 酶水解的影响因素

从酶水解反应动力学角度分析，影响木质纤维素酶水解速度的因素主要有：酶解底物、纤维素酶和分形等因素[25]。具体包括：（1）底物物性相关常数主要有底物结构及影响底物化学结构的预处理方式和预处理时间等因素；（2）纤维素酶水解条件主要包括酶水解温度、pH值、表面活性剂、超声波、O2等一些辅助酶水解条件，这些因素会影响反应速率常数、吸附平衡常数、酶与底物的亲和力[26]；（3）底物初始浓度、反应浓度和酶的初始浓度；（4）其他因素，如抑制剂和活化剂。

木质纤维素酶水解效果的提高对后续发酵过程至关重要。目前，提高木质纤维素酶水解效果主要有以下几种措施：（1）对原料进行有效预处理以打破底物致密的化学结构，去除木质素，提高纤维素酶与纤维底物的接触面积，以利于酶水解过程；（2）高效纤维素酶的生产；（3）酶解过程添加表面活性剂[27]等酶促反应助剂；（4）利用纤维素酶固定化技术来提高酶的作用效果；（5）酶解抑制作用的改善等。

3 纤维素酶水解反应分形动力学模型

3.1 纤维素酶水解动力学

普遍认为，酶水解是复杂的固−液两相催化过程，涉及分子传质动力学和反应动力学，一般可将其反应过程简化为图4所示模型：首先是木质纤维素在内、外切葡聚糖酶作用下被水解为纤维二糖的固相过程；其次是纤维二糖被-葡萄糖苷酶水解为葡萄糖的液相过程[28]，两个过程紧密联系。由于两个反应阶段的复杂多变性，使得酶水解动力学的研究较为困难，不能用简单的动力学参数来表征木质纤维素酶水解过程。

图4 纤维素酶水解简化模型[28]

根据底物酶水解反应的主要过程，纤维素酶水解动力学模型一般可概括为以下五类：经验模型、米氏模型、吸附模型、可溶底物水解模型和分形动力学模型，如表1所示。经验模型采用数理统计拟合方法，确定底物理化性质与水解时间之间的定量关系，在一定程度上阐明了水解性质，该机理模型通用性强，可较全面揭示水解机理，得到优化参数。但存在实验量大、耗时较长等缺点。

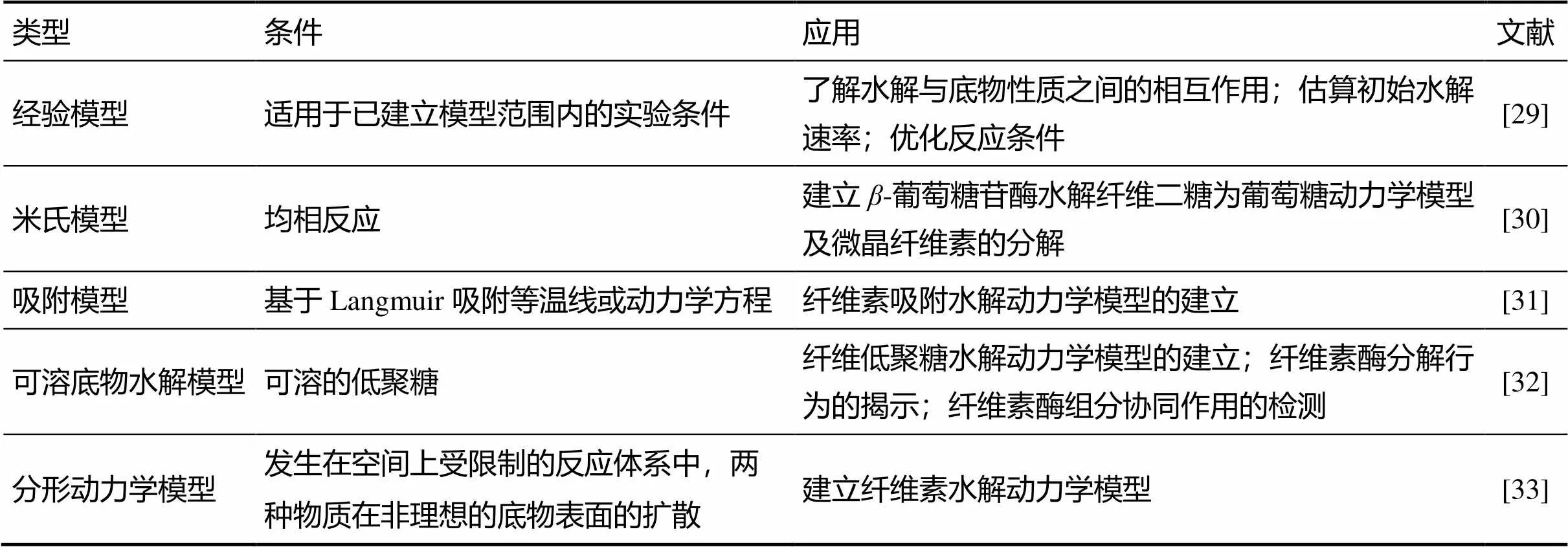
表1 几种动力学模型特点及应用

米氏模型是基于质量作用定律而得出[34]，适用于均质反应条件，但可作为-葡萄糖苷酶将纤维二糖转化为葡萄糖的动力学研究模型[35]。米氏模型在纤维素吸附水解过程中采用Langmuir吸附等温线动力学方程，但在涉及非理想底物的催化反应中，必须考虑底物浓度不均和分形动力学等因素。此类模型往往不能直接应用到不溶性底物的水解，主要是由于酶在不溶性底物上作用的非均相特性和底物可及性末端的分布与浓度造成的。但可溶性水解模型可深入分析纤维素水解生成的寡糖能否被内、外切葡聚糖酶降解水解机制。TING等[36]建立一个随机性模型，深入研究了纤维素酶的模块化特性。催化域（catalytic domain, CD）和纤维素结合域（cellulose binding domain, CBD）被模拟成随机移动者，其动力学被偶联到底物表面纤维素链接的压缩/扩展和纤维素链的迁移。

分形动力学模型是在传统米氏方程基础上对其修正而建立的更为准确的动力学模型。分形动力学在酶促反应机理研究方面的应用，不仅简化了酶水解反应的复杂性，而且为设计开发新的水解反应器、预测酶促反应规律、提高酶促效果等方面发挥了重要作用。学者们通过假设和条件简化提出了不同反应条件[20,37]下的各种动力学模型，假设和条件简化的适用性和合理性对模型参数值存在较大影响。

3.2 分形动力学模型的建立

近年来，针对木质纤维素酶解过程中存在的主要问题，如底物结构的复杂性，由于平行和连续反应引起的复杂反应网络，内切葡聚糖酶、纤维素酶和-葡萄糖苷酶（除辅助酶之外）等几种酶的协同作用，酶−底物和酶−效应物的化学吸附、物理吸附、传质、抑制和失活相互作用等[38-39]，研究人员提出了各种不同的分形动力学模型以研究木质纤维素酶水解过程的反应规律，并且取得了一定的进展。

SAVAGEAU[40]首次使用幂函数公式研究了分形介质中的米氏动力学模型，其经典的酶催化反应如式（1），由两个明显的限速方程式（2）和式（3）表示。该法认为酶催化反应机制中，生成产物的速率要慢于底物与酶复合物的可逆反应的速率。因此，产物生成的速率决定整个酶催化反应的速率。

式中：为酶；为底物；为酶−底物复合体；是产物；1和2分别为吸附和脱附速率常数；3为产物形成的速率常数。

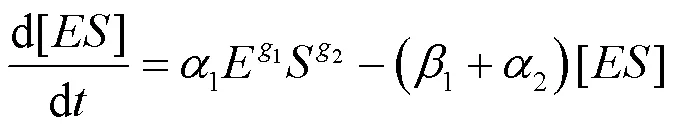
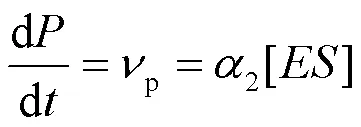
式中：p为产物形成的速率；1、2和1是幂函数公式新引入的参数；1和2分别为与底物和酶有关的速率级数。

VALJAMÄE等[41]首次采用分形动力学对木质纤维素酶水解的过程进行拟合，利用以下经验模型，描述了酶水解过程中纤维二糖随时间的变化规律：

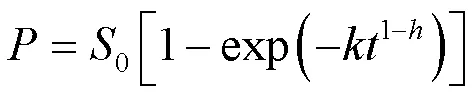
式中：、0分别为生成的纤维二糖浓度和底物总糖浓度；为时间；、分别为反应速率常数和底物

分形维数。

随着分形理论的发展，研究人员不断采用各种分形动力学模型研究酶水解过程中的复杂纤维素催化动力学。WANG等[42]基于一阶纤维素降解动力学模型，并结合20世纪80年代KOPELMAN[43]提出的可以实现对异质动力学过程描述的分形动力学模型，建立了关于葡萄糖转化率与时间的表达式：

式中：为葡萄糖转化率；、0分别代表反应剩余糖浓度和底物中的总糖浓度。

张宇等[44]利用类分形动力学对NaOH、HCl和高温液态水三种不同的预处理方法进行比较，假定纤维素复合酶对不溶性纤维素底物为单一酶作用，受到限制的底物−纤维素酶异相反应，发生在纤维素酶表面上，并且随着反应的进行，底物越来越难水解。因此，假设反应速率与时间呈幂函数关系，同时将纤维素酶水解看作拟态的一级反应，得到还原性糖与时间的表达式：

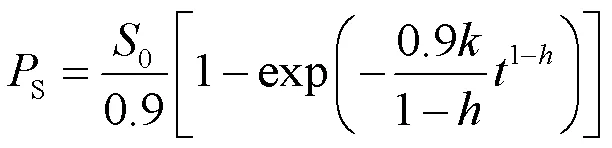
式中：S、0分别为生成葡萄糖浓度和底物总糖浓度。

上述已建立的木质纤维素酶水解分形动力学模型，首先，前期研究主要对经典的米氏方程进行了修正，将幂函数公式用于分形介质中得到上述酶水解分形动力学模型，即米氏动力学模型。相比于其他分形动力学模型，其方程相对复杂，且存在参数较多不易确定和难以计算等缺点，但其丰富了酶催化反应的研究途径。其次，利用分形理论建立的分形动力学都是在KOPELMAN描述的分形动力学方法的基础上推导出来的，与经典的米氏动力学酶催化反应模型相比，分形动力学模型能够用于多种条件下的复杂动力学研究，且模型更加简洁、参数少且易确定等，可进一步为木质纤维素酶水解过程中酶−底物之间的相互作用提供理论依据。最后，上述的动力学模型虽然方法不同，其结果也各异，但都是利用分形理论对酶促反应过程进行了更准确的描述和表征，为非线性理论用于木质纤维素酶水解过程的研究开辟了新的研究途径。

3.3 分形动力学模型的应用

纤维素−纤维素酶之间的反应一般受到三维限制且发生在分形表面上，使得反应速率常数不断减小，故研究者假定速率常数与时间的数学关系从而提出以速率常数和分形维数为参数的分形动力学模型，用于描述各种复杂条件下的木质纤维素类酶水解过程，通过非线性回归拟合可得出二者之间的关系式。大量实验表明，速率常数与底物特性、酶用量及其活性有关。分形维数主要表征酶水解反应速率的时间迟滞现象，为反应的内在特征参数，其变化范围一般在0 ～ 1之间[13,43]，并且随底物添加量和酶用量变化而变化[45]；预处理和酶解条件也会对分形动力学参数产生影响，如预处理温度[46]、反应介质中添加非离子表面活性剂或聚合物[46]以及各种抑制剂；分形维数还与搅拌器的搅拌速度有关[47]。由以上分析可见，速率常数和分形维数能够反映底物特性、反应条件以及酶的可及性等对木质纤维素酶解糖化的高效转化的影响，故分形动力学是描述各种复杂条件下的酶水解过程的有力工具。

ZHANG等[48]在研究NaOH、HCl和高温液态水三种预处理方法对甘蔗渣酶水解效果的影响过程中，采用分形的方法对酶解过程进行非线性回归拟合，结果发现添加吐温80/木聚糖酶后，反应速率、酶解率和糖回收率明显升高，且反应过程主要取决于速率常数而不是分形维数。

WOJTUSIK等[47]在蒸汽爆破条件下对玉米秸秆预处理，研究了玉米秸秆的酶水解反应动力学。实验拟合了两种动力学模型：经验模型和分形模型。在前一种情况下，随着搅拌速度的增加，整体序列指数从13显著降低到2，这表明酶对纤维表面的可及性增加。分形动力学模型与实验结果拟合性更好，在低搅拌速度条件下具有更小的偏差。随着搅拌速度的增加，分形反应速率常数增加；在250 r/min及以上达到稳定值。分形维数随着搅拌速度的增加而减小，直至约为0.19，表明酶对底物的可及性更高。

WANG等[42]用分形动力学分析了纤维素酶负载量、底物性质、反应介质中添加非离子表面活性剂/聚合物对木质纤维素酶水解过程的影响，结果发现反应速率随着纤维素酶用量的增加而增大；添加非离子表面活性剂/聚合物增加了反应速率，同时可以降低分形维数，证明了纤维素酶水解反应的复杂动力学可以用分形动力学模型进行描述。

AGUIAR等[49]在水蒸气处理甘蔗渣的研究中利用分形动力学模型，对比了预处理方法和不同洗涤工艺对底物可及性的影响。结果发现，与其他预处理方法的反应速率值相比，磷酸预处理和水洗条件下产生的底物最易被水解，能够促进反应速率的增大。较低的分形维数表征了更易水解的底物其具有较高的非晶特性。而碱洗过程自水解产生的底物与酶最不易接触。较高的分形维数值通常与蒸汽处理底物中的高木质素含量有关，因为木质素的存在导致酶的无效吸附，从而降低了部分游离酶与底物的接触。

综上所述，分形理论作为一种研究酶解反应动力学的有效工具，已被学者广泛研究，并在酶水解机理研究方面取得了一定进展，这些研究工作为纤维乙醇高效转化技术的开发奠定了理论基础。酶分形动力学模型建立在传统米氏方程基础之上，其通过反应过程条件最终确定速率常数和分形维数的关系式，实现对复杂非线性反应过程的描述。由上述文献分析可知，酶分形动力学研究的关键问题是认识酶催化反应分形动力学与传统米氏动力学之间的区别，并针对其分形特性进行模拟，这也是酶促反应动力学研究的趋势。随着分形理论的不断发展，酶分形动力学的研究也将不断完善。

4 结语与展望

酶水解作为发酵法生产燃料乙醇的关键步骤之一，受到研究者的广泛关注。分形理论作为酶催化反应研究的有效方法之一，近年来不断被应用于木质纤维素酶水解过程。随着分形理论的不断发展与完善，须建立更简单、准确的酶水解动力学模型，进而阐明酶水解反应历程，为提高木质纤维素酶水解复杂的多相异质反应过程提供更好的改善路径。明确酶分形动力学与传统米氏动力学的区别，并针对酶分形动力学特性建立模型，是酶促反应动力学研究的关键问题。

[1] 任利枢. 我国农业废弃物处理现状[J]. 畜牧兽医科技信息, 2019(8): 35-35.

[2] 严铠, 刘仲妮, 成鹏远, 等. 中国农业废弃物资源化利用现状及展望[J]. 农业展望, 2019, 15(7): 62-65. DOI: 10.3969/j.issn.1673-3908.2019.07.014.

[3] SATARI B, JAISWAL A K. Green fractionation of 2G and 3G feedstocks for ethanol production: advances, incentives and barriers[J]. Current opinion in food science, 2021, 37: 1-9. DOI: 10.1016/J.COFS.2020.07.004.

[4] Seibert E, Tracy T S. Fundamentals of enzyme kinetics[J]. Enzyme kinetics in drug metabolism, 2014: 9-22.

[5] 张雨薇. 生物大分子分形维数的计算及酶的分形反应动力学模拟[D]. 天津: 天津大学, 2007: 16-18. DOI: 10.7666/d.y1358818.

[6] 张济忠. 分形[M]. 北京: 清华大学出版社, 1995.

[7] MANDELBROT B B. The fractal geometry of nature[M]. New York: W.H. Freeman, 1983.

[8] 贾艳艳. 基于分形理论的建筑解析[J]. 工业设计, 2019(3): 88-89. DOI: 10.3969/j.issn.1672-7053.2019.03.041.

[9] 俞梦莹, 万丹娜, 邵峰, 等. 分形理论在中药领域中的应用[J]. 中国现代应用药学, 2019, 36(12): 1592-1595. DOI: 10.13748/j.cnki.issn1007-7693.2019.12.028.

[10] 许威, 张绍群, 陈光伟, 等. 分形理论在木材断裂研究中的应用与进展[J]. 木材加工机械, 2011, 22(6): 36-39. DOI: 10.3969/j.issn.1001-036X.2011.06.012.

[11] 王潇, 刘婷, 姚昆, 等. 分形理论在达州市达川区滑坡灾害研究中的应用[J]. 人民长江, 2019, 50(2): 144-150. DOI: 10.16232/j.cnki.1001-4179.2019.02.025.

[12] 柳咪. 相思木乙酸预处理及酶水解过程的分形表征[D]. 西安: 陕西科技大学, 2016: 7-8.

[13] 柳咪, 迟聪聪, 龚亚辉, 等. 木质纤维素酶水解分形动力学的研究进展[J]. 中国造纸, 2015, 34(8): 62-67. DOI: 10.11980/j.issn.0254-508X.2015.08.013.

[14] 李茂盛, 王坤, 曹宇. 分形理论在零件接触分析中的应用研究[J]. 南方农机, 2019, 50(17): 35-36, 40. DOI: 10.3969/j.issn.1672-3872.2019.17.024.

[15] 李伯奎, 杨凯, 刘远伟. 分形理论及分形参数计算方法[J].工具技术, 2004, 38(12): 80-84. DOI: 10.3969/ j.issn.1000-7008.2004.12.030.

[16] 曹运齐, 刘云云, 胡南江, 等. 燃料乙醇的发展现状分析及前景展望[J]. 生物技术通报, 2019, 35(4): 163-169. DOI: 10.13560/j.cnki.biotech.bull.1985.2018-1002.

[17] BABU V, THAPLIYAL A, PATEL G K. 生物燃料生产[M]. 华炜, 译. 北京: 中国石化出版社, 2016.

[18] 余强, 庄新姝, 袁振宏, 等. 木质纤维素类生物质制取燃料及化学品的研究进展[J]. 化工进展, 2012, 31(4): 784-791. DOI: 10.16085/j.issn.1000-6613.2012.04.020.

[19] 尉慰奇. 桉木原料的预处理及其酶解糖化的研究[D]. 广州: 华南理工大学, 2012: 30-40.

[20] BANSAL P, HALL M, REALFF M J, et al. Modeling cellulase kinetics on lignocellulosic substrates[J]. Biotechnology advances, 2009, 27(6): 833-848.DOI: 10.1016/j.biotechadv.2009.06.005.

[21] GUPTA R, LEE Y Y. Mechanism of cellulase reaction on pure cellulosic substrates[J]. Biotechnology and bioengineering, 2009, 102(6): 1570-1581. DOI: 10.1002/ bit.22195.

[22] FUJII M, MORI J I, HOMMA T, et al. Synergy between an endoglucanase and cellobiohydrolases from[J]. The chemical engineering journal and the biochemical engineering journal, 1995, 59(3): 315-319. DOI: 10.1016/0923-0467(95)02996-6.

[23] FANG X, SHEN Y, ZHAO J, et al. Status and prospect of lignocellulosic bioethanol production in China[J]. Bioresource technology, 2010, 101(13): 4814-4819. DOI: 10.1016/j.biortech.2009.11.050.

[24] CHENG J J, TIMILSINA G R. Status and barriers of advanced biofuel technologies: a review[J]. Renewable energy, 2011, 36(12): 3541-3549. DOI: 10.1016/j.renene. 2011.04.031.

[25] GAO D H, CHUNDAWAT S P S, SETHI A, et al. Increased enzyme binding to substrate is not necessary for more efficient cellulose hydrolysis[J]. Proceedings of the national academy of sciences of the united states of America, 2013, 110(27): 10922-10927. DOI: 10.1073/ pnas.1213426110.

[26] VON SIVERS M, ZACCHI G. A techno-economical comparison of three processes for the production of ethanol from pine[J].Bioresource technology, 1995, 51(1): 43-52. DOI: 10.1016/0960-8524(94)00094-H.

[27] ALKASRAWI M, ERIKSSON T, BÖRJESSON J, et al. The effect of Tween-20 on simultaneous saccharification and fermentation of softwood to ethanol[J]. Enzyme and microbial technology, 2003, 33(1): 71-78. DOI: 10.1016/ S0141-0229(03)00087-5.

[28] XU F, DING H S. A new kinetic model for heterogeneous (or spatially confined) enzymatic catalysis:contributions from the fractal and jamming (overcrowding) effects[J]. Applied catalysis A: general, 2007, 317(1): 70-81. DOI: 10.1016/j.apcata.2006.10.014.

[29] BERLIN A, MAXIMENKO V, GILKES N, et al. Optimization of enzyme complexes for lignocellulose hydrolysis[J]. Biotechnology and bioengineering, 2007, 97(2): 287-296. DOI: 10.1002/bit.21238.

[30] PRATTO B, DE SOUZA R B A, SOUSA R JR, et al. Enzymatic hydrolysis of pretreated sugarcane straw: kinetic study and semi-mechanistic modeling[J]. Applied biochemistry and biotechnology, 2016, 178(7): 1430-1444. DOI: 10.1007/s12010-015-1957-8.

[31] ZHANG H Y, HAN L J, DONG H M. An insight to pretreatment, enzyme adsorption and enzymatic hydrolysis of lignocellulosic biomass: experimental and modeling studies[J]. Renewable and sustainable energy reviews, 2021, 140: 110758. DOI: 10.1016/J.RSER.2021.110758.

[32] CARO I, BLANDINO A, DÍAZ A B, et al. A kinetic model considering the heterogeneous nature of the enzyme hydrolysis of lignocellulosic materials[J]. Biofuels, bioproducts and biorefining, 2019, 13(4): 1044-1056. DOI: 10.1002/bbb.1997.

[33] MOMOH O L Y, OUKI S. Development of a novel fractal-like kinetic model for elucidating the effect of particle size on the mechanism of hydrolysis and biogas yield from Ligno-cellulosic biomass[J]. Renewable energy, 2018, 118: 71-83. DOI: 10.1016/j.renene.2017.11.005.

[34] MICHAELIS L, MENTEN M L. Die kinetik der invertinwirkung[J]. Biochemische zeitschrift, 1913, 49(333-369): 352.

[35] BERRY H. Monte Carlo simulations of enzyme reactions in two dimensions: fractal kinetics and spatial segregation[J]. Biophysical journal, 2002, 83(4): 1891-1901. DOI: 10.1016/S0006-3495(02)73953-2.

[36] TING C L, MAKAROV D E, WANG Z G. A kinetic model for the enzymatic action of cellulase[J]. The journal of physical chemistry B, 2009, 113(14): 4970-4977. DOI: 10.1021/jp810625k.

[37] GAN Q, ALLEN S J, TAYLOR G. Kinetic dynamics in heterogeneous enzymatic hydrolysis of cellulose: an overview, an experimental study and mathematical modelling[J]. Process biochemistry, 2003, 38(7): 1003-1018. DOI: 10.1016/S0032-9592(02)00220-0.

[38] HSIEH C W C, CANNELLA D, JØRGENSEN H, et al. Cellulase inhibition by high concentrations of monosaccharides[J]. Journal of agricultural and food chemistry, 2014, 62(17): 3800-3805. DOI: 10.1021/ jf5012962.

[39] JALAK J, VÄLJAMÄE P. Multi-mode binding of cellobiohydrolase Cel7A fromto cellulose[J]. PLoS one, 2014, 9(9): e108181. DOI: 10.1371/journal.pone.0108181.

[40] SAVAGEAU M A. Michaelis-Menten mechanism reconsidered: implications of fractal kinetics[J]. Journal of theoretical biology, 1995, 176(1): 115-124. DOI: 10.1006/jtbi.1995.0181.

[41] VALJAMÄE P, KIPPER K, PETTERSSON G, et al. Synergistic cellulose hydrolysis can be described in termsof fractal-like kinetics[J]. Biotechnology and bioengineering, 2003, 84(2): 254-257. DOI: 10.1002/bit.10775.

[42] WANG Z L, FENG H. Fractal kinetic analysis of the enzymatic saccharification of cellulose under different conditions[J]. Bioresource technology, 2010, 101(20): 7995-8000. DOI: 10.1016/j.biortech.2010.05.056.

[43] KOPELMAN R. Fractal reaction kinetics[J]. Science, 1988, 241(4873): 1620-1626. DOI: 10.1126/science.241. 4873.1620.

[44] 张宇, 许敬亮, 袁振宏, 等. 甘蔗渣的不同预处理方法比较及其酶水解的类分形动力学[J]. 新能源进展, 2013, 1(2): 166-169. DOI: 10.3969/j.issn.2095-560X.2013.02.007.

[45] KIM T H, LEE Y Y. Pretreatment and fractionation of corn Stover by ammonia recycle percolation process[J]. Bioresource technology, 2005, 96(18): 2007-2013. DOI: 10.1016/j.biortech.2005.01.015.

[46] BOMMARIUS A S, KATONA A, CHEBEN S E, et al. Cellulase kinetics as a function of cellulose pretreatment[J]. Metabolic engineering, 2008, 10(6): 370-381. DOI: 10.1016/j.ymben.2008.06.008.

[47] WOJTUSIK M, ZURITA M, VILLAR J C, et al. Enzymatic saccharification of acid pretreated corn Stover: empirical and fractal kinetic modelling[J]. Bioresource technology, 2016, 220: 110-116. DOI: 10.1016/j.biortech.2016.08.069.

[48] ZHANG Y, DI X H, XU J L, et al. Effect of LHW, HCl, and NaOH pretreatment on enzymatic hydrolysis of sugarcane bagasse: sugar recovery and fractal-like kinetics[J]. Chemical engineering communications, 2019, 206(6): 772-780. DOI: 10.1080/00986445.2018.1525365.

[49] AGUIAR R S, SILVEIRA M H L, PITARELO A P, et al.Kinetics of enzyme-catalyzed hydrolysis of steam-exploded sugarcane bagasse[J]. Bioresource technology, 2013, 147: 416-423. DOI: 10.1016/J.BIORTECH.2013.08.067.

Research Progress on Fractal Dynamics of Enzymatic Hydrolysis of Lignocellulose

XIE Xian-li, LIU Yun-yun, CAO Yun-qi, ZHAO Yuan-yuan, CHEN Shi-xian

(College of Mechanical and Electrical Engineering, Shaanxi University of Science & Technology, Xi’an 710021, China)

Enzymatic hydrolysis is one of the key steps in bioethanol production with the fermentation method. The efficient enzymatic conversion process is significant for the subsequent sugar fermentation. The study of enzymatic hydrolysis kinetics can provide theoretical support for the study of efficient conversion mechanism. However, cellulose hydrolysis is a complex heterogeneous reaction, which is difficult to be described by a simple kinetic model. The fractal properties on the surface of the enzyme molecule have partial similarity to the fractal dynamics. Therefore, the fractal theory as theoretical support can be used to study the complex kinetics of lignocellulose hydrolysis. In this paper, the production process of cellulosic ethanol was introduced, and the main research progress of kinetic models of fractal dynamics applied to the enzymatic hydrolysis of lignocellulosic biomass was summarized based on the analysis of the hydrolysis mechanism of lignocellulose and the main factors affecting the hydrolysis efficiency, and its development trend and application prospect were finally prospected.

lignocellulose; enzymatic hydrolysis; fuel ethanol; kinetic model; fractal dynamic

2095-560X（2021）05-0426-08

TK6

A

10.3969/j.issn.2095-560X.2021.05.009

解先利（1993-），女，硕士研究生，主要从事生物质资源高效转化与利用技术开发。

刘云云（1984-），女，博士，副教授，硕士生导师，主要从事生物质资源高效转化与利用技术开发。

收稿日期：2021-07-12

2021-08-17

西安市科技计划项目（20193039YF027NS027）；陕西省自然科学基础研究计划面上项目（2021JM-382）；亚热带农业生物资源保护与利用国家重点实验室开放基金项目（SKLCUSA-b201802）；中国科学院可再生能源重点实验室开放基金项目（Y907k51001）

刘云云，E-mail：liuyu282009@126.com