基于时空图神经网络的交通拥堵预测技术

刘华 林立春 杨丽萍 洪东

随着全球定位和物联网技术的快速发展，道路上各种传感器采集的路网数据规模不断扩大。交管部门亟须针对已有的路网数据预测车辆未来的位置和区域分布，对道路前方可能发生的交通拥堵进行预警，并帮助驾驶员选择合适路线，从而缓解城市拥堵。文章采用时空图神经网络（STGNN）挖掘交通流量数据的潜在因果关系，对交通路网嵌入空间依赖和时间依赖进行建模分析。实验结果表明，该方案能更有效地预测未来的交通流量，防止发生拥堵。

时空图神经网络;交通流量;STGNN;拥堵预测

U491.1+13A411473

0 引言

近年来，通过对交通大数据的分析挖掘预测未来的交通趋势，已引起智能交通系统领域研究人员的广泛关注。准确预测未来的交通情况具有很多优势，它不仅可以帮助市民绕行拥挤的道路，而且可以提前安排高效的出行。由于大城市的交通每时每刻都在发生变化，相同位置的交通数据在不同时刻，如在工作日和周末会观察到不同的车流量;相同时刻的交通数据在不同位置也不相同，如在居民区和商圈附近也会观察到不同的车流量。因此，在交通数据中存在复杂的时空关系，这使得进行精确交通拥堵预测的任务极具挑战性。

早期的各种统计和机器学习技术，如整合移动平均自回归模型（ARIMA）、历史平均模型（HA）、支持向量回归（SVR）和卡尔曼滤波模型，已广泛用于交通预测。最近几年，图神经网络（GNN）在模拟现实交通中取得了很好的效果，它通过采用不同的特征聚集方案，将图中相邻节点之间的空间依赖性进行编码并融入其中。图卷积神经网络（GCN）[1-3]应用频谱卷积来学习结构依赖性和特征信息。Hamilton等[4]在GraphSAGE中进一步给出了空间域图卷积的通用框架，为图神经网络的研究打开了新的大门。后来有研究者把交通流模型转化为有向图上的扩散过程，并引入了扩散卷积循环神经网络（DCRNN），使用双向随机游走对空间依赖建模，使用循环神经网络捕获时间的动态性。最近越来越多的研究者利用时空图卷积网络（STGCN）[5-8]来解决交通领域的时间序列预测问题，使用卷积网络对空间和时间依赖关系进行建模。

在研究中发现，已有的模型无法明确捕获交通网络中目标节点的不同邻域节点对其的影响，同时基于循环神经网络（RNN）的模型也无法完成长期预测中的时间依赖性。为了解决上述挑战问题，本文给出一种高效的时空聚集方案来明确捕获不同邻域节点对目标节点流量的影响，并叠加时间点的嵌入，进而计算不同时间点之间的时间依赖性。与现有的流量预测模型相比，使用该方法可以显著提高预测的性能。

1 交通路网时空定义

交通网络用图形G=V，E表示，其中V是表示交叉路口节点的集合，E∈RV×V是图的邻接矩阵，如果节点i和j通过道路连接，则Ei，j=1，否则为0。

每个节点还包含交通流量、速度、占用率等路口的某些特征。不同节点上的交通流量随时间不断变化，采集的时间点之间的间隔一般为10 s至5 min。设定节点u在时间点t处的交通特征表示为Iu∈Rd，其中d表示路口特征维度;I∈RV×d代表时间点t时所有节点的流量特征;时间点t处的图表示为时间点图G，所有时间点图在结构上彼此相同。流量预测框架采用一系列T时间点图并将其节点特征I<1>，I<2>，……，I作为输入，并预测在接下来的N个时间点O，O，……，O上的节点流量强度。

2 基于时空图神经网络的交通预测方案

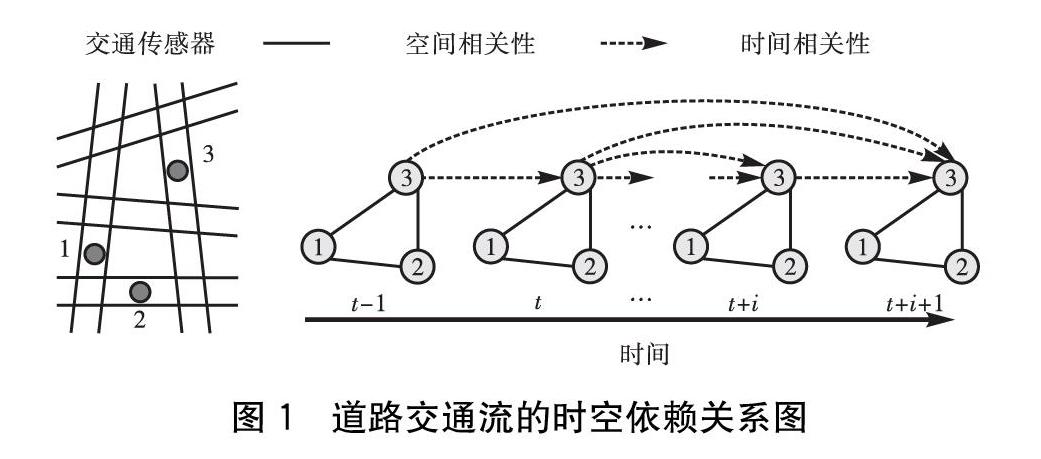
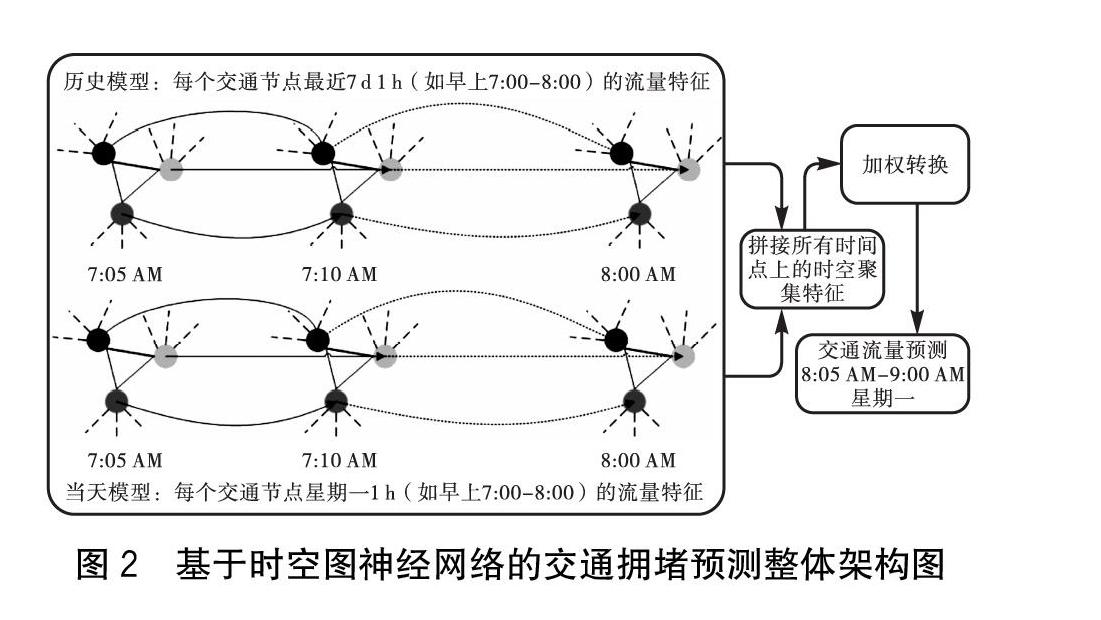
本节主要阐述利用时空图神经网络进行交通预测的方案，该方案可以有效地捕获道路交叉节点之间的时空依赖关系。如图1所示为简化的交通流时空依赖关系示意图。对此，设计了交通时空图和位置编码方案，分别用于执行时空聚集和捕获交通数据的周期性。在此基础上还定义了两种不同的时空聚集模型，即历史模型和当天模型，并给出了最终的嵌入和训练方法。交通预测方案的整体架构如图2所示，图中以预测星期一早上8：00-9：00的交通流量为例，历史模型取最近一周早上7：00-8：00的交通流数据，当天模型取星期一早上7：00-8：00的交通流数据。

时空图：为了捕获交通节点中不同时间点之间复杂的时空依赖关系，在连续时间点图的相同节点之间引入时间点连接边（图2），其中相同颜色的小圆圈表示相同的节点。为了学习节点的嵌入，在一个时空图上执行时空聚集，该图由来自预测窗口的前T个时间点图和时间点之间的连接边所组成。

位置编码：从一天中的不同时段提取大量的交通特征，需要在模型中对不同时间段的相对位置进行编码。为了遵循机器翻译中广泛使用的相对定位概念，本文使用具有正弦函数的位置编码来提供不同时间点的位置信息。由于必须确保每天的正弦函数在当天内完成一个完整的周期，因此任何持续时间段都可以表示为正弦曲线的重复部分，如正弦曲线在每天上午的时间段（7：05-8：00）将具有相同的模式。当然，还可能存在每周流量模式，如具有相同流量的特定日期，同时还需要查看模式是来自工作日还是来自周末。为了捕获这种每周模式，增加一个每周完整的正弦函数。式（1）实现了最终的位置编码。

M=sin2πt24×ds+sin2πt24×7×ds（1）

其中t表示给定的时间点;ds表示1 h内观察到的数据样本数。这个方法还可以扩展到按月捕获完整周期的正弦波。

时空聚集：本文设计了一种时空聚集方案，将空间和时间依赖性进行编码并嵌入到交通节点中，它具有三个组成部分，分别是空间依赖性建模、时间依赖性建模、时空嵌入连接建模。接下来将详细介绍。

2.1 空间依赖性建模

在现实交通网络中可以观察到，所有高阶邻域对于目标节点的重要性并不相同，因此應该捕获不同跳邻域节点所携带的不同信息。式（2）表示在每个时间点图中分别对不同邻域中的节点执行信息聚集。

Ik=G-1kNkI

Pu=∑Ki=1QkIi，u（2）

Ik表示时间点t处的第k跳邻域中的度归一化均值;其中Nk表示第k跳邻域集;Nki，j=1仅当节点i和j恰好相距k跳时，否则为0;Gk是Nk的度矩阵。

Pu表示节点u在时间点t处的空间嵌入，通过对距离节点u长达K跳的不同跳邻域集的归一化均值进行加权聚集计算后获得。其中Qk是可学习的权重参数，用来捕获时间点t处的第k跳邻域的影响，不同跳邻域的显式聚集嵌入有助于区分不同跳邻域节点的流量强度对目标节点的影响。

2.2 时间依赖性建模

为了捕获不同时间点图之间的时间依赖性，采用聚集较早时间点的时空嵌入来计算，Xu表示节点u在时间点t处的时间聚集依赖。计算方法如式（3）所示，其中Xu表示节点u在时间点i处的时间嵌入;Q是时间点i处的可学习权重;ReLU是神经网络的激活函数。

Xu=ReLU（∑t-1i=1（QXu）（3）

2.3 時空嵌入连接建模

把目标节点和节点u的时空嵌入连接起来，计算出节点u在时间点t处的时空嵌入，表示为Xu。计算方法如式（4）所示。

Xu=ReLUQyIu||Pu||Xu+M（4）

其中Qy是时间点t处的可学习权重参数;|表示向量拼接操作;而M表示时间点t处的位置编码。在式（4）中，时间点t处的时间嵌入Xu捕获了从第1个时间点到t-1个时间点的交通流量时间依赖性，而空间嵌入Pu捕获了节点u的不同跳邻域的信息。另外，通过将时间点t处的位置编码值合并到节点嵌入中，还可以保留交通数据的周期性信息。交通数据的周期性特点又可以分类为每日模式、每周模式、每月模式等，大多数研究人员主要关注每日模式下的交通数据，在本文中采用两种不同的模型，即当天模型和历史模型，从而实现更有效的学习交通模式。

在历史模型中，设定最近a天，节点u在时间点t处的历史交通特征表示为Ihu∈Ra，本文设置a=7来获取一周交通数据的特征。当天模型仅需考虑当天时间点t的交通流量，使用Icu∈R来表示当天交通特征。在加入历史模型和当天模型的数据后，最终的时空嵌入连接如式（5）所示。

XXFu=X<1>Hu||…||XHu||X<1>Cu||…||XCu

XFu=QF·XXFu（5）

式中：XHu和XCu分别表示节点u在时间点t处的历史模型和当天模型下的时空嵌入;QF为可学习权重参数。

3 实验结果分析

为了证明本文提出的模型的有效性，使用三个公开可用的美国公路交通数据集PeMSD4、PeMSD7和PeMSD8进行了实验。实验机器是Windows10计算机（Intel Core i7-9 700处理器，内存16 G），实验软件使用Python3.9和深度学习框架MXNet1.5。为了报告不同模型之间的性能比较，选择平均绝对误差（MAE），均方根误差（RMSE）和平均绝对百分比误差（MAPE）作为评估指标。实验结果如表1所示。

在表1中很容易观察到，在PeMSD4、PeMSD7和PeMSD8三个评估指标的预测中，本文的模型均优于另外两种模型。显然，通过提出的时空图神经网络嵌入方案，能够更准确地捕获复杂的时空关系，从而取得了较好的性能。

4 结语

本文提出的时空嵌入模型可以汇总不同节点的空间相互关系，通过加权时空聚集方式获取时间相关性，提高了交通流量周期性预测的效率和准确率。由于测试数据集只包含流量数据，没有考虑外部因素，实际的交通数据集还应包括交通肇事、道路施工、大型活动、极端天气等，因此实验结果仅从单一维度进行测试和验证，后续需要结合多维数据集进行实验。

[1]徐冰冰，岑科廷，黄俊杰，等.图卷积神经网络综述[J].计算机学报，2020，43（5）：755-780.

[2]闫 旭，范晓亮，郑传潘，等.基于图卷积神经网络的城市交通态势预测算法[J].浙江大学学报（工学版），2020，54（6）：1 147-1 155.

[3]洪照雄.基于多图神经网络的城市交通流预测方法[D].杭州：浙江工业大学，2020.

[4]W.Hamilton，Z.Ying，J.Leskovec.Inductive representation learning onlarge graphs[C].Advances in neural information processing systems，2017.

[5]冯 宁，郭晟楠，宋 超，等.面向交通流量预测的多组件时空图卷积网络[J].软件学报，2019，30（3）：759-769.

[6]宋 超.时空网络上的图卷积模型及其应用研究[D].北京：北京交通大学，2020.

[7]荣 斌，武志昊，刘晓辉，等.基于时空多图卷积网络的交通站点流量预测[J].计算机工程，2020，46（5）：26-33.

[8]金仲明.基于时空图神经网络的交通预测[J].软件和集成电路，2019（7）：36-37.