考虑风光出力不确定性与相关性的混合电价机制设计

2021-11-02付文杰杨伯青黄莉李化

南方电网技术 2021年9期

付文杰，杨伯青，黄莉，李化

(1. 国网河北省电力有限公司保定供电分公司，河北保定071000；2. 东南大学，南京210096；3.国电南瑞南京控制系统有限公司，南京211100)

0 引言

2020年，国家电网公司发布了《国家电网公司2020年改革攻坚重组重点工作安排(2020年第8号)》(简称“8号文”)，将用户电价降低和输配电价改革作为电网改革攻坚的重点工作。售电公司通过价格和激励两种手段，可以引导用户合理地改变消费模式，转移用电负荷[1 - 2]。合理的电价机制可以让用户自发地将用电量从电价高的时段转移到电价低的时段，从而优化用电曲线，平抑峰谷差[3 - 4]。

电价机制影响着用户和售电公司两方的利益，合理的电价机制应该在保证售电公司的利益下，提高用户的满意度和可接受程度。目前很多省份已经试行分时电价，但是仍有不合理之处，如何完善电价机制，具有重要的研究意义。

文献[5]分析了电力用户分时电价的定价原则，并且提出了不同时段制定不同电价的分时电价对负荷曲线、用户电费的有利影响。文献[6 - 7]建立了需求响应的模型，分析了高峰时段和低谷时段电价对用户用电的影响，指出需求响应不仅可以缩短高峰时间，还可以为用户带来更多的利润。文献[8]提出了电力市场中能反映每小时甚至更短时间内电价变化的实时电价的定价原则和可行性。文献[9]分析了固定电价、实时电价、分时电价等几种定价策略的特点，提出了理想化的实时电价过于复杂，用户较难接受，缺乏一定的可操作性。文献[10]以供电商购买出售电价的效用最大为目标，建立了基于实时电价考虑电价成本、电价收入和风险的决策模型，但是此类常见的电价优化模型中，往往仅考虑到售电公司的利益，8号文中将用户电价降低作为改革的重点工作，可见用户侧的满意程度也应该在电价机制模型中作为重点考虑的因素。

文献[11]计算了电力价格弹性矩阵，以峰负荷及峰谷负荷差都最小为目标，建立了分时电价的多目标优化模型，但是电网模型中未考虑到光伏、风电等可再生能源接入的影响。近年来，以风光为代表的新能源发电逐渐向用户侧发展，用户电价降低和输配电价改革给新能源发电带来了新的机会。但是风电和光伏由于受天气的影响，出力较不稳定。文献[12]分析了近50年来多个地方太阳辐射与风速、湿度等气象因素的关系，指出不同地方太阳辐射与风速的相关性不同。文献[13]考虑了风、光出力的不确定性，基于峰谷分时电价，建立了配电网重构模型，但是模型中的电价机制不够合理，风光出力的相关性也未考虑。

因此，本文以售电公司为研究对象，提出了一种考虑风光出力不确定性与相关性的混合电价机制。首先提出了基于分时电价与实时电价的混合电价机制，该方法有效地结合了两种电价的优点，考虑到了用户的可接受性；其次考虑了光伏、风电为代表的可再生能源发电不确定性与相关性，采用拉丁超立方采样法对其出力进行分层采样和相关性控制；最后，以混合电价机制为基础，以售电公司的利润最大为目标，进行优化计算。以IEEE 33节点系统作为算例，将混合电价机制与分时、实时电价机制进行对比，验证分析了混合电价机制可以兼顾售电公司的利益和用户的满意度，是一种较为合理的定价机制，同时分析了风光出力不确定性与相关性的影响。

1 零售电价机制

1.1常用的电价机制

传统的固定电价机制无法达到优化用电曲线的目的。为了改善负荷用电曲线，实现削峰填谷，需要实施合理的零售电价的电价机制。为了引导用户优化用电行为，一般在用电高峰时段提高电价，用电低谷时段降低电价。电价的定价原则可分为5大类：经济效率、公平性、收入稳定性、支付稳定性和用户满意度。一般来说，一种合理的电价机制应该尽量多地符合上述每项原则。显然传统的固定电价机制已经不能满足上述的原则。目前常用的电价机制的特点如表1所示。

表1 常用的电价机制的特点Tab.1 Characteristics of common electric pricing mechanism

1.2 混合电价机制

除了上述方法外，文献[15]提出可以将不同的电价机制结合起来，分别提取不同电价机制的优点。高峰用电往往伴随着电力供应紧张、用电负荷过大等问题，在高峰时期采用实时电价方式不仅可以较为精确地反映当时的用电情况，而且可以针对性地引导用户减少或者转移用电负荷，从而优化用电方式。而在其他时段，没有电力供应不足问题，此时不需要精确却复杂的实时电价，用分时电价即可。因此本文采用了高峰时段使用实时电价，其他时段使用分时电价的混合电价机制。如图1所示，混合电价机制是在低谷时段和平常时段使用分时电价，在高峰时段使用实时电价的方法。

假设分时电价高峰时段的集合为φP，低谷时段的集合为φV。则分时电价ρTOU可以表示为：

(1)

式中：ρV为低谷时段的电价；ρP为高峰时段的电价。

图1 不同电价机制的定价原理Fig.1 Electricity pricing principles of different pricing methods

实时电价ρRT可以表示为：

ρRT=ρRT,t,t=1,2,…,24

(2)

式中ρRT,t为t时段的实时电价。

因此混合电价ρD可以表示为：

(3)

2 考虑风光相关性的采样策略

2.1 风光出力的相关性

以风力、光伏为代表的可再生能源有效地缓解了供需矛盾，但是由于风力、光伏受天气因素的影响较大，风力发电、光伏发电都具有一定的不确定性[16]。同一片区域的风力和光伏都受到该区域气象因素的影响，因此出力有着一定的相关性[12]。不考虑相关性的样本无法反映真实的出力情况，由采样得到的优化结果也具有一定的误差。

为了反映风电和光伏的不确定性与相关性，本文采用拉丁超立方采样法对风力、光伏出力这个随机变量进行采样和相关性控制。该方法的基本流程如图2所示。首先，通过大量的光伏和风电的历史数据，计算光伏和风电的相关性，得到相关系数矩阵；其次，在光伏和风电出力的分布曲线上进行分层采样；最后对光伏和风电出力的样本进行相关性控制，使得样本之间的相关性满足历史数据计算的相关系数，从而得到风光出力的样本矩阵。

图2 反映风光出力相关性的采样流程Fig.2 Sampling process reflecting the correlation of wind and solar power output

2.2 风光出力分层采样

假设在每个时间段内，光照强度服从Beta分布，风速服从Weibull分布，对光照强度和风速通过相应变换即可得到相应的光伏和风电出力。采用拉丁超立方样法对光照强度和风速进行采样。拉丁超立方采样法的核心思想的“分层采样”，从而让样本点均匀地分布在随机变量的分布曲线上[17]。相较于蒙特卡洛采样，该方法可以有效地改善样本堆积、分布不均的现象。

1)累积分布函数Z的取值范围为[0,1]，将其分为相同的L等份，各区间内依次随机抽取1个值；

3)假设a为0～1上的随机数，第l个区间抽取的采样值r1如式(4)所示。

(4)

按照上述步骤，即可得到光照强度的N个采样值。重复上述步骤，将Beta分布换成Weibull分布便可以得到风速的N个采样值。通过变换，即可得到某时间段内，一个光伏和一个风电出力组成的2行N列的样本矩阵为Rpw。

2.3 风光出力相关性控制

为了反映变量样本之间的相关性，可以采用相关系数矩阵。假设各变量之间的通过历史数据分析得到实际的相关系数矩阵是Preal，采样得到的样本值相关性是一般不等于Preal，无法反映实际的相关性，因此需要对样本的相关性进行变换。

本文采用Spearman秩相关系数来反映相关性，Spearman秩相关系数，用样本顺序代替样本值，可以反映随机变量为任何分布的相关性。相关性变换的相应步骤如下：

按2.1节得到Rpw，生成与Rpw规模相同的随机顺序矩阵S。对S的相关系数矩阵进行Cholesky分解，得下三角矩阵L；

为了让Rpw1的相关性满足Preal，对Preal进行Cholesky分解得到下三角矩阵Lreal；

对每个时间段的光伏和风电出力进行相应的采样和相关性控制，即可得到一天内光伏和风电出力所有的样本矩阵。

3 优化决策模型

3.1 优化模型

售电公司中的用户可以通过改变他们的用电行为，参与需求响应达到减少用电成本的目的。在这一节中，考虑到价格的灵活性和需求分布，式(5)为在时段t内用户D的需求响应经济模型[18]。

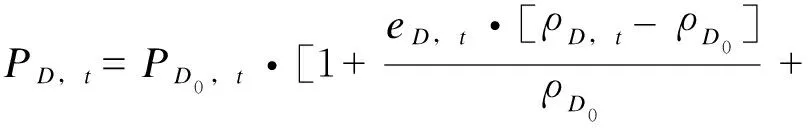
(5)

式中：t、h均为一天中的各个时段；PD0,t、PD,t分别为参与需求响应前后在t时段的总有功负荷；eD,t为用户在t时段的自弹性系数；eD,i,t,h为用户在t时段与h时段的交叉弹性系数；ρD0为对用户制定的固定电价；ρD,t为t时段对用户D制定的混合电价。

优化决策目标函数是使售电公司利润最大化，即等于收入和成本的差值最大。其中成本包括分布式电源的发电成本、向电力批发市场(即上级电网)购买电力的成本和风电、光伏的发电成本。收入包括出售给用户电量获得的电费与出售给电力批发市场得到的费用。目标函数如式(6)所示。

(6)

式中Rt、Ct分别为时段t的收入和成本。收入和成本如式(7)—(8)所示。

Rt=PD,t·t·ρD,t-PGSP,t·t·ρGSP,t

(7)

(8)

(9)

式中：PGSP,t为在t时段与电网交换的功率，该变量的正负值分别表示售电公司从电网购买和出售；ρGSP,t为t时段电力批发市场的价格；CDG,O,t为t时段分布式电源的运行成本；CDG,U,t为节点i分布式电源的启动成本；CDG,D,t为节点i分布式电源的关机成本；PDG,t为t时段分布式电源的发电功率；LDG,t为分布式电源机组运行状态的二进制决策变量，1表示运行，0表示关闭；MDG,t为分布式电源机组启动的二进制决策变量，1表示开启，0表示关闭；NDG,t分布式电源机组关闭的二进制决策变量，1表示关闭，0表示关闭；CWT,t、CPV,t分别为风电、光伏的发电成本，PWT,t、PPV,t为t时段风电和光伏的发电功率；t为t时段的总时长。

3.2 约束条件

本文的优化中考虑的约束包括3类：1)电网有功无功潮流约束；2)功率平衡约束；3)分布式电源的约束。

3.2.1 有功无功潮流约束

电网中的电压和功率分布必须满足潮流方程，潮流方程如式(10)所示。

(10)

式中：PG,i,t、QG,i,t分别为在t时段节点i总的有功出力和无功出力；PD,i,t、QD,i,t在t时段节点i有功负荷和无功负荷；Ui,t为t时段节点i的电压；Gij,t、Bij,t、δij,t分别为t时段节点i与节点j之间的电导、电纳及相角差；n为节点数量。

在上述等式中，PG,i,t、QG,i,t的计算如式(11)—(12)所示。

PG,i,t=PGSP,i,t+PDG,i,t+PWT,i,t+PPV,i,t

(11)

QG,i,t=QGSP,i,t+QDG,i,t+QWT,i,t+QPV,i,t

(12)

式中：QGSP,i,t为t时段与电网之间的无功功率交换量；QDG,i,t、QWT,i,t、QPV,i,t分别为t时段节点i分布式电源、风电、光伏产生的无功功率。

(13)

式中：Ui,max、Ui,min分别为节点i电压的上下限，每个节点的电压应该满足上下限的约束，不超过10%。同时售电公司与上级电网进行电力交易时不能超过电网最大的输出/输入功率PGSP,max。

3.2.2 功率平衡约束

总的有功功率、无功功率等于各节点的有功功率、无功功率之和。具体如式(14)—(15)所示。

(14)

(15)

式中：PPV,t,i、QPV,t,i分别为节点i的光伏有功功率和无功功率；PWT,t,iQWT,t,i分别为节点i的风电有功功率和无功功率；Ploss,t为t时段总有功损耗；Qloss,t为总无功损耗。

3.2.3 分布式电源约束

PDG,min,i≤PDG,t,i≤PDG,max,i

(16)

PDG,t+1,i-PDG,t,i≤PDG,U,i

(17)

PDG,t,i-PDG,t+1,i≤PDG,D,i

(18)

式中：PDG,max,i、PDG,min,i分别为节点i分布式发电机组的功率上限和下限；PDG,U,i、PDG,D,i为一个时间段内分布式发电功率可以上升或下降的最大速率。最大上升和下降速率分别取15%和10%。

4 算例

4.1 系统及参数介绍

本文以IEEE 33节点网架作进行算例分析。算例在MATLAB R2015a仿真平台上编程实现，1次优化模型求解时间约为15 s左右。假设售电公司的情况如下：1号节点(电网供电节点)通过1台容量为50 MVA的配电变压器连接至上级电网中，系统包含2台分布式电源(型涡轮发电机)、多个居民用户，1台光伏发电机和1台风力发电机。如图3所示：2台分布式电源分别连接在节点7和24上。此外，光伏和风机分别接在节点4和25。住宅用户分别连接在节点2—33。

图3 IEEE 33节点系统Fig.3 IEEE 33 node system

表2 分布式电源的参数Tab.2 Parameters of distributed power supply

4.2 不同电价机制的优化分析

将1 d分为峰谷平3个时间段，高峰时间段为07:00—10:00、17:00—19:00；低谷时间段为11:00— 16:00；平常时间段为1:00—6:00，20:00—24:00。不同时间段的价格弹性系数如表3所示。电力批发市场价格如图4所示。分别选择分时电价、实时电价和混合电价作为3种电价机制，对3种不同的电价机制进行优化分析。分时电价、实时电价、混合电价的定价如图5所示。不同电价机制的负荷曲线如图6所示。

图4 电力批发市场价格Fig.4 Wholesale market price of electric power

图5 不同电价机制的价格曲线Fig.5 Price curves of different pricing methods

图6 不同电价机制的负荷曲线Fig.6 Load curves of different pricing methods

表3 不同时段电价的弹性系数Tab.3 Elasticity coefficient of electricity price in different periods

分别计算分时、实时、混合定价3种算法的利润，取1 000组利润优化值的平均值作为最终的优化值。由1.1节可知，判断一个电价机制的效果，不仅需要考虑售电公司的利润，还应该考虑用户的满意度，因此本文还计算了用户的总电费。用户的电费越低，满意度越高。表4为3种算法的售电公司利润和用户总电费。可以发现本文提出的混合电价机制相比于其他2种方法，虽然利润相较于实时电价少了6 459元，但是用户的总电费比实时电价少了8 640元。而混合电价的利润和用户电费都要优于分时电价。所以综合比较，混合电价的效果比较好。

表4 3种零售电价机制的利润和电费Tab.4 Profit and tariff of three kinds of retail tariff

简单性指数也是判断一种电价机制的有效指标，代表每种定价方案对用户的复杂程度。一般来说，一种电价机制变化的越少，越符合用户的简单原则。显然，分时电价机制在价格上的变化较小，其简单性指数较高。实时电价机制最复杂。混合电价比分时电价机制略复杂，但比实时电价机制简单很多，是较优的一种选择。

4.3 风光出力特性的影响

1)不确定性的影响

为了研究风电和光伏的不确定性对优化模型的影响，图7给出了1 000次采样得到的1 000次利润的优化结果，可以发现，利润的波动性较大，风电和光伏的出力对利润有着较大的影响。如果不考虑风光出力的不确定性，会直接影响到对利润的判断，使得利润的估算过高或者过低。

为了将分时、实时和混合电价比较，与混合电价一样，计算分时、实时两种方法得到1 000次利润的优化结果。为了比较清楚地绘出对比图，随机选取50个样本下的优化值，如图8所示，可以看出风电和光伏的出力对3种算法的利润都有着类似的影响。

图7 混合电价1 000次采样的利润值Fig.7 Profit value of 1 000 samples of mixed electricity price

图8 不同电价机制的50次采样的利润值Fig.8 Profit value of 50 samples with different pricing methods

2)相关性的影响

不同地区光伏和风电的相关性呈现不同的关系，为了研究风电和光伏的相关性对优化模型的影响，将风电和光伏的相关系数分别设置为-0.8～0.8，以0.2为1个单位步长。光伏和风电之间的相关性经历了负相关-不相关-正相关。以混合电价为例，仍以1 000次采样得到的优化平均值作为利润平均值，以1 000次的采样得到的优化平均值计算标准差。表5为不同相关系数下的利润平均值，可以发现利润均值基本差不多，但是随着相关系数从负相关到正相关，利润均值有很小的可以忽略的增幅。

表5 相关系数对利润平均值的影响Tab.5 The influence of correlation coefficient on average profit

图9为相关系数为-0.8～0.8的利润的标准差，可以发现随着相关性从负相关-不相关-正相关，标准差在不断变大，利润的波动性在变大。这是因为当光伏和风电之间正相关时，特别是强正相关，如果光伏的发电量低或者高则风电的发电量也同样的低或者高，可再生能源的总体发电量会很高或者很低，波动性很大。相反地，当光伏和风电之间不相关甚至负相关时，光伏发电量高，风力很有可能处在发电量一般甚至很少的情况，可以与光伏互补，使得整个发电量水平不会过高或者过低，趋向平稳。相应的利润的波动性也会小一点。因此在优化模型中，为了更真实地反映利润的情况，需要考虑风电和光伏的相关性。