球型静力触探仪贯入双层土的困土效应

2021-11-02周小文肖自卫

哈尔滨工业大学学报 2021年11期

杨懿，周小文，周密，肖自卫

(1.亚热带建筑科学国家重点实验室(华南理工大学)，广州 510640；2.华南岩土工程研究院(华南理工大学)，广州 510640；3.中铁南方投资有限公司，广东深圳 518000)

海洋软土原位测试常采用静力触探。传统圆锥静力触探仪(cone penetrometer)在海洋软土中测得数据的精度随水深增加而降低[1]。新型全流静力触探仪(full-flow penetrometer)能有效减少超负荷应力造成的该测量误差。球型静力触探仪是全流静力触探的一种，其与软土接触面积较大，能获得更为精确的土体抗剪强度，且受土体刚度和应力各向异性影响较小，因此，被越来越多地应用于海洋岩土工程现场勘查和模型试验中[2-3]。

静力触探仪贯入属于岩土工程中的一个难点问题，针对球型静力触探仪的贯入，许多学者已开展了相应的研究工作。理论方面，李镜培等[4]基于修正剑桥模型推导了球孔扩张问题的半解析解；李林等[5-6]进一步推导了K0固结状态下该问题的弹塑性解析解并将其应用于静力触探，通过触探仪的测量数据预测了静压桩时变承载特性；陈浩华等[7]拓展建立了不排水条件下超固结黏土中球孔扩张的弹塑性解；Randolph等[8]采用极限分析上下限定理严格推导了塑性理论解。但理论解忽略了探杆和贯入速率的影响，且不能反映实际贯入的连续性。试验方面，Salgado等[9]基于标定罐试验研究了贯入速率对贯入阻力的影响；Dejong等[10]结合大量现场数据提出了测试规范和解释指南；Morton[11]通过离心试验研究了贯入过程土体破坏机制；年延凯等[12]取中国南海土进行室内循环贯入测试，提供了阻力系数的参考值。试验往往成本高昂、难以实现，数值模拟成为重要研究手段。采用传统的拉格朗日或欧拉有限元方法通常不易收敛，将两种方法结合有助于解决收敛问题。如Wang等[13]利用耦合拉格朗日-欧拉方法(CEL)成功模拟了全流静力触探仪在软黏土中的深层贯入，但CEL方法基于流体方法模拟土体特性，计算精度不足；范庆来等[14]使用任意拉格朗日-欧拉方法(ALE)分析了全流静力触探仪的贯入机制，但在土体扰动频繁情况下ALE方法的模拟效果欠佳；Zhou等[15]通过大变形有限元方法研究了杆轴对贯入阻力的影响，贯入过程网格形态保持良好。

然而，对静力触探仪贯入特性的研究主要集中于单层土条件，实际海洋工程中常见的层土地基情况相关研究较缺乏。由于层土地基中各层贯入阻力并非与该层土体强度独立对应，有必要探讨土层之间相互影响引起的贯入特性变化。陈刚等[16]认为CPT探头位于土层分界面时周围土体的变形可视作在另一均质土中的球孔扩张，提出了双层土的同心分层球孔扩张解； Walker等[17]利用数值模拟探讨了CPT锥尖阻力随土层厚度和土体性质的变化规律；Mo等[18]基于离心试验发现CPT的贯入阻力和土体变形规律主要取决于两层土的相对性质。而针对球型贯入仪的相关文献极少。Lee等[19]在砂土覆盖黏土的双层土地基离心试验中发现，上层砂土被困于球型探头底端并带入下层黏土中，产生了困土现象，这严重影响了下层土贯入阻力。困土现象在Hossain等[20]研究纺锤体基础的双层黏土地基离心试验中也被观察到。但目前还未见对困土效应的机理解释和深入研究。

针对球型静力触探仪的困土效应开展研究，采用改进的RITSS (remeshing and interpolation technique with small strain) 大变形有限元方法模拟触探仪在双层土地基中的贯入过程，探究困土效应的产生条件与机理，通过参数分析考察困土效应的影响因素，得到归一化困土尺寸，进一步提出修正困土效应的土体不排水抗剪强度计算公式，为球型静力触探仪在双层土地基中的应用提供参考。

1 研究方法

RITSS方法是1998年由Hu等[21]提出的一种大变形有限元数值分析方法，其基于连续小应变分析与周期性网格重构技术实现对大变形的模拟，本质上属于任意拉格朗日欧拉(ALE)方法，但在网格细分和变量映射时更具优势。RITSS方法的实现步骤可分为：1)生成初始网格；2)进行多步拉格朗日小应变分析；3)更新计算边界并重新划分网格；4)将场变量从旧网格插值映射到新网格；重复步骤2)至步骤4)直至达到所需位移条件。该方法能确保网格质量，适用于处理大变形问题，在国际上已得到了学术界的认可并在静力触探、纺锤形基础、加劲肋沉箱基础等海洋岩土贯入问题中得到了广泛应用[22-24]。

模拟球型静力触探仪贯入成层土时，材料线将在土层分界面附近发生间断。传统ALE方法的处理是将网格不断细化，直到无法再细化时计算中止；RITSS方法是基于线性插值进行动态网格划分，但需要预先获知材料线断裂位置和自由面位置。材料线间断次数与位置的组合可能情况有上百种，此时要动态更新材料边界异常困难。为此，在RITSS方法的基础上开发了轴对称情况下动态边界索引与网格分区管理功能和动态步长自适应功能。程序设计流程(见图1)如下。

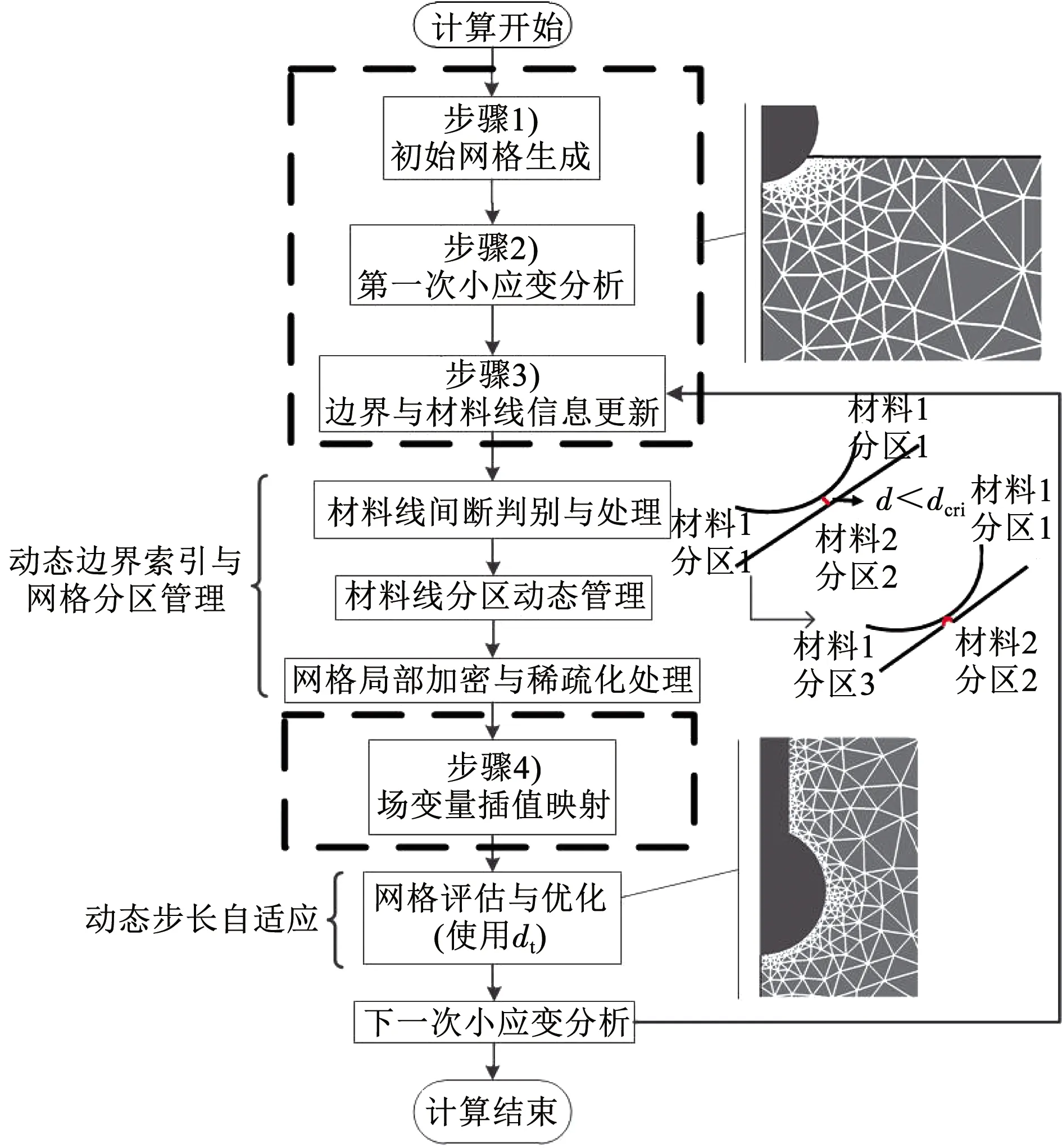
图1 球贯入双层土地基的RITSS程序设计流程

首先，执行RITSS方法的前3个步骤，根据更新后的边界和材料线信息识别各层土体所处位置。

其次，基于预设准则进行材料线间断判别与处理。本研究中处理准则设置为dcri=0.05hmin，其中dcri为临界位移，hmin为最小网格尺寸。当两条材料线或材料线与贯入仪之间的距离小于dcri时，认为两者相接触，自动断开材料线并进入分区动态管理。

再次，对重点关注的区域(球型探头附近)进行局部网格加密，在远离球型探头的区域使用相对稀疏的渐变过渡网格。

之后，执行RITSS方法的第4)步，并对新网格进行评估与优化。根据网格信息动态计算合适的贯入位移增量步(dt)，在保证精度的同时减少不必要的网格重划分次数，从而提高计算效率。

最后，进入下一次小应变分析，循环直至达到所需贯入深度时结束计算。

通过该改进的RITSS方法能有效解决球型静力触探仪贯入层土过程材料线间断和自由面捕捉的问题(这也是大变形模拟中的关键和难点)。

修水县不断增加对旅游发展的投入。当地根据优势资源着重计划、投资6亿元兜率寺、投资20亿元温泉度假旅游项目、投资2亿元宁红茶文化园、投资7亿元东浒寨旅游，并实行政策倾斜保障，将农业、林业、水利、交通、扶贫脱困、移民、新农村建设、文物保护等专项资金与旅游建设发展相结合，成立县旅游发展总公司，搭建科学高效的旅游融资平台，同时，县财政在安排2000万元文化旅游发展专项基金基础上，按当地财政增长比例和旅游发展情况，视情逐年递增，为旅游发展提供资金保障，为修水的旅游发展奠定深厚的基础。

2 模型建立

2.1 几何模型与材料参数

选用直径(D)为113 mm、杆轴直径(Dshaft)为36 mm、杆轴投影面与球截面面积比(a)为0.1的标准球型静力触探仪(见图2(a))，考虑上软下硬和上硬下软两种双层黏土地基条件(见图2(b))，其中上层土厚度为t、贯入深度(球底端到土体表面的距离)为din、上下两层土体的有效容重分别为γt′和γb′。

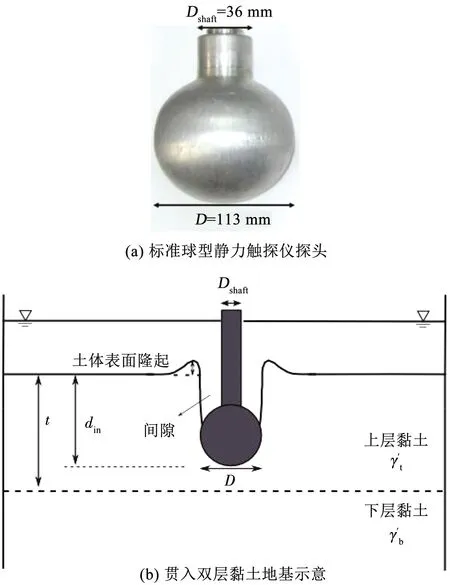
图2 球型静力触探仪及其贯入双层黏土地基示意

黏土的不排水抗剪强度可通过式(1)计算，即

(1)

式中：su为黏土不排水抗剪强度，qnet为净贯入阻力，Nb为稳定承载力系数。对于双层黏土，上层土不排水抗剪强度为sut，下层土不排水抗剪强度为sub。

2.2 模拟设置与本构关系

理想情况下球型静力触探仪贯入时几何、荷载和边界以中心轴对称，故简化为二维轴对称模型[8,25-26]。本研究分析域范围为18D× 18D，足以避免边界效应。探头嵌入土体约0.2D。下边界设置为固定约束，左右边界设置仅约束水平位移。球型静力触探仪与土体的接触界面使用弹塑性节点约束关系模拟[27]，界面上的极限摩擦力为αsu，其中α为球土接触面的摩擦因数。采用具有3个内部高斯点的六节点三角形网格，并在探头附近与土层分界线附近进行局部加密。典型网格如图3所示。

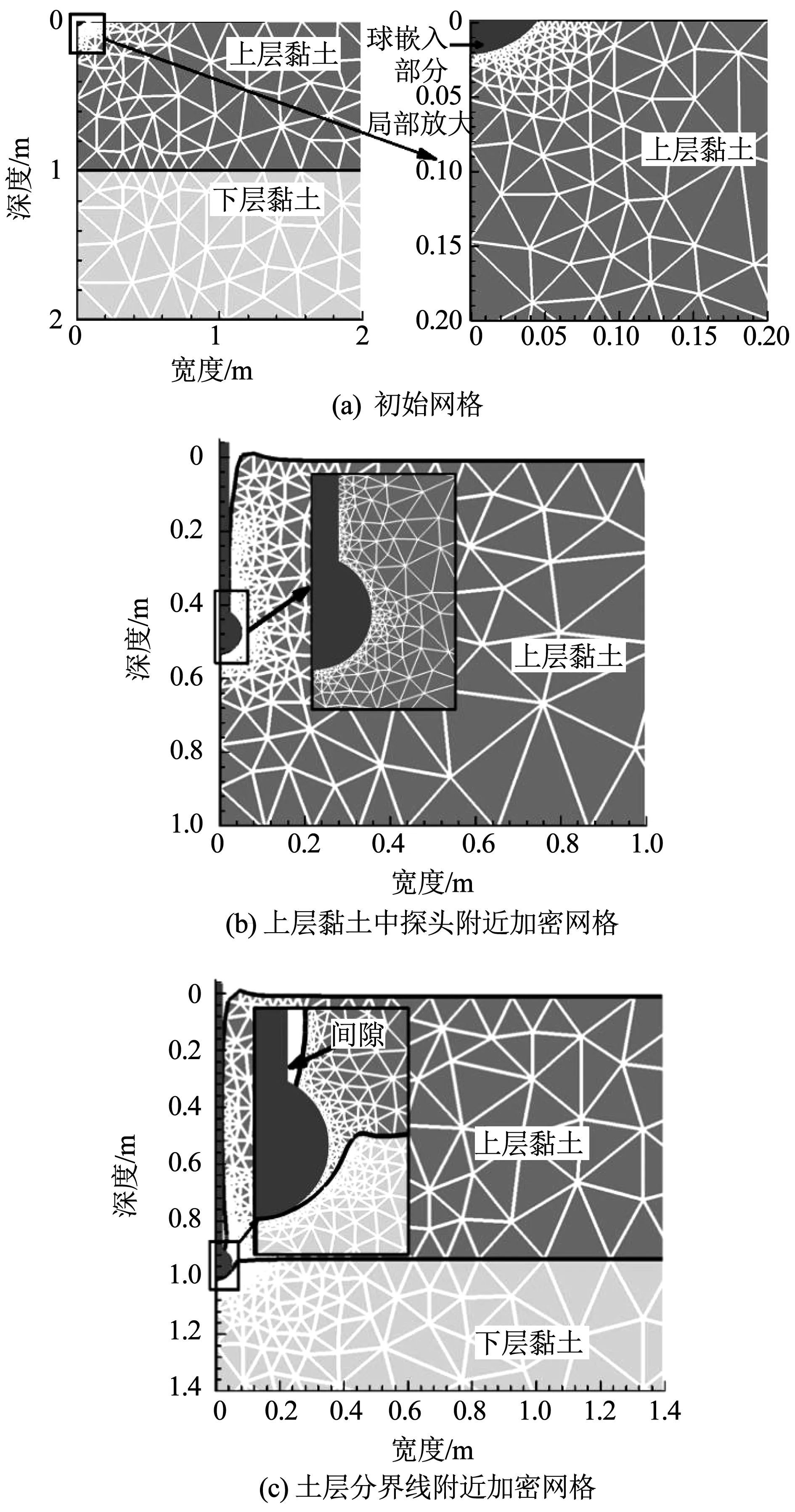
图3 球型静力触探仪贯入双层黏土地基的典型网格

将土体模拟为服从Tresca屈服准则的理想弹塑性模型。弹性参数包括杨氏模量(E)和泊松比(υ)，认为其与应力无关并在贯入过程中保持为恒定值；塑性参数为黏土的不排水抗剪强度(su)，其定义了屈服面的大小；摩擦角(φ)和剪胀角(ψ)表征破坏时的塑性响应。土体的刚度比(E/su)设定为中等刚度值500[28]。由于黏土渗透系数很小，贯入过程(标准贯入速率20 mm/s[10])中可不考虑土体的固结，即不固结不排水条件。设定υ=0.49、φ=0、ψ=0。采用White等[29]的方法将土体浮力的影响考虑在内。如图4所示，改变静止土压力系数(K0)，发现无论在单层土还是双层土中，归一化贯入阻力稳定值几乎不随K0的变化而变化，因此，地应力条件采用K0=1。基于现场试验数据与前人研究[30-34]选取其他计算参数，详见表1。

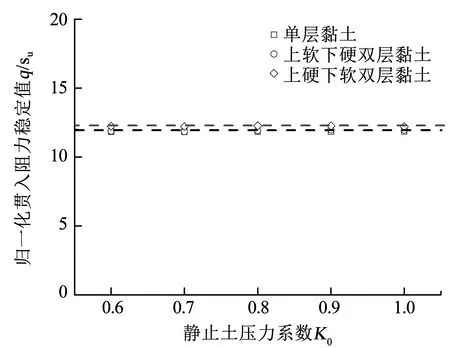
图4 静止土压力系数对归一化贯入阻力稳定值的影响

3 结果分析

3.1 数值模型的验证

为验证数值模型的可靠性，将大变形有限元分析结果(表1中组1、2)分别与塑性理论解[8]和离心试验[35]进行对比验证。如图5(a)所示，当球体完全光滑时(α=0)，稳定承载力系数(Nb)为10.98，当球体完全粗糙时(α=1)，稳定承载力系数(Nb)为15.20，均介于塑性理论解上下限。

如图5(b)所示，采用大变形有限元分析得到的土体不排水抗剪强度曲线与Zhou等[35]的离心试验数据非常接近，最终稳定值约为13.5 kPa。表明本研究所采用的RITSS方法能够较好地模拟球型静力触探仪的贯入问题。

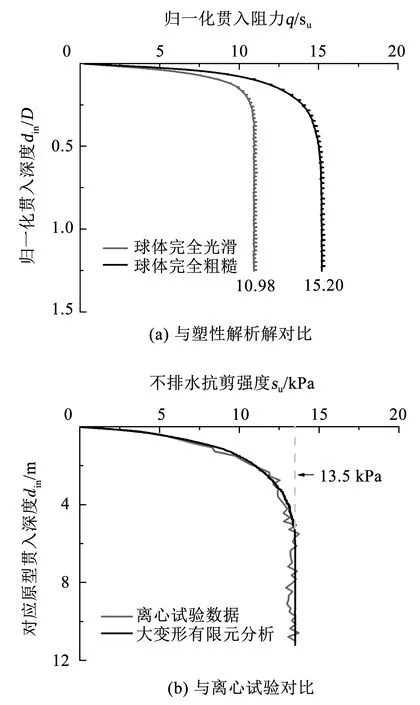
图5 大变形有限元数值结果的验证

3.2 土体流动机制分析

图6、7(表1中组3)显示了球型静力触探仪贯入双层黏土地基中的土体流动机制。在上软下硬的双层黏土地基中(图6)，土体流动机制大致分为3个阶段：

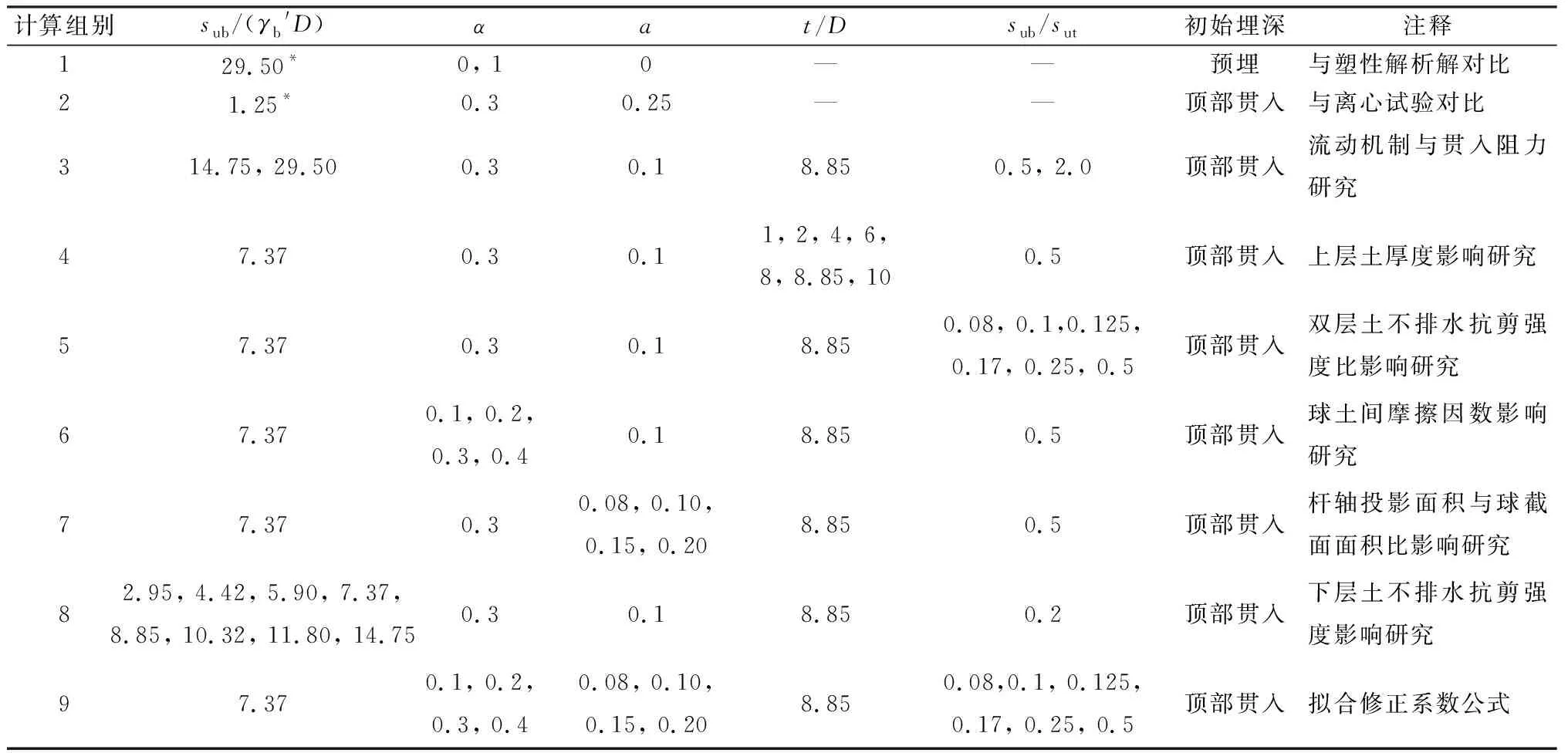
表1 大变形有限元分析计算汇总

2) 第2阶段。开始贯入下层硬土，土层分界线变形，球型探头周围上层软土受侧向挤压并逐渐被下层硬土替代(图6(c))。

3) 第3阶段。贯入下层土足够深度后，球型探头被回流的下层硬土完全包裹(图6(d))。此时土体流动机制与单层黏土的全流动机制一致，表明单层黏土的稳定承载力系数可用于土层分界过渡区之外的下层土。

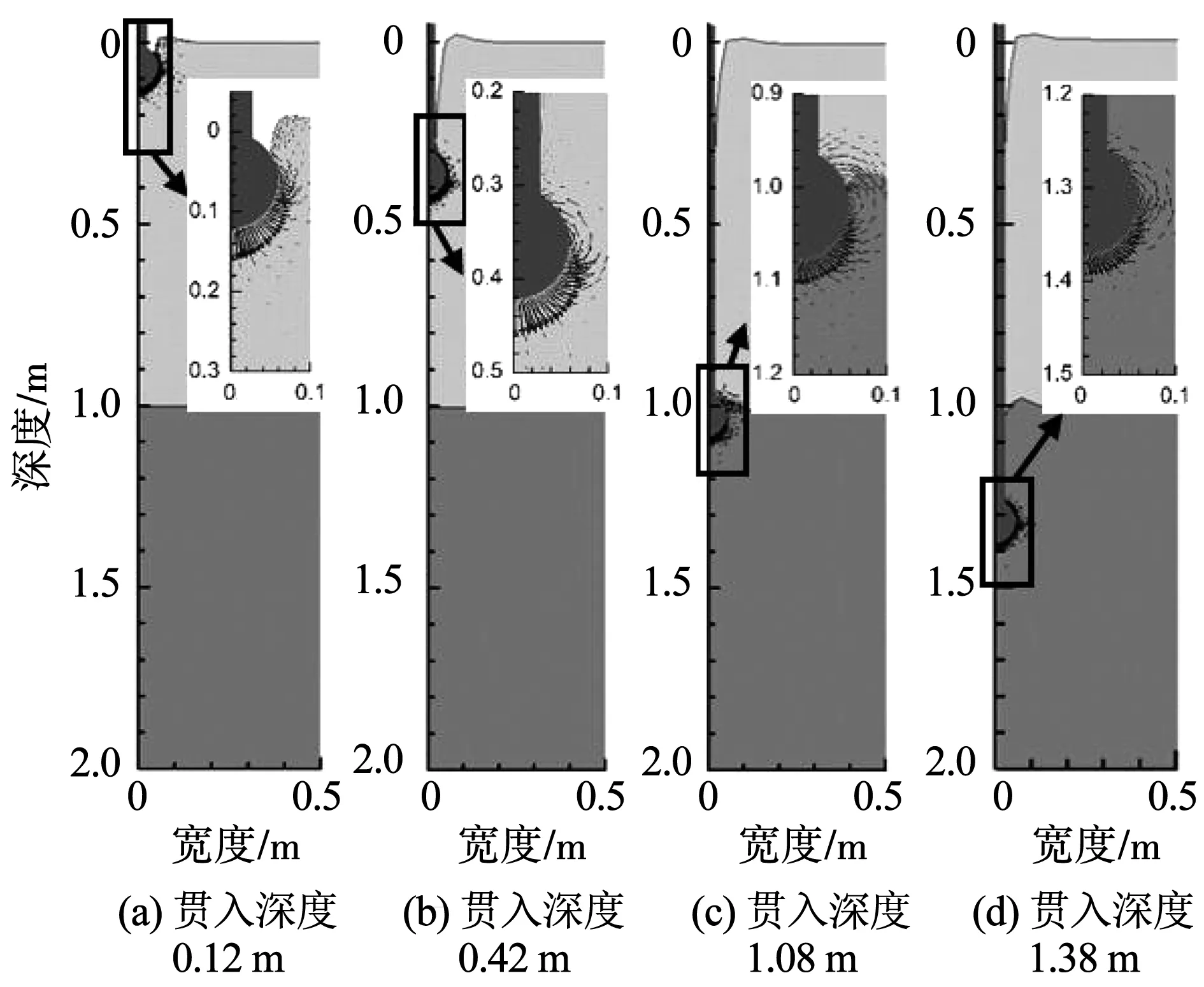
图6 贯入上软下硬双层黏土地基的土体流动机制

上硬下软的双层黏土地基中(图7)土体流动机制也可分为3个阶段：

1)第1阶段类似(图7(a))。但当上层土厚度不足以使土体形成完整环流场时，土体无法覆盖至球型探头顶端，导致与加载杆之间产生两个间隙(图7(b))。

2)第2阶段。贯入下层软土，土层分界线变形。上层土受侧向挤压时，由于相对较硬，无法被软土完全替代，部分截留于球型探头底端并随贯入进入下层土，开始出现困土(图7(c))。

3)第3阶段。贯入下层土足够深度后，困于球底端的硬土与上层土彻底分离，被回流的软土包裹并限制在探头底部，形成困土效应(图7(d))。此时，探头测得的下层软土贯入阻力受硬土影响而偏大。困土现象在Wang等[36]的离心试验中也被捕捉到。

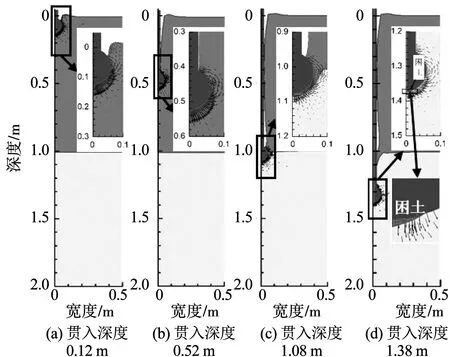
图7 贯入上硬下软双层黏土地基的土体流动机制

3.3 贯入阻力曲线分析

球型静力触探仪在双层黏土地基中的贯入阻力曲线如图8(表1中组3)所示，同等不排水抗剪强度下单层均质黏土的贯入阻力曲线也展示于图中以作比较。贯入阻力采用下层软土不排水抗剪强度进行归一化处理，贯入深度采用球型探头直径进行归一化处理。

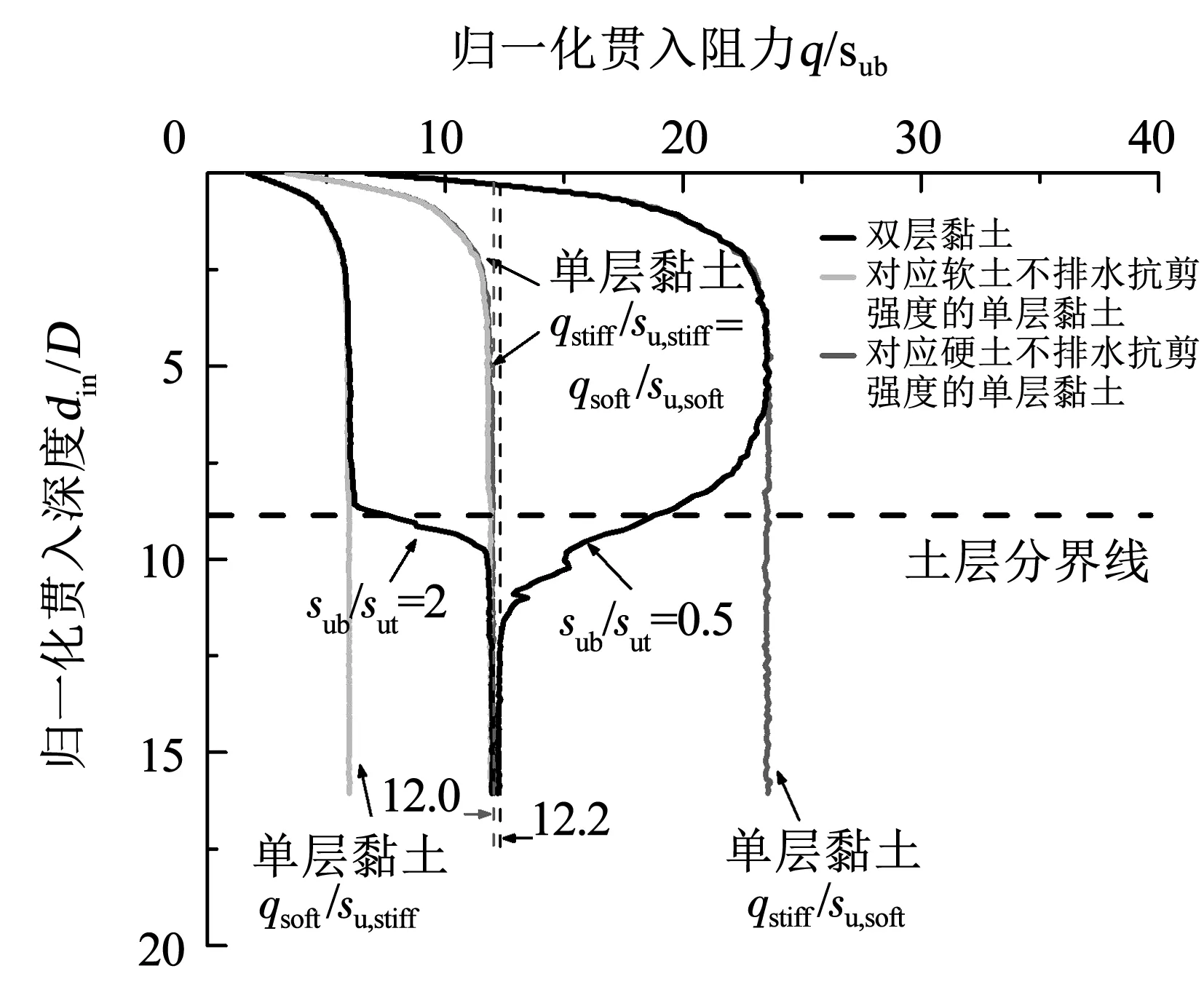
图8 贯入双层黏土地基的典型贯入阻力曲线

对于上软下硬的双层黏土地基，在土层分界线上方约1D距离之前，贯入阻力曲线与对应上层软土不排水抗剪强度的单层均质黏土的贯入阻力曲线(qsoft/su,stiff)重合；接近下层硬土时，土体归一化贯入阻力显著增大，在土层分界线下方约1.5D距离之后，下层硬土贯入阻力曲线与对应下层硬土不排水抗剪强度的单层均质黏土的贯入阻力曲线(qstiff/su,stiff)吻合，说明此时探头周围上层土已完全被下层土替代，探头测得的稳定贯入阻力即为下层硬土中实际贯入阻力，可使用式(1)计算土体不排水抗剪强度。

对于上硬下软的双层黏土地基，贯入阻力过渡区相较上软下硬的双层黏土地基明显增大，范围为土层分界线以上约3D和分界线以下约5D距离。下层软土中，由于困土效应的影响，稳定后的归一化贯入阻力与对应下层软土不排水抗剪强度的单层均质黏土(qsoft/su,soft)相比偏大。此情况下，经式(1)计算出的土体不排水抗剪强度值将偏大。

4 困土效应

4.1 产生机理

由前节分析发现，困土效应存在于上硬下软双层黏土地基中，不存在于上软下硬双层黏土地基中(如图6、7所示)。

球型静力触探仪贯入下层软土后，由于上层土不排水抗剪强度较大以及土体与探头之间存在摩擦接触，原先位于探头底部的硬土无法被软土挤压排开，而是随着贯入深度增加进入下层直至被软土完全包围。因此，探头底端接触土体实际为硬土，使得所测贯入阻力偏大。在上层硬土限制下，下层软土水平方向的流动加强，全流动机制不再是绕着球型探头的标准环流(即流线不再是接近圆形的轨迹)，土体流动不再沿球心上下对称，这种偏离也增大了贯入阻力。

4.2 参数分析

由机理分析可知，困土效应与土层相对强度和球土间摩擦因数直接相关。此外，上层土厚度、杆轴投影面与球截面面积比也影响着土体的流动机制与贯入阻力曲线。故参数分析考虑上层土厚度、土体强度、球土间摩擦因数、杆轴投影面与球截面面积比，得到球型静力触探仪贯入上硬下软双层黏土地基的结果如下。

1)上层土厚度与球体直径之比(t/D)的影响。图9(表1中组4)显示了上层土厚度与球体直径之比(t/D)在1～10时，归一化贯入阻力沿归一化贯入深度的变化情况。分别对应软土和硬土不排水抗剪强度的单层黏土(以t/D=0和t/D=∞表示)贯入阻力曲线也展示在图中。当t/D≤8时，上层硬土贯入阻力未达到对应单层黏土(t/D=∞)中的稳定值便受到下层软土影响而急剧减小。且t/D越大，下层软土的影响范围越大。但当上层土厚度(t)超过1 m时(t/D≥8.85)，上层硬土贯入阻力达到了稳定贯入阻力，全流动机制形成。下层软土中稳定承载力系数不随上层土厚度与球体直径之比(t/D)的改变而改变，都较对应单层黏土(t/D=0)增大约2%，说明上层土厚度对困土效应影响可忽略。

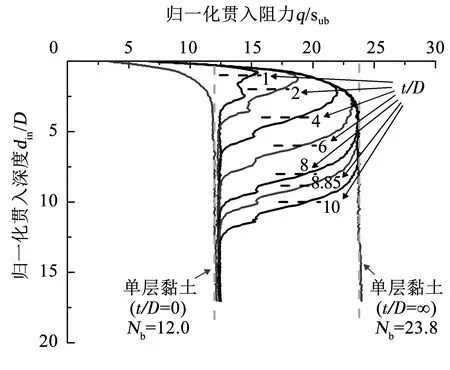
图9 上层土厚度不同时的贯入阻力曲线

2)下层土与上层土不排水抗剪强度比(sub/sut)的影响。固定下层土归一化不排水抗剪强度(sub/(γb′D)=7.37)、球土间摩擦因数(α=0.3)和上层土厚度与球体直径之比(t/D=8.85)，改变下层土与上层土不排水抗剪强度比(sub/sut取为0.08～0.5)，得到图10中的上硬下软双层黏土地基中贯入阻力曲线(表1中组5)。随着下层土与上层土不排水抗剪强度比(sub/sut)由0.08增大到0.5(即两层土间的不排水抗剪强度差值减小)，下层软土的稳定承载力系数(Nb)由20.0减小到12.2，逐渐接近单层均质黏土(t/D=0)中的值12.0。下层软土的影响范围随下层土与上层土不排水抗剪强度比(sub/sut)的增大而减小，说明两层土间相对强度差值的减小使得下层软土影响推迟，困土效应减弱。值得注意的是，当下层土不排水抗剪强度为上层土不排水抗剪强度的12.5倍(sub/sut=0.08)时，困土效应导致下层软土归一化贯入阻力稳定值相较单层黏土(t/D=0)情况偏大了66.7%。

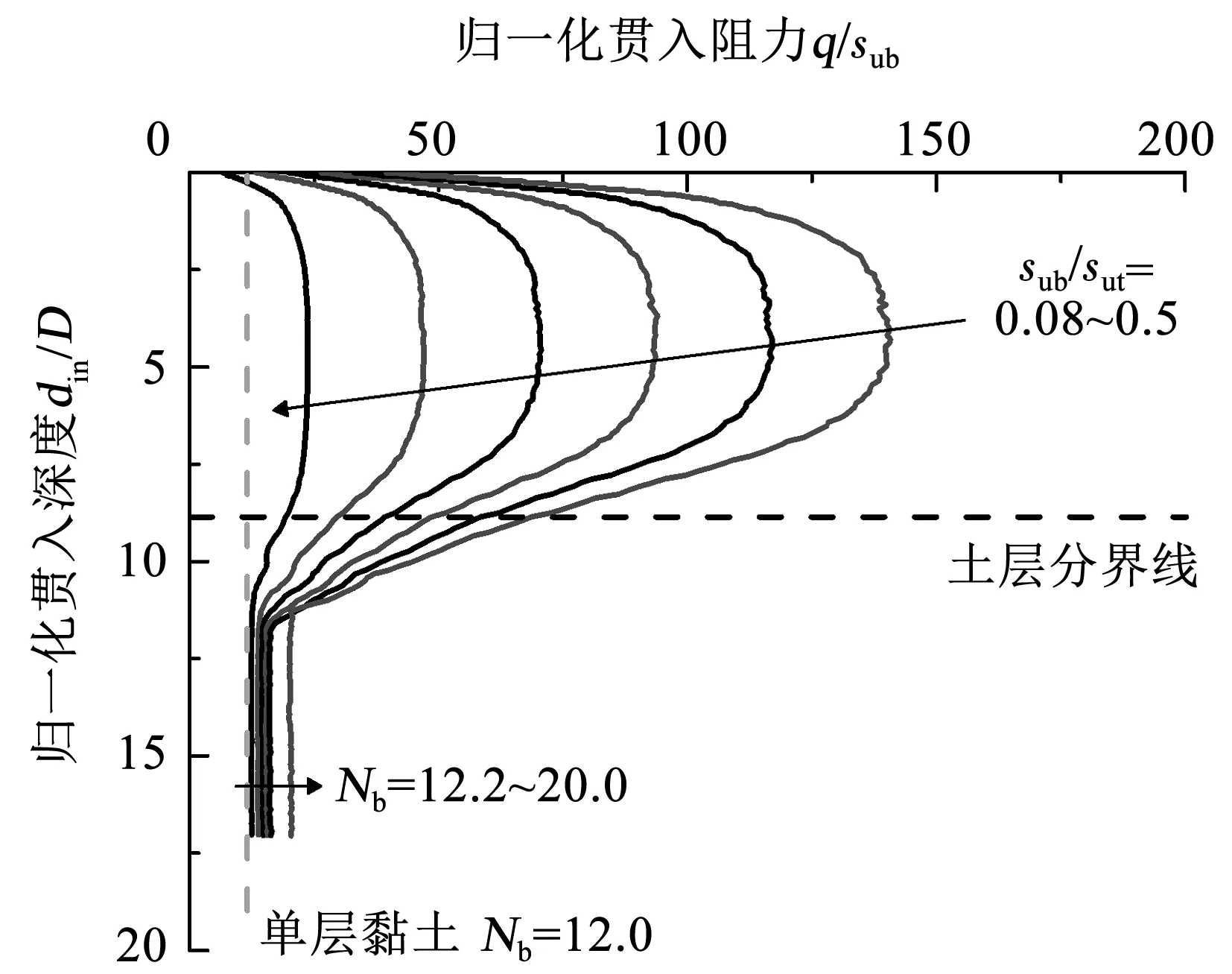
图10 双层土不排水抗剪强度比不同时的贯入阻力曲线

3)球土间摩擦因数(α)的影响。基于现场试验经验值选择球土间摩擦因数为0.1～0.4进行研究，其他参数固定，结果如图11(表1中组6)所示。球土间摩擦因数(α)对归一化贯入阻力曲线影响显著，下层软土中稳定承载力随着球土间摩擦因数(α)的增大而增大，与单层黏土(t/D=0)的差别也逐渐增大。说明困土效应随着球土间摩擦因数的增大而增强。

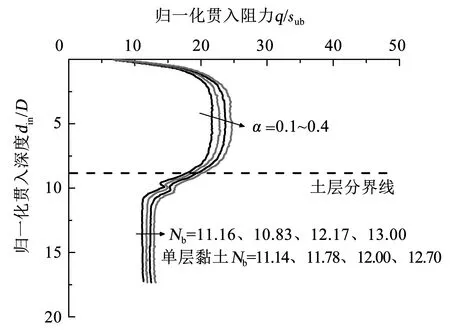
图11 球土间摩擦因数不同时的贯入阻力曲线

4)杆轴投影面与球截面面积比(a)的影响。考虑实际工程中球贯入仪不同杆轴比(a)的主要范围为0.08～0.20[10,37]，开展a的影响特性研究，计算结果如图12所示(表1中组7)。可以看出，贯入阻力曲线在上层硬土中影响较小，下层土中则有一定的影响。杆轴投影面与球截面面积比(a)的增大引起贯入阻力稳定值减小，对困土效应有一定影响，但相对土体强度比和摩擦因数影响较小。

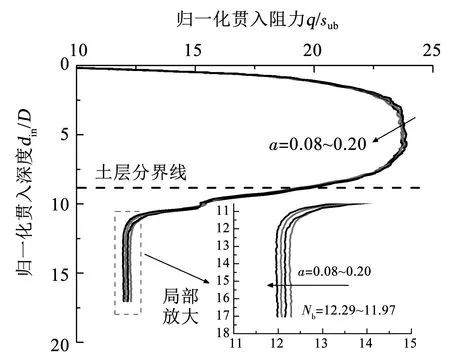
图12 杆轴投影面与球截面面积比不同时的贯入阻力曲线

5)下层土归一化不排水抗剪强度(sub/(γb′D))的影响。单层黏土中，土体的归一化不排水抗剪强度对土体流动机制有影响。现改变下层土归一化不排水抗剪强度(范围2.95～14.75)，固定下层土与上层土不排水抗剪强度比(sub/sut=0.2)，讨论下层土不排水抗剪强度的影响，计算结果展示在图13(表1

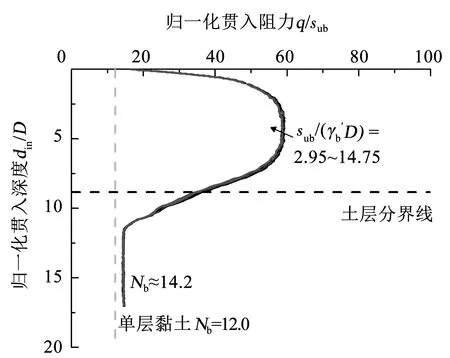
图13 下层土不排水抗剪强度不同时的贯入阻力曲线

中组8)中。可以看出，下层土中贯入阻力曲线近乎重合，下层土的归一化不排水抗剪强度的变化未引起下层土的归一化贯入阻力变化。进一步证明困土效应是受两层土之间的相对强度而非下层土不排水抗剪强度影响。

4.3 困土尺寸

以归一化困土厚度(Hplug/D)和归一化困土宽度(Wplug/D)量化表征困土效应。参数分析中下层土与上层土不排水抗剪强度比和球土间摩擦因数的影响如图14所示。

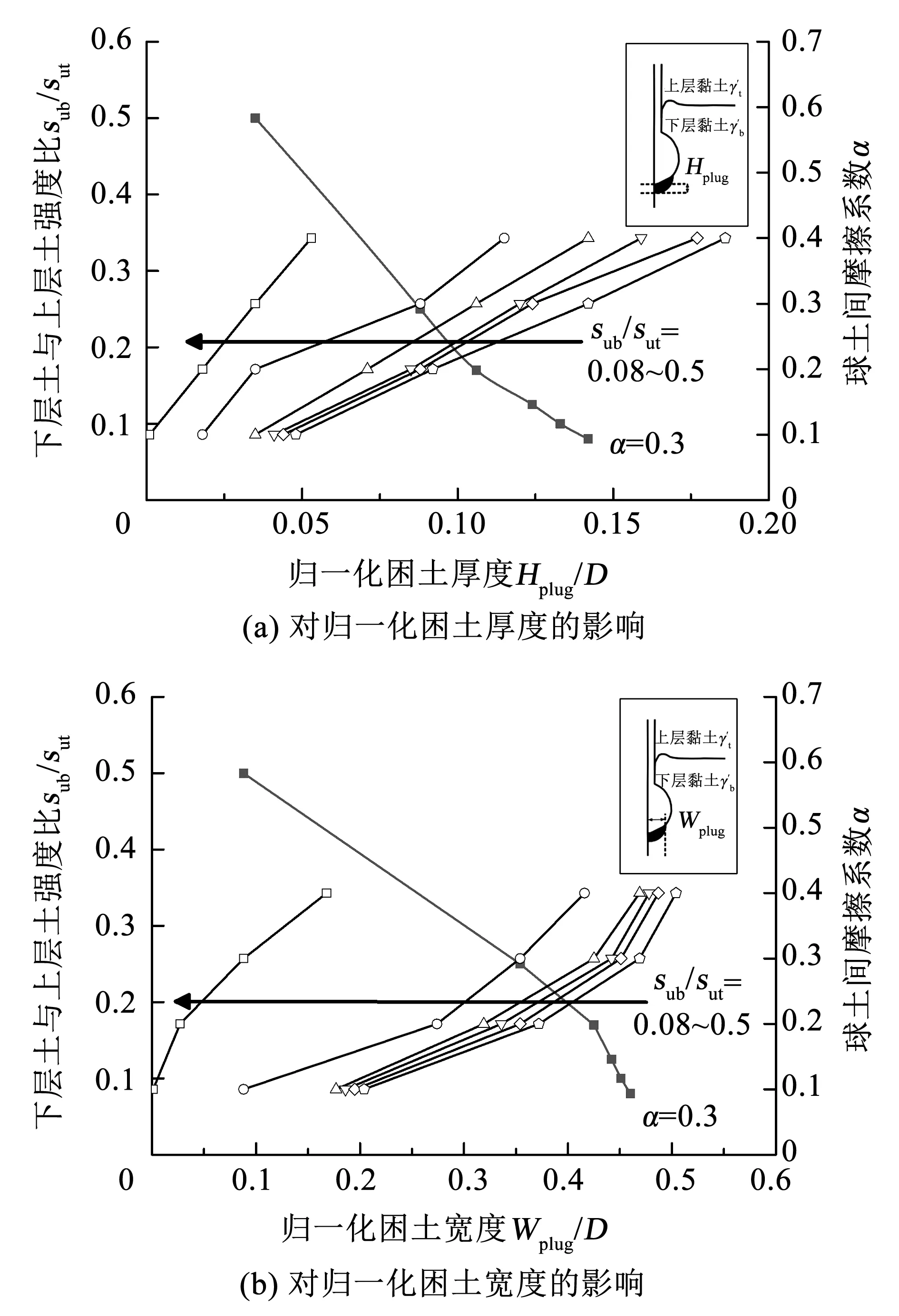
图14 强度比和摩擦因数对归一化困土尺寸的影响

随着下层土与上层土的不排水抗剪强度比(sub/sut)增大(即两层土间的不排水抗剪强度差值减小)，归一化困土厚度(Hplug/D)和归一化困土宽度(Wplug/D)均减小，困土效应减弱。上层硬土不排水抗剪强度恒定，下层土不排水抗剪强度较小时，硬土将更自由地陷入软土中，从而增大困土尺寸，加强困土效应。固定下层软土不排水抗剪强度时，在不排水抗剪强度较大的上层硬土中，土体回流较为缓慢，硬土竖直向下流动相对增多，使得困土尺寸增大。当同时改变上下两层土体强度但保持比值不变时，困土尺寸不变。

归一化困土厚度(Hplug/D)和归一化困土宽度(Wplug/D)均随球土间摩擦因数(α)的增大而增大。这是因为探头较粗糙时土体更容易滞留在周围。

在sub/sut取0.08～0.5、α取0.1～0.4进行研究，对于标准球型贯入仪(a=0.1)，困土厚度变化为0～0.20D，困土宽度变化范围较大，为0～0.50D。