Efficient Probabilistic Load Flow Calculation Considering Vine Copula-Based Dependence Structure of Renewable Energy Generation

MA Hongyan(马洪艳), WANG Han(王 晗), XU Xiaoyuan(徐潇源), YAN Zheng(严 正), MAO Guijiang(毛贵江)

1 College of Information Science and Technology, Donghua University, Shanghai 200051, China

2 Key Laboratory of Control of Power Transmission and Conversion(Shanghai Jiao Tong University), Ministry of Education, Shanghai 200240, China

3 State Grid Quzhou Power Supply Company, Quzhou 324000, China

Abstract: Correlations among random variables make significant impacts on probabilistic load flow(PLF) calculation results. In the existing studies, correlation coefficients or Gaussian copula are usually used to model the correlations, while vine copula, which describes the complex dependence structure(DS) of random variables, is seldom discussed since it brings in much heavier computational burdens. To overcome this problem, this paper proposes an efficient PLF method considering input random variables with complex DS. Specifically, the Rosenblatt transformation(RT) is used to transform vine copula-based correlated variables into independent ones; and then the sparse polynomial chaos expansion(SPCE) evaluates output random variables of PLF calculation. The effectiveness of the proposed method is verified using the IEEE 123-bus system.

Key words: probabilistic load flow(PLF); vine copula; sparse polynomial chaos expansion (SPCE); Rosenblatt transformation(RT)

Introduction

Probabilistic load flow(PLF) is an effective tool to analyze power flow under uncertainties, in which the correlations of input random variables significantly affect PLF results. The uncertainties include variable renewable energy generation and load demands[1]. Meanwhile, Monte Carlo simulation(MCS), point estimate methods and cumulant methods are widely utilized in PLF analysis. MCS is usually the benchmark method which can obtain accurate PLF results with heavy computation burden[2-4]. The point estimate method and the cumulant method can improve the efficiency of PLF calculation but impair the accuracy[5-6]. Recently, polynomial chaos expansion-based surrogate model is used to obtain the PLF calculation results, which is regarded as an effective method to balance the computation burden and accuracy[7]. Furthermore, in the existing literature, correlation coefficients or Gaussian copula are usually used to describe correlations between input random variables. In Refs. [8-10], correlation coefficients are used to depict the correlated renewable energy generation. In Ref. [11], the Gaussian copula is applied to model stochastic dependence in power system. However, these two methods fail to consider the complex dependence structure(DS) such as tail dependence and asymmetric DS, which are exhibited in the generation power of adjacent renewable energy units. Neglecting the complex DS will underestimate the risk of power system operation. Recently, the vine copula has been introduced to model the complex DS in power systems, by establishing the joint probability distribution of multiple variables with pair-copula constructions[12]. Nevertheless, the computational burdens of the vine copula-based PLF are extremely heavy, because input samples are generated from the joint probability distribution and then the PLF problem is solved using MCS[13]. Hence, the motivations of this paper include two aspects.(1) The impacts of intermittent renewable energy generation on the operation states of distribution network are extremely significant. How to evaluate those impacts?(2) The correlation among the generation power of adjacent renewable energy units are complex. How to realize efficient PLF calculation considering the complex DS?

The contributions of this paper are summarized as follows. Considering vine copula-based DS, this paper proposes an efficient PLF calculation method based on the Rosenblatt transformation(RT) and sparse polynomial chaos expansion(SPCE). RT decouples correlated input random variables into independent ones, and then SPCE solves PLF with independent variables efficiently. The effectiveness of the proposed method is verified using the IEEE 123-bus system.

1 DS of Random Variables

1.1 Correlation coefficient and Gaussian copula

The correlation coefficients, such as linear correlation and rank correlation coefficients, are widely used to describe the correlation between random variables. However, correlation coefficients cannot describe the DS of correlated non-normally distributed random variables. Hence, copula theory is used to establish the joint probability distribution of random variables. There are different types of copula families, such as elliptical copula and Archimedean copula[14]. The Gaussian copula, one of elliptical copula functions, is stated as

(1)

wherex1,x2, …,xnare the random variables;F(xi) is the marginal cumulative distribution function(CDF) ofxi;φ=(Φ-1[F(x1)],Φ-1[F(x2)],…,Φ-1[F(xn)])Tis the vector of standard Normal variables andΦis the CDF of standard Normal variables;ρis the linear correlation coefficient matrix ofφ;Iis a unit vector.

The Gaussian copula is popular because of its ease in high-dimensional uncertainty modeling, but it fails to consider tail dependence between variables. On the contrary, other copula functions, such as Archimedean copula, describe the complex DS but they are only used for bivariate cases. The vine copula provides an effective method to model high-dimensional complex DS using pair-copula functions, which overcomes the deficiencies of Gaussian and Archimedean copula.

1.2 Vine copula

Canonical vine(C-vine) and D-vine are two typical vine copula constructions[12], which are shown in Figs. 1(a) and(b) for four-dimensional input variables, respectively. Each vine copula includes three treesTj(j=1, 2, 3) and each treeTjhas 4-jedges which correspond to 4-jpair-copula density functions. Forn-dimensional input variablesX, there aren(n-1)/2 pair-copula functions in vine copula. Using those pair-copula functions, the joint probability density function(PDF) ofXis derived[12].

Based on the C-vine copula, the joint PDF ofx1,x2, …,xnis established as

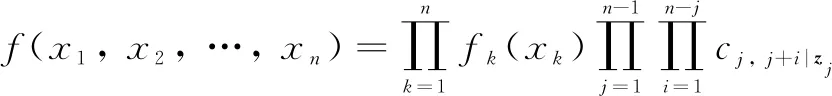
(2)

wherefi(xi) is the PDF ofxi;xzj=(x1,x2, …,xj-1)Tis a vector of random variables;zj=(1, 2, …,j-1);cj, j+i|zj| is a bivariate pair-copula density function;F(xj|xzj)| is a conditional CDF ofxjgivenxzj, which is stated as

F(xj|xzj)=|

(3)

wherexmis an arbitrary variable inxzj;xz (～m)represents other variables inxzjexcludingxm;Cj, m∣z (～m)is a bivariate pair-copula CDF.

Based on the D-vine copula, the joint PDF ofx1,x2, …,xnis established as

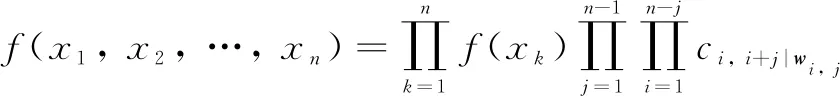
(4)

wherexw i, j=(xi+1,xi+2, …,xi+j-1)Tis a vector of random variables;wj=(i+1,i+2,…,i+j-1);ci, i+j|w i, j| is a bivariate pair-copula density function;F(xi|xw i, j|) is a conditional CDF ofxigivenxw i, j, which is stated as

F(xi|xwi, j)=|

(5)

wherexhis an arbitrary variable selected fromxwi, j;xw (～h)represents other variables inxw i, jexcludingxh;Ci, h∣w (～h)is a bivariate pair-copula CDF.

n(n-1)/2 pair-copula functions are used to establish the joint probability distribution ofnrandom variables. For each pair-copula function, the type of copula function is selected based on the Akaike’s information criterion(AIC)[15], and the parameters are estimated using the maximum likelihood estimation method.

2 Efficient PLF with Vine Copula

2.1 Sparse polynomial chaos expansion

SPCE obtains accurate PLF results with low computational burdens[16-20]. For stochastic problems withnindependent input random variablesξ=(ξ1,ξ2,…,ξn)T, the output random variableyis estimated by SPCE as

y=g(ξ)≈∑aiΨi(ξ),

(6)

whereaiis the coefficient of orthogonal polynomial baseΨi(ξ).

SPCE consists of three steps:(1) selecting samples of input variables;(2) obtaining samples of output variables by solving deterministic problems;(3) estimating coefficients of orthogonal polynomial bases. The superiority of SPCE over conventional PCE is that only significant polynomial bases are retained; thus, the number of bases is small in high-dimensional problems.

Input random variables should be independent when SPCE is used to evaluate output random variables. In order to apply SPCE to problems with correlated input random variables, Nataf transformation(NT) is commonly used to transform correlated variables into independent ones. However, NT only deals with correlation coefficients or Gaussian copula, and it is infeasible for vine copula-based DS[21].

2.2 RT for correlated variables

RT transforms correlated variables with vine copula-based DS into independent ones[14, 22-23]as follows.

Firstly, the joint PDF ofX=(x1,x2,…,xn)Tis presented using a series of conditional PDFs as

f(X)=f1(x1)f2(x2|x1|)f3(x3|x1,x2)|…fn(xn|xzn).|

(7)

Secondly, correlated variablesX=(x1,x2, …,xn)Tare transformed into independently and uniformly distributed random variablesU=(u1,u2,…,un)T. Moreover,Ucan also be transformed intoXby inverse RT. The relation betweenXandUis stated as

(8)

For the C-vine copula, the conditional CDFs in Formula (8) are obtained by Eq.(3), and thekth(k=2, 3, …,n) conditional CDF is

Fk(xk|xzk)|=

(9)

For D-vine copula, the conditional CDFs in Formula (8) are obtained by Eq. (5), and thekth(k=2, 3, …,n) conditional CDF is

Fk(xk|xzk)|=

(10)

Thirdly,ui(i=1, 2,…,n) is transformed into independent Normal variablesξi(i=1, 2, …,n) using the inverse CDF transformation as

ξi=Φ-1(ui).

(11)

Finally, for the independent random variablesξ1,ξ2, …,ξn, SPCE is used to solve the PLF problem. It is worth noting that for Gaussian copula-based DS, the results obtained by RT are the same as those by NT[24].

2.3 Proposed PLF method

Figure 2 depicts the procedure of the proposed PLF method, where RT is combined with SPCE to solve PLF with vine copula-based correlated input random variables. Meanwhile, the load flow model considers the impacts of input random variables as established in Ref. [9] and the PLF calculation is performed by Newton-Raphson method.

3 Case Study

The proposed PLF method is tested using the IEEE 123-bus system with 12 photovoltaic(PV) units. The topology structure of 123-bus system is shown in Fig. 3. The probability models of PV power are established using the data from NREL Solar Integration Data Sets[25], and three DS models are considered.(1) DS-INDE: correlations of different PV units’ power are neglected.(2) DS-GAU: PV power is modeled using Gaussian copula.(3) DS-MIX: PV power is modeled using C-vine copula with mixed copula families. The programs are performed with Matlab 2018 on a PC with Intel Xeon E5-2650 v4 2.20 GHz CPU and 64 GB of RAM.

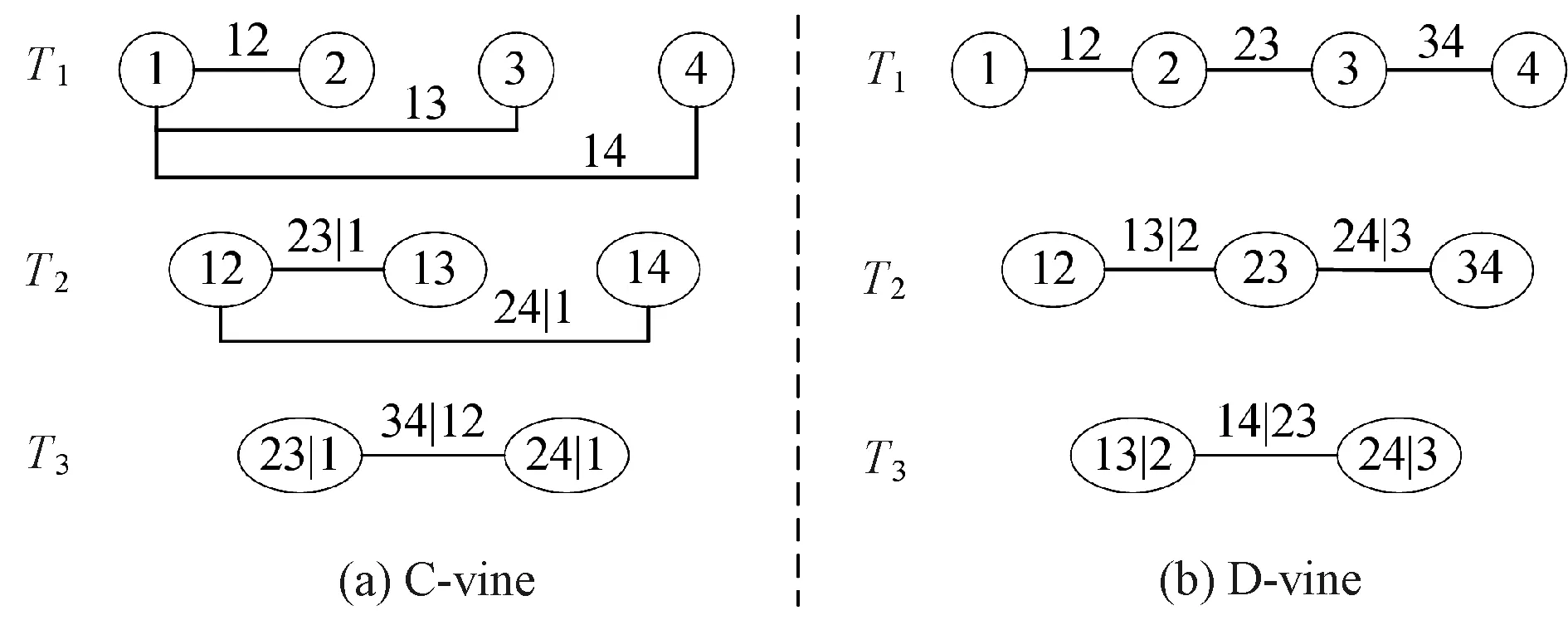
Fig. 1 Constructions of C-vine and D-vine copulas

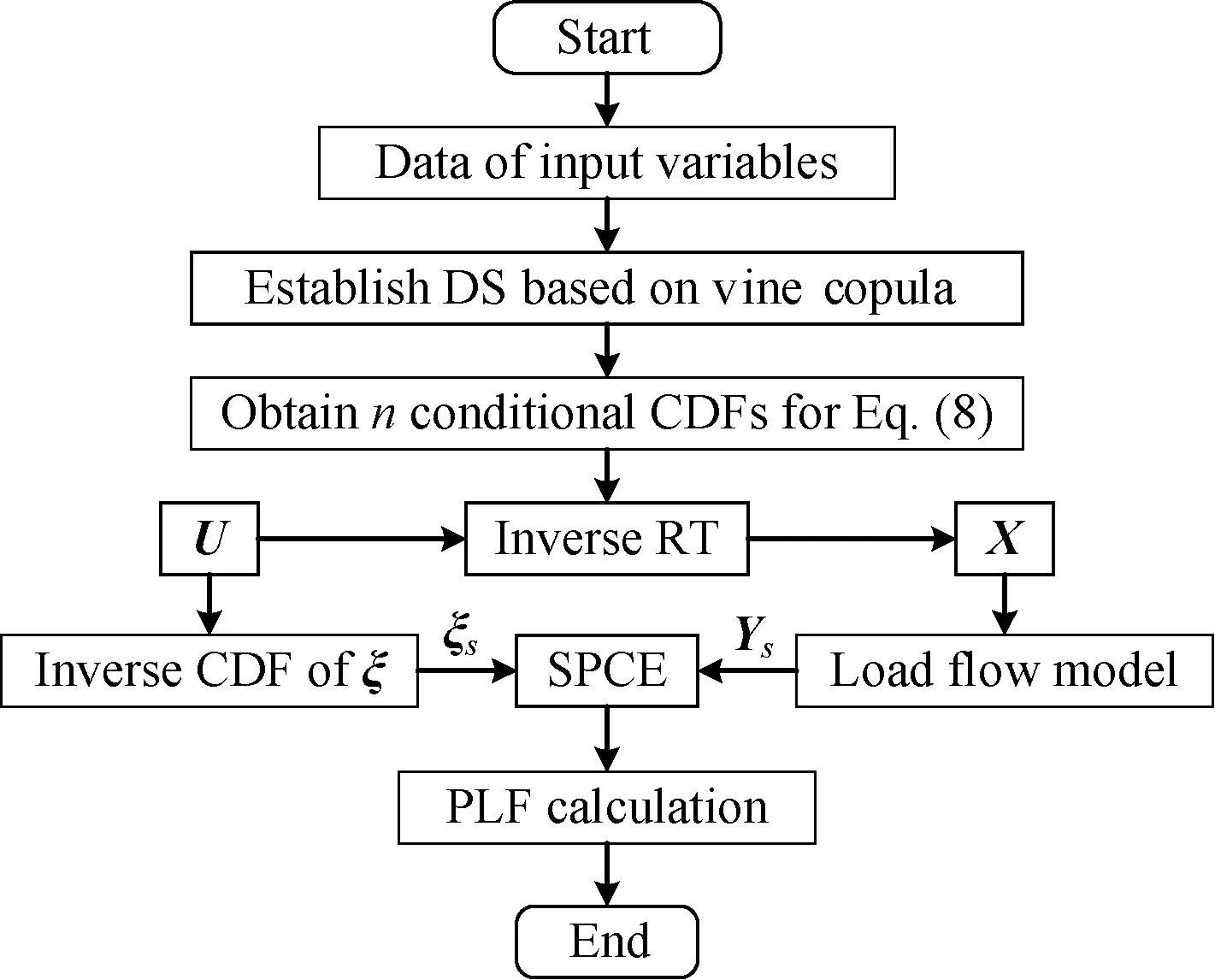
Fig. 2 Procedure of the proposed PLF method

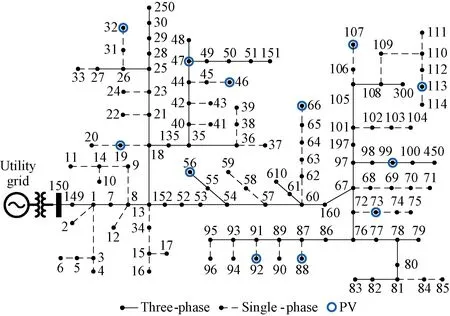
Fig. 3 Topology structure of 123-bus system

In this paper, results obtained by MCS with 10 000 samples are used as the benchmark to evaluate the performance of the proposed method. The correlations of PV power are described by the DS-MIX model, and the voltage magnitude of phase A of bus 34(V34) is given in Fig. 4. The CDFs of voltage magnitude obtained by the two methods are almost the same, which demonstrates the accuracy of the results of the proposed method. Moreover, as shown in Table 1, the total computation time of the proposed method is 767.66 s, which is much shorter than the time of MCS. Compared with MCS, the proposed method is much more efficient to obtain accurate PLF results. Furthermore, the CDFs of the voltage magnitude of phase A of bus 152(V152) and bus 45(V45) are shown in Fig. 5. The results of MCS and the proposed method are almost the same, which verifies the effectiveness of the proposed method.

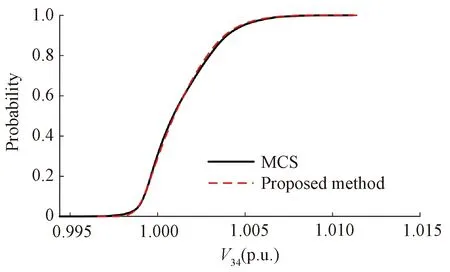
Fig. 4 CDFs of V34

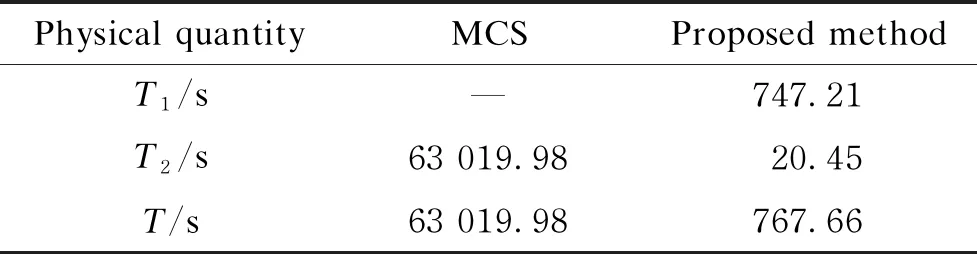
Table 1 Computation time of MCS and proposed method

In this part, the influence of DS on PLF results is analyzed. For different DS models, the PDFs and CDFs of voltage magnitude of phase A of bus 90 are compared in Fig. 6. In Fig. 6(a), the means ofV90corresponding to different DS models are almost the same. The DS of input variables mainly affects the variances of voltage magnitude rather than the means of voltage magnitude. Also, Fig. 6(b) indicates that the DS of input variables makes significant impacts on the tail probability(for example,V90<1.04 p.u.) of output variables. The results derived by PLF with Gaussian copula underestimate the probability of low voltage in the tail of distribution.

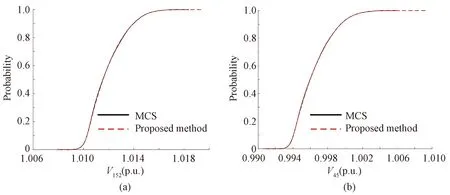
Fig. 5 CDFs: (a) V152; (b) V45

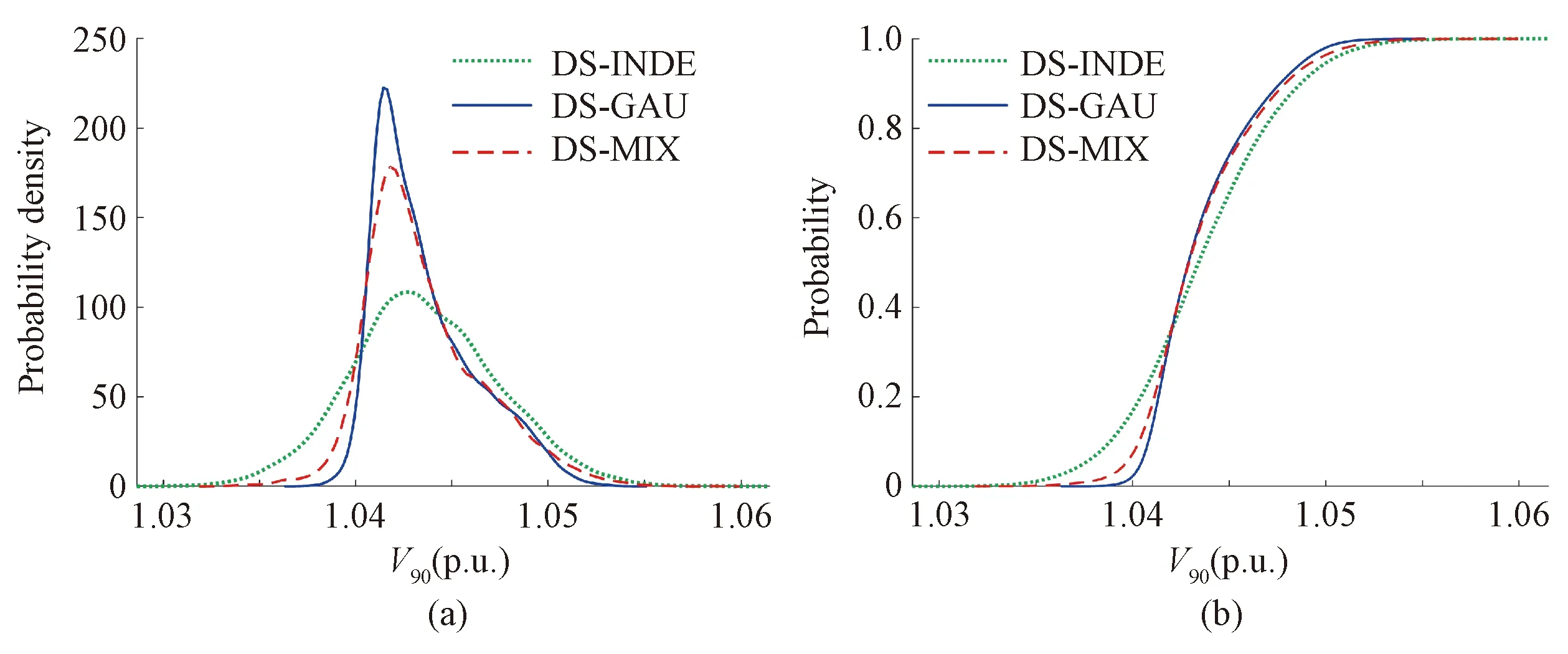
Fig. 6 PDFs and CDFs of voltage magnitude under different DS models: (a) PDFs of V90; (b) CDFs of V90

4 Conclusions

RT combined with SPCE is proposed to solve the PLF with vine copula-based correlated variables. Compared with MCS, the proposed method improves the computational efficiency of PLF calculation and maintains the accuracy of results. The proposed method efficiently handles the DS of input random variables, which makes a significant impact on probability distributions of power flow.