基于3阶模糊张量的广义加权几何算子及其应用

方世林，邓胜岳，吴海燕

（1.湖南理工学院 信息科学与工程学院，湖南 岳阳 414006；2.湖南工业大学 理学院，湖南 株洲 412007；3.株洲市第二中学，湖南 株洲 412007）

0 引言

多属性群决策作为现代决策科学的重要分支，一直是决策理论的研究热点[1]。信息集成技术是目前处理多属性决策问题的主要技术手段之一，也是决策理论与实践中的关键问题。因此，国内外许多专家学者针对决策信息集成的问题进行了较深入的研究，获得了一系列的研究成果。T.L.Saaty[2]于1980年首次提出并研究了加权几何算子。Xu Z.S.等[1,3-5]先后定义并研究了直觉模糊混合几何算子、最大和最小有序加权几何算子、直觉模糊有序加权几何算子等多属性决策方法。Chen S.M.等[6]构建了基于直觉模糊数和直觉模糊几何平均算子变换技术的多属性模糊决策方法。此外，针对实际决策环境的不同，专家们也提出了一些新颖的多属性决策方法和技术[7-9]。然而，以上研究工作的决策数据处理技术，均建立在矩阵分析理论的基础上。由于实际模糊多属性群决策中决策信息的模糊性和复杂性、决策数据规模的高维性，上述方法难以高效地处理此类问题。自 Qi L.Q.[10]与Lim L.H.[11]分别独立提出了张量特征值和张量特征向量的概念，进而吸引了许多专家从事张量理论及应用的研究。张量作为矩阵的推广具有高阶多维的特征，能将高维数据表示成非常简洁的形式；通俗来讲向量是一阶张量、矩阵是二阶张量，并且高阶张量能有效且简洁地解决具有高维数据特征的各类实际应用问题，如量子计算、图像降噪、晶体聚类等。

为了解决上述具有高维数据特征的多属性群决策问题，本文在已有研究成果的基础[12-14]上，定义了3阶模糊张量的一般形式，建立了基于3阶模糊张量的广义加权几何算子，探索了该算子的相关性质，进而提出了以广义加权几何算子为核心的决策方法，并通过数值算例验证了所提方法的有效性。

1 预备知识

本节将简要介绍3阶模糊张量的一般形式、运算法则以及相关性质，并规定文中将要涉及的符号。

F表示论域U上的模糊集合，Fn表示n维模糊向量，[n]={1, 2, …,n} ，TF(3,n1×n2×n3)表示3阶模糊张量集合。

2 基于三阶模糊张量的广义加权几何算子

本节将利用数学归纳法证明定义4中表达式的正确性，并给出定理1。此外，探索广义加权几何算子的基本性质，为后续算法设计提供理论基础。

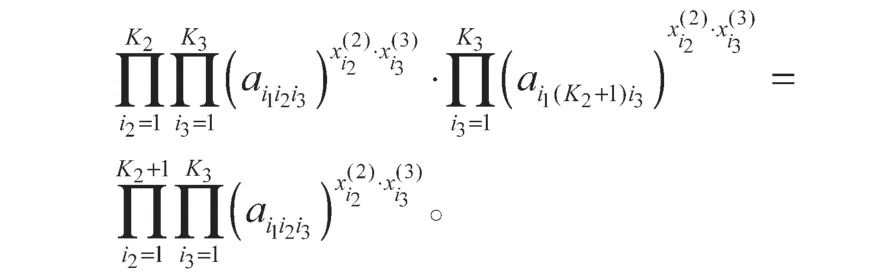
ⅱ）若n3=K3+1，则有

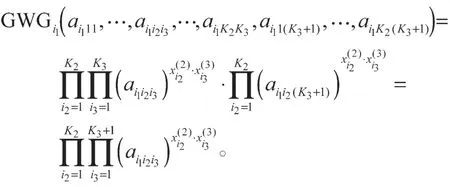
ⅲ）若n2=K2+1，n3=K3+1，则有

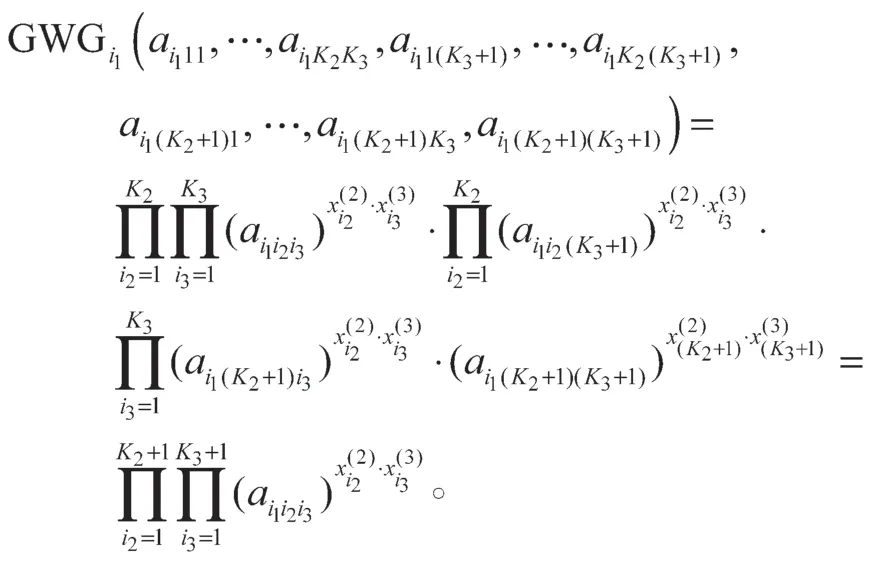
综上所述，对任意的n2,n3，等式（2）成立。

性质1定理1的集成值是n1维的模糊向量。

证明根据定理1，有

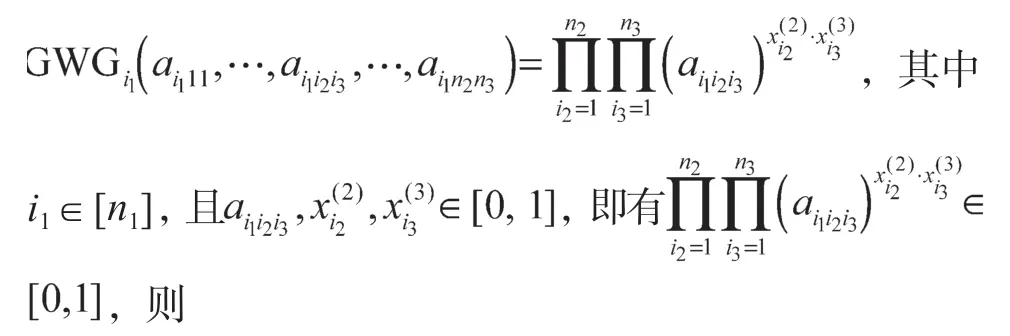
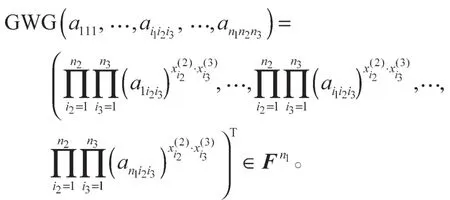
因此，定理1的计算值为n1维的模糊向量。

且i1∈[n1]，则有

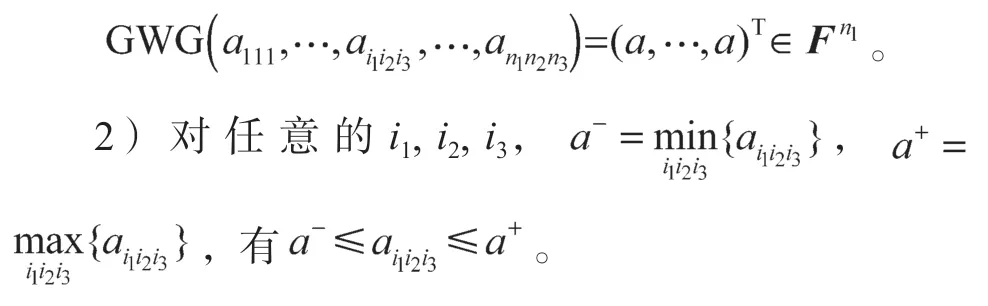
由定理1可知，广义加权几何算子第i1个分量有关系式

3 算法

本节将利用基于3阶模糊张量的广义加权几何算子设计算法，为解决多属性决策问题提供一种新的方法，该算法具体如下：

步骤1将决策数据的模糊矩阵表示法转换为3阶模糊张量的表示；

步骤2根据定理1的结论，利用广义加权几何算子（GWG），将模糊张量表示的决策数据（i1∈[n1]，i2∈[n2]，i3∈[n3]）进行数据集成，从而获得与备选方案对应的模糊数值；

步骤3根据步骤2的计算结果，进行模糊数排序，进而得到最优的排序方案。

4 数值算例

本节采用文献[15]中的例题作为算例来说明本文所提方法的可行性。

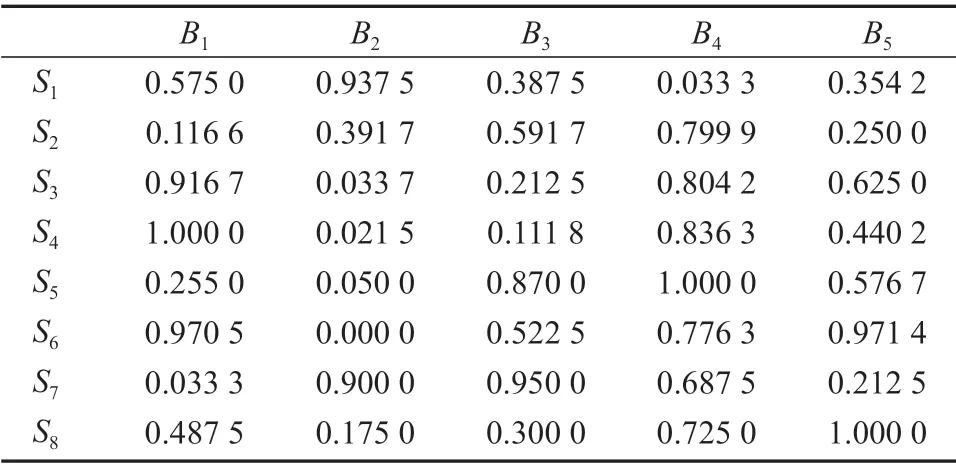
表1 决策者D1的标准决策矩阵R1Table 1 Standardized decision matrix R1 for decision maker D1

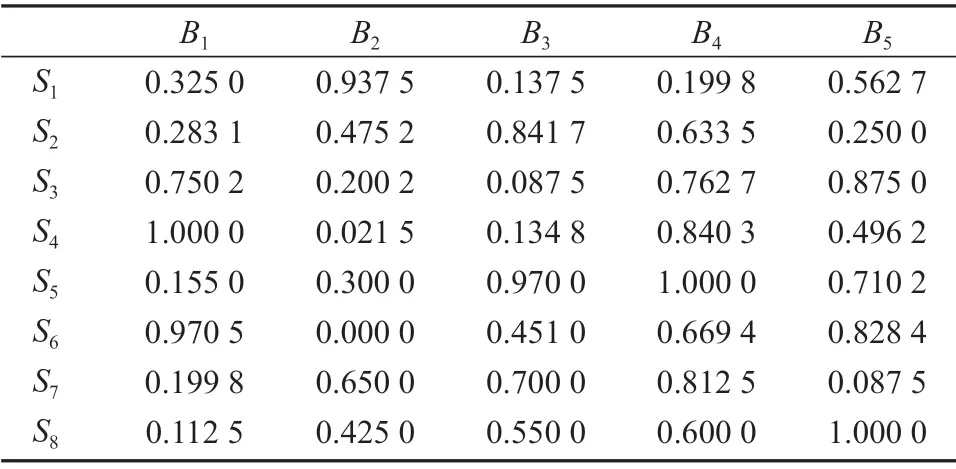
表2 决策者D2的标准决策矩阵R2Table 2 Standardized decision matrix R2 for decision maker D2

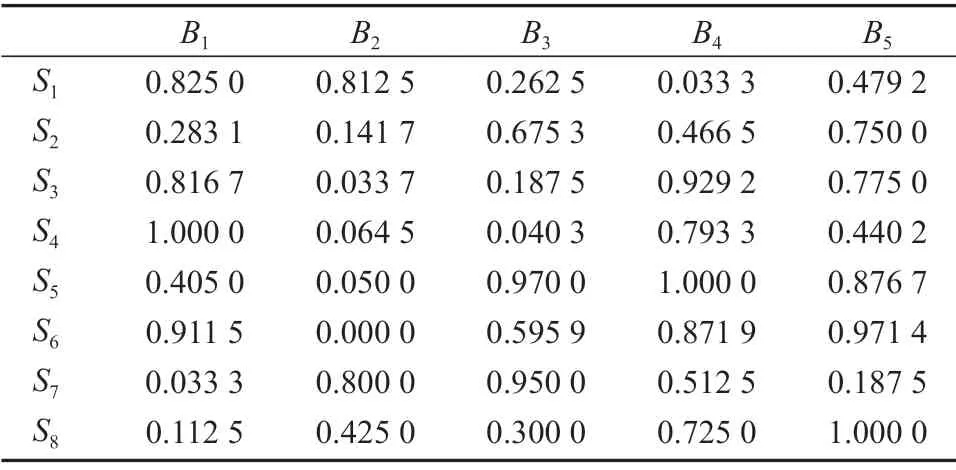
表3 决策者D3的标准决策矩阵R3Table 3 Standardized decision matrix R3 for decision maker D3

利用本文的算法求解该问题，具体步骤如下。

步骤1利用3阶模糊张量表示表1～3的数据，即其中(i1=1, 2, 3,4, 5)表示5个备选方案，(i2=1, 2, 3)表示3个决策者，(i3=1, 2, …, 8)表示8个属性。

数据转换如下：

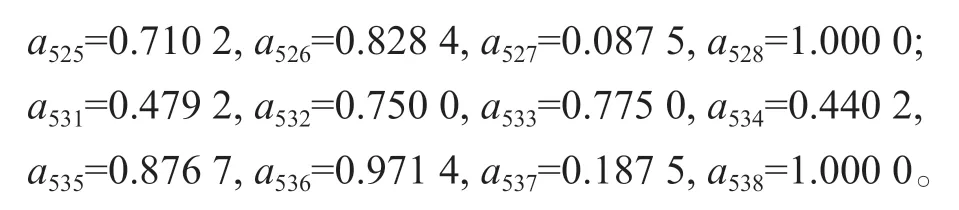
因此，本算例的最佳备选方案是b4。

5 结语

3阶模糊张量作为高阶模糊张量的基础表示形式，是研究高阶模糊张量性质和特征的基础。本文着重研究了3阶模糊张量的一般形式，建立了基于3阶模糊张量的广义加权几何算子，探索了广义加权几何算子的相关性质，提出了基于3阶模糊张量的多属性决策方法，并通过数值算例验证了本文所提方法的可行性。

数值算例的研究结果表明：

1）本文所提方法的计算结果同文献[15]的最佳备选方案结果一致，说明本文所提方法能够解决多属性群决策问题。

2）与文献[15]相比，本文所提方法的模型建立和计算过程更为简洁。

3）文献[12]和[14]没有涉及基于模糊张量的广义加权几何算子的研究，而本文所提方法恰好是文献[12]和[14]的补充。