钢筋-超高性能混凝土黏结性能的非线性有限元分析

张 哲，李帅帅，马永春，袁彬铖，蒋高旭

（湖南工业大学 土木工程学院，湖南 株洲 412007）

1 研究综述

钢筋-混凝土的黏结作用机理是影响结构服役期长短的重要因素之一，若黏结性能不足，则不仅无法充分发挥材料自身的性能，而且会引起界面间局部滑移过大，造成混凝土受钢筋约束作用弱化而产生构件表面裂纹，以至于未至服役期满即黏结失效。目前，国内外学者们关于钢筋与普通混凝土、高性能混凝土以及纤维增强混凝土的黏结性能进行了大量的研究[1-3]，研究成果较为丰富。超高性能混凝土（ultrahigh performance concrete，UHPC）[4]因具有优异的力学特性和耐久性，日渐成为土木工程结构理想的建筑材料。黏结性能对钢筋混凝土结构的破坏模式影响较大，因普通混凝土抗拉强度较低，与钢筋共同受力时易发生黏结失效而破坏；而UHPC材料具有优异的拉伸应变硬化性能，且其极限拉应变与钢筋屈服应变相近，若黏结性能良好便可以与钢筋共同变形与受力。由此可见，黏结性能是配筋UHPC构件优异结构性能的基础，故研究钢筋与UHPC界面间的黏结性能，对配筋UHPC的结构设计、施工等具有重要的现实意义。

近年来，国内外的专家学者们已经对钢筋与UHPC之间的黏结作用机理进行了相关的试验研究。如文献[5-11]分别研究了光圆钢筋、变形钢筋和纤维增强塑料筋等与UHPC的黏结性能，研究结果表明，配筋UHPC的界面黏结强度约为普通混凝土的5～10倍。Yoo D.Y.等[8]的研究结果表明，由于黏结界面应力分布的非线性和泊松比效应，钢筋与UHPC间的黏结力与黏结长度和钢筋直径增幅相反。Yuan J.等[10]基于拉拔试验研究了黏结长度、UHPC保护层厚度、配筋间距和强度等级等因素对UHPC黏结性能的影响。E.Fehling等[12]采用12 mm的钢筋进行了拉拔试验，探讨了保护层厚度和黏结长度对配筋UHPC黏结性能的影响。Kim J.S.等[13]研究了UHPC的抗压强度、黏结长度和UHPC保护层厚度等对配筋UHPC黏结性能的影响。A.B.Sturm等[14]基于69个拉拔试验，研究了不同纤维种类对钢筋与UHPC黏结性能的影响。Hu A.X.等[15]探究了钢筋直径、钢纤维掺量和黏结长度等变量对高强钢筋与UHPC黏结性能的影响。P.Marchand等[16]研究了配筋直径、黏结长度以及保护层厚度对钢筋与UHPC黏结性能的影响。轩帅飞等[17]基于12组中心拉拔试验，研究了UHPC保护层厚度和锚固长度对钢绞线与UHPC黏结性能的影响，并且建议直径15.2 mm钢绞线的合理锚固长度为35倍钢绞线直径。安明喆等[1]以黏结长度和钢筋直径为变量对普通热轧变形钢筋与活性粉末混凝土（reactive powder concrete，RPC）间的黏结性能进行了研究，并且提出了直径为14～18 mm普通钢筋合理的锚固长度范围为3～4倍钢筋直径。贾方方[2]采用不同的试验方法，探究了配筋RPC的黏结性能，并且提出基于不同位置特征的黏结-滑移本构关系。邓宗才等[3]研究了高强钢筋RPC界面的黏结性能，提出了临界锚固长度和极限黏结应力的计算公式。孙明德等[18]通过中心和偏心拉拔试验方法探讨了黏结长度、保护层厚度、箍筋数量等变量对高强钢筋与RPC间黏结性能的影响。

有限元法和界面元法是钢筋混凝土界面黏结常用的数值分析方法[19]。肖小琼[20]和刘松[21]应用非线性弹簧单元模拟了锈蚀钢筋与普通混凝土的黏结性能，数值模拟结果与试验结果吻合较好；陈强[22]采用内聚力单元模型和双弹簧单元，分别对拉拔试验和梁式试验中钢筋与普通混凝土界面黏结性能进行了数值模拟，其结果与试验结果吻合良好；位世阳[23]采用内聚力单元模型对动态荷载作用下钢筋与普通混凝土间的黏结作用进行了有限元分析；高向玲等[24]应用界面元法对钢筋与普通混凝土界面的黏结性能进行了仿真分析；杜培荣[25]应用界面应力元法对钢筋与普通混凝土界面作用机理进行了模拟，分析了界面和缝间的荷载传递机理。试验研究是分析钢筋混凝土界面黏结性能常用的方法之一，但其结果离散型较大，得到的本构模型不具普遍适用性；相比于试验研究，数值分析是在有限元模型中引入黏结-滑移关系，并通过改变模型尺寸和加载条件以模拟各种作用下的黏结性能，具有试验周期短、可重复性强等优点。目前有关钢筋-UHPC黏结性能非线性仿真模拟的研究较少，因此本文拟基于文献试验的结果，利用非线性弹簧单元，以UHPC保护层厚度、配筋直径和黏结长度为变量，对配筋UHPC的界面黏结性能进行仿真分析，旨在为配筋UHPC黏结性能的影响参数研究提供参考。

2 模型尺寸及参数

UHPC保护层厚度（C）、配筋直径（d）和黏结长度（L）对配筋UHPC界面黏结强度及破坏形式等影响较大[1-3,13-18]，因此课题组将选取以上因素为变量，研究其对配筋UHPC黏结性能的影响，采用150 mm×150 mm×150 mm的UHPC立方体模型，同时选用HRB400钢筋，其长度为550 mm，钢筋-UHPC黏结模型的尺寸如图1所示（图中单位为mm）。有限元模型参数的选择参考文献[2, 3, 12, 15-16]的试验结果，具体参数见表1。

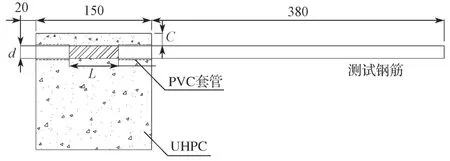
图1 钢筋-UHPC黏结模型尺寸Fig.1 Bond model of the reinforced UHPC

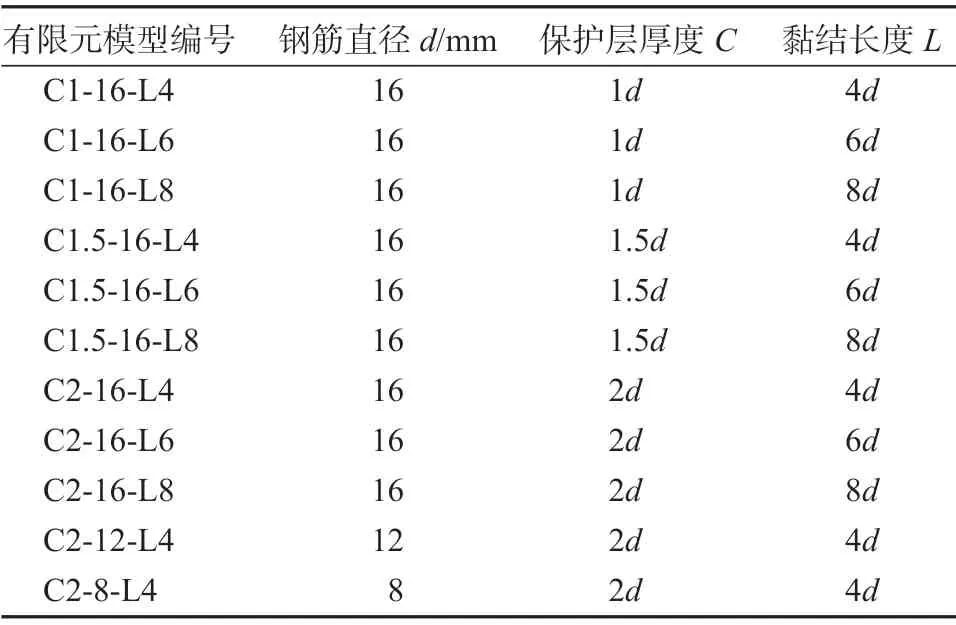
表1 有限元模型设计参数Table 1 Design parameters of the finite element model

3 钢筋-UHPC黏结-滑移本构关系

钢筋-UHPC间的黏结-滑移本构关系是影响有限元分析结果准确性的主要因素之一，因此合理选择黏结-滑移本构关系较为重要。由于配筋UHPC界面黏结作用机理复杂且影响因素较多，研究结果存在较大的离散性，因此不同学者的研究结果也存在着差异，表2列出了相关学者提出的黏结-滑移本构关系。

表2 配筋UHPC构件黏结-滑移本构关系Table 2 Bond-slip curves of reinforced UHPC members

4 黏结滑移有限元模型

4.1 有限元模型的建立

课题组采用ABAQUS建立配筋UHPC界面黏结模型，网格尺寸为5 mm，模型尺寸及边界条件如图2所示。

图2 黏结-滑移有限元模型Fig.2 Bond-slip finite element model

为有效模拟非线性特征，UHPC材料选用C3D8R单元模拟；配筋使用Beam单元（B31）模拟。黏结-滑移模拟过程中，采用以上单元模拟结果易收敛，且配筋的滑移误差较小。本文的配筋UHPC黏结-滑移模型采用易收敛的位移加载方式；同时在靠近荷载端UHPC界面施加固定约束。界面上钢筋与UHPC单元重合节点处采用弹簧单元以模拟其黏结区域的相互作用，通过修改Inp文件将弹簧单元设置为非线性弹簧单元Spring2，其刚度特性可基于式（1）计算得到，非线性弹簧单元如图3所示。

图3 弹簧单元节点布置及示意图Fig.3 Layout and schematic diagram of spring elements

弹簧单元节点力F为

式中：τ为黏结应力；dx为节点区域黏结长度。

4.2 材料参数

钢筋的受拉性能选用双折线本构模型，材料参数详见表3。

表3 钢筋材料参数Table 3 Reinforcement material parameters

基于受拉和受压两种混凝土失效模式，UHPC材料选取软件中的塑性损伤模型，能较好模拟UHPC的非线性行为，其详细参数见表4。

表4 UHPC材料参数Table 4 UHPC material parameters

UHPC受压应力(σ)-应变(ε)关系采用单波[26]提出的正则化无量纲关系式（6）。UHPC材料单轴受压的本构关系曲线[26]如图4所示。

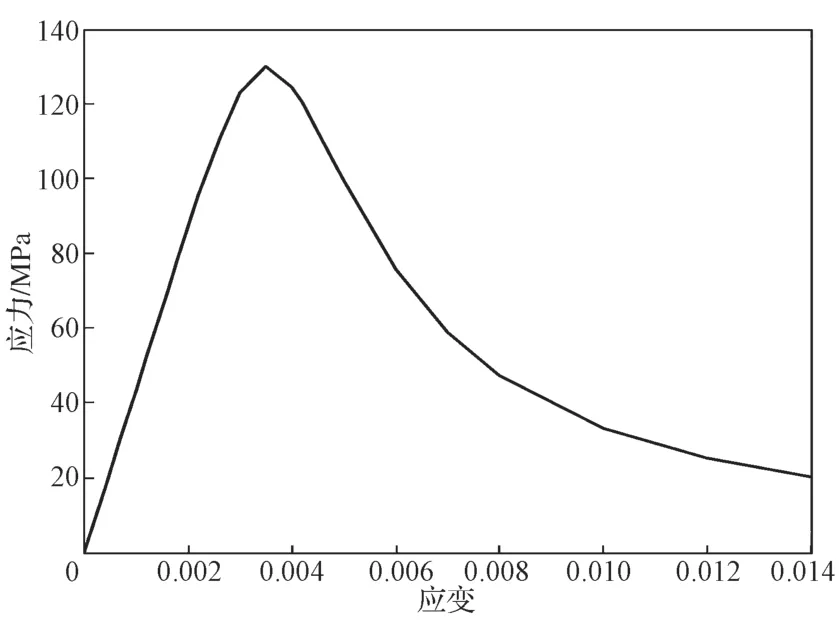
图4 UHPC材料的单轴受压本构关系曲线Fig.4 UHPC material compressive constitutive curve

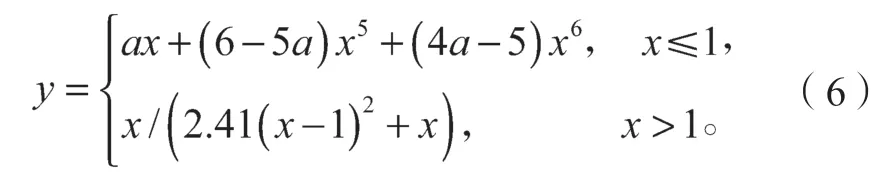
式中：y=σ/fc，其中fc为抗压强度；x=ε/ε0，其中ε0是峰值应变；a为初始切线模量与割线模量比。

本模型中fc取135 MPa，ε0为3 500 µε，a为1.177。

图5和式（7）给出了本文采用的UHPC材料受拉应力(σ)-应变(ε)关系[27]。

图5 UHPC材料拉伸本构关系曲线Fig.5 UHPC material tensile constitutive curve

式中：fct为UHPC应变硬化平均应力；εca和εpc分别为初裂应变和极限应变。

本模型中fct取8.9 MPa，εca和εpc分别取192和1 784。

5 有限元结果分析

Mises应力[20]是基于结构剪切应变能的一种等效应力，可较好地表征配筋UHPC界面间的黏结应力，图6给出了有限元分析计算的Mises应力和位移图。图中单位：应力为Pa，位移为m。

图6 不同黏结长度模型的应力和位移云图Fig.6 Stress and displacement contours of FE models with different bond lengths

由图6可知：UHPC的应力沿黏结长度影响区域呈球形分布，距黏结影响区域越远，应力越小；而应力最大值主要分布在近载端附近，从近载端至远端应力值逐渐降低；UHPC保护层厚度不变时，Mises应力随黏结长度的增加而增长；配筋的位移沿近载端至黏结末端逐渐变小，黏结末端的位移随着黏结长度的增加而逐渐变小。

5.1 相对黏结长度对黏结性能的影响

图7给出了经过有限元仿真得到的钢筋-UHPC界面随相对黏结长度变化的黏结-滑移曲线。由有限元仿真结果图可以知道，不同黏结长度模型加载初期黏结-滑移曲线基本吻合，该结果表明初始黏结应力主要源于界面间的化学附着力；当黏结应力大于5～10 MPa时，钢筋-UHPC界面滑移逐渐增加，化学胶着力消失，不同组模型的黏结-滑移曲线发生相应变化，黏结应力随着滑移量的增加而呈现较快增长；当黏结应力值高于15～25 MPa后，UHPC发生破坏，黏结应力增加相对较少，而滑移量迅速增加。当其它因素不变时，不同组模型的极限黏结应力均随着相对黏结长度的增加而减小，如当保护层厚度等于钢筋直径时，随着相对黏结长度从4d增至6d和8d，极限黏结应力约分别降低了17.6%和23.9%；类似地，保护层厚度为1.5倍和2.0倍钢筋直径时，极限黏结应力降幅分别为17.8%～25.3%和14.7%～20.5%。

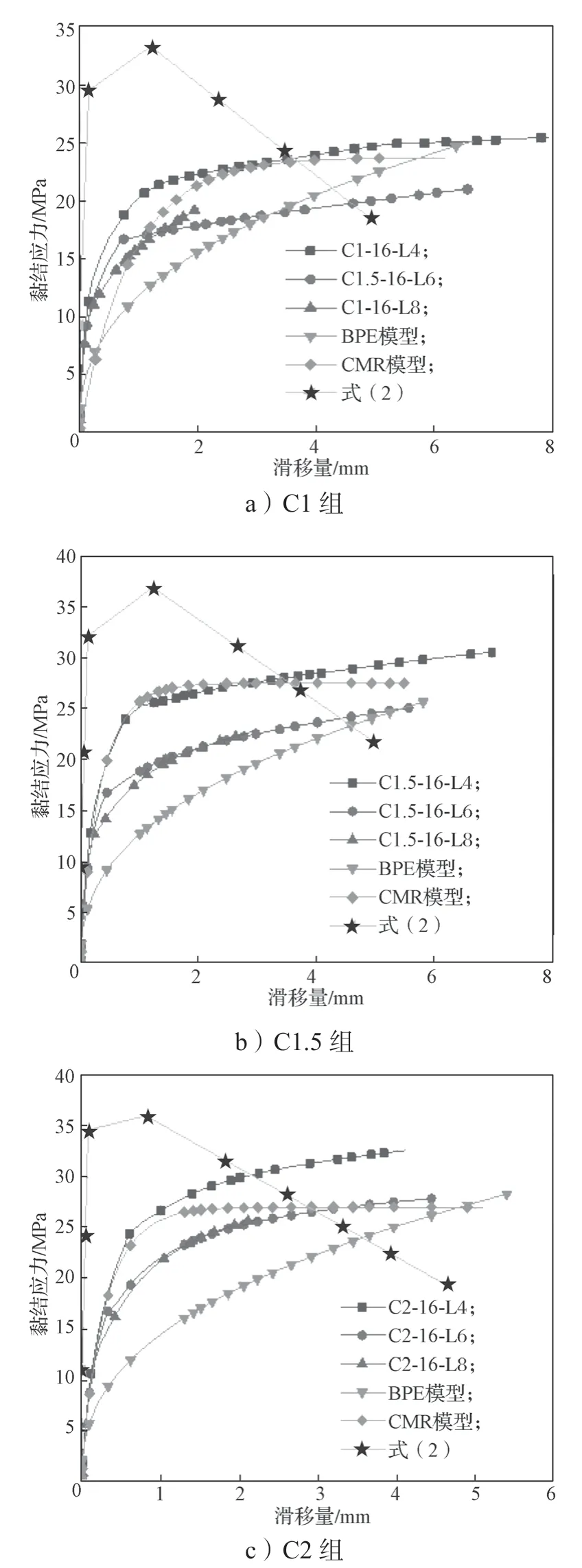
图7 不同黏结长度的黏结-滑移仿真曲线Fig.7 Bond-slip simulation curves with different bond lengths

文献[1-3, 15-16, 18]研究了钢筋与UHPC间的黏结性能，均发现极限黏结应力随着相对黏结长度的增加而降低。由于黏结应力沿钢筋长度不均匀分布和泊松比效应对黏结性能的影响，相对黏结长度越长，界面应力分布越不均匀，高应力部分相对短而窄，因此本文中不同组模型的峰值黏结应力随着相对黏结长度的增大而降低。

5.2 相对保护层厚度对黏结性能的影响

有限元模型通过改变钢筋表面距UHPC表面的距离，模拟不同保护层厚度对黏结性能的影响，分析结果如图8所示。

图8 不同保护层厚度的黏结-滑移仿真曲线Fig.8 Bond-slip simulation curves with different cover heights

由图8可知，不同保护层厚度模型初期的黏结-滑移曲线基本吻合，黏结应力大于5～10 MPa时，钢筋-UHPC界面滑移逐渐增加，黏结-滑移曲线不再吻合，黏结应力随滑移量的增加而逐渐增加。其它因素不变时，不同组模型的极限黏结应力随保护层厚度的增加而增加，而峰值滑移与其相反，黏结长度为4倍钢筋直径时，相对保护层厚度从1.0d增至1.5d和2.0d，极限黏结应力约分别增加了19.5%和27.6%；类似地，黏结长度为6倍和8倍钢筋直径时，极限黏结应力增幅分别为19.3%～32.2%和17.3%～33.3%。

文献[1-3, 12, 15-16, 18]研究了钢筋与UHPC间的黏结性能，均发现一定范围内极限黏结应力随着相对保护层厚度的增加而增加。钢筋与UHPC界面发生相对滑移会对周围UHPC产生挤压力使UHPC环向受拉，保护层厚度不足时，若环向拉应力大于UHPC的抗拉强度则使UHPC提前破坏，钢筋材料性能无法有效利用且极限黏结应力相对较小；保护层厚度较大时，UHPC对变形钢筋的环向作用增加使钢筋肋前混凝土被剪碎，钢筋最终发生拔出破坏或被拉断。

5.3 钢筋直径对黏结性能的影响

选用不同的钢筋直径对钢筋-UHPC界面黏结性能进行了有限元模拟，其分析结果如图9所示。

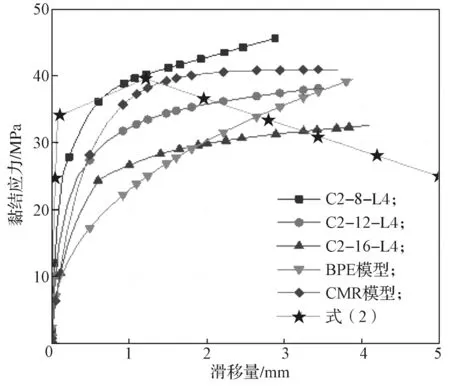
图9 不同钢筋直径的黏结-滑移仿真曲线Fig.9 Bond-slip simulation curves with different rebar diameters

由图9可知，不同配筋直径模型的黏结应力-滑移曲线前期发展基本一致；黏结应力大于5～10 MPa时，钢筋-UHPC界面产生滑移，黏结-滑移曲线发生变化，极限黏结应力随配筋直径的加大而降低，这类似于文献[3, 8, 18]的试验结果，但有别于部分文献[15-16]的研究结果。造成研究结果分歧的原因，可能在于配筋表面的泌水性随其直径增加而加大，引起钢筋-UHPC界面间隙增加，相对黏结面积变小使得黏结应力分布更不均匀，最终极限应力减小，但钢筋-UHPC界面黏结机理复杂且受多种因素的影响，因此不同学者的研究结果可能存在差异，有关配筋直径对配筋UHPC界面黏结性能的影响有待深入探讨。当黏结长度为4倍钢筋直径、UHPC保护层厚度采用2倍配筋直径时，随钢筋直径从8 mm增加为12 mm和16 mm，其极限黏结强度的降幅约分别为16.5%和28.8%。

5.4 模拟结果比较

对于不同钢筋黏结长度、UHPC保护层厚度和配筋直径的有限元模型，将其数值分析结果分别与式（2）和式（3）的BPE模型和CMR模型计算结果进行比较，见图7～9。由图可见，各组有限元模型结果和CMR模型计算结果较接近，BPE模型计算结果次之，而同式（2）的计算结果比较，仅图9中不同钢筋直径时与模拟结果较接近，其余误差均较大，由此可知，CMR模型更适用于预测钢筋-UHPC界面的黏结-滑移曲线。

表5为各组模型模拟结果和式（4）的计算结果对比，由表可知，各模型模拟结果的极限黏结强度与式（4）计算结果误差较小，其误差均值为2%，非线性弹簧单元用于模拟配筋UHPC界面的黏结-滑移本构关系是可行的，但该模拟亦存在一定的局限性，其不能直接模拟钢筋与UHPC间的咬合作用而推算两者间的黏结应力。

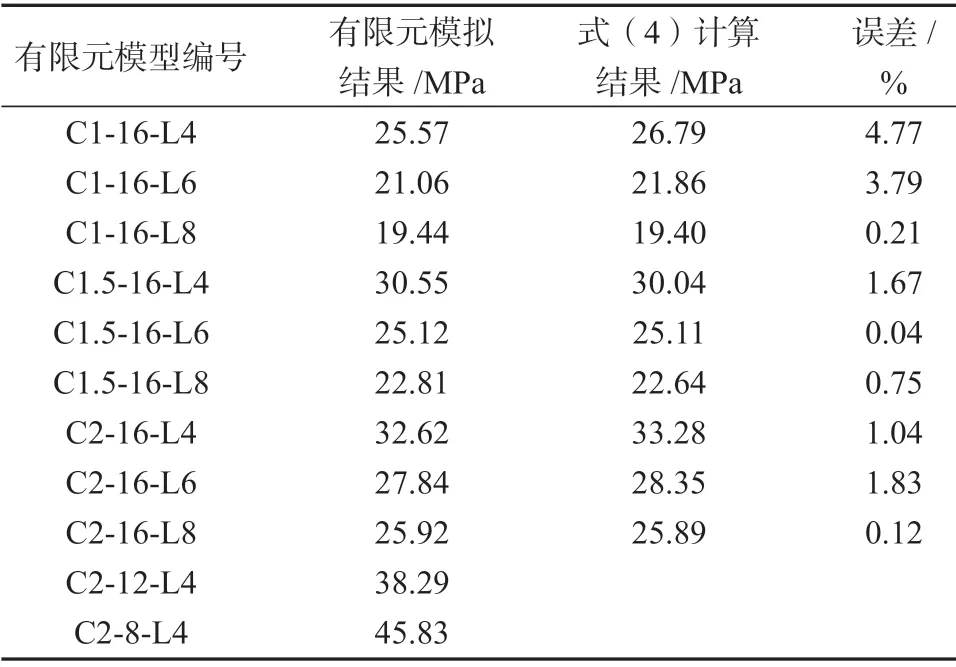
表5 有限元分析结果与现有文献计算结果对比Table 5 Comparative results of finite element analysis and existing calculation results

6 结论

通过ABAQUS有限元软件非线性弹簧单元分别模拟了不同UHPC保护层厚度、黏结长度和配筋直径下配筋UHPC界面黏结-滑移曲线，并探讨各参数对界面黏结的影响，得出的结论如下：

1）极限黏结应力随保护层厚度增加而提高，而峰值滑移的变化趋势则相反，黏结长度为4倍钢筋直径时，保护层厚度从单倍钢筋直径增至1.5倍和2.0倍钢筋直径时，极限黏结应力约分别增加了19.5%和27.6%；黏结长度为6倍和8倍钢筋直径时，极限黏结应力增幅分别为19.3%～32.2%和17.3%～33.3%。

2）随着配筋直径和黏结长度的增大，配筋UHPC的极限黏结应力逐渐降低；配筋直径从8 mm增至12 mm和16 mm，极限应力约分别降低16.5%和28.8%，黏结长度从4倍钢筋直径增加至6～8倍钢筋直径，极限黏结应力降幅为14.7%～25.3%。

3）对于极限黏结应力，有限元分析结果与文献计算结果误差均值为2%，表明非线性弹簧单元用于模拟配筋UHPC界面黏结的非线性具有可行性；黏结-滑移曲线与文献中的CMR模型吻合较好，可以为配筋UHPC黏结性能非线性有限元分析提供参考。