基于改进PCA-KELM的特征提取算法

赵柏山，朱孟珍

（沈阳工业大学 信息科学与工程学院，辽宁 沈阳 110870）

0 引言

随着机器人在各个领域的发展和广泛应用，人们对机器人的精度要求也进一步提高。机器人动力学系统由于受到很多的非线性的因素干扰，从而使得机器人的建模十分困难。与特征选择类方法不同，特征提取方法是将原始数据映射到低维的空间，从而达到降维的目的。常用的特征提取的方法有许多，本文主要使用的是应用广泛的主成分分析法（PCA）。极限学习机（ELM）是近年在神经网络的基础上发展起来的一种单隐层的前馈神经网络[1]。与传统的神经网络相比，极限学习机的各方面性能都得到了提升，比如提高了训练学习的速度，解决了传统的神经网络容易陷入局部极小的问题。

本文将结合PCA与ELM两种方法，针对机械臂的状态信号进行特征提取，提出一种改进的PCA-KELM算法，结合多分类方法分析机械臂系统中的非线性因素与特征值之间的关系，以便于以后的建模和后续研究。

1 主成分分析（PCA）

通过PCA[2]方法能将原本巨大的数据量压缩到较小的数据量，而且其基本信息不会丢失。PCA的核心思想就是降维，PCA算法的具体步骤如下。（1）整理原始的数据矩阵：Xm×n；（2）求原始矩阵Xm×n的协方差矩阵Cov(X)；（3）求协方差矩阵的特征值和其对应的特征向量；（4）选取最大的K个特征值及其对应的特征向量，使其构成矩阵Wn×k；（5）计算得到矩阵Zm×k=Xm×nWn×k。

2 核极限学习机(KELM)

ELM算法随机产生输入层与隐含层间的连接权值以及隐含层神经元阈值，且在训练过程中无须多次调整，只需要配置隐含层神经元的数目，选择合适的激活函数，就可以获得唯一的最优解[3]。极限学习机的网络结构是单隐含层的，其中n是输入层的神经元数目，l是隐含层的神经元数目，m为输出层的神经元数目。

w为输入层与隐含层之间的连接权值，可表示为：

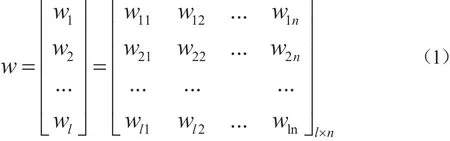
β是隐含层与输出层间的连接权值，可表示为：

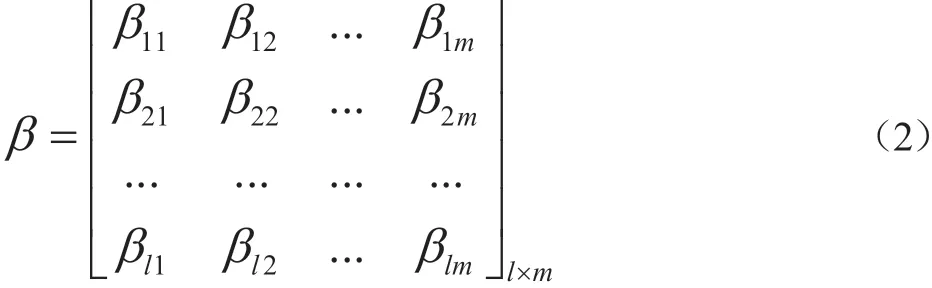
隐含层阈值为：

设激活函数为g(x)，则网络的输出为：

式（4）可以表示为：

其中，T'为矩阵T的转置。

其中，H+为隐含层输出矩阵H的Moore-Penrose广义逆。关于H+的计算有多种方法，使用正交法[4]计算，当HHT矩阵为非奇异时，则H+=HT(HHT)-1。

将正则化系数1/C加在HH+的对角线上得到：

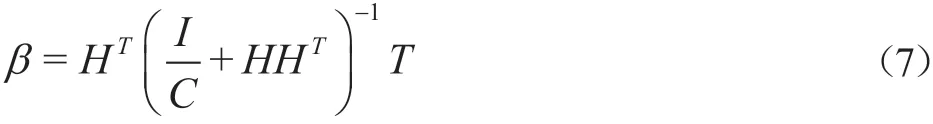
核极限学习机[5]就是在极限学习机的基础上，引入核函数这个概念，利用Mercer条件构造核矩阵来代替其HH+。

于是式（7）可以表示为：

则极限学习机的输出函数为：

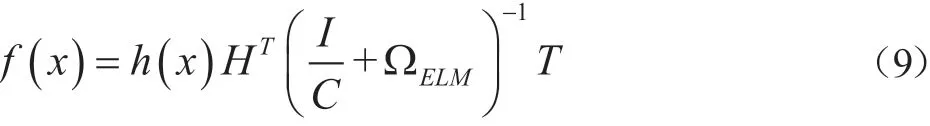
3 多分类算法

多分类问题最初是用于支持向量机，主要的方法有一对一（OAO）算法，决策二叉树（BT）算法以及方向无环图（DAG）算法等。

3.1 一对一（OAO）法

对于K(K>2)类的分类问题，将全部的类别中的任意两类组成一个二分类器，共计构成[K(K－1)]/2个二分类器[6]。在测试的时候，将样本经过全部的[K(K－1)]/2二分类器，每个分类器都作出一次判断，将这一样本归为某一类。最后得票最多的就是该样本所属的类别。

3.2 决策二叉树（BT）法

BT法在进行多类判别时，首先把全部的类别划分为两类，然后再将这两个类别内部划分为两个子类别，直到所有的小类中都只含有一类为止[7]。这样只需要构造K－1个二分类器。

3.3 有向无环图（DAG）分类方法

DAG分类算法可以理解为OAO算法和BT算法的结合，把有向无环图的思想引入到对OAO算法中，把多个分类器组合成一个多元分类器[8]。对于一个K类问题，DAG算法中有[K(K－1)]/2个节点，有[K(K－1)]/2个二分类器。

4 改进的PCA-KELM算法应用于机械臂系统

4.1 柔性关节机械臂建模

本文主要针对柔性关节机械臂的关节刚度问题做了研究[9-10]。柔性关节机械臂动力学方程为：

其中，m1，m2分别表示连杆1、2的质量，L1，L2分别表示连杆1、2的长度，l1，l2代表两个杆的质心位置。g为重力加速度，qm1，qm2分别表示电机1、2的转角，ql1，ql2分别表示连杆1、2的转角，τ1，τ2分别表示两个关节的控制力矩。Dm(qm)表示电机惯量，D1(q1)表示连杆的惯性矩阵表示科氏力和离心力，τ表示电机的输入力矩，Ng表示齿轮的减速比，Kg表示关节刚度。

4.2 算法实现

以下实验结果均是基于关节1处的仿真数据进行的特征提取实验。根据柔性关节的刚度不同，将数据分为5类。得到的数据集为1 600×10 001的原始特征矩阵。

针对ELM算法提出改进。ELM算法本身可以用于多分类的问题，但是其对于多分类问题的处理效果较差，于是我们考虑改进其多分类的算法。具体的改进方式是将支持向量机中多分类的方法引用到KELM中，使用OAO，BT和DAG 3种不同的算法处理分类问题时的多分类问题。得到仿真结果如图1所示。

图1中，粗体的圆圈代表样本点经过测试估计的类别，偏细的点代表该样本点正确的分类。3种方法的分类效果都不错，粗体的圆圈几乎把偏细的点全部覆盖，只有零散的几个点识别错误。

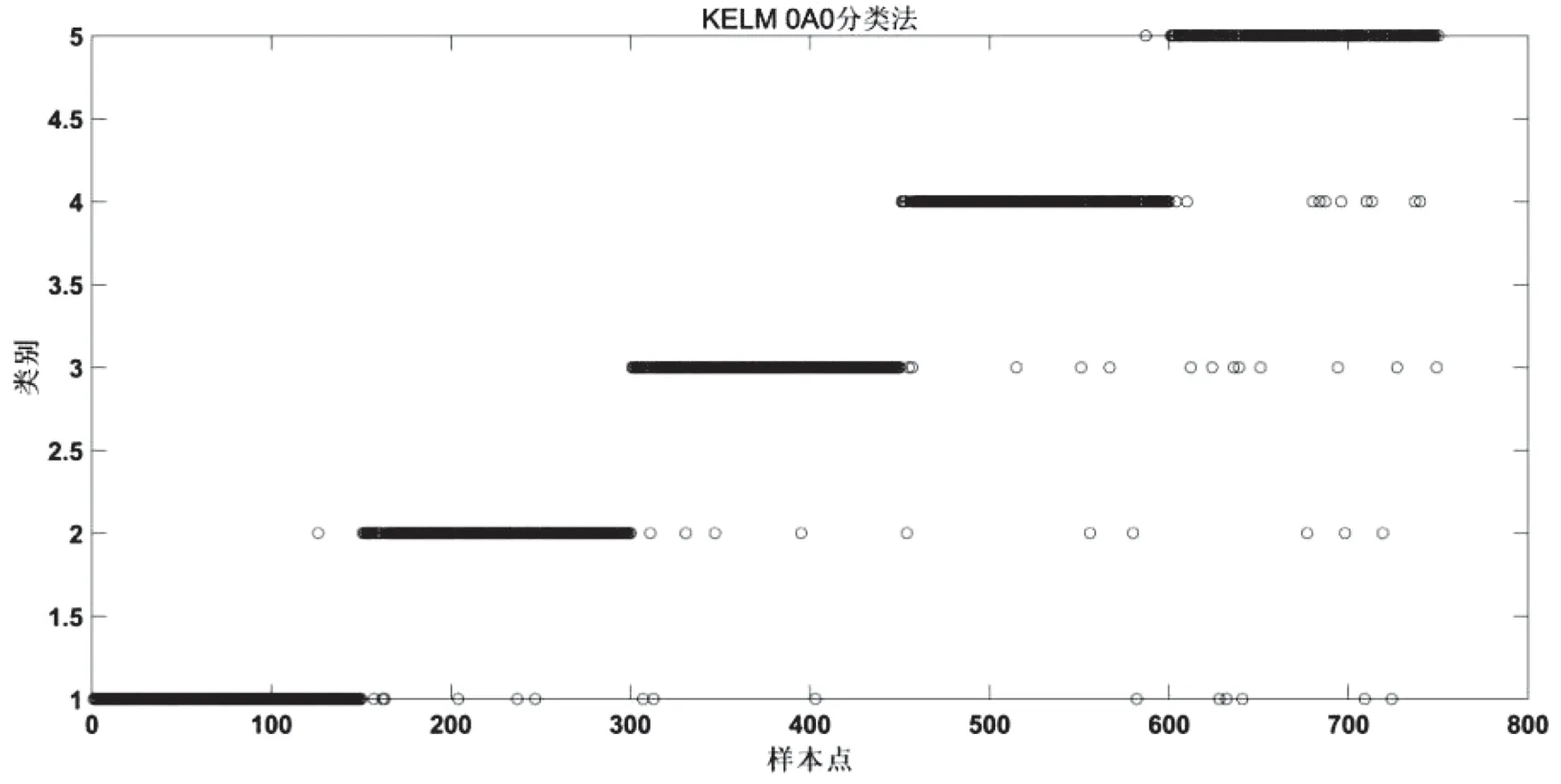
图1 PCA-KELM-DAG算法结果

之后我们再使用传统的PCA-ELM算法与其对比，对比结果如表1所示。

表1 不同算法的结果对比

从表1可以看出，改进的PCA-KELM算法对比传统的PCA-ELM在测试集的正确率上有了很大的提升。3种多分类算法的正确率都比较高，算法效果比较优秀，其中BT分类算法的测试集正确率比其他两种分类方法的测试集正确率稍高。

5 结论

基于PCA算法的KELM算法，首先将原本高维的数据通过PCA算法进行特征提取实现降维，再利用KELM 算法结合多分类方法识别样本的刚度属于哪一区间。仿真结果表明，该算法的正确率相比于传统的PCA-ELM算法有了大幅的提高。本文的研究为今后的柔性关节机械臂的建模建立了基础，方便了后续的关于柔性关节机械臂的相关研究。