融合遗传和粒子群算法的云工作流调度算法
2021-11-01张宇
张 宇
(河南财政金融学院 软件学院,河南 郑州 450000)
0 引 言
云计算工作流调度由于其NP难属性得到了广泛研究,工作流应用需要大容量存储空间基础设施和更高的快速并行执行度,而云计算由于可以通过虚拟机化方式以即付即用模式提供基础设施,使其成为适用于工作流调度的有效平台[1-3]。然而,为了提供服务,实现不同目标优化,如执行跨度、执行代价、负载均衡或者能效调度,需要设计有效的工作流调度策略。近年来,多种类型的工作流调度算法已被提出。需要注意的是,给定任务组成的工作流和虚拟机集合,工作流调度可行解是指数级的,生成工作流调度解需消耗大量计算时间和存储空间。而元启发式算法,如遗传算法、粒子群算法成为可以在合理时间和空间内找到近似最优解的可行算法。然而,研究[4]表明混合式元启发式算法比单一算法性能更好。
本文在云环境中提出一种混合元启发式工作流调度算法,同时实现执行跨度优化和负载均衡。算法融合遗传算法和粒子群算法进行工作流调度问题求解。虽然已有算法[5,6]也将遗传算法和粒子群算法混合对任务调度求解。然而,仅仅是独立任务调度问题,不适用于云工作流调度。设计算法利用两个核心操作,即遗传算法中的交叉和变异操作融入粒子群算法的迭代过程中。粒子群相比遗传算法收敛更快,而粒子群算法的限制在于其高维度搜索空间中易于陷入局部最优,且遗传算法同样也有慢速收敛问题,混合元启发式算法将同时避免两种算法的限制。为了评估算法性能,通过科学工作流进行仿真实验,并与单一元启发式算法进行对比,验证了算法性能更优。
1 相关工作
近年来,多种启发式和元启发式方法被提出解决工作流调度问题。文献[7,8]研究了应用模拟退火和禁忌搜索算法求解网格环境中的工作流调度问题。文献[9]中,作者将执行跨度和能量考虑为调度目标,利用一种两阶段遗传算法通过多父代的交叉操作得到了调度最优解。文献[10]中,作者设计了一种改进的遗传算法IGA对工作流调度时进行虚拟机选择,比原始遗传算法得到更好的调度解。文献[11]提出了一种混合启发式方法进行工作流调度,其调度方法首先赋予任务优先级,然后利用遗传算法改进任务与虚拟机资源间的映射解。文献[12]设计一种融入了引力搜索算法的混合启发式工作流调度算法,算法同时将异构最早时间算法HEFT得到的解融入到引力搜索算法的初始解中,同时引入时间与代价因子得到代价有效的调度解。Min-Min和Max-Min算法是网格系统中常用的任务调度算法。然而,这些算法频繁应用在云计算环境中,性能已经达到上限。Min-Min算法[13]作为一种启发式算法,以未映射的任务集作为开始,寻到能够得到最小期望执行时间的调度方案。这种算法的不足在于越大的任务比越小的任务会等待更长的时间,进而导致长任务的饥饿问题。
Max-Min启发式算法中[14],未映射任务集合中拥有最大完成时间的任务被分配至最小执行时间的资源上。该调度算法的不足在于,最大完成时间的任务将优先执行。因此,会增加工作流的执行跨度,并且使得较小完成时间的任务具有更长的响应时间。文献[15]提出一种基于遗传算法的任务调度负载均衡算法,其考虑的调度参数包括执行跨度和资源上的负载均衡。文献[16]提出了基于遗传算法的任务调度算法,算法设计了一种关键路径遗传算法,同时利用了两个适应度函数进行了染色体的编解码。文献[17]提出了可靠性驱动的方法,基于信誉值的考虑度量虚拟机资源的可靠性,并利用前向遗传算法进行工作流调度,实现调度资源的可靠性和执行跨度最小化。然而,文献中的方法并没有考虑通信开销,而该因素是工作流调度中必须考虑的因素。文献[6]将变异引入到粒子群算法中,克服了其易于陷入局部最优的问题。可以看到,两种元启发式算法的融合较单一启发式方法拥有更好的性能优势。本文将融入遗传算法和粒子群算法的优势,设计适用于云环境中的工作流调度算法,并针对性能进行分析。
2 工作流模型和云资源模型
一个工作流W可以表示为有向无环图DAG,表示为W=(T,E),T表示工作流的任务集合,即T={T1,T2,…,Tn},E表示工作流中的边集合,即Ei,j=(Ti→Tj),边代表任务Ti与任务Tj间的执行约束,表明Tj无法开始执行直到任务Ti完成为止。
考虑拥有m台虚拟机资源的IaaS云模型用于部署工作流的执行任务。假设云服务器拥有足够的可用资源部署任务请求的虚拟机VM数量。需要说明的是,工作流的执行不仅带来任务的执行时间,而且会带来依赖任务间的通信时间。假设若依赖任务分配至相同的虚拟机资源上执行,则其任务间的通信时间为零。每个任务的执行时间在性能不同的虚拟机资源上是不同的,可将其表示为期望时间矩阵的形式,即
(1)
其中,1≤i≤n,1≤j≤m,ETCi,j代表任务Ti在虚拟机VMj上的估计执行时间。
虚拟机间的通信时间可表示为通信开销矩阵CO,由于两个依赖任务若分配至相同虚拟机上时的通信时间为零,故CO矩阵的对角元素上的取值均为零,具体可表示为
(2)
其中,COk,l表示在虚拟机VMk上执行的任务与在虚拟机VMl上执行的任务间的通信时间开销。
3 问题定义
为了使工作流调度更加贴合现实云计算环境,以下借鉴Amazon EC2(弹性计算云)的特征对算法的使用场景作一些假设和约束:
(1)一个虚拟机对之间的上行链路和下行链路的通信时间可能不同,并表示为VMk↔VMl,符号↔表示两个虚拟机上执行的两个依赖约束任务间数据传输的上行链路和下行链路;
(2)提供虚拟机时不可忽略虚拟机的初始启动时间,释放租用的虚拟机时不可忽略虚拟机的关机时间。
本文设计的调度算法将考虑工作流的执行跨度makespan和虚拟机上的负载均衡因素,以下对两个性能参数作出定义:
定义1执行跨度makespan(MS)。执行跨度描述为整个工作流执行完成消耗的时间。假设一台虚拟机正在进行数据传输时无法执行任务,则执行跨度makespan可表示为
MS=VM_Boot_Time+ max(VM_On_time(VMj)+VM_Shutdown_Time)
(3)
其中,j∈{1,2,…,m},VM_On_time(VMj)表示虚拟机VMj完成其调度的所有任务需要的总时间,VM_Boot_Time为虚拟机的启动时间,VM_Shutdown_Time为虚拟机的关机时间。
定义2负载均衡LB。负载均衡定义为在所有可用虚拟机上分配任务执行的前提下,所有活动虚拟机拥有均衡的负载量。通常,负载可以以虚拟机完成其调度工作流任务的实际工作时间AWT表示。如果负载等同于所有虚拟机负载之和,则所有虚拟机间的负载变化将会更小。为了衡量每台虚拟机的负载间的变化,可以计算虚拟机的实际工作时间AWT的标准方差值SD。因此,可以通过最小化AWT的标准方差SD的方式,最大化虚拟机的负载均衡度LB。虚拟机的实际工作时间AWT定义为
(4)
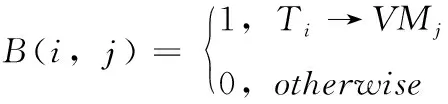
(5)
为了计算标准方差SD,需要得到所有虚拟机的AWT的平均值,计算为
(6)
因此
(7)
当SD被最小化时,负载均衡度被最大化。因此,负载均衡度LBF可以重定义为
(8)
若所有虚拟机的负载标准方差SD为零,则LBF为100%,这表明所有虚拟机上的负载分布是完全平均的。
以下对本文的工作流调度算法的优化目标作出定义和形式化描述。给定m台活动虚拟机集合VM={VM1,VM2,…,VMm}和n个任务构成的工作流T={T1,T2,…,Tn},调度算法的目标是将所有任务调度至可用的虚拟机上,并使得式(3)定义的执行跨度MS最小化,以及式(8)定义的负载均衡度LBF达到最大化。由于LBF的最大化表明标准方差SD的最小化(式(7)),因此,最优化问题可表示为执行跨度MS和标准方差SD的线性组合的最小化问题,形式化为
minz=α×MS+(1-α)×SD
(9)
约束条件为:
(2)0≤α≤1。
其中,B(i,j)由式(5)定义,约束条件(1)确保每个任务必须调度至唯一的一台虚拟机上执行,约束条件(2)的α表示在执行跨度和负载均衡度间的权重因子。
4 算法设计
工作流调度算法的基本思想如下:首先随机生成一个初始粒子种群,然后在初始粒子种群中使用粒子群优化算法PSO进行粒子进化,并且应用遗传算法GA中的交叉和变异操作在粒子群算法的第一次迭代过程中。而在每次迭代中,首先应用粒子群优化PSO的所有步骤,并标识出当前种群中的最优粒子Gbest。算法的具体步骤如下:
步骤1粒子表示。算法将一个粒子表示为任务在虚拟机上的一种调度解方案,即一个粒子可表示为
Pi=[Xi,1,Xi,2,…,Xi,n-1,Xi,n]
(10)
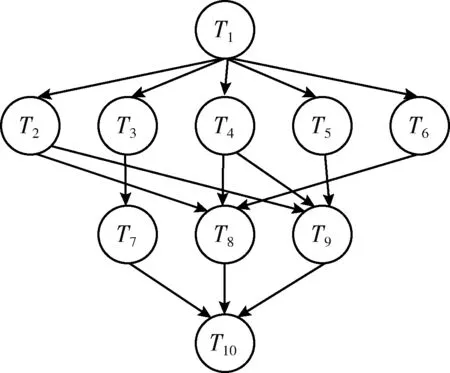
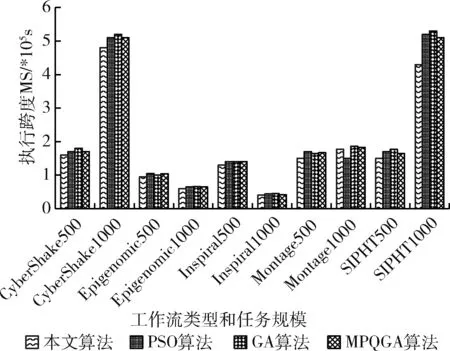
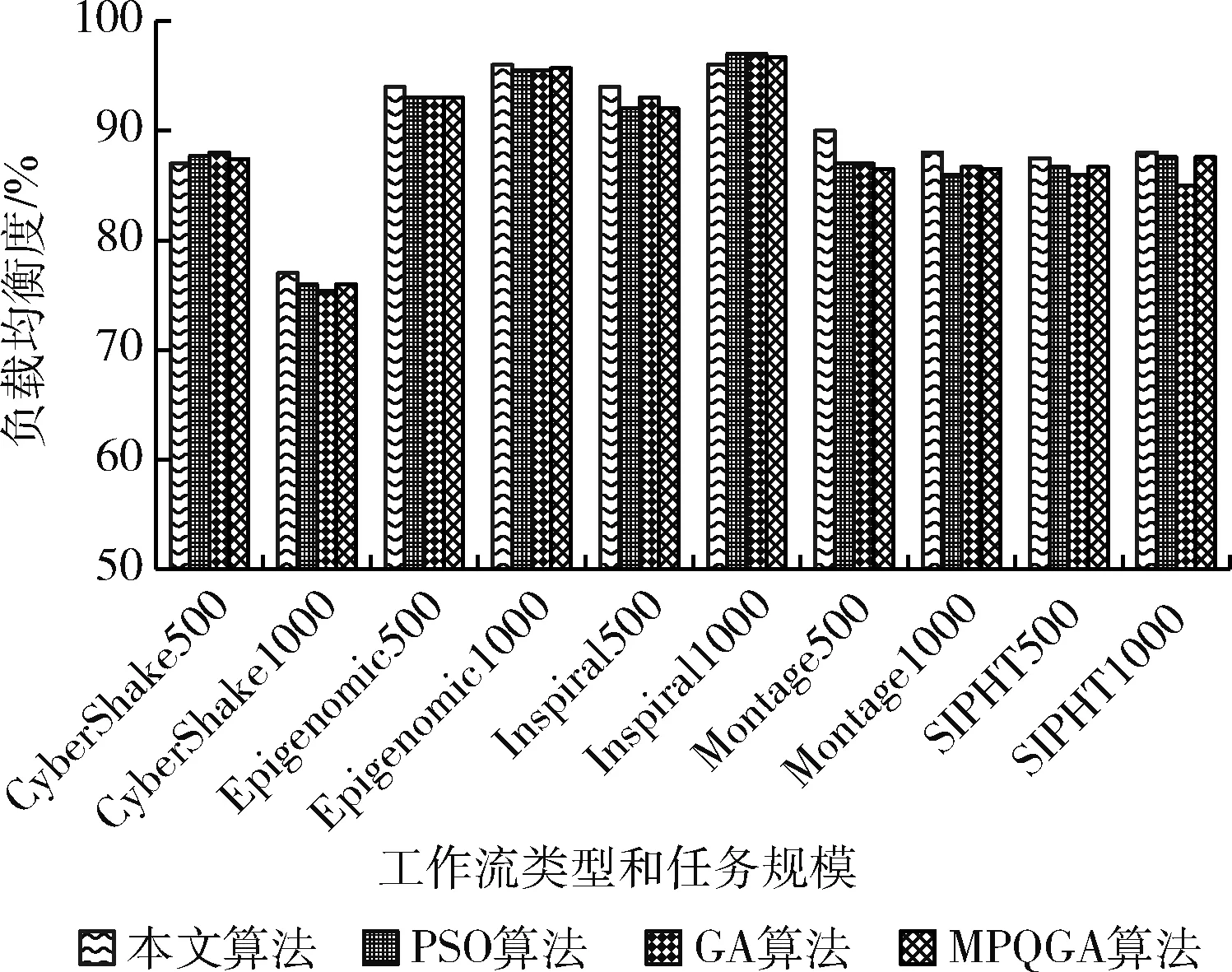
其中,Xi,t表示粒子Pi在第t维度上的位置。由于给定工作流的任务数量一定,所以所有粒子的维度是相同的。以区间(0,1]内的随机数初始化粒子的每个维度Xi,t,0 (11) 其中,m表示虚拟机的数量。如果MAPi,t=k,则任务t调度到虚拟机k,即Tt→VMk。 步骤2粒子位置和速率更新。每次迭代中,每个粒子的位置和速率分别根据式(12)和式(13)进行更新。一些粒子维度t上速率和位置的更新值可能不在区间(0,1]内(由更新等式决定)。本文的处理场景中,每个维度上粒子的位置必须满足边界条件;否则,任务将被调度至不可用的虚拟机上。为了克服以上问题,通过式(14)更新粒子的速率和位置 Vi,t(k)=w×Vi,t(k-1)+c1×r1×(XPbest,t(k-1)-Xi,t(k-1)) +c2×r2×(XGbest,t(k-1)-Xi,t(k-1)) (12) Xi,t(k)=Vi,t(k)+Xi,t(k-1) (13) 其中,r1和r2表示两个处于区间[0,1]内的随机常量,c1和c2表示加速因子常量,w表示惯性权重 (14) 粒子更新位置之后,算法针对得到的调度方案来评估每个粒子的适应度函数。如果粒子当前的适应度值优于其最优个体Pbesti的适应度,则其个体最优Pbesti以自身进行替换。因此 (15) 步骤3遗传选择和交叉。该操作中,选择两个粒子,一个为当前种群中的全局最优粒子Gbest,另一个为当前种群中的一个随机粒子。然后,通过执行单点交叉(交叉点随机选择)生成两个子代粒子,得到两个新的调度解。 步骤4遗传变异。遗传算法的变异操作的目标是维持种群粒子的多样性。变异操作可以避免子代粒子变得过于与父代粒子相似,而避免陷入局部最优解上。对于子代childi的变异,随机选择childi的两个下标j和k,使得任务j和任务k无法映射至相同的虚拟机上执行。然后,交换所选下标的值得到一个新的变异子代。 步骤5适应度评估。式(9)定义的目标函数可用于评估粒子所对应的调度解的质量。拥有更小的目标函数值的解将被优先选择。因此,目标函数即可作为适应度函数对粒子进行评估。评估粒子i的适应度函数为 F(Pi)=α×MSi+(1-α)×SDi (16) 同时需要注意的是,粒子群算法中的粒子和遗传算法中的染色体将拥有以上相同的适应度函数,这样可以在统一的基础上对种群对应的调度解进行评估。 算法1和算法2给出了本文提出的工作流调度算法的具体实施步骤,表1给出了算法描述中所应用的符号说明。算法1为工作流调度算法的主体,算法将代表工作流结构的有向无环图DAG、期望时间矩阵ETC以及通信时间矩阵CO作为算法的输入,并输出工作流调度方案。算法1将调用算法2,目的是通过调用交叉和变异函数生成两个子代粒子的方式执行遗传算法的步骤。然后,算法寻找当前种群中的最差粒子,以便以生成的最优子代粒子将其替代。而替换操作仅在子代粒子的适应度更优时才进行替换。 表1 主要符号说明 算法选择将粒子群优化算法PSO的步骤和遗传算法GA的步骤进行融合的理由如下:PSO具有易于陷入局部最优的不足,而该不足可以通过利用GA的交叉和变异操作来弥补,由于这两种操作可以为粒子带来更多的随机性。需要注意的是,交叉操作发生在全局最优Gbest与随机选择的粒子间,这样由于Gbest的参与可以得到更好的结果(即粒子和染色体)。利用遗传算法的交叉和变异操作之后,种群个体通过以最优的子代染色体替换最差粒子的方式使种群得到了过滤。通过算法1和算法2得到了任务与虚拟机间的映射方案之后,算法3将以最小化的执行跨度MS和最大化的负载均衡度LBF从种群中选择出最终的最优解。 算法1:工作流调度算法 (1)Input: workflowW,ETCmatrix,COmatrix (2)Output:Task-VM mapping (MAPi,t) (3)initialize populationPOPrandomly of sizePop_size (4)Pbesti=Pi (5)Gbest=Pk (6)forIteration=1 tomax_iterationdo (7) fork=1 toPop_sizedo (8) update velocity and position ofPk (9) calculateF(Pk) (10) updatePbestk (11) end for (12)Gbest=Pk (13) update_by GA(POP,Gbest) (14)end for (15)obtain the mapping as encoded by theGbestparticle (16)returnMAPi,t 算法1的步骤详细说明:步骤(1)进行算法输入,包括工作流结构W、任务的期望执行时间矩阵ETC和通信时间矩阵CO,步骤(2)输出最终生成的任务与虚拟机的映射调度关系。步骤(3)初始化粒子种群集合,步骤(4)和步骤(5)分别得到当前种群中的局部最优粒子和全局最优粒子,粒子Pk的适应度值为所有种群粒子中局部最优粒子适应度最小的粒子,即 步骤(6)~步骤(14)进行粒子搜索过程的若干次迭代。步骤(7)~步骤(11)在种群中的每个粒子上进行循环,其中,步骤(7)通过式(12)和式(13)更新粒子Pk的速率和位置,步骤(8)计算粒子Pk的适应度值,步骤(9)通过式(15)更新全局最优Pbestk。步骤(12)进一步将满足以下条件的粒子Pk定义为全局最优 步骤(13)在所有粒子集合和当前得到的全局最优Gbest的情况下调用遗传算法的执行过程,即算法2。步骤(15)得到由Gbest定义的编码的映射调度解,最后在步骤(16)返回映射解MAP。 算法2:Update_by GA(POP,Gbest) (1)r=random()×Pop_size (2)crossover(Pr,Gbest) to produce two childrench1andch2 (3)ch3=mutation(ch1),ch4=mutation(ch2) (4)best_child=chk (5)worst_fit=0 (6)fori=1 toPop_sizedo (7) ifworst_fit (8)worst_fit=F(Pi) (9) worst_particle=i (10)end if (11)end for (12)ifF(best_child) (13)Pworst-particle=best_child (14)end if 算法2步骤详细说明:步骤(1)通过随机生成的方法得到一个粒子的下标(r值需要取整),步骤(2)在粒子Pr与当前的全局最优粒子Gbest间进行遗传交叉操作,生成两个子代粒子ch1和ch2。步骤(3)在子代粒子ch1上进行遗传变异操作得到新的子代ch3,在子代粒子ch2上进行遗传变异操作得到新的子代ch4。步骤(4)将满足以下条件的子代定义为当前的最优子代粒子 步骤(5)初始化最差粒子适应度为0,步骤(6)~步骤(10)在所有粒子上进行迭代循环,步骤(7)判断当前粒子Pi的适应度值大于worst_fit,则在步骤(8)将粒子Pi的适应度赋值为最差适应度值,在步骤(9)将当前粒子定义为最差粒子,该循环过程即是在所有粒子集合中寻找适应度最大(性能最差)的粒子。步骤(12)判断生成的4个子代粒子中适应度最小(性能最好)的粒子的适应度与找到的最差适应度粒子间的适应度的大小关系,若子代的适应度更小,则在步骤(13)中将其定义为最差粒子。 算法3:计算工作流执行跨度MS (1)Input:workflow W,mappingMAPi,t,ETCmatrix,COmatrix (2)Output:makespanMS (3)for eachVMj∈VMdo (4)VM_On_time[VMj]=0 (5)end for (6)for each taskTi∈Win the topological order do (7) ifTi.Pre_Count!=0 then (8) Pre_finish_time=maxTp∈Pre(Ti)(Task_actual_finish_time[Tpi]) (9) end if (10) ifTi.Succ_Count!=0 then (11) Data_Transfer_time=0 (12) for each taskTj,Tj∈Succ(Ti) &MAP[i]≠MAP[j] do (13) if the output data is not transferred toVMMAP[j] from the taskTithen (14)Data_Transfer_time=Data_Transfer_time+COi,j (15) end if (16) end for (17) end if (18) execution time of taskTionVMj=ETCi,j (19)actual_start_time(Ti)=max(Pre_finish_time,VM_On_time[MAP[i]] (20)actual_finish_time(Ti)=actual_start_time(Ti)+ETCi,j+Data_Trans_time (21)VM_On_time[MAP[i]]=actual_finish_time(Ti) (22)end for (23)MS=VM_boot_time+VM_On_time[VMj]+VM_shudown_time (24)return makespanMS 算法3的步骤详细说明:步骤(1)进行算法输入,包括工作流结构W、算法1计算得到的调度解MAP、任务的期望执行时间矩阵ETC和通信时间矩阵CO,步骤(2)输出整个工作流任务执行的时间跨度。步骤(3)~步骤(5)将所有虚拟机的执行时间初始化为0,步骤(6)~步骤(22)在工作流中的所有任务上进行迭代循环,其中,步骤(7)~步骤(9)判断:若当前任务的前驱任务集合不为空,则将其前驱的完成时间定义为所有前驱任务集中任务实际完成时间的最大值。步骤(10)~步骤(17)更新任务间的数据传输时间,其中,步骤(10)判断若当前任务的后继任务集合不为空,则在步骤(11)将数据传输时间初始化为0,步骤(12)~步骤(16)在所有当前任务的后继任务集合中进行循环迭代,若当前任务的输出数据未传输至映射解中对应的虚拟机上,则在步骤(14)更新数据传输时间。步骤(18)得到当前任务的执行时间,步骤(19)更新当前任务的实际开始时间为前驱任务完成时间与映射虚拟机的运行时间的较大值,步骤(20)计算当前任务的实际完成时间为任务开始时间、任务在映射虚拟机上的执行时间及数据传输时间之和,步骤(21)更新调度当前任务的虚拟机的运行时间为其实际的完成时间,步骤(23)则通过虚拟机的启动时间、虚拟机的运行时间以及虚拟机的关机时间之和得到整个工作流的执行跨度时间,最后在步骤(24)将执行跨度返回。 考虑图1的工作流结构,由10个任务组成,3个虚拟机集合VM用于任务的执行与调度,表示为VM={VM1,VM2,VM3}。图1下方矩阵同时给出了ETC矩阵和CO矩阵。 图1 示例工作流 令种群规模为5,以区间(0,1]内随机值对种群中每个粒子初始化,随机生成的初始种群矩阵POP见表2。利用式(11)可以计算每个粒子所对应的任务与虚拟机间的映射解,即MAP矩阵,表3所示即为利用式(16)计算得到的每个粒子的适应度值。MAP2,5=3表明粒子P2提供的调度解中,任务T5调度至虚拟机VM3上执行。由于粒子P1拥有最小的适应度值,因此将其作为当前种群的全局最优粒子Gbest,见表4。 表2 初始粒子种群 表3 粒子代表的映射解 表4 初始阶段的Pbest和Gbest的适应度值 以下是当前迭代过程中的剩余算法步骤: 步骤1利用式(12)和式(13)对应Gbest和Pbest更新粒子位置,即表5所示结果。 表5 粒子位置更新 步骤2利用式(11)和式(16)计算对应于更新粒子的适应度值F(Pi),对应的MAP矩阵见表6。 表6 粒子更新后的映射解 步骤3利用式(15)更新Pbesti,寻找种群中的Gbest和最差粒子。P1为当前种群中的全局最优粒子,P5为最差粒子,见表7。 表7 第1轮迭代后Pbest的适应度值 步骤4随机选择任意粒子与全局最优粒子Gbest执行交叉操作,生成两个子代粒子child1和child2。 步骤5计算生成子代粒子的适应度值,结果见表8。 表8 子代粒子的映射 步骤6两个子代粒子进行变异操作,变异后,两个子代粒子的适应度值分别为96.72和87.89。 步骤7变异后子代child2的适应度值得以改进,因此,将变异子代child2保留在种群中,子代child1不作变异。 步骤8两个子代粒子中,child1为最优粒子,且比当前种群中的最差粒子P5更优,因此,以child1替换粒子P5。重复以上步骤直到达到最大迭代次数。最终的调度解见表9。 表9 最优的任务-虚拟机映射解 为了评估算法性能,本节设计仿真实验对算法进行测试。使用5种不同科学领域中的合成工作流结构作为数据源[19],包括:①Montage工作流:天文学;②Epigenomic工作流:生物学;③CyberShake工作流:地震学;④Inspiral工作流:引力物理学;⑤SIPHT:生物信息学。图2给出5种科学工作流的结构模型。5种工作流结构在其结构特征和任务并行程度等方面均体现出不同特征,在此环境下的测试有利于观察算法在不同结构组成的工作流中性能的适应性和稳定性。Montage工作流为天文学领域中的工作流形式,任务以I/O密集型为主,对CPU计算能力要求不高,Inspiral工作流为物理学领域引力波工作流形式,任务以计算密集型为主,且对内存要求较多,Epigenomics工作流为信息生物领域的工作流形式,任务以计算密集型为主,且对内存要求较多,CyberShake工作流为地震学领域的工作流形式,任务以数据密集型为主,且对计算能力和内存存储均有较高要求。利用CloudSim作为仿真工具包[20],现有的CloudSim工具包仅允许调度独立任务,不适用于多个相互关联的依赖任务组成的工作流调度问题。因此,笔者对CloudSim的内核架构进行扩展。 图2 测试的5种科学工作流结构 表10给出仿真实验中算法涉及参数,w为惯性权重,处于区间[0,1]内,c1和c2为加速因子,用于控制粒子在搜索空间中的加速度,r1和r2为(0,1]内的随机生成数,每台虚拟机的启动时间和关机时间均设置为0.5 s。选择同样的元启发式调度算法PSO-WS[5]、GA-WS[15]以及MPQGA[20]算法进行性能的对比。 表10 实验参数 所有算法仿真均在相同仿真环境和相同参数设置进行,比较的性能指标包括工作流的执行跨度、负载均衡度以及算法得到的调度对应的适应度值,比较结果分别如图3~图5所示。每个图中的数据设置工作流任务为500和1000,虚拟机数量对应为50台和100台,并在5种不同的科学工作流结构类型中得到的结果。从图3可以观察到,本文算法在所有工作流类型和所有任务规模下得到比其它算法更低的执行跨度,且在所有任务规模下对于执行跨度的改进是比较充分的,这说明融合式的元启发式调度算法在调度解寻优上是有效可行的,能够寻找到更优的调度解,有效提高调度效率。对于图4所示的负载均衡度的性能指标,可以看出在500个任务的CyberShake工作流和1000个任务的Inspiral工作流上的负载均衡并没有其它算法表现得更好,然而,在其它工作流类型和任务规模下,本文算法的负载均衡表现依然是最好的,且在不同任务规模的所有其它工作流类型上,本文算法在负载均衡度上也得到了很好的改进。图5是兼顾考虑执行跨度和负载均衡因素下调度解所对应的适应度值的情况,它可以衡量调度解的质量。可以看到,本文算法的适应度值表现得比其它算法更好,即使在CyberShake工作流中执行跨度出现了更高的值,这说明在两项性能指标的均衡性上,本文算法得到的调度解是更优的。 图3 执行跨度性能 图4 负载均衡度性能 图5 适应度性能 针对云工作流调度问题,提出了一种融合遗传算法和粒子群优化算法的工作流调度负载均衡算法。算法可以充分利用多元启发式方法融合的优势,避免遗传算法的过慢收敛和粒子群算法易于陷入局部最优的缺陷,有效将工作流任务映射至虚拟机资源上,实现全局工作流执行跨度的最小化和虚拟机分配负载的均衡。在现实科学工作流的仿真测试下,验证了算法性能。与几种单一元启发式工作流调度方法相比,验证新的算法拥有更高的执行效率和负载均衡度。进一步研究将集中在其它性能指标的考虑上,如何降低工作流执行过程中虚拟机资源上的能耗开销,以及如何考虑虚拟机资源的运行可靠性从而将工作流任务调度的安全性因素考虑进来,进一步提出融合元启发式方法的多目标化的工作流调度算法。
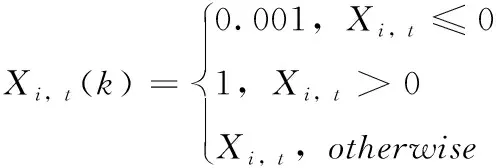
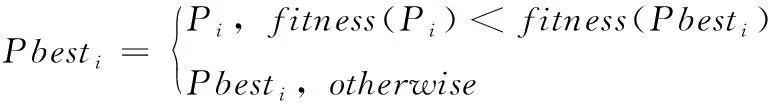

5 算例说明
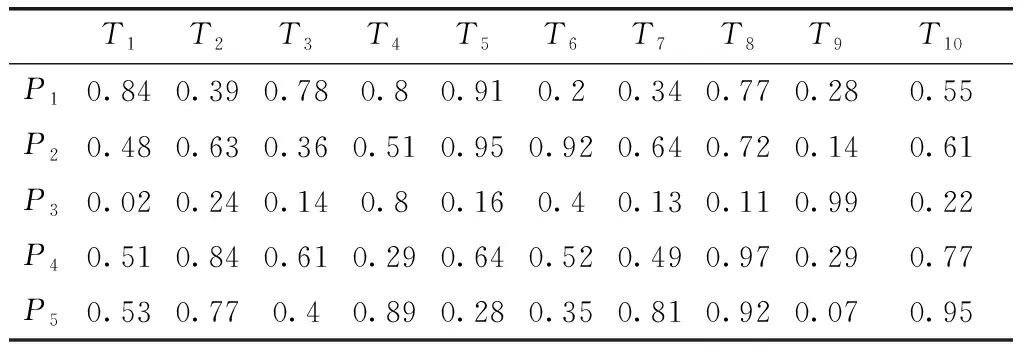



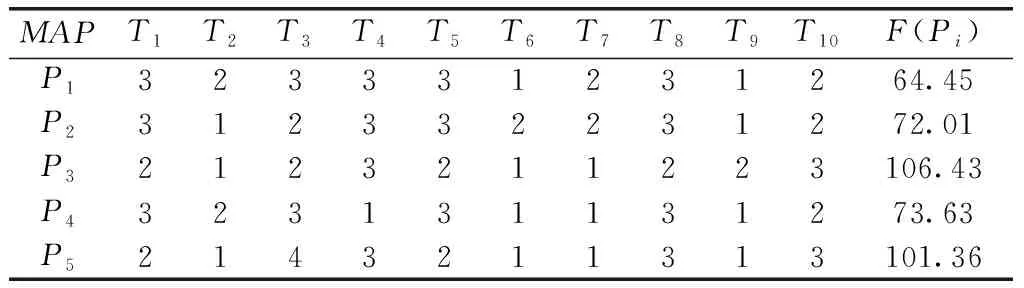



6 实验仿真
6.1 仿真环境搭建
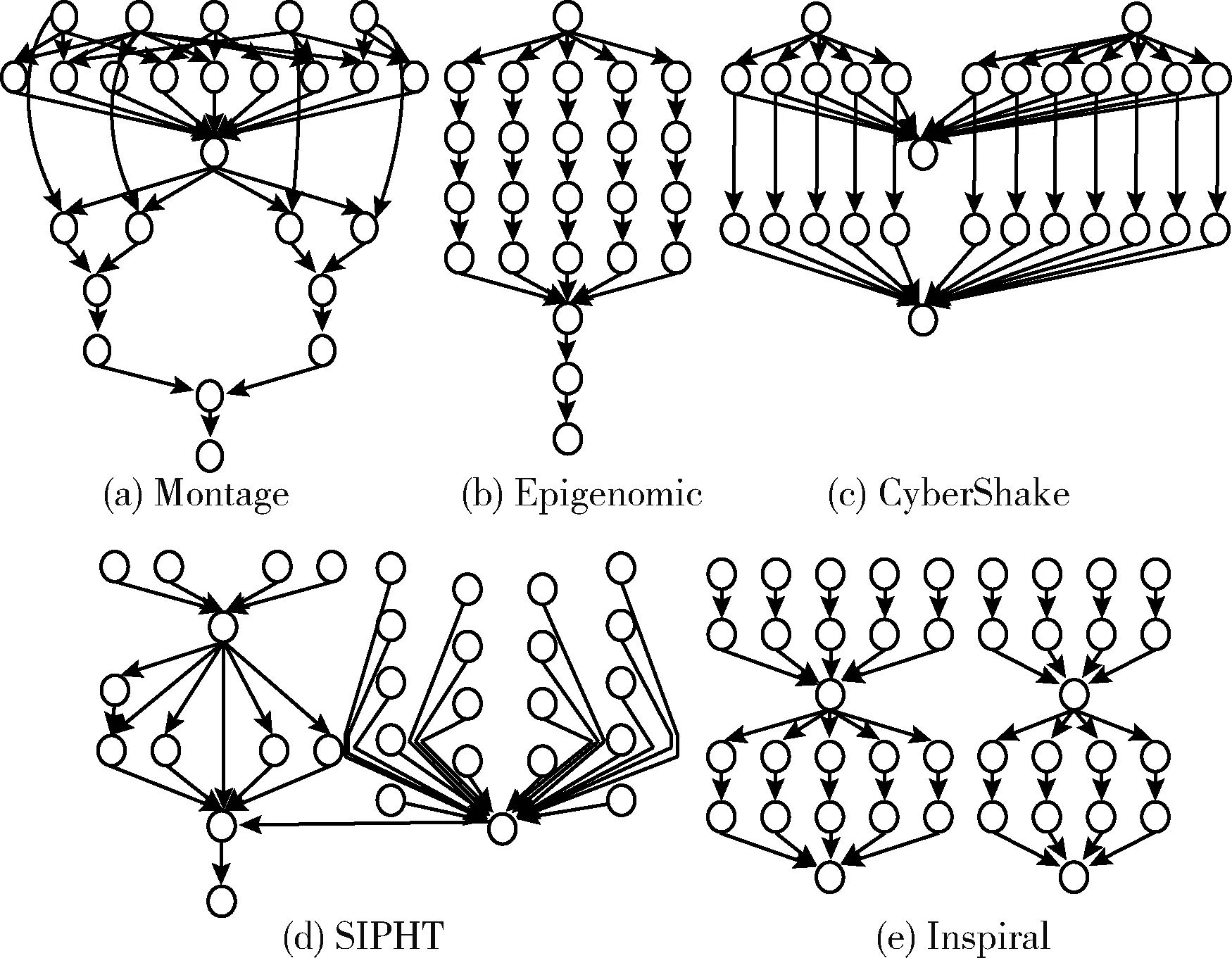
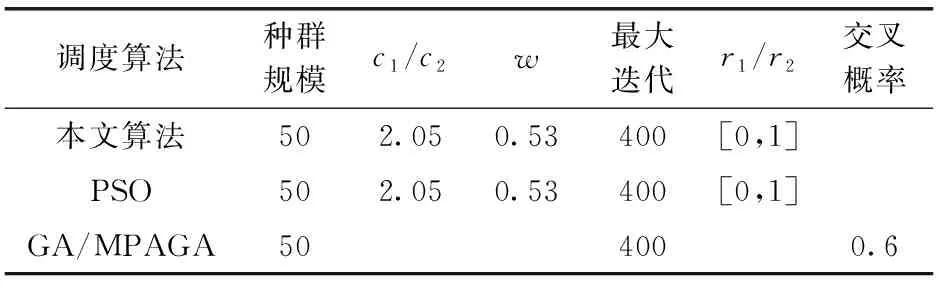
6.2 结果分析

7 结束语
