一二次融合的智能集成开关在配电网上应用的研究

王立永, 李晖, 吴红林, 丁冬, 佘妍

(国网北京市电力公司, 北京 100031)

0 引言

目前，电力用户越来越重视电网建设，对配电网的自动化、智能化要求也越来越高。在配电网系统运行过程中，越来越多地应用到一二次融合智能集成开关[1]。但是由于电网环境的复杂性和不确定性，一二次融合智能集成开关在工作过程中容易出现故障[2]，比如受电网环境中开关打开、开关闭合、闸刀分开、闸刀闭合、设备带电、设备不带电、电压含量、电流含量、功率参数、转速数据、汽温参数、汽压参数、流量参数、真空度、设备温湿度、温升、温降等因素影响[3]。因此，对一二次融合智能集成开关的检测就成为亟待解决的技术问题。

经过技术的发展，研究出多种集成开关检测技术，其中文献[1]利用参数估计法用来检测集成开关在配电网应用的灵敏程度，通过具体参数能够更加精确地了解集成开关的运行状态。但是这种方法运行不够稳定，容易导致系统失稳现象[4]。文献[2]利用等价空间法使集成开关融入到配电网系统中，这可以解决集成开关的兼容性问题，使配电系统更加稳定，但是这种方法技术要求较高，不具有普遍性[5]。

基于上述技术难题，本文通过EMD-ICA融合技术对集成开关运行状态信息提取，然后采用BP神经网络算法模型对电网故障进行诊断，从而保证集成开关的灵敏度，而且能够解决集成开关检测误差较大的问题。

1 故障信息提取和分析模型

本研究采用EMD-ICA技术实现电力配电网中故障信息的提取，并利用BP神经网络算法模型实现一二次融合智能开关的故障诊断，模型分析构架如图1所示。

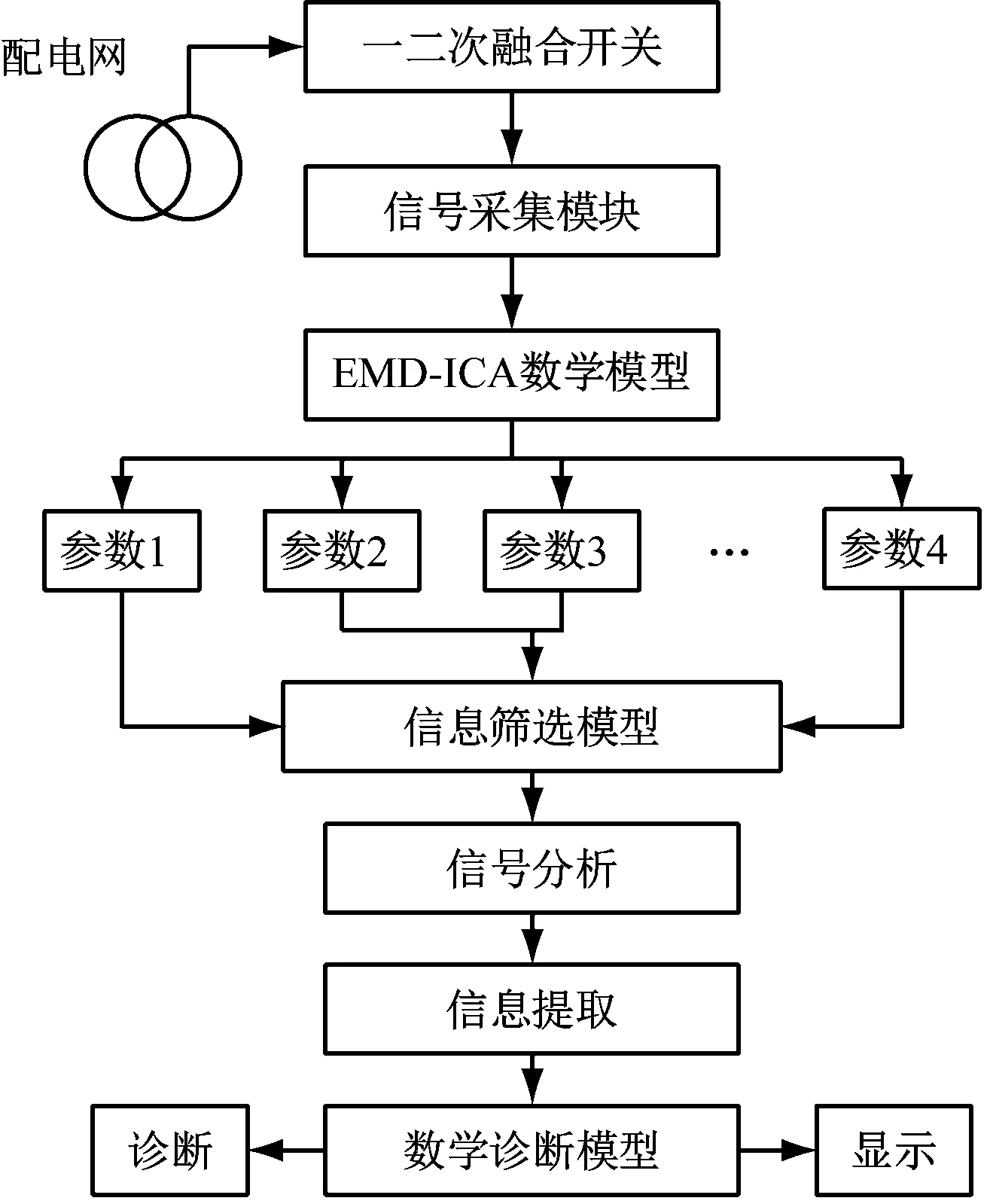
图1 智能集成开关应用示意图

在应用过程中，通过信号采集模块采集一二次融合开关在配电网上的故障信息，然后构建EMD-ICA(经验模态分解Empirical Mode Decomposition，EMD；独立分量分析Independence Component Analysis，ICA)数学模型，通过该模型，输出诸多的故障信息独立分量，在应用时，将这些输出的独立分量的故障信息能量值输入至BP神经网络网络数学诊断模型，通过反复训练、诊断，显示出最精确的故障信息[6]。

1.1 EMD-ICA融合算法

在进行故障提取时，EMD方法能够对配电网中存在的非线性、非平稳一二次融合智能开关故障信号进行处理。在对故障信息进行分解的期间，从信息采集模块采集到的信息中，能够快、准、自动地输出基函数，并且获取高分辨率数据信息，便于用户分析、研究[7]。将ICA 算法融入EMD算法集成为一个数学模型，实现配电网环境下一二次融合智能开关应用过程中的数据分解、去噪和故障信息特征分离，将信号的时域、频域和能量特征参数一起提取出来[8]。

EMD-ICA融合算法首先假设采集到的一二次融合智能开关的原始信息为X(t)，设其最小值为Xmin(t)，最大值为Xmax(t)，采用曲线插值算法对最大值和最小值进行拟合计算，得出平均包络m1(t)，表示为式(1)。

(1)

然后进一步计算，则有式(2)。

d1(t)=X(t)-m1(t)

(2)

其中,d1(t)为剩余信号。对该信息进行进一步地处理，当门限值大于筛分门限值(SD)时，可以得出第一阶模态分量c1(t)，也可以称为第一IMF，在具体实施例中，筛分门限值为介于0.15-0.25之间的值[9]。其中SD的求值式可以表示为式(3)。

(3)

继续计算第一阶残差量r1(t)，表示为式(4)。

r1(t)=X(t)-c1(t)

(4)

然后对上述算法反复进行计算，假设经过n次计算后，可最终获取第n阶模拟函数cn(t)、最终符合标准的残差量rn(t)。通过EMD算法分解后，得出表达式为式(5)。

(5)

根据式(5)计算结果，在配电网工作环境的干扰下，集成开关的信息采集更加困难，采用EMD-ICA融合算法能够更加方便将集成开关参数信息从这些混合信号中提取出来[10]，其原理结构如图2所示。

图2 EMD-ICA融合算法原理框图

在工作时，假设配电网中一二次融合的智能集成开关的故障源信号S经过混合矩阵A计算，输出的数据信息为X，再经过解混矩阵B计算，输出独立分量Y，也可以称为从信号输出X的中分离的独立分量。利用上述方法进行多次对比分析，求出独立分量Y的最优值[11]。在本文研究中，将最逼近S的独立分量Y称为最优值。因此，需要借助于统计独立学用户原理来实施这种算法，同时，还要选择适当的目标函数，然后反复计算，根据均方差计算方法，最终得出最优的故障信息目标函数[12]。

1.2 故障信息分析

在利用上述算法提取出故障信号后，在采用BP神经网络算法模型对采集到的故障信息进行诊断。BP神经网络算法模型的学习能力比较强，具有较强的自组织性，从工作效率、学习精度都优于其他故障诊断算法[13-15]。比如，利用该模型对多种类型的一二次融合的智能集成开关进行故障诊断，BP神经网络算法模型中的一个输出节点对应一种类型的故障信息。当多个故障节点的信息值与理想输出值比较逼近时，则可以同时诊断出多个故障类型，进而实现配电网中运行的一二次融合的智能集成开关的精确判断[16-17]，BP神经网络算法模型如图3所示。

图3 BP神经网络算法模型示意图

在图3中，假设通过EMD-ICA算法模型提取出的故障信息数据集记做为{X1,X2,…,Xn}，然后为该数据集寻找目标数据W*，然后将f(W*Xi)*Xi最大程度地逼近BP神经网络算法模型输出数值Yi，将f记为激励函数[18]。则基于BP神经网络算法模型的误差函数可以为式(6)。

(6)

在式(6)中，对误差e值进行调节，并将误差e值调节到最小，则这可以通过函数求导来实现，在求导函数时，令下降梯度记作为式(7)。

(7)

为了实现更高的精度和学习，通过多次误差求导，求其平均值进行计算，并且在对提取的一二次融合的智能集成开关误差数据进行反复的学习和训练中，通过多次修改权重矩阵W，这样，能够获取更好的适应值，进而获取更高的学习精度[19]。

2 运行风险评估方法

下面对一二次融合的智能集成开关运行过程中的失效概率进行评价。一二次融合的智能集成开关失效情况直接影响配电网运行的可靠性和稳定性[20]，在评价其实效性时，采用式(8)进行计算,该计算式为保护功能整体失效算法。

(8)

式中，Pk为主回路中中第k套元件的保护失效率[21];Pki为控制电路中二次设备的失效率;Pk*fj为故障信号进行分解后，主回路的保护逻辑功能的失效情况(失效率)[22]。假设在220 kV的高压配电中，主回路线路双套主保护的整体失效率可以表示为式(9)。

P=P1*P2

(9)

式中，P1表示主一设备内运行时的保护失效率;P2表示主二设备内运行时的保护失效率。

然后在对其失效概率进行评估，假设将保护全部失效概率定义为P2.1，然后定义套保护失效概率为P2.1.i，则有式(10)。

R2.1=P2.1*LE1

(10)

其中，R2.1为对保护停运的系统存在的风险进行计算的结果;LE1为一次设备中的一次元件失效的原因，产生失负荷的后果值，该值可以通过元件在不工作的情况下，在配电网中通过潮流计算，实时获得的电网信息数据值。对于配电网系统中保护误动的系统风险来说，建立数据评价模型时，在考虑配电网系统中相邻的电力设备故障时[21-22]，在第k个相邻电力设备存在故障风险情况下，可以表示为式(11)。

R2.2.k=P1.k*P2.2*LE2.2.k

(11)

式中，P1.k表示电力电网中第k个电力设备发生故障的概率;LE2.2.k表示第k个电力设备与目前正在运行的电力设备同步停运时计算得到的结果值。基于此，总的误动风险表示为式(12)。

(12)

通过式(12)可以评价一二次融合设备运行的可靠性，进而把握电力设备运行情况。

3 试验结果及分析

在试验时，由于一二次融合的智能集成开关在高压电网中工作，高压带电给人体带来很大的威胁，在试验时，通过采集光伏阵列来实现，并将试验架构分成数据采集层、数据传输层、数据处理层、数据分析层和数据应用层[23-24]，如图4所示。

图4 试验架构示意图

在计算机软件上对集成开关在配电网中的应用进行仿真，其中使用的软件系统为MATLAB2013b仿真软件，通过上述硬件构建，在MATLAB2013b软件上建立基于 Simulink-Function 的仿真模型，如图5所示。

图5 基于Simulink仿真模型图

其中,光伏阵列为5×10阵列，光伏组件的工作参数为：P=300 Wp；电压U=32.5 V；电流为9.08 A；开路电压为38.4 V；短路电流为9.62 A。在仿真图5中，仿真参数电容C1=200 μF；电容C2=500 μF；电感L=30 mH；负载R=30 Ω；载波频率PWM=30 kHz[25]。

3.1 EMD-ICA算法验证

通过数学仿真，假设从源信号输出两个正弦信号，频率值为 20、10，幅值为1。通过混合，得出波形如图6所示。

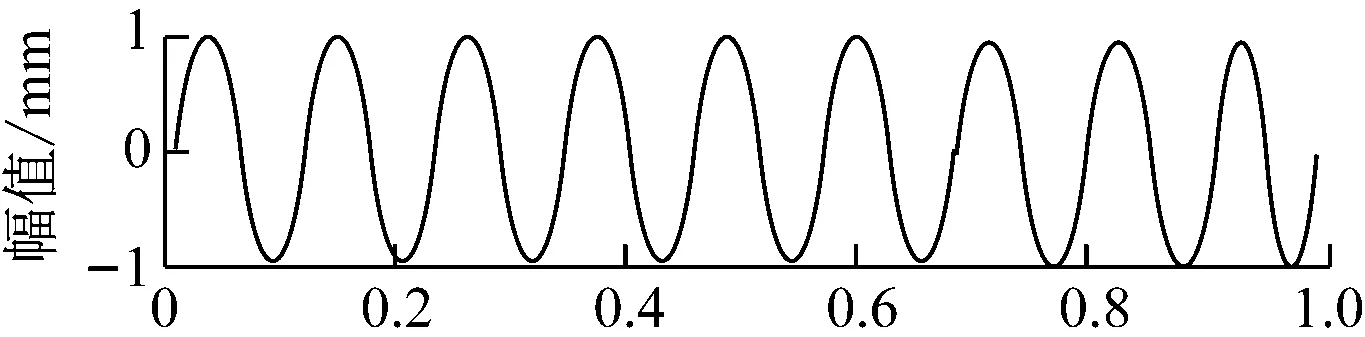
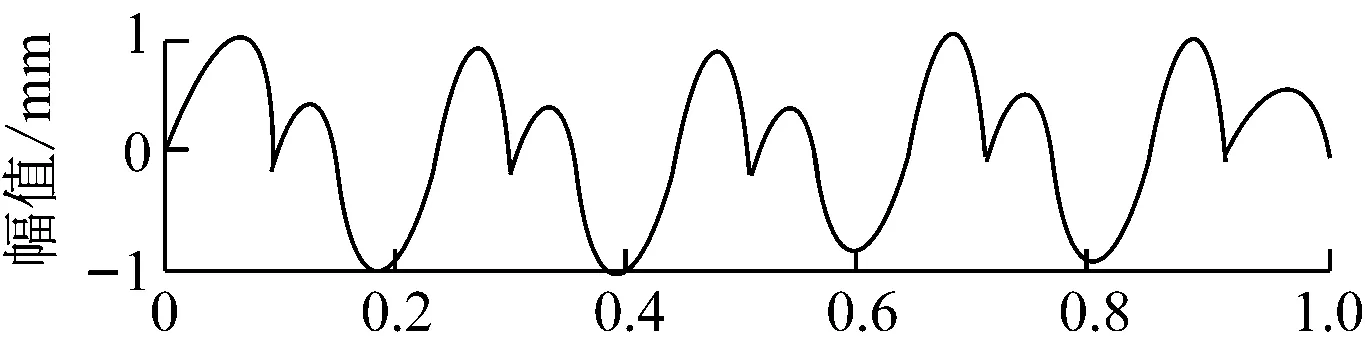
图6 源信号与混合后的波形图示意图

然后再进行EMD-ICA融合算法进行计算，在本试验中，在输出3个固有模态分量和剩余项之后，得到的独立分量如图7所示。

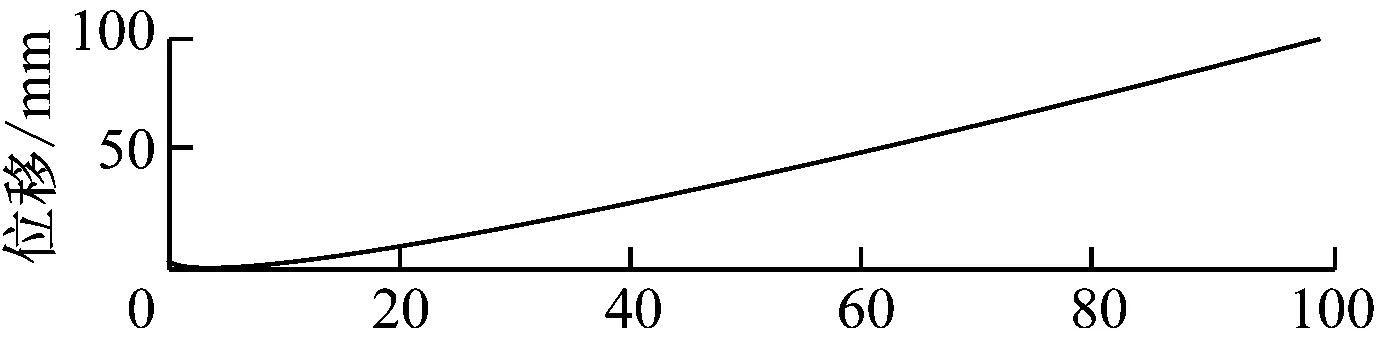
图7 独立分量波形图

通过图6、图7可以看出，应用EMD-ICA算法对采集到的原始信号处理后，分离出两个独立分量，然后再应用EMD-ICA算法分离单通道中的混合信号的独立分量，最终得出如图7所示的信息分量波形图。说明本研究的EMD-ICA算法是可行的。

3.2 BP神经网络算法验证

通过上文介绍的BP神经网络算法模型，试验步骤如图8所示。

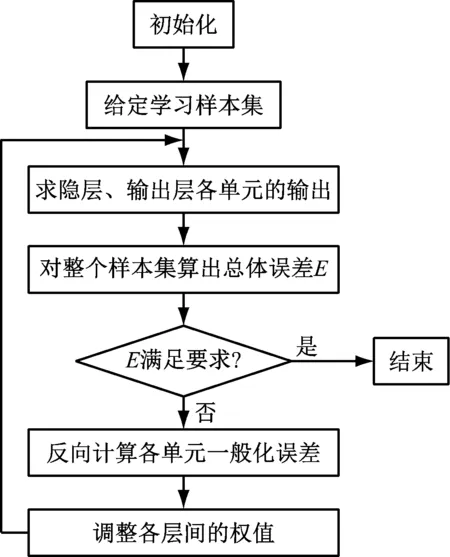
图8 BP神经网络算法结构示意图

通过采用MTALAB编程仿真，假设在试验时，采用隐层神经元数为15个 ，误差精度设定为0.001，采用50组样本数据，得出的波形如图9所示。

图9 算法比对示意图

通过上述试验，采用EMD-ICA算法之后，BP神经网络算法模型的精度更高。

3.3 运行风险评估准确度验证

在验证一二次融合的智能集成开关运行风险评估准确度时，采集到的数据如表1所示。

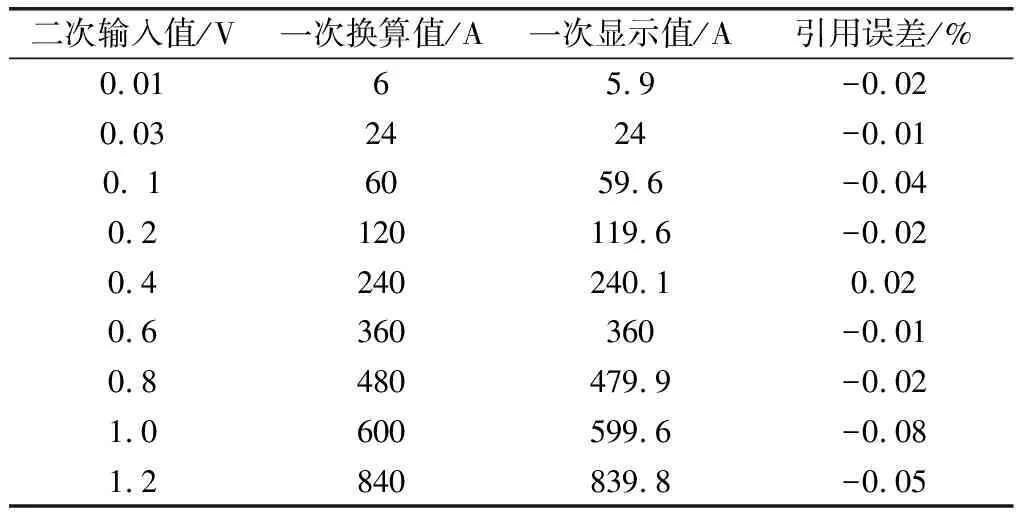
表1 A相电流采样测试数据

利用上述介绍的计算式，通过式(8)—式(12)计算其总误差，其中n表示电力电网线路中所有电力设备运行的个数。通过计算，得出的数据如表2所示。

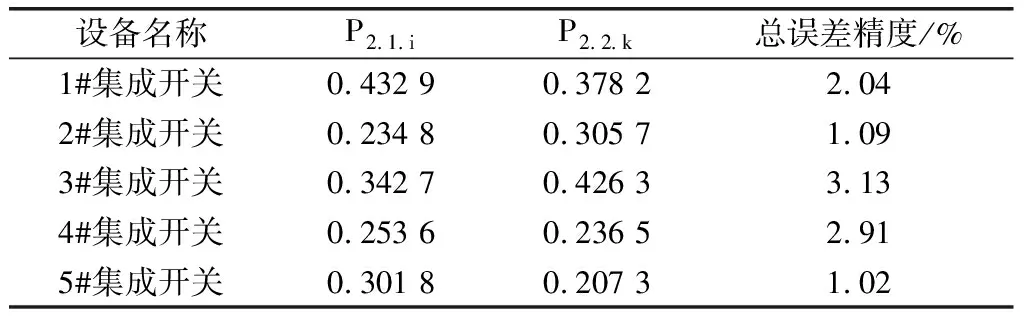
表2 计算数据表

通过上述测试，采用上文引出的计算式进行计算，总的精度误差低于5%，通过对上述参数进行评估，能够获取运行的可靠性。通过对比分析，得出的数据如表3所示。

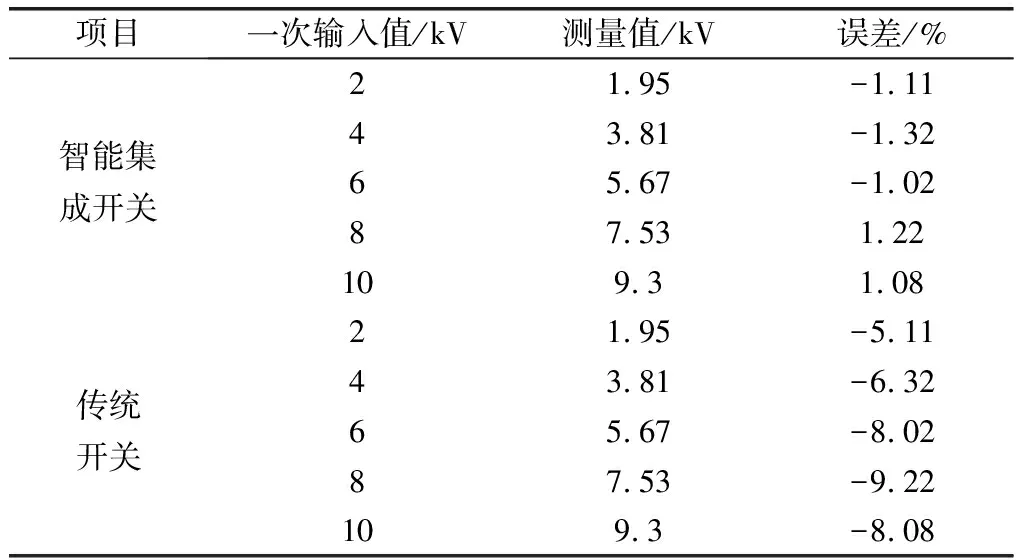
表3 试验对比数据表

通过上述比较，采用式(8)—式(12)计算出的智能集成开关具有较低的误差精度。一二次融合智能开关在数据采集方面、保护失效、误动和拒动概率等方面，都具有较低的误差精度。

5 总结

本研究通过采用EMD-ICA算法模型和BP神经网络算法模型，对电力配电网中正常运行的一二次融合智能开关进行故障信息提取和故障诊断，实现其运行状态的故障监控，又构建出运行风险评估方法对一二次融合的智能集成开关运行过程中的失效概率进行评价。试验表明，EMD-ICA算法模型融合BP神经网络算法模型具有较好的技术效果，一二次融合智能开关的风险评估方法误差精度低，具有较好的应用价值。本研究的算法为保证配电网的正常运行提供有力的保障，也为配电网的良性运行提供技术支撑。但是，一二次融合智能开关的安全、稳定运行仍旧是一个长期研究的课题，在运行过程中也将出现各种不足。