应用组合模型的高校毕业生就业率预测研究

徐永慧

(宁夏电化教育中心， 宁夏 银川 750004 )

0 引言

由于高校不断地扩招，每年毕业的大学生数量急剧增加，而企业所提供的工作岗位数量，不足以满足大学生的就业需求，使得多个学生去抢同一个岗位，就业竞争十分激烈。高等院校的招生绝大部分取决于院校的毕业学生就业率，较高的就业率可以有效提高学校的知名度和声誉。但是，由于受当下的经济环境发展态势、就业市场发展规模及毕业生自身发展情况等因素影响，其就业率具有一定的随机性和周期性，是一种复杂的非线性系统，一直是高校关注的焦点[1-3]。

当前有部分学者对高校毕业生就业率进行了研究，主要预测方法有灰色模型和BP人工神经网络等方法[4-6]，其中灰色模型是一种线性分析方法，可以有效反映当前高校毕业生的线性就业率变化特点，但是当高校毕业生就业发生随机变化时，其无法及时获取数据信息，导致高校毕业生就业率预测具有较大误差；BP神经网络虽然具有良好的非线性建模能力，但是高校毕业生的就业率具有周期性变化的特点，其无法有效获取周期内的变化特征数值，导致预测结果具有误差[7-9]。还有部分学者提出了组合模型的就业率预测方法，如多种神经网络结合、多元线性回归与模型结合等。这些组合模型在一定程度上可以有效获取精准的就业率预测结果。但是，这些组合模型没有特征分解能力，因此当就业率发生细微变化时，其无法获取精确的预测结果，这些情况使得高校毕业生就业率预测精度有待进一步提高[10-12]。

由于单一模型对高校毕业生就业率预测的精准水平不高，误差较大等问题，对此本文提出组合模型的高校毕业生就业率预测方法。采用小波分析方法，多尺度分解高校毕业生就业率数据序列，利用灰色模型确定累加序列参数，通过灰色模型和BP神经网络获取低频和高频高校毕业生就业率数据序列参数，利用误差反馈值进行建模与预测，得到相应的预测结果，实现高校毕业生就业率的精准预测。最后进行实验对比测试，得出有效性结论。

1 组合模型的高校毕业生就业率预测方法

1.1 小波分析

小波分析可以通过多尺度对复杂信号进行细分处理，对于信号x(t)，通过小波函数φ(t)进行a尺度和b偏移量的平移后，可以得到时域表达式为式(1)。

(1)

首先采用小波分析的Mallat算法对高校毕业生就业率历史数据进行细分，得到高频和低频序列参数。一般通过3-4层的细分分解，可以得到比较理想的细分结果，将这些细分数值进行重构处理，融合就业率预测结果。

1.2 灰色模型

一个高校毕业生就业率数据序列X(0)={x(0)(1),x(0)(2),…,x(0)(n)}，对其进行一次累加产生一个新的序列X(1)={x(1)(1),x(1)(2),…,x(1)(n)}，其中第k项为式(2)。

(2)

灰色模型的预测方程，具体可以写成式(3)。

(3)

式中，a，u为待定的参数。

可以解出式(3)得到式(4)。

(4)

对式(4)采用最小二乘法可以得到参数a和u。

1.3 BP神经网络

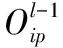
(5)

式中，w为连接权值。

第L层的第i个节点的输出为式(6)。

(6)

式中，f(·)为激励函数，具体如式(7)。

(7)

通过误差反馈对连接权值进行调整，直到精度满足实际要求为止，由此完成训练样本学习。

1.4 组合模型的高校毕业生就业率预测步骤

(1) 采集高校毕业生就业率历史数据，并通过相关专家对丢失数据进行补齐，错误的数据进行删除。

(2) 高校毕业生就业率数据具有随机性和周期性的特点，其不稳定性和时变性较强，因此对其进行归一化处理，具体如式(8)。

(8)

(3) 采用小波分析对高校毕业生就业率历史数据进行多尺度分解，得到低频的高校毕业生就业率数据序列和高频的高校毕业生就业率数据序列，其中低频的高校毕业生就业率数据序列包含了周期性变化特点，而高频的高校毕业生就业率数据序列包含了随机性变化特点。

(4) 采用灰色模型对低频的高校毕业生就业率数据序列进行建模与预测，得到相应的预测结果。

(5) 采用BP神经网络对高频的高校毕业生就业率数据序列进行建模与预测，得到相应的预测结果。

(6) 采用小波分析对低频和高频的高校毕业生就业率数据序列进行叠加，得到高校毕业生就业率最终预测结果。

综合上述可知，组合模型的高校毕业生就业率预测方法的工作流程,如图1所示。

图1 组合模型的高校毕业生就业率预测流程

2 仿真测试

2.1 高校毕业生就业率的数据来源

为了验证所提组合模型的高校毕业生就业率预测方法的有效性进行实验，拟定实验平台即MATLABR 2019 b，主频为1的环境下进行仿真实验。采集宁夏银川某高等院校2020年公开就业率数据，随机选取25个样本数据，构建模型对其进行分析，具体如图2所示。

图2 就业率时间序列数据

分析图2可知，高校毕业生就业率在一定时期内具有明显的上升或下降趋势，因此其具有周期性的特点，并且就业率的随机性较强。

2.2 预测精度对比

随机选取25个样本数据进行分类处理，将15个样本数据作为训练样本，10个样本作为检验样本。统计本文方法、BP神经网络和灰色系统对高校毕业生就业率的拟合和预测结果，具体测试结果分别如图3、图4所示。

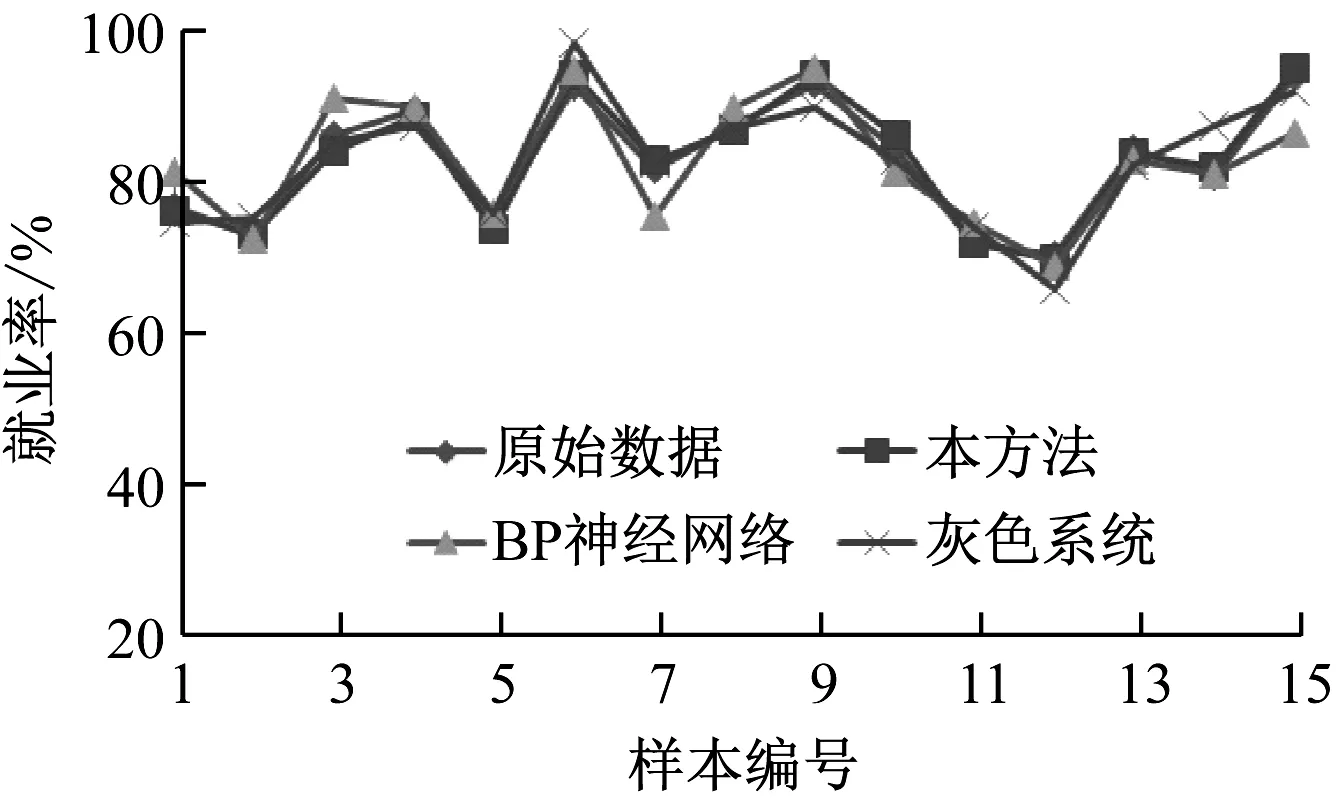
图3 高校毕业生就业率的拟合结果

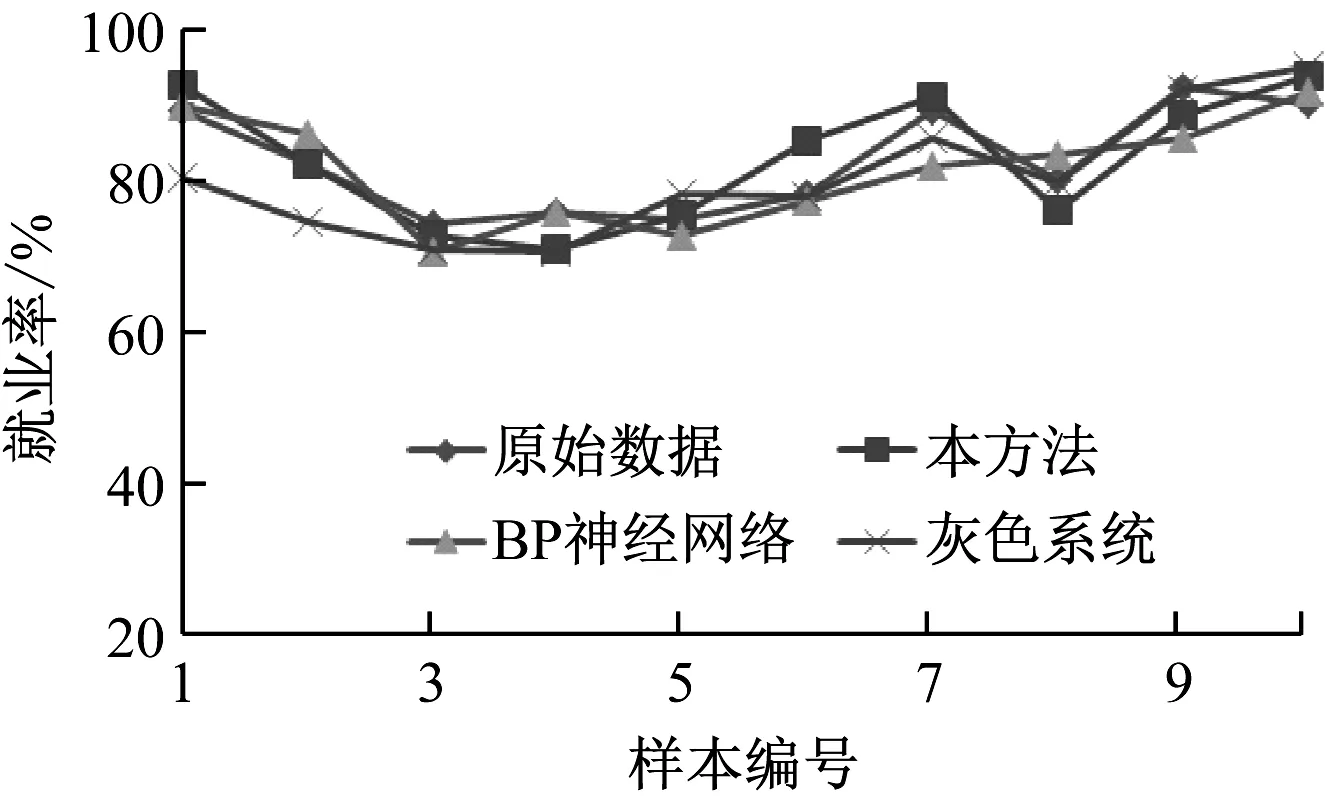
图4 高校毕业生就业率预测结果

对比图3和图4的高校毕业生就业率预测结果如下。

(1) 所有方法的高校毕业生就业率的拟合精度要高于预测精度，这表明它们的拟合能力要优于泛化能力，这符合一般预测方法的建模规则。

(2) 单一模型在预测过程中，无法满足变化规律大、随机性较强的高校毕业生就业率预测，不能全方位反映毕业生就业率变化特点，因此建模效果不够理想。

(3) 相对于BP神经网络和灰色系统预测结果偏差较大的问题，本文方法的预测准确性较高，有效减小误差。组合模型可以充分利用结合模型的优点，对数据进行优化处理，根据就业率变化特点，获取高校毕业生就业率预测结果，有效提高预测精度，由此验证了本文方法的优越性。

2.3 稳定性测试

在全国范围内，随机选择100所高等院校作为研究对象，采集它们毕业生就业率历史数据，并采用不同方法对毕业生就业率进行建模与预测，预测精度如图5所示。

图5 高校毕业生就业率预测结果的稳定性分析

分析图5可知，本文方法的预测精度为96.78%，由于本文方法利用小波分析对数值进行重构，可以有效获取周期内的随机变化特征数值。而BP神经网络和灰色系统预测精度为91.34%和85.97%。由此可见，本文方法的高校毕业生就业率预测精度十分稳定，而对比方法的高校毕业生就业率预测精度波动范围比较大。

3 总结

为了避免当前高校毕业生就业率预测方法存在的弊端，有效减少高校毕业生就业率的预测误差，设计了组合模型的高校毕业生就业率预测方法。具体仿真实验结果表明，本文方法是一种精度高、结果可靠、稳定性高的高校毕业生就业率预测方法，可以为复杂多变的高校毕业生就业率分析提供一种新的方法，有助于分析当代毕业生就业率的实际情况。