基于深度学习的音乐配乐识别研究
2021-11-01赵一鸣
赵一鸣
(榆林学院 艺术学院, 陕西 榆林 719000)
0 引言
大数据时代,随着数据挖掘技术的发展,对海量数据进行挖掘和提炼并转换为有价值信息的技术逐步变得大众化、成熟化[1]。而音乐信息检索和识别也随着数字媒体经济的发展壮大而成为众多学者研究的热门领域,进入20世纪以来,美国的学者Krishna A G率先提出了基于改进的高斯模型和KNN分类相结合算法用于单乐器的音乐配乐识别[2]。来自英国的研究人员Essid S在2012年提出了将梅尔频率倒谱与支持向量机结合的分类算法,用于对多种组合乐器的配乐识别,实验后发现该算法用于K最近邻分类算法,将识别准确率提升到了90%[3]。国内研究人员沈骏针对中国传统乐器的配乐识别提出了基于乐器本身特征增强后的特征识别分类算法,并对经典的KNN算法与卷积神经网络算法进行了结合,该算法可以提高中国传统乐器的配乐识别,但是准确率为92%,对比Essid S提出的算法略有提升,但是算法执行过程中比较耗费资源[4]。基于前人研究的基础上,考虑到深度学习在图像识别领域强大的特征提取能力,本文创新性地探索了深度学习的相关算法在音乐配乐分类识别方面的研究与应用,在经典神经网络的基础上,引入特征值向量,首先对数据集样本进行预处理,结合特征变化参数,强化特征值,然后,基于改进的神经网络算法,建立深度监督学习后的音乐配乐的分类模型,并对测试样本进行模型的应用比对测试,实验证明,改进后算法应用于配乐识别的识别率高达98.4%,明显优于其他经典算法。
1 卷积神经网络CNN
卷积神经网络采用人体神经组织的结构模式,设置卷积层以及为其提供关联的下采样层两层网络关联结构模型[5-6]。其采用一定的规则连接上下两层和相邻的神经组织,建立各个层级中强制的、局部的关联关系,具体如图1所示。
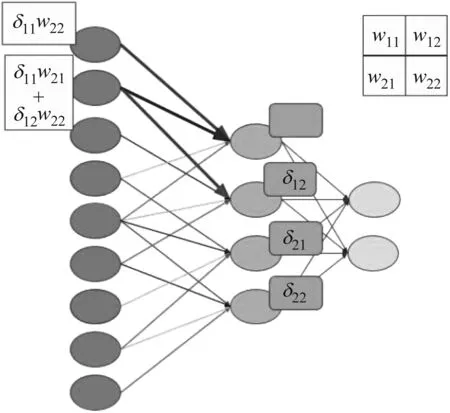
图1 卷积神经网络的网络结构图
由图1可知,每个相邻层级的神经元都强制地互相连接,存在关联关系,该结构在局部空间的输入滤波功能具有强适应性[7]。其主要包括数据输入层和隐含层,每种隐含层细分为卷积层、采样层和池化层。算法的核心是卷积和池化,使用监督学习的模式构建训练网,主要包括前项训练传播和反向训练传播两部分,前向训练传播对输入的训练样本矩阵进行分层变化,每一层的输出即为下一层的输入,最终提取卷积特征矩阵,具体算法如式(1)。
(1)
其中,s(i,j)为特征向量矩阵;输入数据为二维矩阵M×N;wm,n为M×N矩阵的卷积核;wb为偏移向量。在反向训练传播过程中,主要通过采用梯度下降算法,计算损失函数,迭代求出最小误差的极限值,从而达到将训练样本的数据值与计算后的输出值无限接近的目的。其中,常用的损失函数的计算方法如式(2)。
(2)
其中,L代表损失;x代表输入的数据样本;a代表输出结果;y代表标签项值;n代表样本数量。
2 深度置信网络DBN
深度置信网络包括隐藏层和可见层,层间采用全连接模式[8-11],其结构如图2所示。
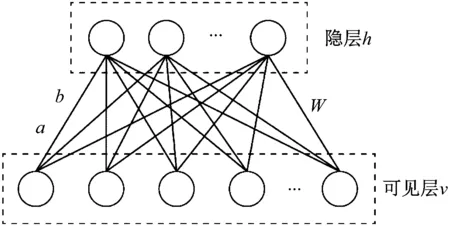
图2 深度置信网络的结构示意图
图中,h代表神经元的向量值;w代表隐藏层与可见层之间的连接权值矩阵。DBN样本模型训练用受限波尔兹曼机构成神经网络感知,其模型如式(3)。
(3)
式中,vi和ci分别代表了第i个显示层和及其对应的显示神经元的偏置;wij代表显示层与隐藏层之间的神经元连接的权重值;hi代表第j个隐藏层;对应的di代表了隐藏层神经元的偏执值。式中的θ={wij,ci,di}。
其中,权重值wij的计算方法为式(4)。
wij=η[Edata(vihj)-Emod(vihj)]
(4)
式中,i和j分别代表可见层节点数量以及隐藏层节点数量;η代表学习的效率值;同时vi和hj代表指二值变量;Edata和Emod代表训练的样本值以及输出样本的期望值。
3 基于CNN&DBN的特征学习算法提取音乐配乐
CNN模型应用于特征提取的优势在于计算复杂度低,特征提取速度快。DBN模型的优势在于克服了神经网络算法中对于数据的要求较高、收敛速度非常慢且局部解决最优全局差的问题,结合两个特征学习算法的优势,本文提出了基于CNN&DBN的特征学习算法提取音乐配乐的特征,完成特征配乐的识别,并经过反复的比对试验、调优,最终达到了识别准确率最高。
具体的执行模拟过程如图3所示。

图3 CNN&DBN的特征学习算法结构示意图
执行的具体步骤如下。
(1) 首先进行输入数据集的预处理,主要是通过音高特征矩阵和常量变化完成噪音过滤和音量校准,预处理后,得到音乐配乐的样本数据集合。
(2) 采用基于CNN模型的改进音乐配乐训练模型,对样本进行监督性学习训练,生成训练特征样本模型。
(3) 引入原始的测试样本集合,也需要对测试集合进行降噪处理。处理后的测试结合,输入CNN提取的特征样本模型。提取新的特征向量。
(4) 将提取的特征向量与原始样本集的分类集合Y组合生成新的输入样本集合,并将样本集合作为输入集合,输入到DBN模型中进行训练,并得出最终的分类训练结果。
本文在新的模型算法的研究过程中,基于音乐配乐多音质结合的复音情况,对CNN模型算法进行了适应性的调整,引入模拟人体的听觉关注点搭建了配乐识别分类基准模型,该模型的关键在于由于人的大脑结构特点决定其在听到音乐时会自动过滤筛选,注意力会关注在音乐的旋律和主声音声部,从而识别出乐器配乐的不同,因此,在本文提出的模型建模的方法中,模拟人脑的操作过程,结合音乐配乐的乐器特点,引入关注度模型后,重点对于不同乐器成分对应的波段设置相对应的特征权重值。具体的模型执行结构如图4所示。
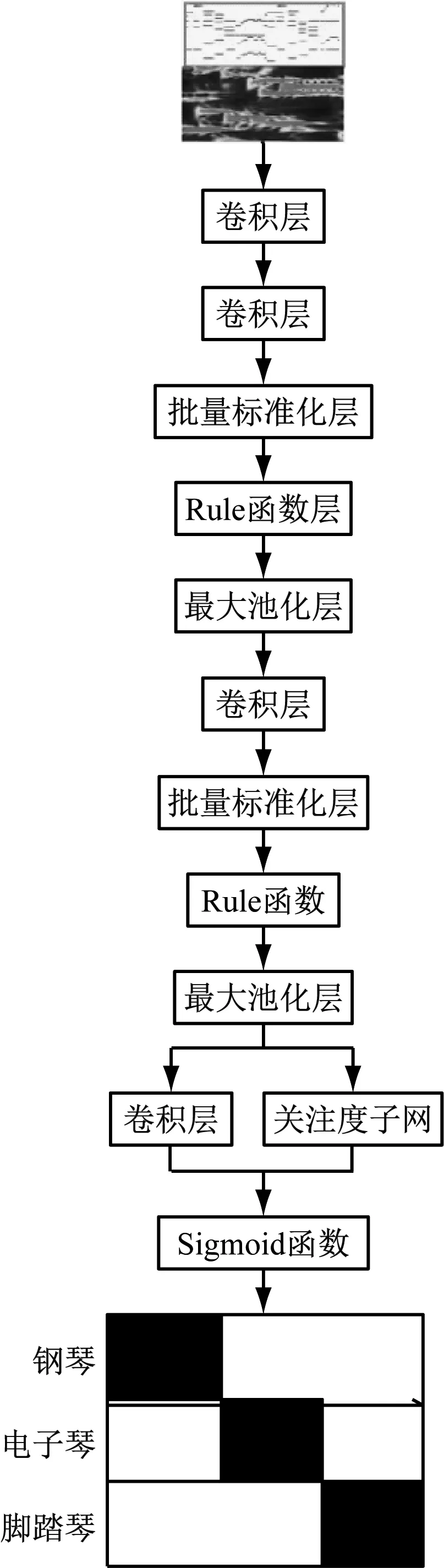
图4 基于关注点网络的配乐识别分类基准BNN模型流程图
如图4所示,基于关注点网络的BNN模型分为卷积层、卷积层、批量标准化层、Rule函数层、最大池化层等。其中,池化层部分引入关注度网络和卷积层,从而生成带有权重值的特征向量,并对特征向量的和使用Sigmoid函数获得识别分类结果。关注度网络包含了卷积层、全连接层和对应的归一化函数,其中特征矩阵卷积后会变成适量矩阵rn,每个适量矩阵输入全连接层会得到关注度适量vn=fall(rn:θall),设置θall作为全连接层的非参数,对全部关注度的矢量的各个分量上使用归一化函数记性标准化,并对M个标准化后的适量求和得an,得出关注度权重值∂n,如式(5)、式(6)。
(5)
(6)
基于关注点网络的BNN模型其流程与传统的神经网络算法类似,核心在于卷积层的关注度因子的引入,该算法中单层卷积的运算次数以及空间占用情况如式(7)、式(8)。
(7)
(8)
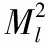
4 实证结果与分析
4.1 训练及测试样本的选择
本文选用的数据样本是以3秒的时长,包含各种乐器的音乐配乐片段,而乐器训练样本上对每种乐器音乐包含3 120个样本,共计21 840个配乐样本。其中乐器选择670个测试样本,共计4 690个测试样本。预处理过程中,首选对样本降噪后,添加标签,使用训练集的模型,测试集与训练集进行交叉测试,同时也验证了对于测试样本配乐的预测能力,最后将预测的配乐标签与实际配乐分类进行比较,最终的准确率为平均计算值的结果。
4.2 结果与分析
结合对传统的分类算法性能的研究,发现深度学习的样本训练过程需要耗费巨大的算力且执行时间较长,常规的实验环境极容易造成实验过程中断和系统宕机的情况,通常需要约为周甚至月为单位进行比对实验,才能到达模型平稳运行的基本状态,同时,还要开展其他算法的对比实验。为了提高性能,本文采用了有限循环法进行实验,限制了执行周期和循环次数,经过反复测算选择了执行9次循环,实验主要对测试本文的CNN&DBN的模型与决策树、最近邻算法KNN、支持向量机SVM进行了准确率比对实验,以及随着循环次数的增加对应执行准确率的变化比照实验,结果发现在循环次数为9时,性能最佳,其结果如表1和图5所示。
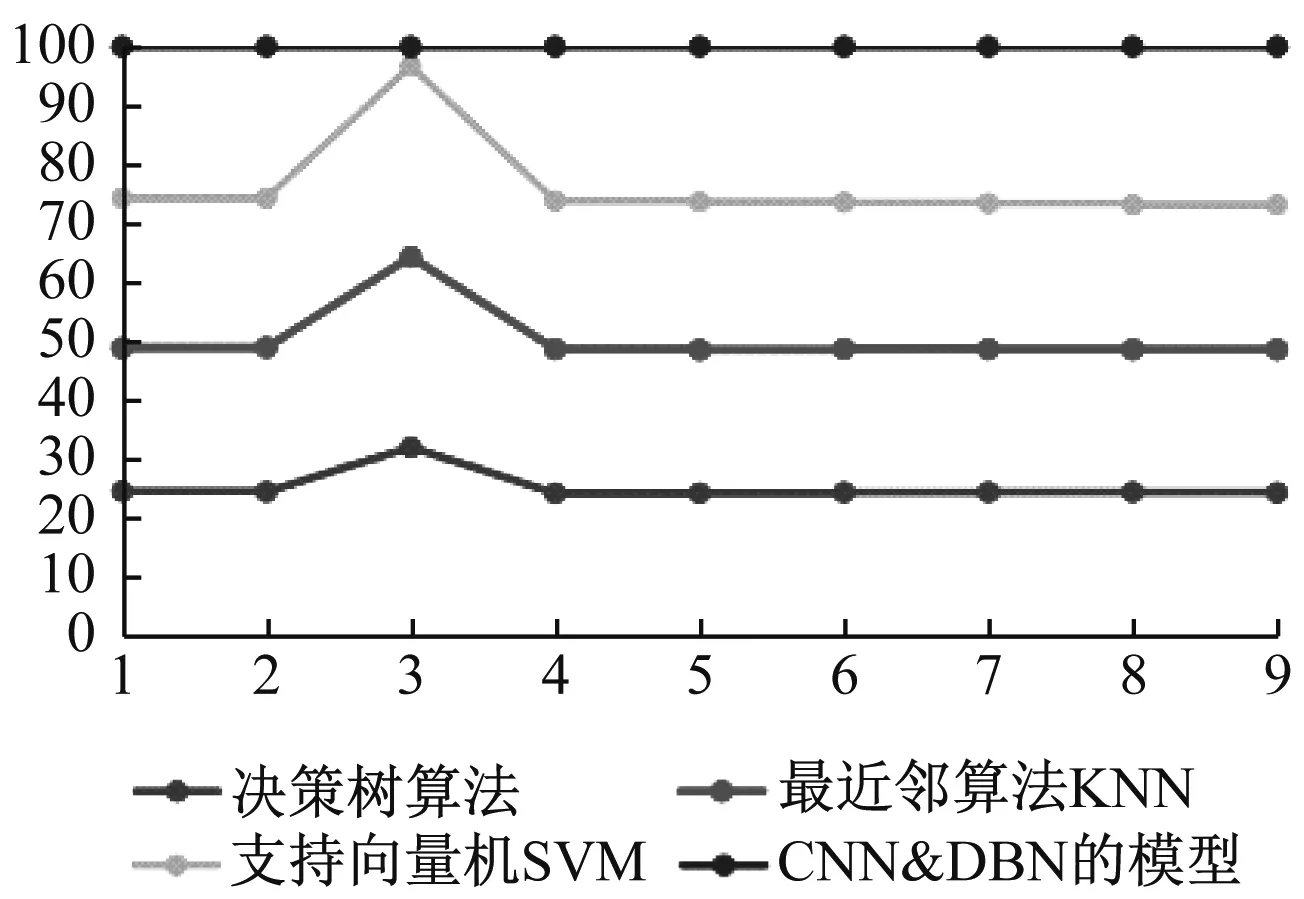
图5 不同循环次数的各个算法准确率对比图

表1 不同算法结果对比
对比其他经典算法识别的平均准确率上,由于本文算法结合了CNN对于特征提取的优势与DBN算法的执行效率高的特点,并在CNN算法中引入了关注度权重,因此,无论是准确性还是性能两方面都有极大的提升,明显高于其他算法。
同时,对比加入关注度权重的CNN模型,其配乐识别精度与其他模型对比如表2所示。
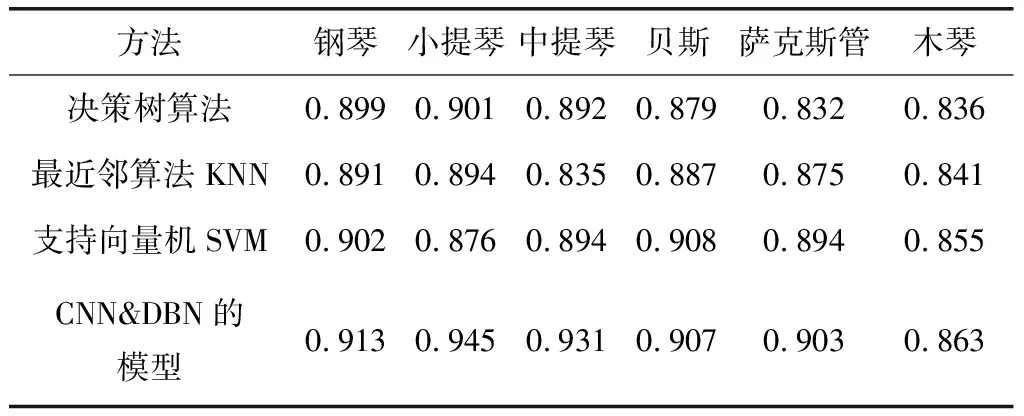
表2 不同算法对于各个配乐识别结果对比
从表2的数据可以得出结论,本文提出的基于CNN&DBN的配乐识别算法,在对各种识别的分数和整体的精度上,对比其他经典模型对于相同数据集的应用识别结果有明显的提升,尤其是对小提琴的识别提升效果更为明显,并且本文的模型对比其他模型,配乐整体识别更均匀,有效地改善了不同类别识别效果不均衡的问题。
5 总结
深度学习与音乐推荐的深度融合在进入智能化、大数据时代逐步成为数据挖掘和机器学习领域研究的热点,本文改进了卷积神经网络(CNN)进行音乐配乐特征向量的识别和提取,并引入深度置信网络(DBN)的执行的高效性,将CNN提取的特征向量集作为DBN的输入集,建立了基于CNN&DBN的特征学习算法提取音乐配乐。经过实验比对发现,本文提出的模型在对多种不同类型的复音配乐的识别能力上,展示出了更精准的识别能力和良好的执行性能,改进后算法应用于配乐识别的识别率高达98.4%,明显优于其他经典算法,实验数据充分说明了本文算法在对音乐配乐识别方面的明显优势。
