基于统一谐波模型的双有源全桥变换器功率计算

杨 挺， 李 艳， 王 雄， 蒋晓雁

（榆林学院能源工程学院，陕西榆林 719000）

0 引 言

双向双有源全桥（Dual Active Bridge，DAB）具有在零电压开关下对宽输入范围电压进行升压和降压的能力，这使其可适用于许多应用［1-9］。在双有源全桥中计算输出功率或输出电流的传统方法是求解每个间隔中的电感器电流方程，以获得持续时间和电感器电流值［10-12］。如文献［1］中所提到的，当同时控制两个桥的脉冲宽度调制（PWM）和相移时，则存在10 种不同的电路运行模式。而要计算每个运行模式中的功率，这个过程就会既耗时又费力［13-14］。

本文介绍一种基于傅里叶变换分解项代数和的新方法。该方法不需要确定电路运行模式及其持续时间，将电路的暂态关系进行傅里叶分解，再对分解项进行累加求和，以解决暂态数据的不确定性问题。该方法可以降低对系统状态的依赖性，并简化计算。通过仿真分析证明了理论的正确性。

1 系统结构及原理

双有源全桥的电路如图1 所示。基于开关信号，变压器两端的电压表示为级数的形式：

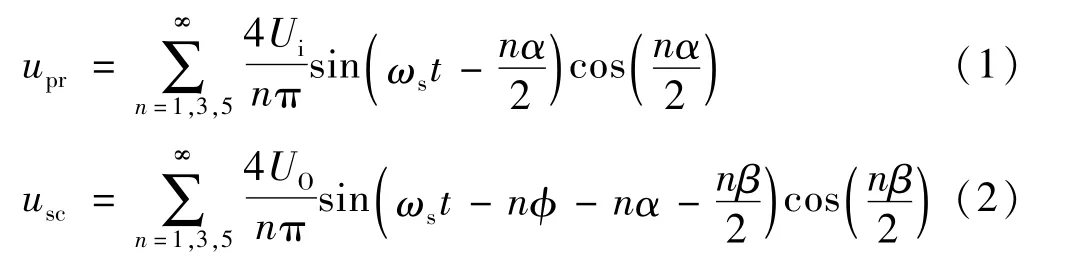
式中：upr、usc分别为变压器输入、输出电压；Ui、Uo分别为电源与负载端电压；α、β、φ 分别为开关S3、S5的触发角以及S6与S1的触发角之差（见图1）；n为傅里叶变换的第n项；ωs为电压角频率。

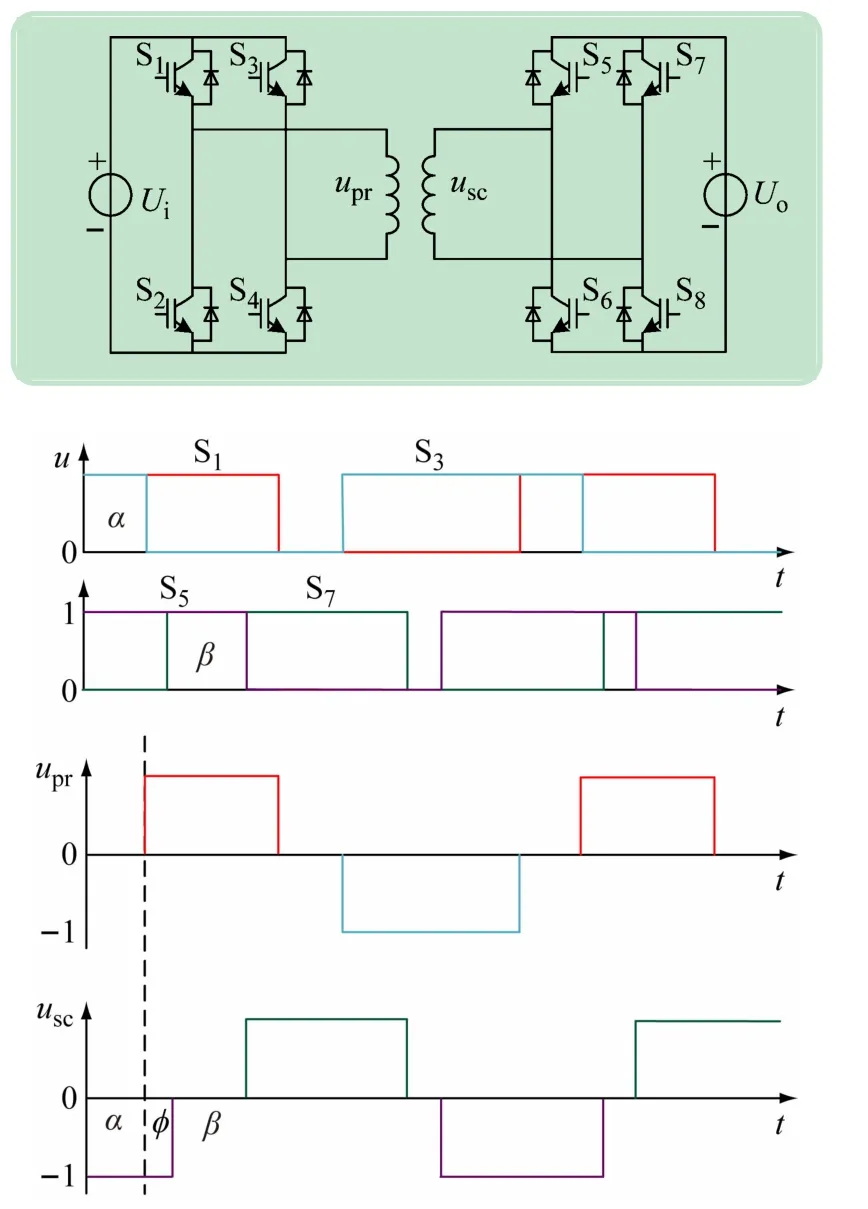
图1 双有源电桥的电路图及开关信号

基于文献［5］中的功率流动可以将功率表达式写成：

式中：L 为双有源全桥电路的等效电感值；fs为时域频率。

在限定范围内的奇数周期函数的级数展开可简化为：

对应于式（5）的级数可以通过在傅里叶级数展开中加入t ＝0 来写成如下形式：

由于式（5）、（6）表示相同的函数，因此由以下等式成立：

初级和次级之间的相移是

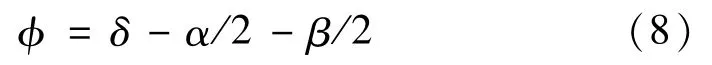
式中，δ 为信号的初始相移。将式（8）的值代入式（4），可得：

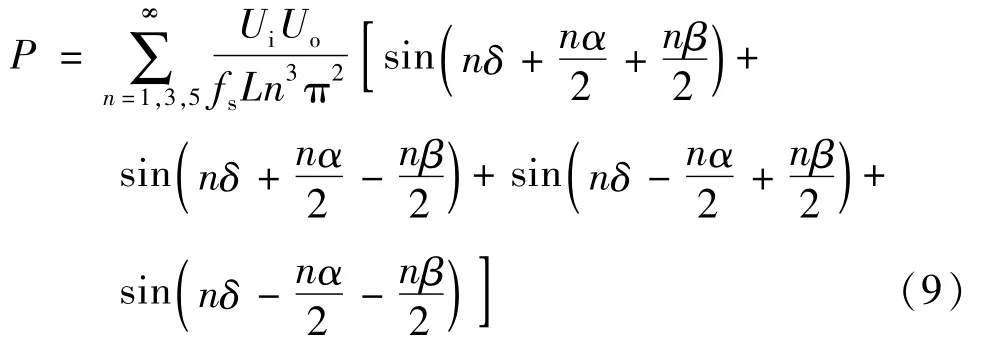
对比式（9）、（7）并且将其归一化，可以得到如下结果：

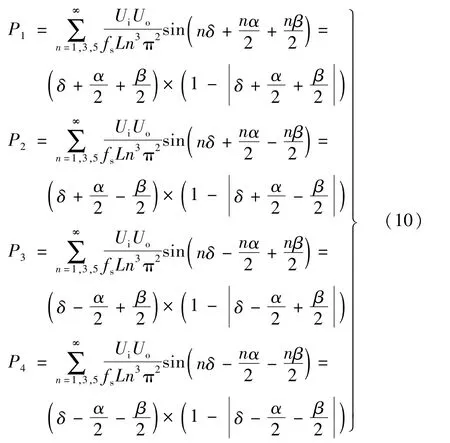
基于表达式（10）来看，总共有4 种运行模式，但是从P1的正弦表达式来看其存在超出π 的部分。因此，这部分用式（10）表示P1就不再准确，－ π ＜x ＜π时P1的正弦表达式则由式（11）来表示：

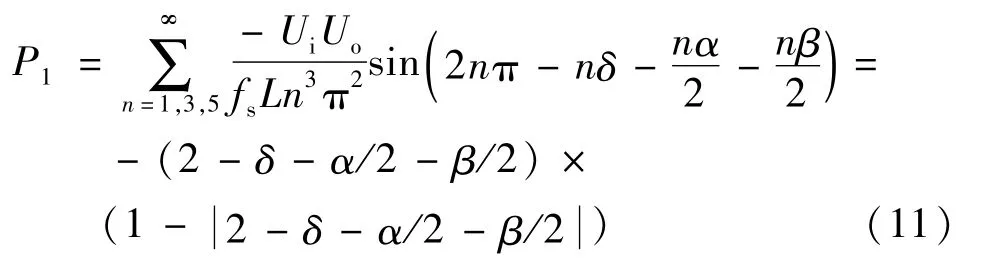
因此总的运行模式增加了一个达到5 个。模式IA见表1。

表1 模式IA δ≥（α/2）＋（β/2），α ＋β ＞π

情况IB 具有与情况IA 相同的条件，但式（9）中右边方程第1 个正弦项现在位于－ π ＜x ＜π 的范围内。因此，如表2 所示，可以由式（10）所示计算功率。模式II和III 是当式（9）的第2 或第3 项中的任何一个变为零。此时合成功率将根据表3 和4 计算。

表2 模式IB δ≥（α/2）＋（β/2），α ＋β ＜π

表3 模式II δ ＜（α/2）－（β/2），α ＞β

表4 模式III δ ＜（β/2）－（α/2），β ＞α

模式IV 是在模式I ～III 之间发生相移的情况。下限由模式II或III得到，而上限由模式I给出，因此，4 种运行模式下的功率表达式见表5。

表5 模式IV ｜（β/2）－（α/2）｜＜δ ＜min｛［（β/2）－（α/2）］，（π－（α/2）－（β/2））｝

每种模式下的功率计算可写为：

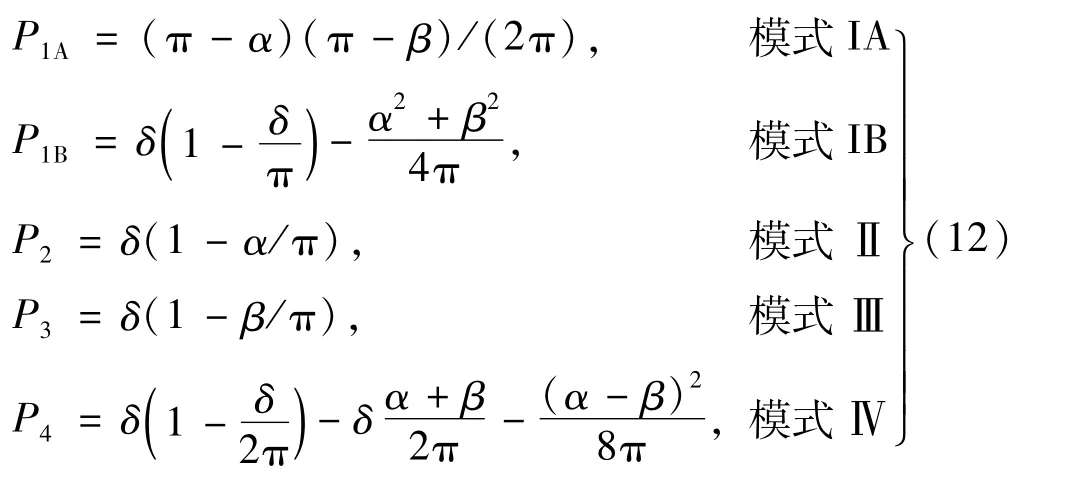
该方法可以扩展到单个PWM 和相移调节。对于初级侧PWM，α将变化，β将为零。而对此次级侧调制PWM正好相反，β将变化，α将为零

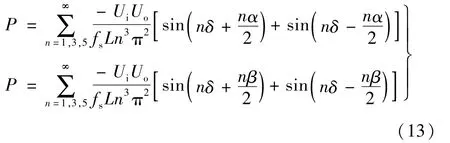
使用式（7）并遵循与双PWM相同的过程，可以将式（13）内容写成

由（14）可见，在单个PWM 中有3 种可能的运行模式。次级侧调制的功率流方程将与（14）相同。α将被替换为β。表6 显示了3 种不同的情况及其计算结果。

基于表6 中3 种不同情况下的功率流可以写成：

表6 单PWM调制

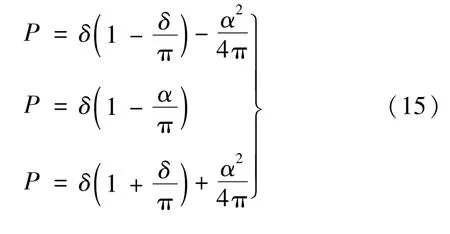
2 仿真分析

使用Matlab 进行仿真，如图2 所示为仿真与计算对比图，结果显而易见。如图1 所示结构搭建平台，直流输入电压Ui＝30 V，系统频率f ＝19.5 kHz。图3 为upr与usc的实验波形。

图2 仿真值与计算值对比

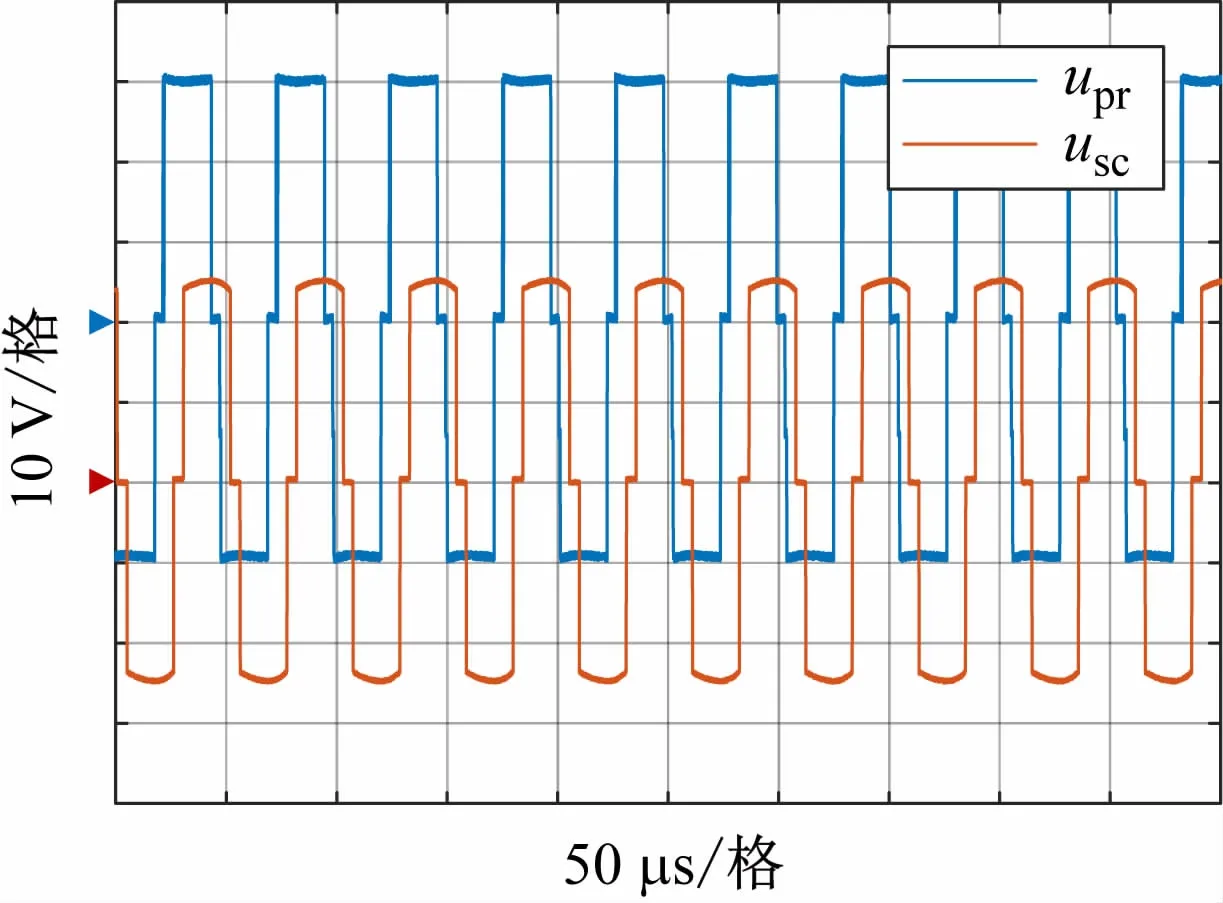
图3 upr与usc的实验波形

图4所示为选取了5 组实验测得数据与理论计算值的对比，可以看出两者存在一些偏差。这是因为实验器件存在相应的损耗，而在理论推导中忽略了这些因素，同时测量过程也可能存在一些误差，因此，得到此结果是可以接受的。

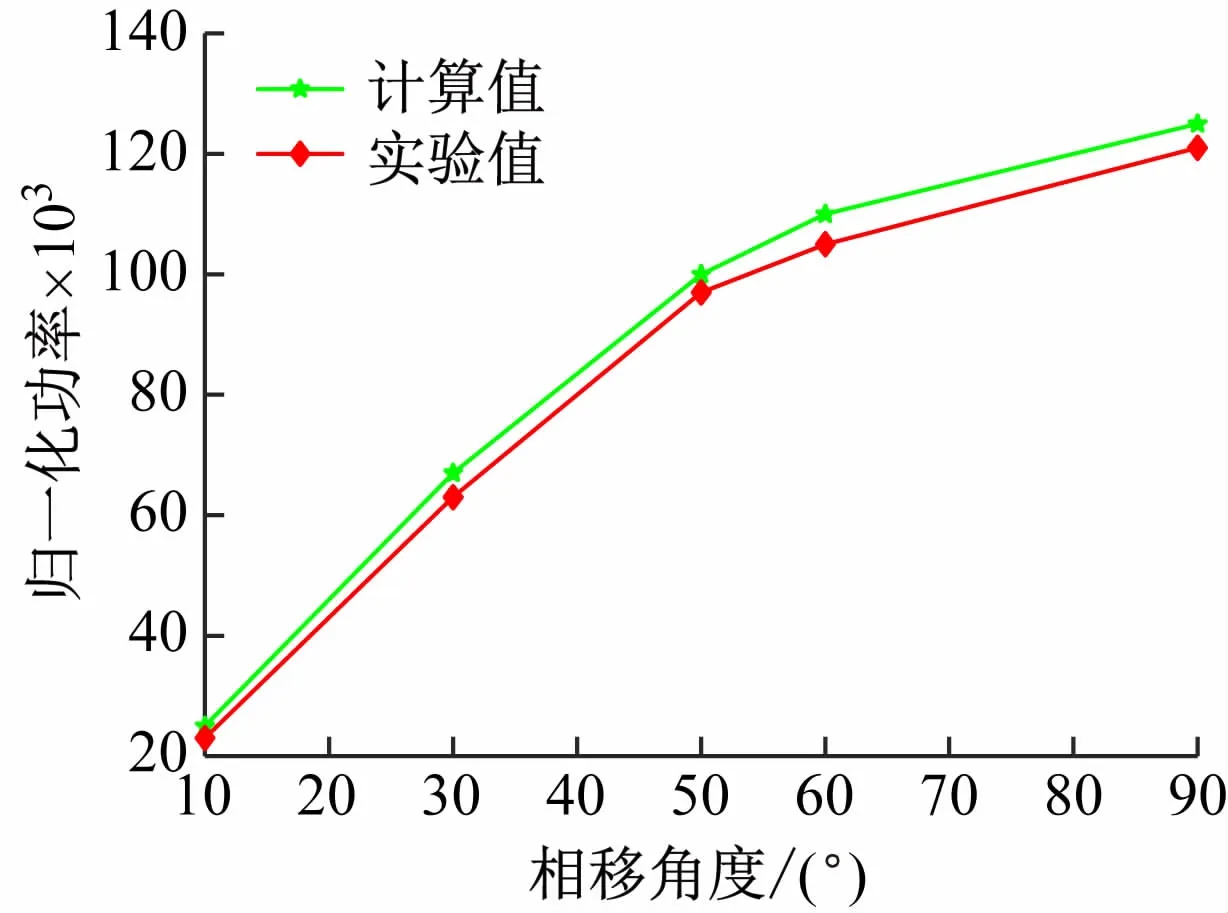
图4 实验值与计算值对比

3 结 语

本文提出了一种新的基于统一谐波的双有源电桥功率计算。在传统方法中，为在不同情况下计算功率，需要计算电流值和持续时间。该方法很麻烦，并且其复杂性随着控制参数变量的增多而增加。本文提出了一种新颖的基于傅立叶的统一谐波分析方法，以减少功率计算的复杂性和时间。最后，通过仿真和实验验证了理论的正确性。