基于低相干光干涉的相位成像实验系统

刘 扬， 王 毅， 周红仙

（东北大学秦皇岛分校a.实验教育中心；b.控制工程学院，河北秦皇岛 066004）

0 引 言

光学干涉是一项重要的精密检测技术，具有非接触、灵敏度高等优点［1-2］。利用光学干涉中的相位变化可以实现纳米及亚纳米精度的检测，但是，由于存在相位卷绕问题，其测量范围受到限制。相位卷绕是光学干涉技术的固有问题，由于干涉耦合项为余弦函数，其周期性导致无法解调出真实相位，只能给出位于［－ π，π］的主值部分（即卷绕相位），卷绕相位与真实相位之间相差2π的整数倍［3-6］。

有效的相位解卷绕能扩大干涉测量范围，目前，已有多种相位解卷绕方法被提出，最常用的是数值解卷绕方法，它是根据相位的连续性，当相邻点相位差较大时，即认为是产生相位卷绕，进行相应的相位补偿，但是当样品相位变化较大或噪声较大时，数值解卷绕会出现错误，而且，当相邻两点的相位差大于π 时，理论上数值解卷绕就无法恢复真实相位［7-8］。

相位［－ π，π］对应光程范围为［－ λ/2，λ/2］，λ为探测光波长，为了避免相位卷绕，可以增加探测光的波长，但是探测光波长增加是有限的。Forrester等［9-10］提出了合成波长方法，采用双波长相位解调解决光源波长较小的问题，利用两个波长的相位差，形成比单一波长更大的等效波长λS（合成波长），合成波长可达到微米甚至毫米范围，使相位可测量的范围扩大。但是，当光程超过出这个范围时，仍然会产生相位卷绕，而且合成波长方法会放大噪声。

近几年，在白光干涉技术中，多种相位解卷绕的方法被提出，例如Yan 等［11-12］提出了定量相位成像技术，首先利用线性回归计算出一个分辨率较低的结果，然后以此结果为对照，进行相位解卷绕。本文提出了一种基于干涉光谱逼近的方法［13］进行相位解卷绕。和数值解卷绕方法不同，这些方法理论上不受相邻两点相位差小于π的限制，可以在较大范围内实现高分辨率成像。

1 实验装置和方法

1.1 实验装置

图1 为实验系统示意图，光源为超辐射发光二极管（VSLS-840-B，Connet LASER），中心波长840 nm，带宽40 nm。从光源发出的光通过一个光纤环形器，从环形器端口输出的光经准直器变为平行光，用分束器将平行光分为参考光和样品光。参考光被聚焦到一个平面反射镜；样品光经过XY 扫描系统后，被一消色差透镜聚焦在样品表面。被样品和参考臂反射镜反射的样品光和参考光返回到环形器，然后进入到自制的光谱仪中。光谱仪主要由透射光栅（1 800 线/mm，Wasatch Photonics）和线阵相机（raL2048-80 km，Basler）组成［14］。

图1 实验系统示意图

1.2 实验方法

图1所示实验系统中，当样品只有一个反射面时，干涉光谱可表示为［15］

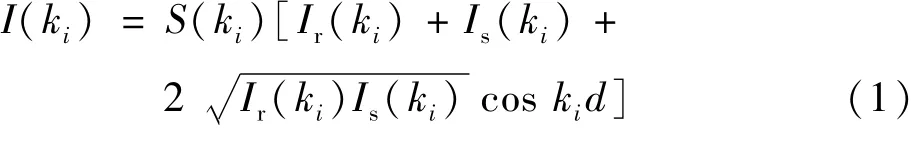
式中：ki表示光谱仪第i 个像素对应的波数；S（ki）为光源强度分布函数；Is和Ir为样品臂和参考臂的反射光光强；d是待测光程。假定其对应的相位为

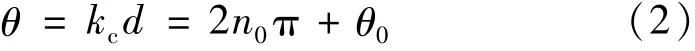
式中：θ0为位于［－ π，π］的主值相位（卷绕相位）；kc为光谱仪的中心波数。对式（1）进行快速傅里叶变换（FFT）只能得到θ0，无法确定n0，因此θ 和d 无法确定。

数值解卷绕过程如下：逐点判断θ0相邻两点光程差，如果相位差小于π，补偿2π；如果相位差大于π，补偿－ 2π。

合成波长相位解卷绕步骤如下：把干涉光谱I（ki）均分成两部分，假定两部分子光谱的中心波长分别为λc1和λc2。对这两部分干涉光谱分别进行FFT，得到两部分光谱的相位θ1和θ2，计算两者的差

式中，λS为合成波长，λS远大于单一波长λc1及λc2，因此使用合成波长可以在一个较大的范围内不发生卷绕。本实验系统的合成波长为42.373 μm。

式（1）中光程d可表示为

式中：m0为整数；Δd为FFT的频率分辨率，Δd等于2π/Δk，Δk为光谱仪波数宽度，为光谱仪已知参数；θ0为卷绕相位；n0为待求整数。对干涉光谱进行FFT 得到θ0和m0。基于干涉光谱逼近的相位解卷绕步骤如下［7］：

①构造仿真干涉条纹

②将测量的干涉光谱I（ki）和每个仿真干涉光谱I′（ki；n）分为两个子光谱，k′c1和k′c2分别表示两个子光谱的中心波数。

③对每个子光谱进行FFT 计算出每个子光谱的卷绕相位，令θ1和θ2表示测量的干涉光谱的结果，θ′1（n）和θ′2（n）表示仿真干涉光谱的结果。

④计算函数

假定φ（n）达到最小值时，n ＝nmin，则得到未知整数n0＝nmin。

2 实验结果及讨论

2.1 实验结果

首先，对倾斜的USAF1951 分辨率板的表面轮廓进行相位成像，通过蒸镀铬在分辨率板表面形成不同宽度的条纹，条纹高度约为100 μm。为了降低外界干扰，采用共光路方式，将一个载波片置于分辨率板上，间距约为1 mm，载波片下表面反射光为参考光。分辨率板表面轮廓的成像结果如图2 所示，图2（a）为使用FFT计算的相位图，由于相位卷绕，形成了沿X方向的跳变；使用数值去卷绕的结果如图2（b）所示，由于分辨率板表面高度变化较小，因此使用数值解卷绕可以正确进行相位成像。使用合成波长方法的结果如图2（c）所示，由于本试验系统的合成波长为42.373 μm，因此在样品整个高度范围内，没有产生数相位卷绕，但是噪声明显变大。使用干涉光谱逼近法的结果如图2（d）所示，可以高分辨率的解调出样品的表面轮廓。

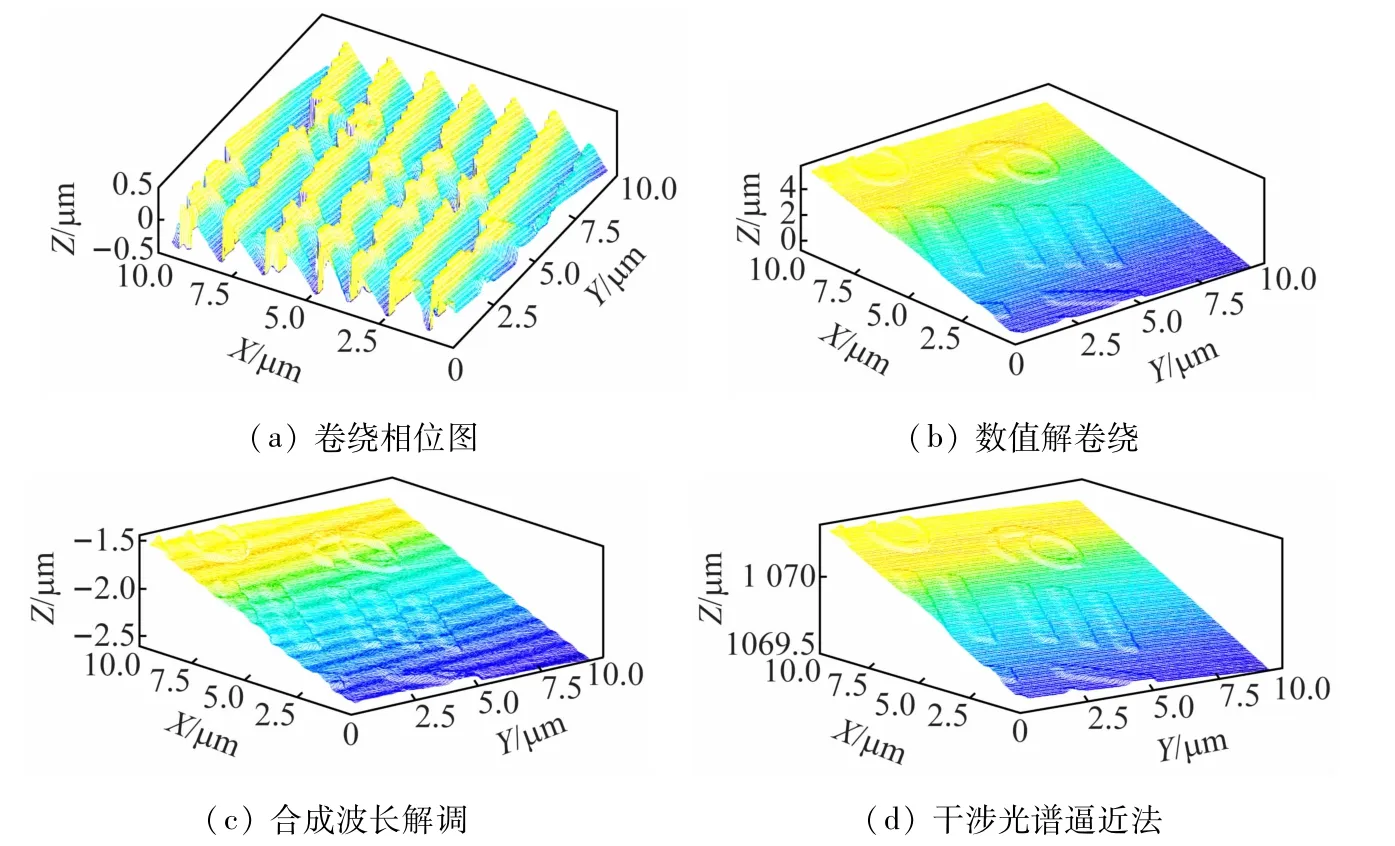
图2 分辨率板的相位成像结果

为了比较这3 种相位计算方法在较大高度范围的差异，对高度为300 μm的阶差规进行线轮廓成像，沿着高度差方向进行一维扫描（见图3（a）中红线），同时，采用如图1 所示的非共光路方式，增大外界干扰。阶差规的线轮廓成像结果见图3（b）、（c）和（d）。图3（b）为干涉光谱逼近方法测得阶差高度为299.98 μm；图3（c）、（d）分别为数值解卷绕和合成波长方法解调曲线。

图3 阶差规的线轮廓成像结果

2.2 讨 论

在图2 所示倾斜的分辨率板表面轮廓成像中，由于样品表面轮廓高度范围只有几个μm，而且使用共光路方式，外界干扰较小，因此数值解卷绕可以正确解调卷绕相位，得到正确的表面轮廓分布；对于合成波长方法，由于高度范围小于合成波长，根据式（3）可以得到表面轮廓（d ＝θSλS/4π），和图2（b）相比，图2（c）的噪声明显增大。比较图2（b）和（c）可以看出，使用干涉光谱逼近方法和数值解卷绕都具有较小的噪声。

对于本实验系统，光源的中心波长和合成波长分别是0.84 和42.373 μm，中心波长和合成波长远小于阶差规高度（300 μm），因此使用数值解卷绕及合成波长方法都无法正确计算阶差高度，如图3（c）和（d）所示。对于阶差规的两个平台面，由于采用非共光路方式，外界干扰较大，因此导致数值解卷绕在两个平台面依然计算错误。对于合成波长方法，由于在两个平台面上没有产生卷绕，因此仅仅在平台面可以正确解调。

对于分辨率板和阶差规，干涉光谱逼近方法都给出了高精度解调结果，说明干涉光谱逼近方法优于数值解卷绕和合成波长方法。如式（4）所示，d ＝m0Δd ＋θ/kc，干涉光谱逼近方法结合了FFT的频率和相位，频率决定测量范围，相位决定测量精度。把光程d 分成两部分，用m0Δd 表示较大的部分，用θ/kc表示小于Δd的部分。在本系统中，Δd等于10.6 μm，因此把解卷绕限定在一个较小的范围。干涉光谱逼近方法的理论测量范围等于4π/（Δk/N），Δk 表示光谱仪的波数宽度，N表示光谱仪的采样点数，Δk/N 表示光谱仪的波数采样间隔。对于本系统，理论测量范围大概是10 mm。干涉光谱逼近方法计算复杂，如式（5）和（6）所示，需要使用多次迭代，计算速度较慢，不适合于实时处理系统。

3 结 语

基于相位检测的光学干涉技术可以达到纳米及亚纳米的测量精度，是一种重要的精密检测技术，而相位卷绕是干涉技术的固有属性。本文建立了一种基于低相干光干涉的相位成像实验系统，用该实验系统对分辨率板和阶差规进行了表面轮廓成像，对数值解卷绕、合成波长法及干涉光谱逼近方法进行了比较说明，该实验系统有助于学生了解掌握光学干涉中的相位计算方法及存在的问题。