层间冷却对多道焊厚板残余应力及变形的影响

宁 佶

（三江学院机械与电气工程学院，南京 210028）

0 引 言

焊接过程中，由于焊缝附近材料不均匀的收缩和膨胀，残余应力和变形的产生是不可避免的［1］。焊接变形和残余应力不仅影响结构的外观，而且改变结构的连续性和完整性，从而对焊接结构的屈曲强度等力学性能造成影响［2］。因此，从焊接变形控制与焊接结构强度设计角度来讲，必须从焊接机理出发，对焊接过程与焊后残余应力与变形进行分析。

作为一种常见焊接结构，厚板焊接结构广泛应用于建筑、造船、锅炉压力容器灯光工业部门。对于厚板的焊接一般采用电渣焊、多层多道焊［3-6］（手工电弧焊、埋弧焊、窄间隙埋弧焊、TIG 焊和MIG 焊等）以及电子束焊。由于设备等方面的原因，大多数工厂均采用多层多道焊。张琪［7］对船用D36 钢多层多道焊角变形规律进行了数值模拟；朱忠尹［8］对大型构件多层多道焊焊接变形进行了数值模拟；李慧娟等［9］利用ANSYS软件中的单元“生死”技术对厚板多层多道焊焊接过程进行了模拟；孙永宾等［10］基于Marc 对多层多道焊进行了数值仿真研究；严仁军等［11］对100 mm特厚板多层多道焊的残余应力进行了对比分析研究。

焊接引起的结构变形受设计因素和制造因素的影响。重要的设计因素包括材料热力学性能，如板厚，结构形式，焊接接头类型和细节影响；制造因素包括焊接方法、热输入、焊接速度和顺序，连接策略和力学边界条件［12］。本文基于热-弹塑性有限元，使用MSC.Marc软件，对一厚板的多层多道焊过程进行数值模拟，研究层间冷却时间对焊接残余应力及变形的影响。

1 热弹-塑性有限元法

考虑到焊接过程中温度场对力学响应几乎没有影响的事实，本文使用顺序耦合热弹-塑性有限元法：首先是热传导分析，产生焊接过程的瞬时温度场，然后将温度结果作为外载荷应用到力学模型上。材料不均匀的热膨胀和收缩会产生结构的应力、塑性应变和变形响应。

热分析中，瞬时非线性热传导分析的有限元公式是基于下式中的控制方程和边界条件［13］：

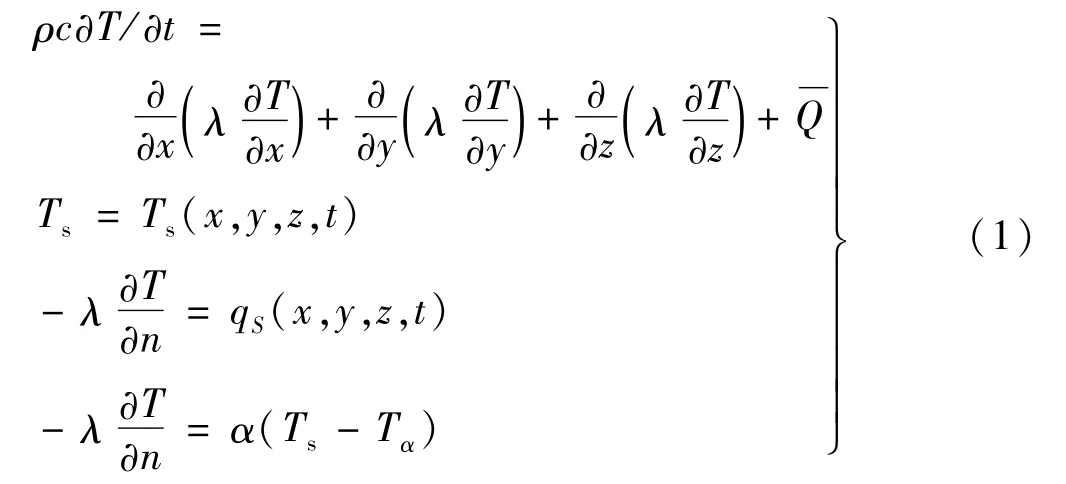
式中：ρ、c、λ分别是材料密度，比热容和热传导系数；T为瞬时温度；Q是内部热产生速率，W/mm3；Ts是环境温度；α是对流系数。

在力学分析中，总位移增量可以表达为下式中各部分的和［12］：

式中：dεtl代表总应变增量；dεe、dεp、dεth、dεpt、dεc分别代表弹性、塑性、热、蠕变和相变诱发应变。

弹性应力-应变关系遵循各向同性胡克定律，并使用凡-米塞斯准则和线性各向同性硬化准则来确定塑性行为。热应变可以考虑使用热膨胀系数。因为在焊接过程中热循环是短暂的，蠕变被认为对总应变的贡献不大，可以被忽略。由于同样的原因，本文的工作中也忽略了相变引起的应变。在力学分析中考虑了几何非线性大变形。

2 有限元模型

2.1 几何模型

研究对象的模型形状如图1 所示，模板为平板，尺寸为900 mm × 400 mm × 25 mm，采用4 层10 道焊。定义L1和L2为模型上的两条路径，计算结束后输出这两个位置的等效应力与位移。

图1 材料的几何模型（mm）

2.2 有限元模型

使用MSC.Marc 软件进行厚板结构建模，单元类型为C3D8R（8 节点缩减积分沙漏控制线性单元），模型的节点数为4 161，单元数为3 078。整个模型的网格划分如图2 所示。

图2 材料的有限元模型

目前，奥氏体不锈钢是应用最为广泛的不锈钢，占不锈钢产品的70% ～80%［14］。分析中使用41Cr4 奥氏体钢，其材料属性是温度相关的，如图3 所示。这些属性包括热传导系数、比热容、热膨胀系数、弹性模量和屈服强度，它们将会影响热学和力学仿真结果。为防止多层多道焊发生较大角变形及挠曲变形，实际焊接过程中采用四角固定的方式，如图2 所示。模型中不考虑重力载荷。

图3 材料的属性

2.3 热 源

焊接热源模型主要有面热源、线热源、体积热源、组合热源、双椭球热源等［15］。董志波等［13，16］认为，利用双椭球热源模型更接近实际焊接情况，因此本文使用宽度5 mm，深度5 mm，前端长度4 mm，后端长度8 mm的双椭球热源模型进行焊接。

由于平板对接多层多道焊需要进行多次直线焊接，所以焊接路径需要定义多次，并且皆为直线。焊接路径的定义通过首末端点来定义。焊接路径定义结果如图4 所示。焊接路径上的各个箭头的意义分别为：红色箭头为焊料表面熔池半径方向；绿色箭头为熔池深度方向，即为焊丝下料方向；蓝色箭头为焊接熔池前进的方向。

图4 焊接路径定义结果

3 结果与讨论

为了研究层间冷却对多层多道焊厚板残余应力及变形的影响，设计了两种不同的工况，①工况1，层间不冷却，一道焊缝填充完毕后，立即进行下一道焊缝的填充；②工况2，层间冷却200 s，一道焊缝填充完毕后，自然环境下冷却200 s，再进行下一道焊缝的填充。

3.1 焊接引起的变形

经计算，两种工况下厚板的最终变形分别如图5、6 所示。图中凸起部分为焊缝高度，为了便于观察，变形放大3 倍。

图5 层间不冷却时厚板的最终变形

两种工况下L1位置的最终变形如图7 所示。可见，在多层多道焊作用下，厚板中心线向焊丝下料方向收缩，使得整个模型发生角变形，这与客观事实是相符的。

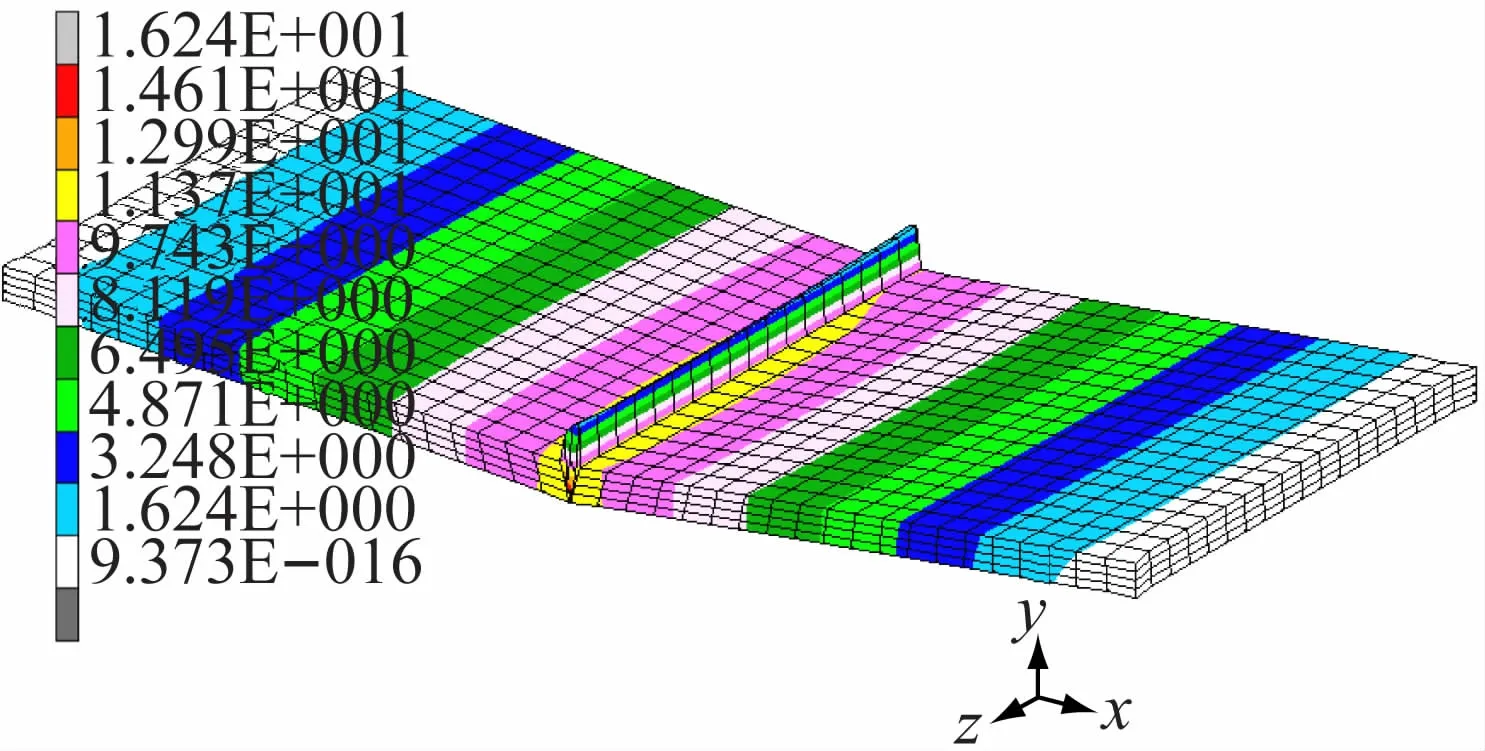
图6 层间冷却200 s时厚板的最终变形

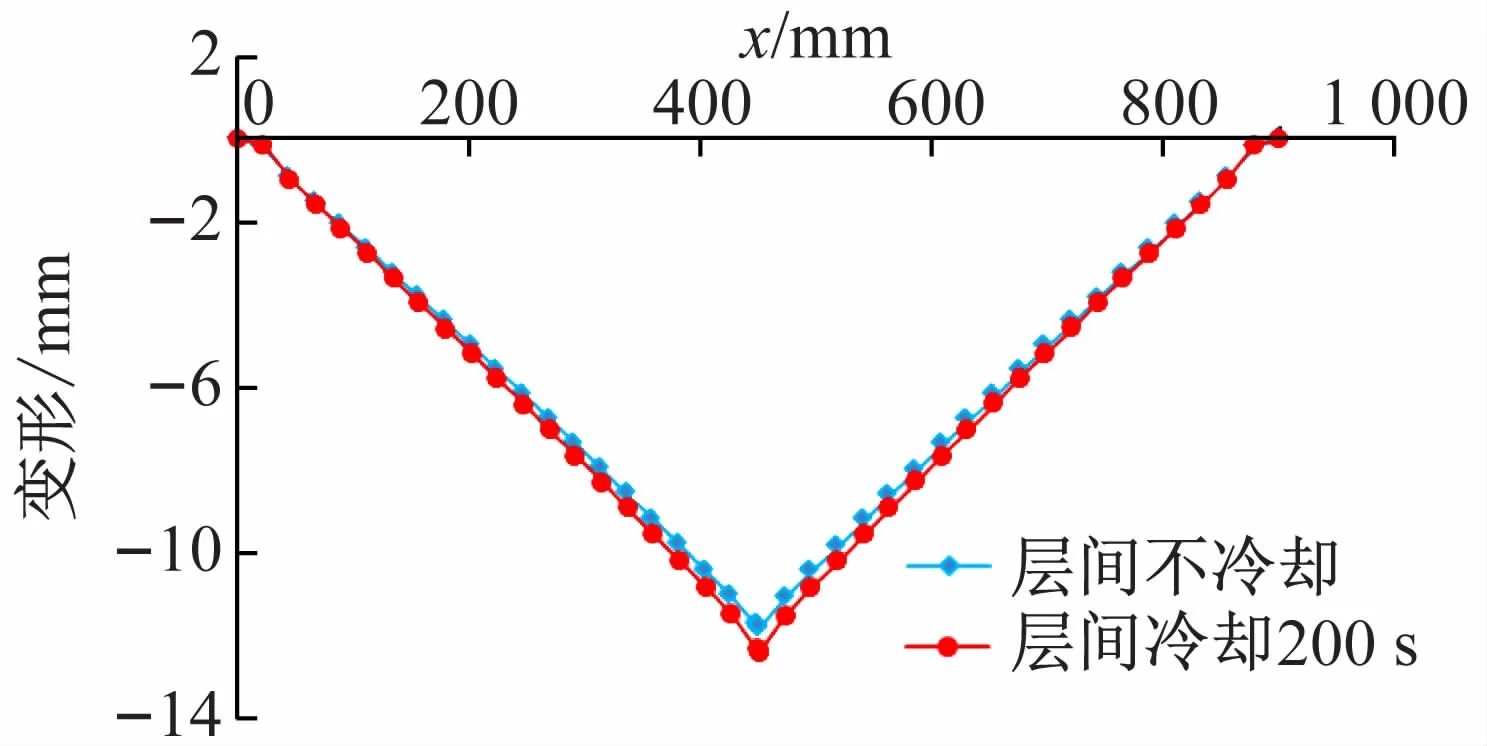
图7 两种工况下L1 位置的最终变形

两种工况下角变形最大值均出现在焊缝区域，变形方向为y轴负向。层间不冷却时，最大变形为14.57mm（0.58 倍板厚）；层间冷却200 s 时，最大变形为16.24 mm（0.65 倍板厚）。可见，在进行厚板多层多道焊时，层间冷却比层间不冷却造成的变形略大。

3.2 两种工况下厚板的残余应力

两种工况下厚板的残余应力分别如图8、9 所示。两种工况下L1位置的等效应力如图10 所示。由图可知，层间不冷却时，厚板最大残余应力出现在焊缝区域，为压应力，大小为274.1 MPa（0.35 倍材料屈服强度）；而层间冷却时，焊缝中心的压应力几乎消失，这是由于冷却过程中，材料收缩，从而将压应力抵消，焊缝附近仍然表现出较大的压应力，约为0.15 倍屈服强度，但相对于层间不冷却，冷却过程有望使多层多道焊厚板焊缝附近的残余应力减小约57%。层间冷却200 s时，整个厚板残余应力的最大值出现在模型的四角，大小为267.1 MPa（0.34 倍屈服强度）。

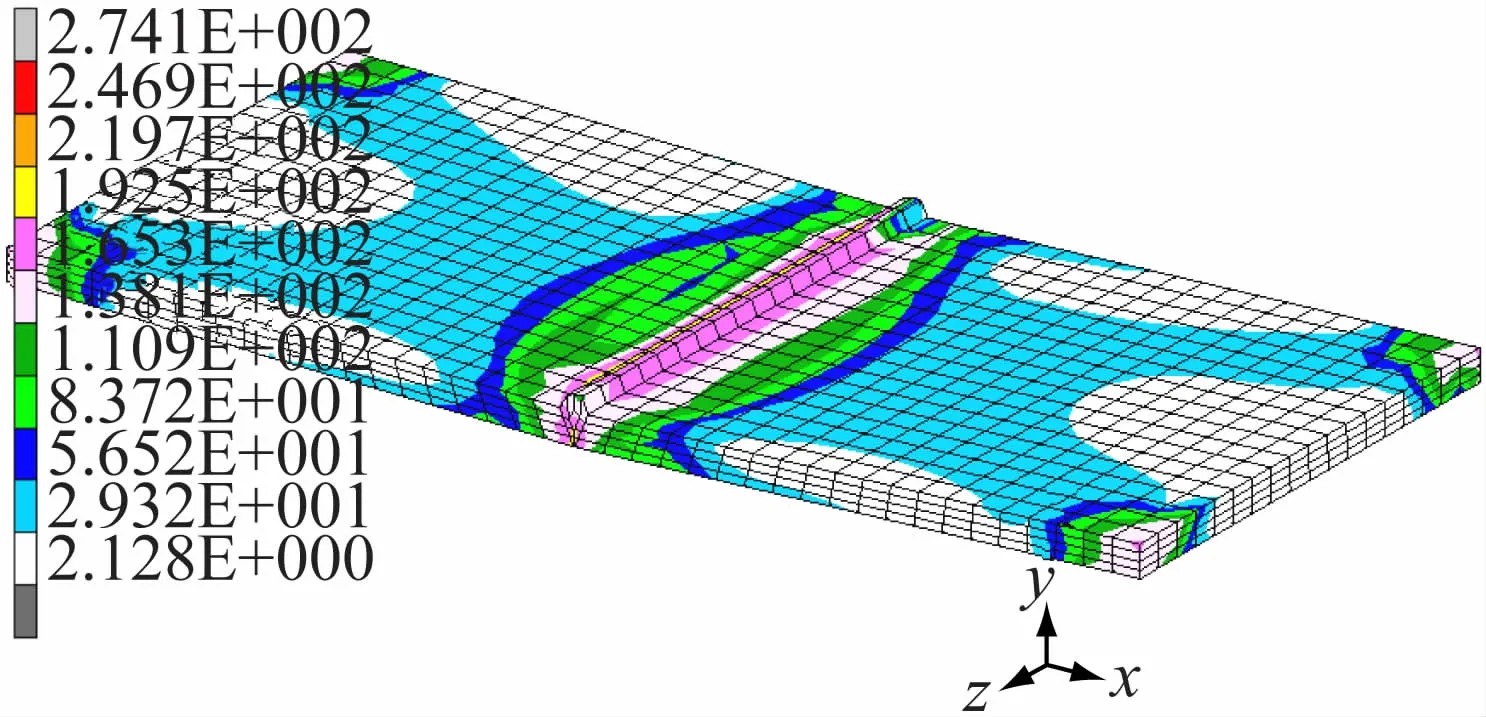
图8 层间不冷却时厚板的残余应力云图

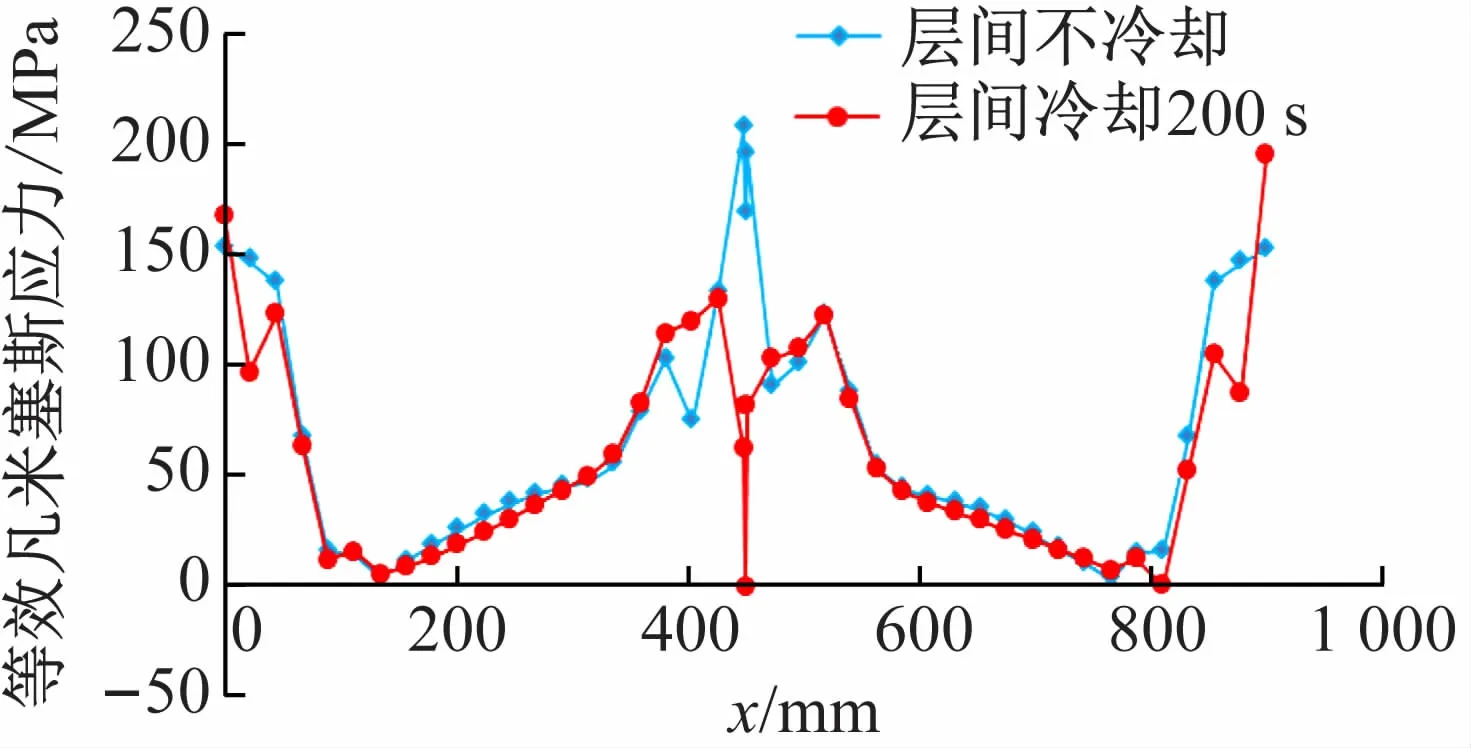
图10 两种工况下L1 位置的残余应力

两种工况下L2位置的等效应力沿板长方向的变化如图11 所示。由图可知，两种工况下L2位置的残余应力分布相似，残余应力沿板长方向逐渐增大，到板中心（焊缝位置）时达到最大，可见层间冷却对L2位置的焊接残余应力几乎没有影响。

图9 层间冷却200 s时厚板的残余应力云图

图11 两种工况下L2 位置的残余应力

对比图10 和11 可以发现，多层多道焊厚板的残余应力沿板宽方向有明显的变化：在模型四角，残余应力较大，甚至有可能成为整个模型残余应力的峰值；而在板宽边的中心，残余应力迅速减小为0。可见力学边界条件对多层多道焊厚板残余应力的分布有较大的影响。优化力学边界条件，有望使层间冷却时间大幅度改善多层多道焊厚板的整体残余应力水平。

层间冷却时，L1焊缝中心残余应力比局部不冷却时减小，是因为L1两端固定，母材在冷却过程中只能在焊缝位置收缩；而对于L2，由于两端自由，在两种工况下，母材都可以在整个x方向膨胀或收缩，因此层间冷却时间对L2位置的残余应力几乎没有影响。

4 结 论

本文研究了热弹-塑性有限元在多层多道焊数值模拟中的应用，建立了厚板多层多道焊的有限元模型，对层间不冷却和层间冷却200 s两种工况下多层多道焊厚板的残余应力和变形进行了计算和讨论，根据本文的研究，可得到如下结论：

（1）层间冷却对多层多道焊厚板的焊接变形影响不大；

（2）层间冷却主要影响两端固支剖面的残余应力分布，对两端自由剖面残余应力的分布影响不大；

层间冷却时间的大小和力学边界条件的选取如何影响多层多道焊厚板的残余应力和变形，是下一步研究方向。