异常信息的智能分类算法研究
2021-11-01马宗方马祥双
马宗方,马祥双,宋 琳,罗 婵
(西安建筑科技大学 信息与控制工程学院, 西安 710055)
0 引言
智能信息处理是信号与信息技术领域一个前沿的富有挑战性的研究方向,它以人工智能理论为基础,侧重于信息处理的智能化,包括计算机智能化(文字、图象、语音等信息智能处理)、通信智能化以及控制信息智能化[1-3]。然而在实际应用中,各种复杂因素可能会导致采集到的数据信息是不完整的。例如,在气象数据的采集过程中,由于传感器故障或者在数据传输过程中信号受到噪声干扰,就会造成某一段时间内的数据缺失;在填写调查问卷时,调查者不愿意回答那些涉及到个人隐私的问题,这样就导致无法获取这部分信息。由于大多数传统的分类器不能直接处理含有缺失值的数据集,因此有大批学者研究并提出了适用于不完整数据的分类算法[4-5]。其中,最简单的就是删除含有缺失值的样本或者删除缺失值所在的属性项,然后再用传统的分类器分类[5]。但是删除法仅适用于缺失率不到5%的数据集,并且删除属性项可能会改变数据分布,进而会影响算法分类性能。最为常见并且有效的处理不完整数据分类问题的方法是插补法,就是通过合理的估值来填补缺失数据,这样就能用基础分类器对带有估计值的完整数据分类[5]。
1987年,Little和Rubin[7-8]针对数据缺失机制提出了3种不同类型的缺失情况:完全随机缺失(MCAR,missing complete at random)、随机缺失(MAR,missing at random)和非随机缺失(MNAR,missing not at random)。目前对缺失数据的研究主要集中在MAR和MCAR上。在众多的缺失值插补方法中,主要分为单值插补和多值插补。常用的单值插补方法是均值插补(MI,mean imputation)[9],其主要思想是根据已观测属性值的平均值代替缺失值,但是均值插补没有考虑到样本不同属性之间的联系并且可能会改变数据的分布。K近邻插补(K-nearest neighbors imputation, KNNI)[10],主要根据数据中缺失样本的完整变量找出与其距离最近的K个样本,然后利用距离函数分别计算这K个样本与该样本的距离加权这K个样本对应不完整样本的缺失项得出估计值。FCM 插补(FCMI,fuzzy c-means imputation,)[11]是首先对数据集用FCM聚类,然后用聚类后的类中心和隶属度来估计不完整样本的缺失值。多值插补方法,也就是为缺失值提供多个版本的估计值来表征估计值的不精确性。最早提出的多重插补方法[12]是对缺失数据集插补m次(m>1),每次插补后得到一个完整的数据集,最终可以得到m个完整的数据集,接着对这m个完整数据集进行分析,综合这m次插补结果,做出统计推断。一种基于随机森林的多值插补方法[13]是通过构造大量的回归树与随机树来给缺失值提供多个版本的估计值。
传统的基于插补的不完整数据分类方法会将待测样本分配给确切的类别。然而由于数据的缺失,样本的类别可能变得很模糊,而这些方法并没有考虑到这种数据缺失对分类的影响。在这种情况下如果强硬的划分样本给某一单类,这会增加错误分类的风险。在这种情况下,如何去表征数据缺失引起的不确定性是亟待解决的问题。
证据推理[14-19],是由Dempster在1967年最先提出的,后来由Shafer推广并形成的理论,所以也称为Dempster-Shafer理论。因为证据理论具有处理不精确和不确定信息的优势,因此广泛应用于数据分类、专家系统和信息融合等领域。文献[20]提出了一种基于证据推理的不完整数据分类方法(PCC,Pototype-based credal classification)。PCC首先用不同类别的中心分别估计缺失值来表征估计值的不精确性,然后对带有不同版本估计值的不完整样本的分类结果折扣融合,最后将那些难以确切划分类别的样本分配到合适的复合类来表征由于缺失值引起的类别的不确定性。
本文提出了一种不完整数据智能分类方法,该方法依据不完整样本近邻中的类别信息自适应的估计缺失值,也即采取单值插补与多值插补相结合的混合插补策略,并且在证据推理框架下,提出一种新的信任分类方法来合理的表征不完整样本类别的不确定性,并有效地避免错误分类的风险。
1 背景知识
1.1 K近邻插补
K近邻插补是用不完整数据的已知属性在完整数据中找到K个近邻,然后用它们估计不完整数据对应的缺失值。假设测试样本集X={x1,x2,...,xn}利用训练样本集Y={y1,y2,...,yn}在类别识别框架Ω={w1,w2...,wc}下进行分类,其中xi是测试样本集中的第i个样本。目标xi已知T个属性值。首先,利用xi已知属性计算它与训练集Y中的每一个样本yi(1,2,...,n)之间的欧氏距离,距离公式如下:
(1)
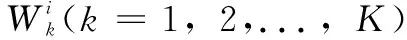
(2)
由此,我们可以得到,距离xi越近的近邻所占的权重越大。最后对xi缺失值对应的K近邻的已知属性值加权求和,得到的结果即为xi的估计值。
1.2 信任函数的理论基础
信任函数是由Shafer在其独创的数学证据理论中引入的,该理论也被称为证据理论 (evidence theory),简称DST。该理论已经在信息融合、模式识别以及决策分析等领域得到了广泛应用。
假设Ω是一个识别框架,或称为假设空间。在证据推理中,识别框架从Ω={ω1,ω2,...ωc}扩展到幂集2Ω,其包含了Ω所有的子集。一个证据的基本信任分配(BBA, basic belief assignment),指从幂集2Ω到[0,1]上的一个映射函数m(.):2Ω→[0,1](又称为基本信任函数或者mass函数),并满足以下条件:
(3)
如果m(A)>0,则称A为焦元。如果m(A)=max(m(·)),则称A为主焦元。
设在识别框架上有两个独立证据B和C,它们的mass函数分别为m1,m2的Dempster合成规则为:
(4)
其中:K为归一化常数即矛盾因子:
(5)
由于满足交换律和结合律,即可推广到n个互相独立的证据,Dempster合成结果为:
(m1⊕m2⊕...⊕mn)(A)=
(6)
其中:
(7)
尽管证据理论在解决不确定性的问题方面具有一定优势,但是在实际应用中,Dempster组合规则不适用于高冲突证据,在这种情况下常常会得出与常识相悖的结论。为此,许多学者提出了改进的组合规则。大致分为两种:1)改进组合规则;2)融合前对证据进行修改。在改进规则中,一般认为不合理融合结果主要由于DS规则对高冲突信息的分配不当造成的,针对此一些学者提出了改变冲突信息分配方式来改进规则。在证据修改方法中,一般认为高冲突证据在融合过程中每个证据的权重是不一样的,要先对证据加权处理,然后再融合。
2 不完整数据智能分类算法
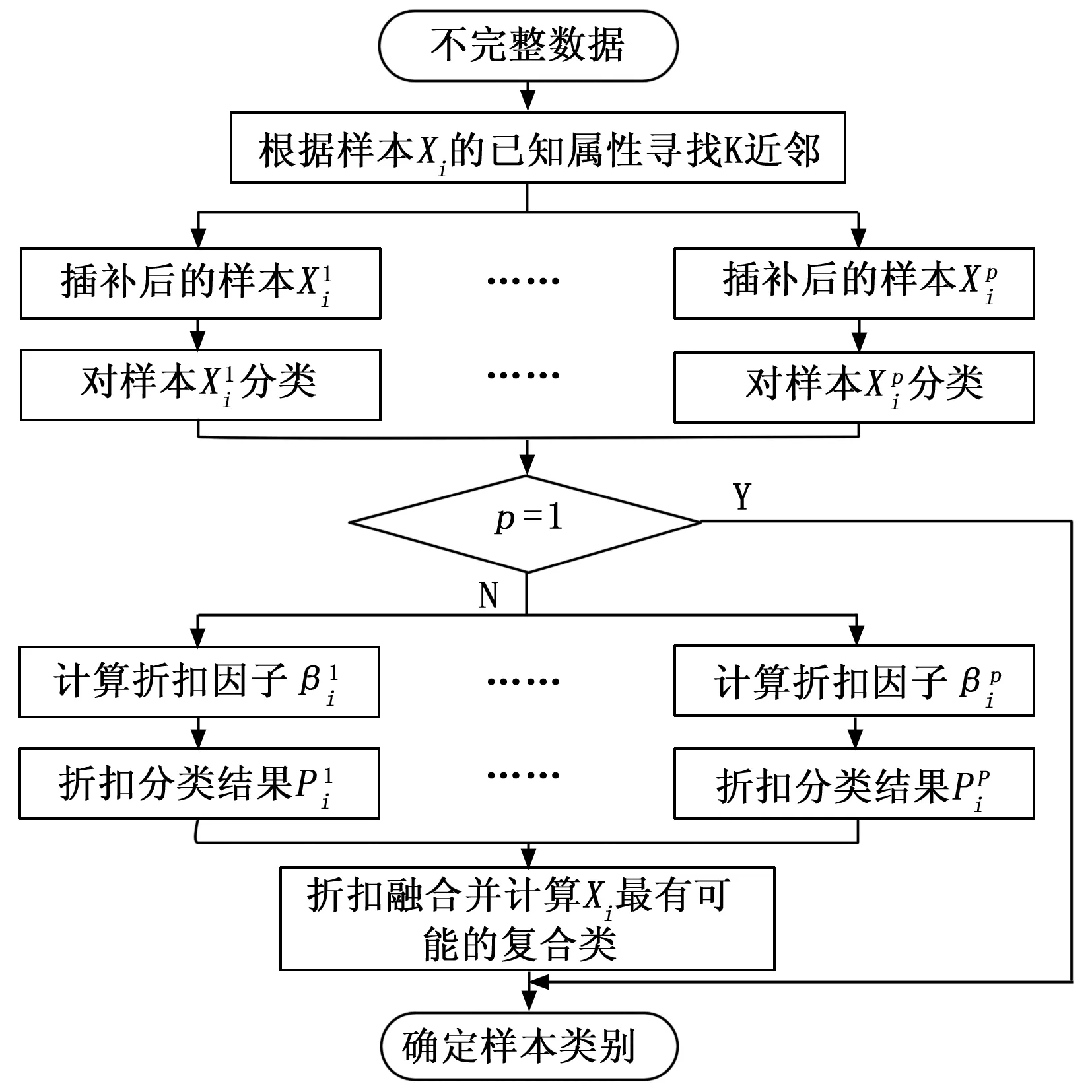
针对不完整数据分类问题,本文提出了一种不完整数据智能分类方法。它主要包含3个步骤:1)自适应插补;2)折扣分类结果;3)全局融合。
2.1 自适应插补
假定训练集为Y={y1,...,ym},共包含了c个类别,并且训练样本都是完整的;测试集X={x1,...,xn},并且测试样本都存在缺失值。用缺失样本xi(i=1,...,n)的T个已知属性在训练集中寻找K近邻。首先计算xi与每一个测试样本yj(j=1,...,m)之间的欧式距离,如下所示:
(8)
其中:xia和yja和分别表示测试样本xi和训练样本yi的第a个属性。计算得出m个距离值,对这m个距离从小到大排序,其中最小的K个距离对应的K个样本{y1,...,yk,...,yK}即为xi的K近邻。这K个近邻可能来自于p(1≤p≤c)个类别{ω1,...,ωg,...,ωp}。当p=1时,也即近邻都来自于同一个类,在这种情况下样本xi就有很大的可能属于这个类,那么就用这些近邻插补xi得到一个精确的估计值。当p>1时,也即近邻都来自于多个类,说明样本的数据缺失导致它的类别变得很模糊,为了降低这种数据缺失带来的不确定性的影响,在这种情况下我们采取多值估计策略,用这不同类别的近邻分别估计xi的缺失值。
此外,由于每个近邻与不完整样本间的距离不同,因此对估计缺失值的贡献也就不同,也即距离不完整样本越近的近邻在估计缺失值时的比重应该越大。对于不完整样本xi来说,我们用它的K近邻中属于类的近邻来估计缺失值,那么用这些近邻估计缺失值ωg(g=1,...,p)时的权重计算如下所示:
(9)

(10)
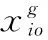
对样本xi估计的p个版本用用标准分类器分类。然而,不同版本估计值的准确性是不同的,这会导致其分类结果的可靠性不同。
2.2 折扣分类结果

(11)
如果p=1,也即样本xi的K近邻均来自同一个类别,那么带有唯一估计值的不完整样本就会得到特定的分类结果,在这种情况下,样本xi分配给结果中支持所属类别概率最大的那一类。
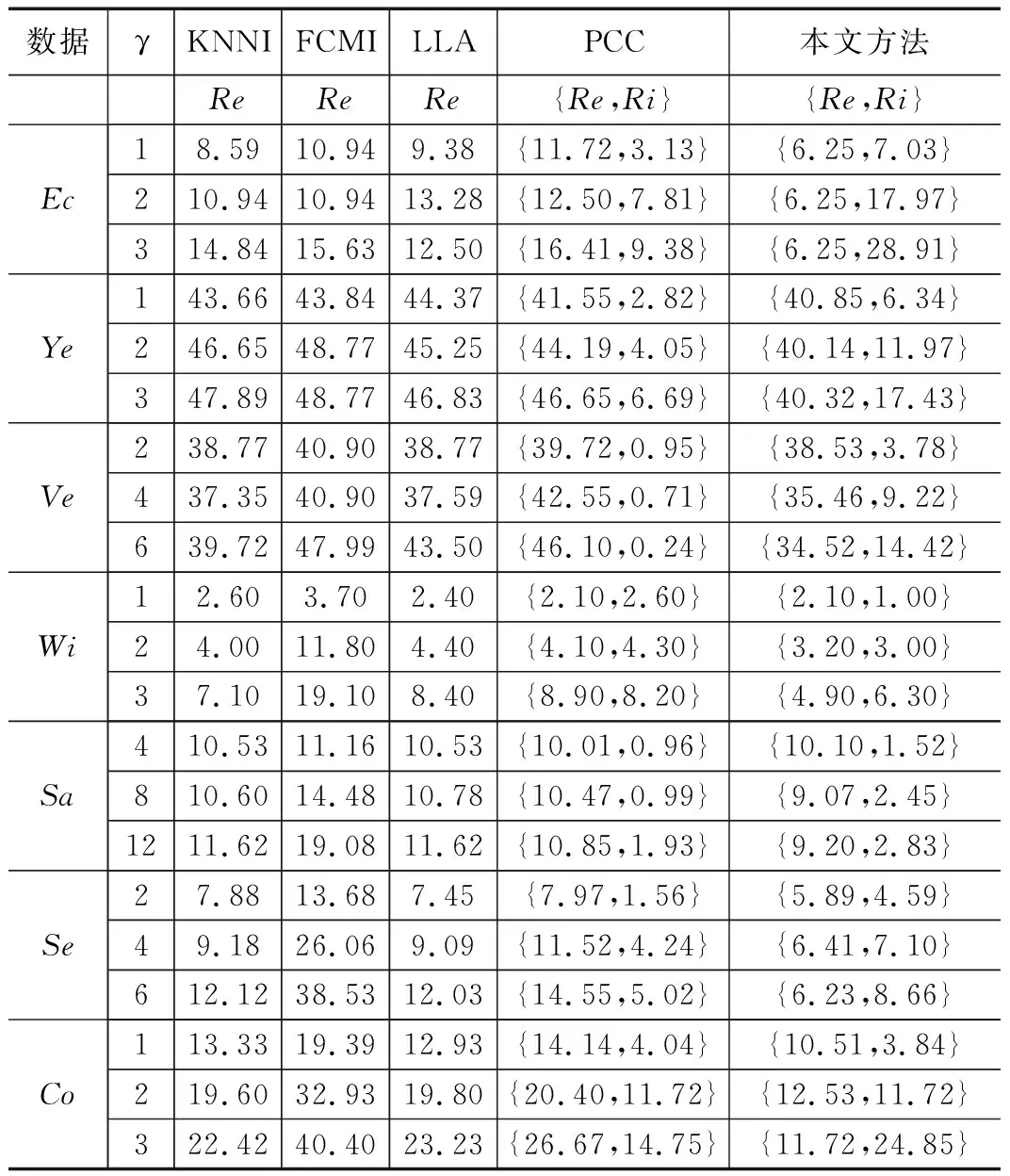
如果1 (12) 其中: (13) (14) (15) 基于可靠性的折扣规则通过修改证据能够有效地降低证据间的冲突,在这种情况下就可以用DS直接融合这些折扣后的证据。然而,由于数据缺失会带来不完整样本类别的不精确性,为了表征这种不精确性并且降低错误分类的风险,本文提出一种新的全局融合策略。 这p个分类结果可能将样本目标分给不同的类别。由于折扣后的分类结果只有单类和由整个辨识框架表示的完全未知类,也即每个表示分类结果的BBA中只有单焦元和完全未知焦元。为此我们要确定样本目标xi最有可能属于的复合类。假设这p个分类结果支持样本xi属于q个不同的类{ω1,...,ωr,...,ωq},那么根据这些分类结果所属类别将它们划分成q个不同的群组。对于样本目标xi来说,假定有s个分类结果支持它属于ωr,然后定义如下函数来计算支持样本xi分别属于这q个类最大的m(.)值。 mi(ωr)=max{mi1(ωr),...,mis(ωr)},r=1,...,q (16) 然后通过下式计算得到拥有最大信任值支持样本xi属于的那个类ωmax。 (17) 接着通过下式找到样本xi最有可能属于的复合类中的单类。 Λi={ωmax∪ωr|mi(ωmax)-mi(ωr)≤α} (18) 最后,在DS融合的基础上,定义如下规则融合这多个版本的分类结果,如下所示: mi(A)= (19) 其中: (20) 其中:α为控制不精确率的参数,α越大,就会计算越多的复合类,从而会增加分类结果中的不精确性,但同时也会有效降低错误分类的风险。在实际应用中,α可以根据可接受的不精确率来选择,本文默认为α=0.3。在实际应用中,对于分配到复合类中的样本,可以根据其他的信息来进一步的准确划分它们的类别。 为了清楚直观地表示算法的基本原理,我们绘制了算法的流程,如图1所示。 图1 本文方法算法流程图 本文从UCI数据库(http://archive.ics.uci.edu/ml)选取了7个标准数据集进行测试。Ecoli(Ec)是关于蛋白质定位的数据集,Yeast (Ye)为预测蛋白质细胞定位位置数据集,Vehicle (Ve)是关于车辆轮廓特征的数据集,Wifi (Wi)是无线数据定位数据集,Satimage (Sa)数据集是关于卫星图像的像素值,Segment (Se)是一个图像分割数据集,Connectionist (Co)是一个关于英式元音识别数据集。这些数据的类别在3~11类之间,属性个数在7~36之间,样本数在255~6 435之间,因此这些数据是UCI数据库中比较有代表性的数据,这样也能够更加全面并充分地验证不同算法在处理不同类型数据集性能。这些数据的基本信息,包括数据集的名称和简写、类别数、属性数以及样本数,如表1所示。 表1 数据集基本信息 本文方法用以上的真实数据集分别与KNNI[10]、FCMI[11]、LLA[18]、PCC[19]算法进行对比分析。同时采用了K-NN、EK-NN和决策树DT三种标准分类器进行实验。在本文方法算法中设置不精确率的阈值α=0.3,近邻数K=11。 实验中,我们随机选取每个数据集的一半数据作为训练集,另一半数据作为测试集,然后对测试集进行随机缺失处理(MCAR)。每个测试样本有γ个缺失属性值,随机分布在样本的各个属性上。实验以分类器在测试集上的最终分类误分率Re和不精确率Ri作为评价标准,Re=Ne/N,Ri=Ni/N,其中N表示样本数量,Ne表示错误分类的样本数量,Ni表示分配到复合类的样本数量。Re是用于评估分类结果中错误分类样本所占比重,Re值越小说明误分的样本越少,算法性能越好。Ri是用于评估分类结果中划分到复合类的样本所占比重,该值越大,说明划分到复合类中样本越多,这样并不利于决策,因此根据具体实际应用的要求,该值应在一个可接受范围内。 不同方法用K-NN分类器分类后的结果如表2所示。由于传统的概率框架下的方法KNNI、FCMI和LLA得到的是确切的类别输出,因此只有错误率,而PCC和本文方法在证据框架下能得到不精确输出表征不确定性,因此存在有不精确率。从实验结果可以看出,本文方法得到了比KNNI、 FCMI、 LLA和PCC更低的误分率。当每个测试样本中缺失值的个数 (γ) 增加时,所有分类器的错误率也会增加,这是由于数据缺失会影响分类的性能,缺失的数据越多,分类性能也就越差。在本文方法中,一部分难以划分类别的样本被分配到复合类中,这能够表征缺失值引起的类别的不确定性,同时这种谨慎的决策方式能够有效降低错误分类的风险。 表2 不同算法用K-NN的分类结果 由于本文方法以及对比方法都是基于插补的不完整数据分类方法,也即先补全缺失数据,再用能够分类完整样本的基础分类器分类。为了研究使用不同分类器情况下不同方法的性能,这里分别使用EK-NN和DT作为基础分类器分类不同数据集,实验结果如表3和表4所示。从实验结果可以看出,使用EK-NN分类器相较于使用其他两种分类器的分类结果更优,当然这主要由分类器本身的分类性能决定的。当然,虽然使用不同分类器得到的分类结果不同,但是本文方法在使用不同分类器情况下的整体分类性能要优于其他方法。根据实验结果,在实际应用中,本文方法在执行过程中推荐使用EK-NN或者K-NN分类器。 表3 不同算法用EK-NN的分类结果 表4 不同算法用DT的分类结果 本文算法主要有两个参数:K和α。其中K用于表示用于估计缺失值的近邻个数;α用于判别本文算法中待测不完整样本是否会被划分到复合类的阈值,因此它也能够用于调节本文算法中错误率和不精确率。本小节主要是通过实验研究这两个参数对本文算法以及其他方法的影响。 3.3.1K值的影响 由于这些对比方法中只有KNNI、LLA以及本文方法存在该参数,因此这里选择部分有代表性的数据集来测试K值对这些算法性能的影响。如图2所示,X轴表示分类器K的个数从5~15,Y轴表示KNNI、LLA和本文方法算法不同分类器错误率和不精确率。从图中可以看到,与其他方法相比,本文方法的错误率更低,并且不精确率也在可接受的范围内。可以看到,随着K值的改变,不同方法的分类结果有所变化。本文方法受K值的影响比较小,这也证实了本文方法对于K值的选择具有一定的鲁棒性。 图2 选择不同的K值时不同方法的分类结果 3.3.2 阈值α的影响 由于阈值α只存在于本文方法中,因此这里选择两个代表性的数据来研究阈值α对本文方法的影响,图3显示的是阈值α取不同值时本文方法的分类正确率和不精确率,其中X轴表示α的不同取值,Y轴表示本文方法的错误率和不精确率。从图中可以看到随着α值的增大,错误率在降低的同时不精确率在逐渐升高。α的值过小会导致很多样本被错误分类。当然,α的值并不是越大越好,因为这样会使大量样本分配到复合类,这并不利于决策分析。在实际应用中,α可以根据可接受的不精确率取值。 图3 选择不同阈值α时本文方法的分类结果 本文提出了一种不完整数据智能分类算法,该方法通过自适应插补来提高估计精度,同时在证据推理框架下将难以划分类别的不完整样本分配到相应的复合类,这样能够有效地表征缺失值带来的不确定性,同时降低错误分类的风险。虽然实验结果证实了本文方法分类不完整数据的有效性,但是本文方法的插补是基于K近邻的,这需要大量的计算,在未来的工作中会考虑研究一种快速的K近邻插补技术,在保证估计精度的同时降低算法计算K近邻所产生的计算量。
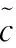
2.3 全局融合

3 实验及结果分析
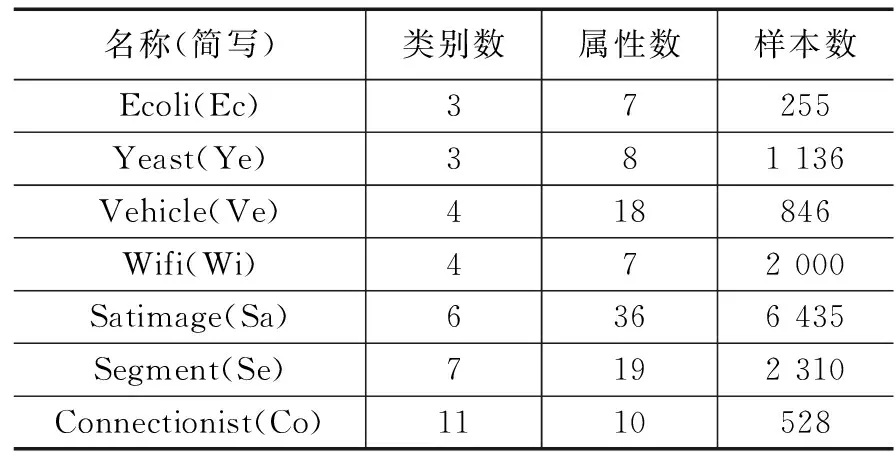
3.1 数据集
3.2 对比实验


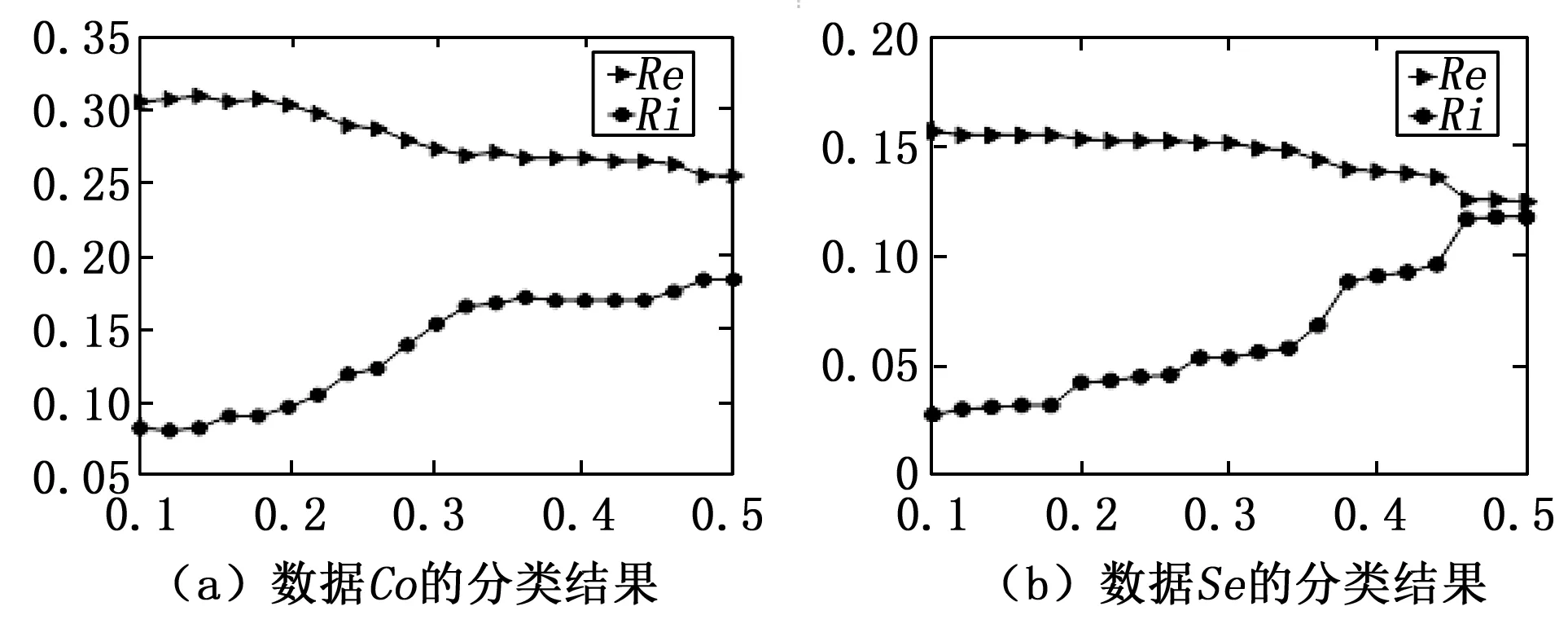
3.3 算法参数对分类性能的影响

4 结束语
