基于最小HDOP选站下的到达时间差定位算法
2021-10-30王腾辉武建锋焦喜康朱靖川
王腾辉,武建锋,焦喜康,朱靖川
基于最小HDOP选站下的到达时间差定位算法
王腾辉1,2,武建锋1,焦喜康1,2,朱靖川1,2
(1. 中国科学院 国家授时中心,西安 710600;2. 中国科学院大学 电子电气与通信工程学院,北京 101048)
传统蜂窝网络系统虽支持基于到达时间差(TDOA)的定位方法,但是精度较差。第五代移动通信(5G)可在室内定位分配系统中提供准确的多个TDOA测量值,可显著提高室内定位能力。随着5G微基站的大规模普及,目标终端从基站一侧可选择的测量值也越多,按照传统方法直接进行解算,测速运算量大且无法剔除误差较大的观测值。本文提出一种定位基站最优组合方法,使用广度优先搜索(BFS)筛选出水平精度因子(HDOP)最小的定位基站组合,并考虑每个TDOA测量误差具有不同的方差,采用加权最小二乘算法估计在基站最优组合条件下目标终端的位置。通过仿真分析和试验验证,基于最小HDOP选站下的到达时间差定位算法在保证了定位准确度的前提下,单次定位解算速度提高了51.14%,显著提升了定位响应速度。
到达时间差;第五代移动通信;水平精度因子;广度优先搜索;最小二乘
0 引言
室内定位对于基于位置的服务,物联网和电力服务等非常重要[1]。目前市场流行的几种定位技术包括蓝牙信标技术、超宽带无线技术以及基于蜂窝网络定位技术。其中,蓝牙信标技术是目前主流的一种室内定位方案,该技术最大的优点是设备体积小,容易集成于手机等移动设备中,但对于复杂的空间环境,蓝牙系统容易受到噪声信号干扰,且蓝牙器件和设备价格比较昂贵[2-3]。超宽带(UWB)无线技术是近年来提出的室内无线定位技术,具有定位精度高、穿透力强等优点,然而布局该系统成本太高[4-5]。5G定位技术的出现能够满足高精度定位对无线网络的需求[6],5G的毫米波通信具有高频、高带宽的特点,有利于提高多径分辨率,不易受噪声信号干扰[7],并且5G具有成熟的室内分配方案包括5G分布式天线系统(DAS)与5G数字室分,通过利用旧的DAS完成室内5G覆盖,可以有效地降低布局成本[8]。
LTE移动通信系统提供的到达时间差估计技术使用定位参考信号(PRS)进行测距,PRS部分响应信号的带宽只有1.4~20 MHz,带宽的有限无法保证定位的精度[9-13]。而在5G系统下,PRS信号的带宽可以提高到100 MHz[14],因此5G系统可以在较大的带宽以及连续的上下行信号上提供高精度的TDOA(time difference of arrival)测量值。微基站的大规模普及使得从基站一侧可以提供的测量数据十分充 裕,在这种情况下,对目标的定位问题由原来的非线性方程精确求解问题转换成了非线性最优化估计问题[15]。目前有很多定位算法用于TDOA测量方程的解,这些算法可以分为迭代算法和闭式求解算法,Taylor级数展开法是一种常用的迭代算法,当给定初始位置不准确时,迭代算法不能保证收敛,即出现较大误差[16],闭式求解算法可以避免收敛问题,最常用的闭式算法为两步加权最小二乘(WLS)算法[17],该算法在TDOA误差足够小时,可达到克拉美罗下界。当存在大量TDOA测量值时,按照传统方法直接解算运算量大且有误差较大观测值的干扰[18-22]。本文在使用两步加权最小二乘解算前,对误差较大的TDOA观测值进行剔除,从而提高定位精度与响应速度。

1 基于到达时间差的定位方法
1.1 TDOA定位原理




1.2 基于TDOA的定位解算算法
由于二维定位至少需要3个基站,所以TDOA的解算算法只能基于基站个数至少是3个才可以进行定位,实际工程中应用最广的为最小二乘。最小二乘算法大致可以分为两类,即具有解析表达式的算法和递归算法。二维情况下,Chan氏算法分为三基站定位和三基站以上定位两种情况,两步加权最小二乘近似一个最大似然估计器。
1.2.1 基站个数为3的情况


1.2.2 基站个数大于3的情况
① 第一次加权最小二乘估计
TDOA噪声的线性方程为


② 第二次加权最小二乘估计


建立线性方程组:
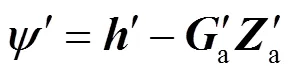


1.3 水平精度分析
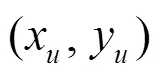

令方向余弦


式(13)表示为矩阵形式为
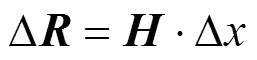
考虑每个基站的TDOA测量误差不同,因此不同于普通最小二乘,使用加权最小二乘解算,解算式为

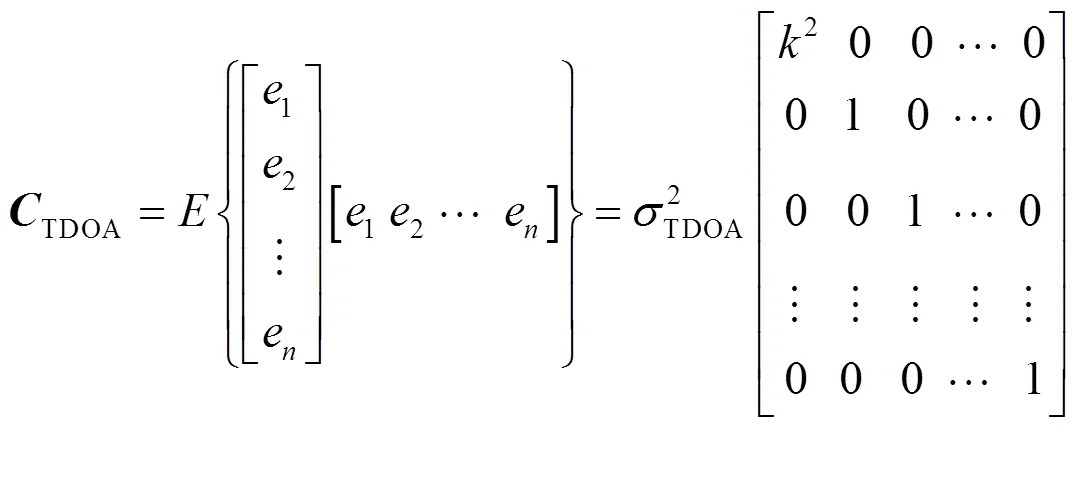
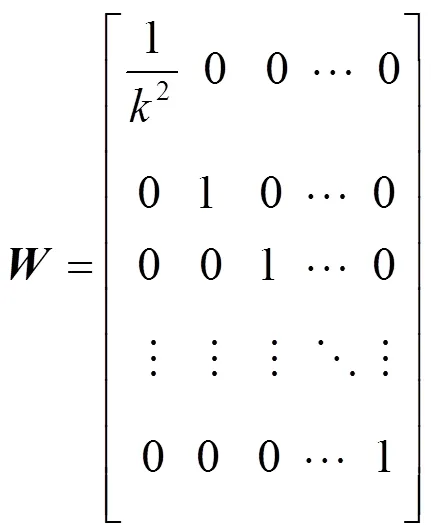



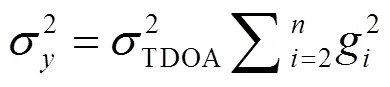
HDOP是描述水平坐标精度的误差程度,考虑实际工程中每个TDOA测量误差不同,故使用加权最小二乘得出此方法下的HDOP表达式:
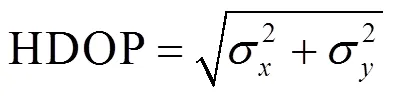
1.4 基于广度优先搜索的选站方法
微基站的大规模普及使得终端接收机附近存在多个基站,接收机一侧接收到的测量数据就变得十分充裕,在这种情况下,通过选取对定位结果最优的基站组合,不仅能剔除误差较大的观测值,也能提高解算速度。
广度优先搜索(BFS)作为搜索算法的一种,被广泛应用在图论算法模型中,图论中的Dijkstra算法和Prim最小生成树算法都是由广度优先搜索演变而来[28],广度优先搜索算法的核心思想是从当前的节点向外扩展,用数据结构中的栈维护可以采用的节点,直到所有节点都被访问,栈组中存在的节点即是最后需要的节点。

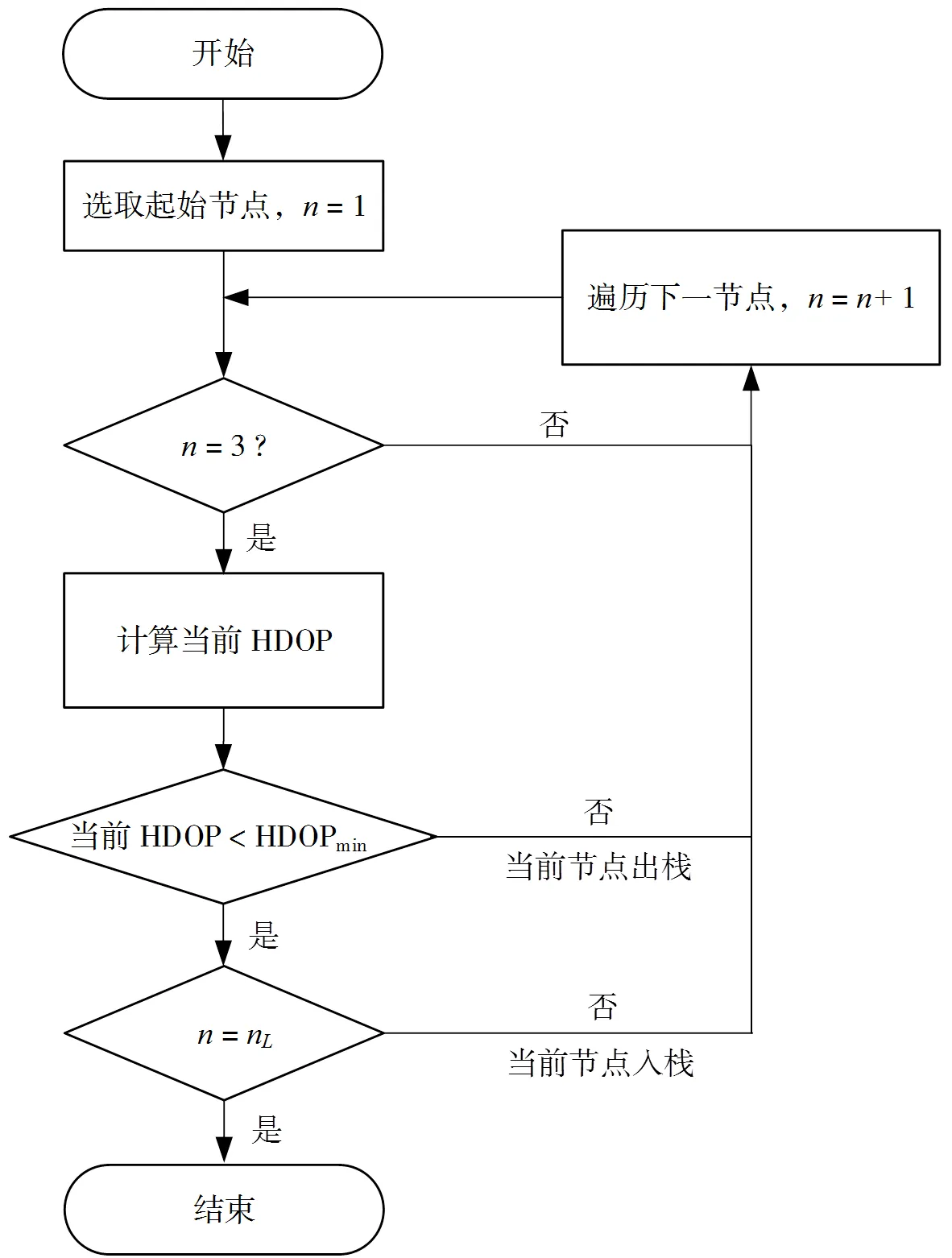
图1 BFS算法选站流程图
2 仿真结果与分析
为分析基于最小HDOP准则下的选站组合对定位精度影响,根据中国科学院国家授时中心试验厂区的真实场景,建立一个模拟场景,真实的场景如图2所示,开发的模拟场景俯视图如图3所示。真实场景试验区为50×30 m的长方形区域,建立笛卡尔坐标系。

图2 地下试验场真实场景
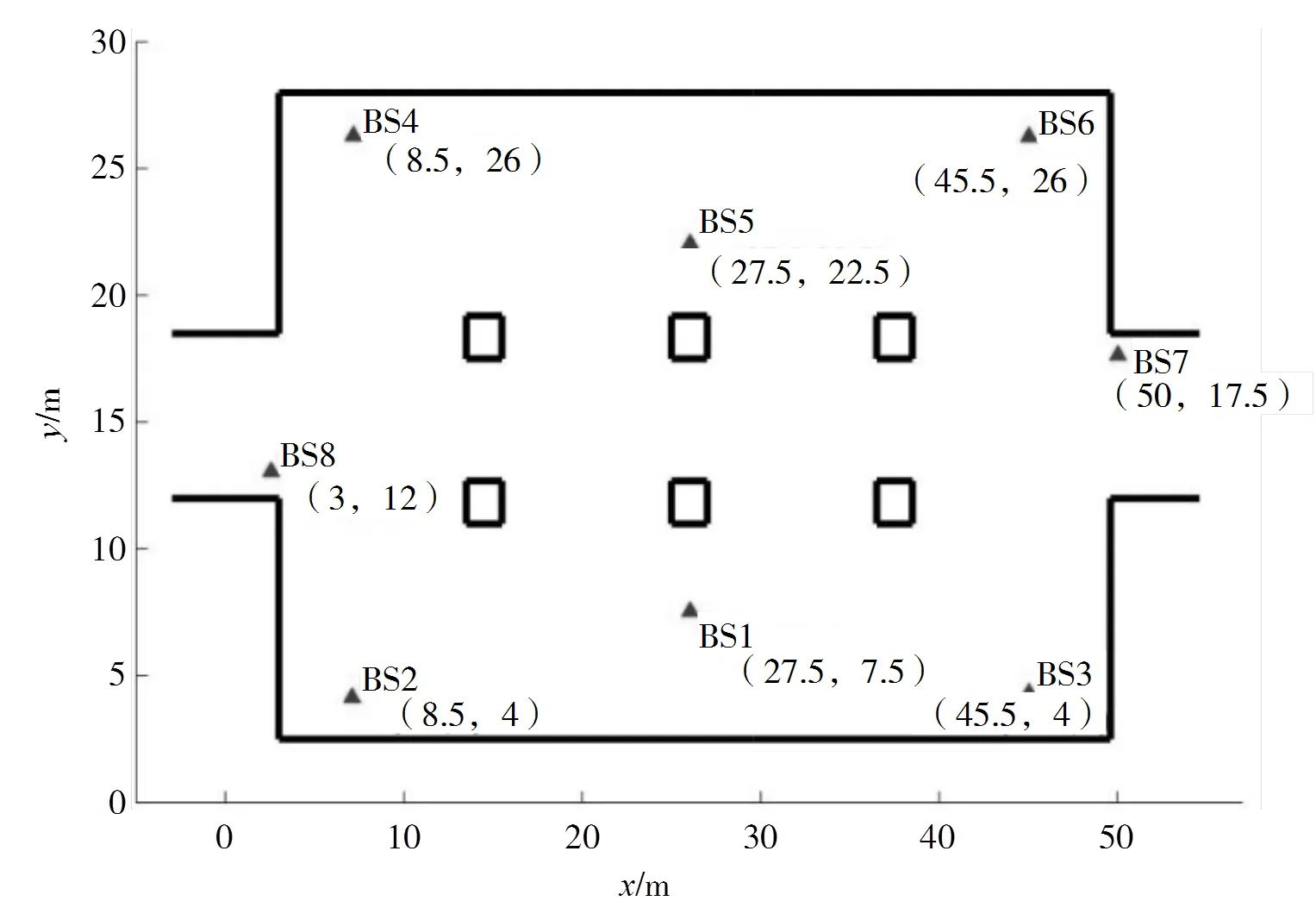
图3 模拟场景俯视图
在图3中笛卡尔坐标系以米为单位,根据试验场真实环境,选取两个具有代表性的测试点,分别位于场景右半边A点和左半边B点,如图4所示。

图4 A、B点俯视图
图4中圆点为测试坐标点,小三角为基站坐标点,其中,距离A点最近的3个基站为BS3,BS6,BS7,距离B点最近的3个基站为BS1,BS2,BS8。
使用广度优先搜索算法对A点筛选最优定位基站组合,首先选取距离终端A点最近的基站BS7,再依次遍历。按照图1的算法流程,选出的A点最小HDOP的基站组合BS1,BS3,BS5,BS6,BS7。为了验证算法的准确性,对A点的几组基站组合单独进行HDOP计算,由表1可以看出,提出的广度优先遍历算法选出的基站组合HDOP值最小,值为1.54,距离A点最近的3个基站BS3,BS6,BS7的HDOP为2.24,全站参与下的A点HDOP值为1.61。

表1 A测试点的基站组合及HDOP值
同理,对B点筛选最优定位基站组合,首先选取距离B点最近的基站BS1,按照图1的算法流程,选出的B点最小HDOP的基站组合BS1,BS2,BS8。选取的最优基站组合是距离B点最近的3个基站,为验证算法准确性,在BS1,BS2,BS8基础上增加B点周边基站,计算各组合HDOP。由表2可以看出最优基站组合HDOP值为1.87,且为距离B点最近的3个基站,在此基础上增加基站数量,都会增大HDOP的值。

表2 B测试点的基站组合及HDOP值



图5 本次测试的主要设备
表3和表4为A测试点下的最优基站组合与全站的测试结果,其中,在499次的有效测试点中,最优组合的最大单次解算耗时为0.354 s,平均单次解算耗时为0.178 s。在498次的有效测试点中,全站参与下的最大解算耗时为0.423 s,平均单次解算耗时为0.312 s,可以看出本文所提算法在效率上提高了42.94%。

表3 A点最优组合基站的测试结果
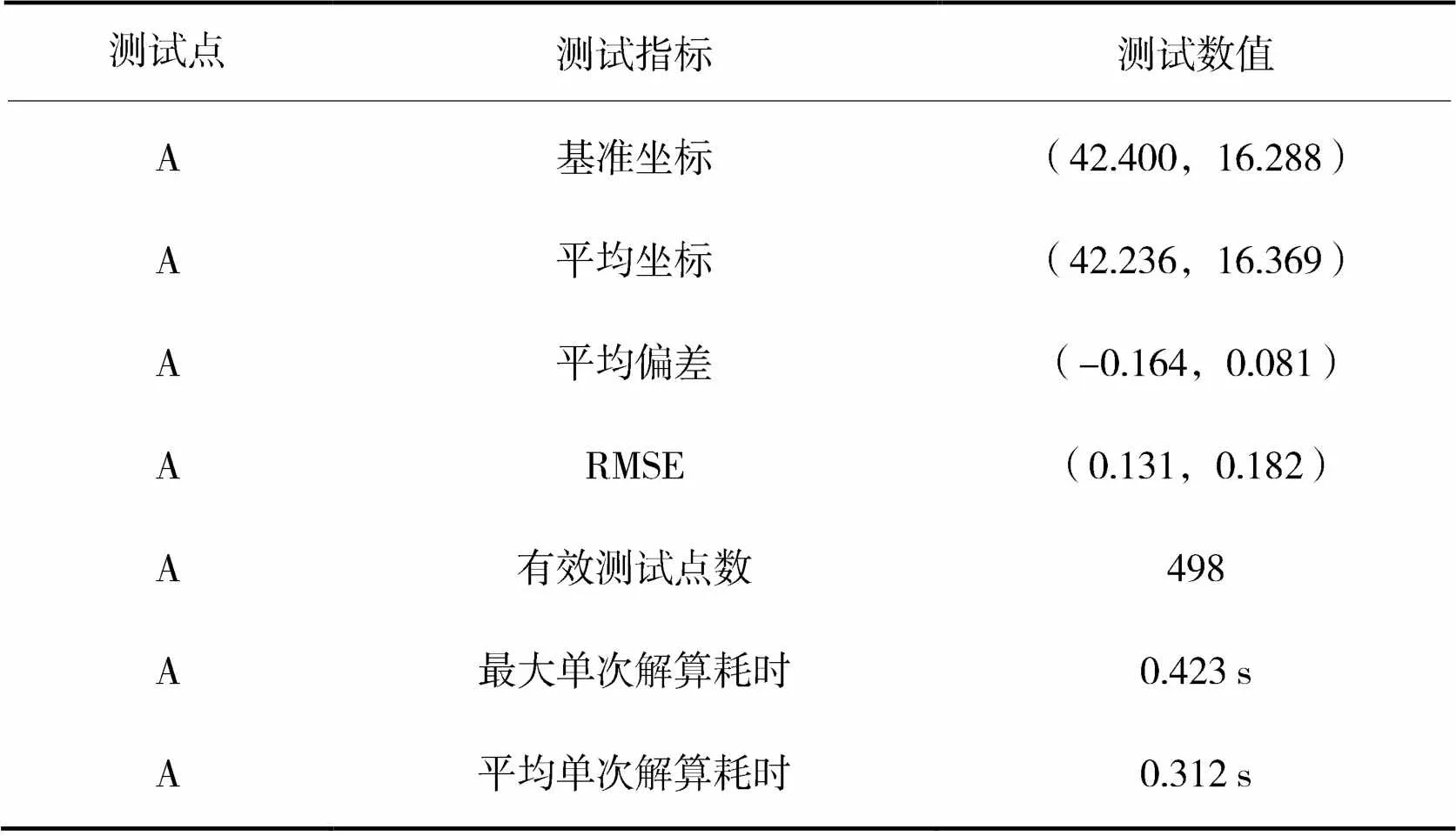
表4 A点全站的测试结果
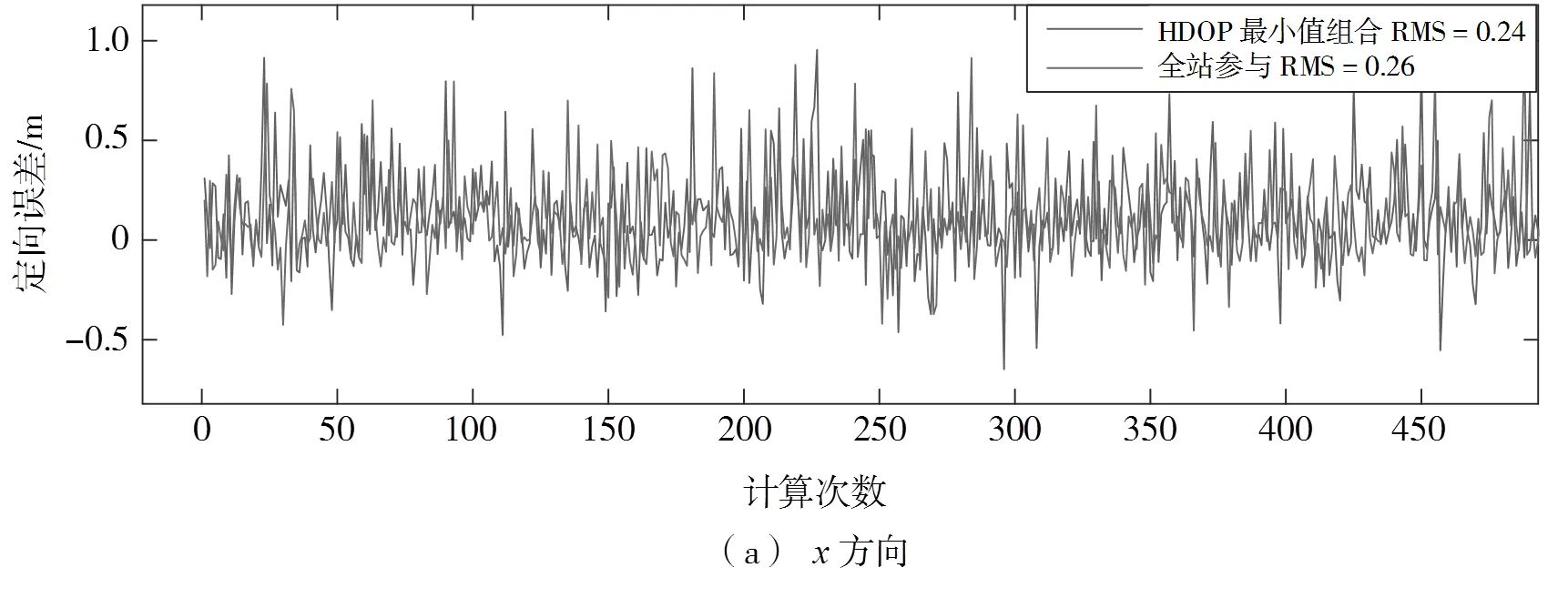
图6为A点在最优基站组合与全站组合下单方向误差比较,可以看出,最优基站组合方向和方向上的均方根误差均小于全站参与,最优组合下的方向平均偏差为0.159 m,方向平均偏差为0.075 m,全站组合下的方向平均偏差为-0.164 m,方向平均偏差0.081 m。

对B点进行测试,最优基站布局对应BS1,BS2,BS8坐标位置,5G终端对应B点坐标位置,对最优基站组合下终端解算观测次数为500次。
表5和表6为B测试点下的最优基站组合与全站的测试结果,其中,在495次的有效测试点中,最优组合的最大单次解算耗时为0.234 s,平均单次解算耗时为0.128 s。在494次有效测试点中,全站参与下的最大解算耗时为0.354 s,平均单次解算耗时为0.262 s,可以看出本文所提算法在效率上提高了51.14%。

表5 B点最优组合下的测试结果

表6 B点全站组合下的测试结果
图7为B点在最优基站组合与全站组合下单方向误差比较,可以看出,最优基站组合方向和方向上的均方根误差均小于全站参与,最优组合下的方向平均偏差为0.348 m,方向平均偏差为-0.069 m,全站组合下的方向平均偏差为-0.350 m,方向平均偏差为0.065 m。
3 结语
本文通过使用广度优先遍历搜索筛选出HDOP最小的定位基站组合,在5G系统大量TDOA观测量的前提下,剔除了误差较大的观测量,能够在保证定位精度的前提下提高定位响应速度。特别地,当最优定位基站组合为距离目标终端最近的3个基站,单次解算速度提升最快,相比全站参与解算速度提升了51.14%,说明本算法具有较强的实时性。本文通过最优定位基站组合与全基站定位误差比较,可以得出最优基站组合的HDOP值与全站HDOP值相差越大,定位精度提升越好。
[1] XIE T, JIANG H J, ZHAO X J, et al. A Wi-Fi-based wireless indoor position sensing system with multipath interference mitigation[J]. Sensors, 2019, 19(18): 1-20.
[2] KEONSOO L, NAM Y Y, MIN S D. An indoor localization solution using bluetooth RSSI and multiple sensors on a smartphone[J]. Multimedia Tools and Applications, 2018, 77(10): 12635-12654.
[3] LIE M M K, KUSUMA G P. A fingerprint-based coarse-to-fine algorithm for indoor positioning system using bluetooth low energy[J]. Neural Computing and Applications, 2020, 33(1): 1-17.
[4] 孙顶明. 基于CHAN-Taylor的室内复杂环境UWB定位算法研究[D]. 南京: 南京邮电大学, 2019.
[5] BAKKALI M E, TOUHAMI N A, ELHAMADI T E, et al. High gain 0.18μm-GaAs MMIC cascode-distributed low-noise amplifier for UWB application[J]. Microelectronics Journal, 2020, 108(1): 104970.
[6] Networks-wireless communications and networks; Researchers from tampere university of technology describe findings in wireless communications and networks (joint device positioning and clock synchronization in 5G ultra-dense networks)[J]. Computers, Networks & Communications, 2017.
[7] 3GPP.3GPP TS 22.261 v16.7.0, Service Requirements for the 5G system; Stage 1[EB/OL]. (2017-03-13)[2021-03-18].https://portal.3gpp.org/desktopmodules/Specifications/SpecificationDetails.aspx?specificationId=3107
[8] 刘翔翔, 张昌瀚. 基于地理信息系统的通信基站优化选址与布局[J]. 科技和产业, 2020, 20(9): 191-197+224.
[9] 苏煜琴, 付小宁, 张娜. TDOA localization algorithm based on lagrange constraint factor to modify the initial value of iteration[J]. 应用数学进展, 2020, 9(3): 372-381.
[10] GADKA P, SADOWSKI J, STEFANSKI J, et al. Detection of the first component of the received LTE signal in the OTDoA method[J]. Wireless Communications and Mobile Computing, 2019: 1-12.
[11] LEE K, LEE D H, HWANG W J, et al. A new D2D-Aided OTDOA positioning method for 3GPP LTE system[J]. IEICE Transactions on Communications, 2017, E100, B(3): 473-483.
[12] 王宝全. 基于TDOA参数估计的LTE定位技术研究[D]. 南京: 南京邮电大学, 2015.
[13] 李典锋. LTE及其演进系统中定位技术的研究[D]. 北京: 北京邮电大学, 2018.
[14] 3GPP.3GPP TR22.872 v16.1.0, Study on Positioning Use Cases; Stage 1[EB/OL]. (2017-03-13)[2021-03-18].https://portal.3gpp.org/desktopmodules/Specifications/SpecificationDetails.aspx?specificationId=3280.
[15] MISHRA P, KUMAR V, RANA K P S. An efficient method for parameter estimation of a nonlinear system using backtracking search algorithm[J]. Engineering Science and Technology, an International Journal, 2018, 21(3): 338-350.
[16] DINIYA J, SHONEY S. Taylor series method in TDOA approach for indoor positioning system[J]. International Journal of Electrical and Computer Engineering, 2019, 9(5): 3927-3933.
[17] KOHLER M, KRZYżAK A. Pricing of American options in discrete time using least squares estimates with complexity penalties[J]. Journal of Statistical Planning and Inference, 2012, 142(8): 2289-2307.
[18] 蒋康荣. 蜂窝网络中基于TDOA的定位算法研究[D]. 南京: 南京邮电大学, 2016.
[19] ZHANG H W, ZHENG Z, WANG W Q, et al. Source localization using TDOA and FDOA measurements under unknown noise power knowledge[J]. IET Signal Processing, 2020, 14(7): 435-439.
[20] QU X M, XIE L H. An efficient convex constrained weighted least squares source localization algorithm based on TDOA measurements[J]. Signal Processing, 2016, 119(2): 142-152.
[21] TOVKACH I O, ZHUK S Y. Adaptive filtration of parameters of the UAV movement based on the TDOA-measurement sensor networks[J]. Journal of Aerospace Technology and Management, 2019, 11(11): 1-10.
[22] 赵拥军, 赵勇胜, 赵闯. 基于正则化约束总体最小二乘的单站DOA-TDOA无源定位算法[J]. 电子与信息学报, 2016, 38(9): 2336-2343.
[23] 窦雪倩, 李华, 许博. 基于几何稀释度的多站外源时差定位最优布站方法[J]. 电子信息对抗技术, 2018, 33(5): 37-40+72.
[24] 邱明, 严勇杰, 孙蕊, 等. 基于帝国竞争优化的双目标综合决策选星算法[J/OL]. 北京航空航天大学学报: 1-12[2021-03-17]. https://doi.org/10.13700/j.bh.1001-5965.2020.0235.
[25] 王永梅. GNSS导航系统快速选星算法研究[J]. 电子设计工程, 2018, 26(3): 65-69.
[26] BANERJEE N, SANKARDEEP C, RAMAN V, et al. Space efficient linear time algorithms for BFS, DFS and applications[J]. Theory of Computing Systems, 2018, 62(8): 1736-1762.
[27] GYO X S, ZHANG Y, ZENG B T. Passive localization using time difference of arrival and frequency difference of arrivalWC[J]. Journal of Computer and Communications, 2018, 6(1): 21-29.
[28] 孟庆伟.Prim(普里姆)算法与Dijkstra(迪杰斯特拉)算法分析比较[J]. 计算机光盘软件与应用, 2013(16): 96-97.
[29] ROSADO J A D P, SALCEDO J A L, GRANADOS G, et al. Preliminary analysis of the positioning capabilities of the positioning reference signal of 3GPP LTE[C]//Proceedings of the 5th European Workshop on GNSS Signals and Signal Processing, Toulouse, 2011.
Positioning algorithm based on the time difference of arrival with the minimum HDOP of station selection
WANG Teng-hui1,2, WU Jian-feng1, JIAO Xi-kang1,2, ZHU Jing-chuan1,2
(1. National Time Service Center, Chinese Academy of Sciences, Xi’an 710600, China;2. School of Electronic, Electrical and Communication Engineering, University of Chinese Academy of Sciences, Beijing 101048, China)
The traditional cellular network system supports the positioning method based on the time difference of arrival (TDOA), but the precision is poor. The 5th-generation mobile communication (5G) can provide accurate multiple TDOA measurement values in the indoor positioning distribution system, which can improve the indoor positioning capability significantly. With the large-scale popularization of 5G micro base stations, the target terminal can select more measurement values from the base stations, then the calculation of speed measurement is much larger and the observation values with big errors cannot be eliminated while used the traditional method for the calculation directly. This study proposes a method of optimal combination for positioning base stations, which used the breadth-first search (BFS) to filter out the minimum HDOP (horizontal dilution of precision) of the positioning base station combination, and it also considered the different variance of each TDOA measurement, then used the weighted least squares to estimate the location of the target terminal. The simulation analysis and experimental verification shown that the positioning algorithm based on the time difference of arrival with the minimum HDOP of station selection ensures the positioning accuracy, and it also increased the speed of single positioning solution by 51.14%, which significantly improves the speed of positioning response.
time difference of arrival; 5G system; horizontal dilution of precision(HDOP); breadth first search; least squares estimation
10.13875/j.issn.1674-0637.2021-03-0183-14
王腾辉, 武建锋, 焦喜康, 等. 基于最小HDOP选站下的到达时间差定位算法[J]. 时间频率学报, 2021, 44(3): 183-196.
2021-04-19;
2021-05-21
二代导航重大专项资助项目(ZFS19001D(03))
