基于三维有限元理论的沥青路面可靠性分析与评价指标研究

2021-10-30张黛曦

黑龙江交通科技 2021年10期

张黛曦

(广州市交通设计研究院有限公司，广东广州 511430)

0 引言

进入21世纪以来，我国沥青路面凭借其舒适、抗滑、表面连续等优良的性能特点发展非常迅速，但伴随着沥青路面里程的不断延伸出现大量的早期病害，受设计、施工以及运营期间维修保养的局限，新建的沥青路面往往在设计使用期远未到来之前已经需要进行结构性维修。沥青路面作为一种带状多层结构物，其性能的发挥仍然可以采用结构抗力—荷载效应这种形式的结构功能函数所表征。因此，沥青路面结构也可用可靠度来度量，在整个使用期间，使路面结构性能维持在一定的可靠度之上，结构失效的概率就小，反之则大。在现有路面维修养护设计与管理过程中，采用三维有限元数值计算为手段，对在不同指标下沥青路面所蕴含的可靠度进行计算是一种重要的分析方法。

1 沥青路面可靠性分析与极限状态

1.1 可靠性原理与指标

土木工程可靠度的概念即在正常使用期内，结构完成预定功能的概率。对于沥青路面，仍然可以从这个基本概念建立其可靠度意义，对于路面在使用期间所承受的车辆荷载以及环境变化条件下提供的各项使用性能可认为是正常使用期的预定功能，这个使用性能包括表面功能方面和结构方面，设计中分别对应着平整度、抗滑以及疲劳开裂、车辙等指标。与其他土木工程结构不同的是，沥青路面结构承担着更多的功能，设计阶段需要进行多指标控制，所谓使用期末，可认为是这些功能以及结构指标衰减到各自的极限值。国内外大多数研究认为沥青路面的可靠度本质上可以用不同的设计指标表征，如当以主要承重层半刚性基层的疲劳断裂为设计标准时，可以采用半刚性层底的荷载疲劳应力不超过疲劳强度的概率来定义可靠度，这种表示概念清晰，变量容易控制，但不同设计指标之间的可靠度难以比较和换算。然而沥青路面的使用性能是一个综合的指标，在进行维修养护之前需要进行整体评价，考虑到路面的本质功能是为车辆的运行提供服务，破坏的根本原因也在于车辆的碾压，因此可以统一用路面受到的标准轴载的累计作用次数来定义沥青路面的可靠度，即路面结构能承受的累计标准轴载大于设计使用期内预计的累计标准轴载的概率。

1.2 极限状态

极限状态是进行可靠性分析的关键指标，土木工程中受一次性破坏结构的极限状态通常分为承载能力极限状态和正常使用极限状态两种类型，对于沥青路面而言，由于荷载作用的特点，其极限状态需要重新定义。沥青路面的疲劳断裂从结构的角度来讲，属于典型的承载能力极限状态，但从使用性能上看疲劳裂缝的出现并不等同于路面无法再承受车辆荷载的碾压，特别是疲劳裂缝刚出现时对使用性能影响极小，而当多条疲劳裂缝连接龟裂或受水的侵蚀出现松散、坑槽时，路面的使用性能才真正开始下降，即可靠度降低。从路面疲劳裂缝出现到使用性能下降这段时间，要维持现状路面的可靠度，维修养护的介入就显得十分重要。

2 基于有限元的沥青路面结构分析

2.1 有限元分析方法的选定

有限元法是进行结构可靠性分析的重要工具，可以在对大量数据处理的基础上研究设计参数的不确定性和随机性对计算结果的影响，可以极大的提高分析效率和精确性。常用方法包括蒙特卡罗法和响应面法。蒙特卡罗法是建立在对随机变量的大量抽样并统计的基础上获得结构失效概率的方法，是随着计算机逐步发展起来的，其基本思想是建立与分析对象有相似性的概率模型，并利用概率模型的统计特征值，如均值和方差等与数学计算问题的解答建立联系，最后求解出这些统计特征值的近似结果作为原数学问题的数值解。经过多年的发展，采用蒙特卡罗法进行模拟时可以同时用于结构失效概率和抗力参数的统计，同时模拟产生的误差也可以得到有效控制。

2.2 三维有限元建模及参数设定

由于沥青路面弹性层状体系可认为在水平方向无限延伸，无法在无限大区域划分单元，因此在利用三维有限元方法进行求解时，必须划分适当的计算范围，同时简化边界约束条件。研究采用ANSYS有限元软件进行建模，X轴和Y轴方向各5 m，根据荷载作用下路面结构层的力学响应特点，并且从节省运算速度考虑，将各层材料组成均视为均匀、各向同性的线弹性材料，并将轮印接触形状等效为边长18.5 cm的矩形。在边界条件方面，设定为左右侧UX=0，结构层底部完全约束，然后将车辆荷载的均布荷载施加为0.7 MPa。

以广州市某国道干线公路沥青路面大中修项目为依托，有限元模型建立的层状体系包括上中下三层密级配沥青层，厚度分别为4 cm、6 cm和8 cm，基层采用36 cm厚的5%水泥稳定碎石，基层下设置15 cm厚4%水泥稳定砂砾底基层，五层结构层材料的劈裂强度取值分别为1.2、1.0、0.8、0.6、0.4 MPa，结构层再往下为路床部分的土基，厚度设定为80 cm，计算点位为路面结构层顶面的弯沉值及各结构层底面的力学响应。通过对计算参数进行概率统计分析其概率分布模型和特征值。三维有限元模型及弯沉、层底弯拉应力概率分布如图1所示。

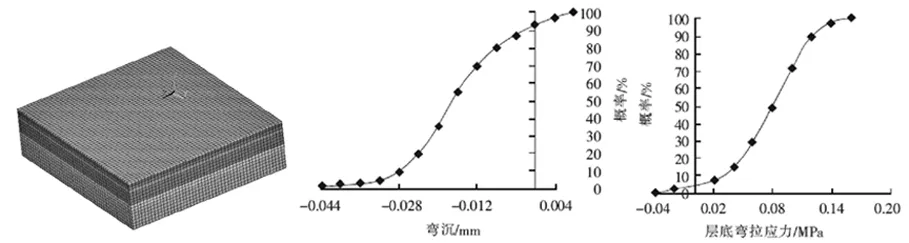
图1 三维有限元模型及弯沉、层底弯拉应力概率分布图

3 不同设计指标的当量轴次与可靠度的关系

车辆荷载的作用是路面损坏的主要影响因素，广州经济发达，往来客货车多，道路多承受着严峻的交通压力，直接影响着路面结构的使用寿命。荷载作用下路面结构产生的弯沉和层底的弯拉应力可以从路面整体和力学响应的角度反映承载能力，当采用累计标准轴载作用次数表示时，可用有限元软件计算出可靠度。为了研究车辆荷载特别是重载对现有沥青路面结构可靠度的影响，进而分析不同交通荷载累积标准轴载作用下可靠度的变化规律，研究以0.1 MPa为梯度，分别设定轮胎与路面的接触压力从0.7 MPa变化至1.4 MPa过程中以路表弯沉和基层底部弯拉应力为指标的累积当量轴次与沥青路面可靠度变化的关系，计算结果如图2所示。

图2 分别以弯沉(左)和弯拉应力为指标的不同荷载累计轴次与可靠度的关系

根据计算结果可知，无论以路表弯沉值还是层底弯拉应力为指标，沥青路面可靠度均随着荷载应力的增加而明显降低，说明超载对路面结构的损伤影响显著。其中，以弯沉为指标时，当累计当量轴次增加到150万～450万次之间时，路面结构的可靠度会急速降低到一个比较低的水平，当轴载超过这一区间后下降幅度有所减缓，基本维持不变，说明累计轴次的虽然持续增加，但敏感度却降低。超载与正常荷载相比，可靠度的降幅会约30%。当累计当量轴次大于某个限值时，再增加轴次，结构的可靠度曲线逐渐趋于水平，敏感性逐渐减小。

当以基层层底弯拉应力为指标时，在荷载应力比较低的时候，路面结构可靠度一直处于比较高的水平，随着累计当量轴次的增加并没有太大变化，仅在累计轴次超过1 200万次后会发生一定程度的下落。但当荷载应力水平达到1.0 MPa时，可靠度受累计轴次的增加迅速降低，末期的降低幅度超过50%。