二阶脉冲随机微分方程积分边值问题解的存在性
2021-10-30孙会贤顾海波马丽娜
孙会贤,顾海波,马丽娜
(新疆师范大学 数学科学学院,新疆 乌鲁木齐 830017)
0 引言
积分微分方程通常被用来刻画生物模型、化学动力学、流体力学等现实生活中的很多现象。实际上,用随机微分方程或者随机积分微分方程来描述一些自然现象更为合理[1-5]。另外,在很多动力系统中都会有脉冲现象的存在,所以在考虑随机干扰的同时考虑到脉冲的影响很有必要,脉冲微分方程的特点引起了学者们的关注。近年来,许多学者研究了固定脉冲微分方程的初边值问题[6-9]。2019年,文献[10]研究了二阶非线性积分边值问题
正解的存在唯一性,且存在t0∈[η,1]使得a(t0)>0。
Zhao和Chen[11]研究了二阶脉冲微分方程边值问题
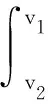
a>0,b≥0,c>0,d≥0,0=t0 解的存在唯一性。 2011年,Xia和Lin[12]讨论了随机微分方程两点边值问题 其中T>0,A和B为d×d阶矩阵,{W(t),0≤t≤T}是k维标准布朗运动,给出了自适应解存在的充要条件,并对于特殊选择的解,得到了边值问题的连续相依性。 2020年,Dong[3]研究了随机分数阶积分微分方程 受此启发,本文将以往所研究的方程的脉冲项和边界条件做了推广,对其限制条件进行了修改,考虑带有脉冲的二阶随机微分方程的积分边值问题 (1) 其中f:J×R×R→R连续,w=(w1,w2,…,wn)T是给定的n维标准布朗运动, 假定(Ω,Γ,P)是一个完备的概率空间,其中Ω是一个样本空间(或任意一个集合),Γ是由Ω的部分子集构成的集合族,Γ中的元素称为事件,P是(Ω,Γ)上的概率,Lq(Ω,Rn)为强可测空间,满足q次可积,且u:Ω→Rn为任意Γt可测d维随机变量。 则PC(J,L2(Ω,Rn))构成一个Banach空间。 则PC1(J,L2(Ω,Rn))构成一个Banach空间。 引理1[13]基本不等式 (ⅰ)p>0,|a+b+c|p≤3p-1(|a|p+|b|p+|c|p); (ⅲ) Doob鞅不等式 定义1 如果u(t)满足: (ⅰ)u(t)是Γt适应的且在(tk,tk+1)处是连续的; (ⅳ) 对于任意给定T∈J,u(t)在t∈[0,T]{tk}上几乎处处满足方程(1),则称u(t)是方程(1)在[0,T]上的解。 引理2(Ascoli-Arzela定理)[14]设S={s(t)}是一个由连续映射s:[a,b]→PC1构成的函数族。若对于任意的t*∈[a,b],集合s(t*)是相对紧的,则S是一致有界且等度连续的,并在S中存在一致收敛函数序列{sn(t)},n=1,2,…,t∈[a,b]。 引理3(Leray-Schauder定理)[14]设PC1为实Banach空间,算子A:PC1→PC1为全连续算子,若集合u∈{u∈PC1|u=λAu,0<λ<1}是有界的,则u=Au至少有一个解。 引理4 设ση2≠2,则边值问题(1)的解u∈PC1(J,L2(Ω,Rn))∩PC2(J′,L2(Ω,Rn))等价于脉冲积分方程 (2) 的解,其中 证明设u是边值问题(1)的解,对式(1)两端积分得 (3) 对式(3)再次积分得 (4) 对式(4)两端进行积分 并对式(4)取t=1,得 结合边值条件可得 将上式代入(4)式得 证毕。 引理5[15]格林函数G(t,s)具有以下性质: (1)G(t,s)在[0,1]×[0,1]上连续; 本节通过运用Leray-Schauder定理讨论了边值问题(1)解的存在性。为了方便,下面将给出所需假设条件及记号说明。本文中,对任意x,y∈R假设如下: (H1)函数f(t,x,y)在J×R×R上连续,函数g(t,x)在J×R上连续。 (H2)存在正常数L,使得|g(t,x)|≤L(1+|x|2)。 (H3)存在有界函数α(t),β(t),γ(t)使得|f(t,x,y)|≤α(t)|x|+β(t)|y|+γ(t)。 (H4)存在非负常数ak,bk,ck,k=1,2,3,…,n,使得 (H5)存在非负常数nk>0,k=1,2,…,n,使得 记 首先定义算子A:PC1→PC1如下 (5) 并对式(5)关于t求导,即 定理1 若假设条件(H1)~(H5)成立,且满足1-F1>0,则边值问题(1)至少存在一个解。 证明定理的证明可分解为以下4个步骤: (1)先证A是一个连续算子,对于任意{un}∈PC1,存在u0∈PC1,使得un→u0(n→∞)。 并且有 当n→∞时,根据f,g,G的连续性可知,E‖(Aun)(t)-(Au0)(t)‖2→0且 E‖(Au′n)(t)-(Au′0)(t)‖2→0。 因此,A在PC1上是一个连续算子。 (2)对任意的u∈PC1,且u(0)=0,则由 可得 则 因此,只需验证E‖(Au′)(t)‖2一致有界即可。并且由(H5)可得,存在Nk>0,k=1,2,…,n,有 从而 其中 因此,结合(H3)可得 (6) (3)对任意的u∈PC1,v1,v2∈(tk,tk+1),当t1 (7) 由(7)式可知,当|t1-t2|→0时,E‖(Au)(t1)-(Au)(t2)‖2→0,对任意的有界集Ω∈PC1,结合(6)(7)式可知,A(Ω),A′(Ω)在每个Jk上等度连续,因此推出A是等度连续的,即A在PC1上是相对紧的。运用引理2(Ascoli-Arzela定理)可知A:PC1→PC1是全连续算子。 (4)对任意u∈{u∈PC1|u=λAu,0<λ<1},对u(t)=λAu(t),其中λ∈(0,1)有 从而有‖u‖=sup|λ(Au)(t)|≤‖(Au)(t)‖≤C,得到u∈{u∈PC1|u=λAu,0<λ<1}是有界的,由引理2、引理3可知,方程(1)的解等价于算子A的不动点,即边值问题(1)至少有一个解,证毕。 考察二阶脉冲随机微分方程 (8) 其中 易知 从而边值问题(8)满足定理1的所有条件,因此边值问题(8)至少存在一个解。
1 预备知识
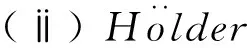
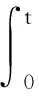
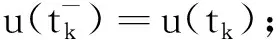
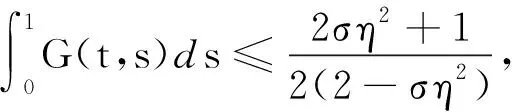
2 主要结果

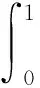


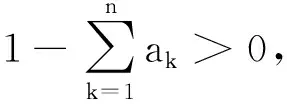
3 应用举例
