基于SERF原子磁强计的三轴磁场顺序补偿方法研究
2021-10-30康翔宇范正焜高秀敏
康翔宇,徐 俊,范正焜,李 阳,高秀敏
(上海理工大学 光电信息与计算机工程学院,上海 200093)
引 言
无自旋交换弛豫(spin exchange relaxation free,SERF)原子磁强计已被证明是世界上灵敏度最高的磁强计之一[1-2],与超导量子干涉仪(SQUID)相比,SERF原子磁强计具有超高灵敏度、体积小、非致冷等特点[3]。由于SERF原子磁强计有极高的灵敏度,因此在空间探测[4]、基础物理研究[5-6]、磁性能检测[7-8]、生物磁学[9-10]等领域得到了广泛的应用。
SERF原子磁强计必须在原子密度高、磁场强度低的SERF区工作。磁场越低,磁强计的灵敏度就越高。在磁场测量时,为了使SERF原子磁强计获得极高的测量灵敏度,通常对其采用被动屏蔽与主动补偿相结合的方式。被动屏蔽只能将空间磁场降到一定的程度[11],为了达到更好的屏蔽效果,普遍采用三轴线圈系统对磁场进行补偿[12]。国内外已有很多的专家和学者提出了SERF磁强计的主动补偿方法。普林斯顿大学的Seltzer等[13]提出了一种交叉调制补偿剩余磁场的方法,可以同时实现三个方向的磁场补偿,但这种方法是从随时间漂移的直流项中提取出来的,在一定程度上是不准确的。威斯康辛大学的Li等[14]利用Z方向磁场的参数调制来抑制与通过烤箱的气流相关的噪声,并使用单探头光束同时检测X方向磁场和Y方向磁场分量,但是在计算调制时使用了近似估计计算,这样调制使得磁强计的灵敏度有所降低。国内北京航空航天大学对于原子磁强计的研究较为深入,Fang等[15]利用SERF原子磁强计本身的某些部分,通过分析原子自旋的动力学特性,实现了对光泵的补偿,但这种方法只适用于较大磁场的补偿。Fang等[16]提出了探针抽运效应的原位磁补偿方法,通过在优化点处对探针光束波长的优化,抑制了对探测灵敏度的依赖,这种方法只能补偿一定范围的剩磁,无法实现大范围磁场补偿。Zhao等[17]提出了一种基于零场共振的非调制补偿方法,通过最大化零场共振信号的一阶微分,实现了沿泵浦方向和探头方向的磁场同步补偿,但这种方法较难实现。
本文基于SERF原子磁强计的基本原理,提出了一种SERF原子磁强计三轴剩磁顺序补偿方法。本文提出的三轴磁场顺序补偿方法更具有普适性,剩磁的补偿范围很大,涵盖了从非SERF态到SERF态的整个过程,采用三角调制与正弦调制的补偿方式使得补偿精度更高,可以将三个方向的磁场补偿到0.1 nT以下。
1 SERF原子磁强计三轴磁场顺序补偿原理
图1为SERF原子磁强计的实验平台简图。实验中SERF原子磁强计泵浦光平行于Z轴,检测光路沿X轴方向,垂直于泵探头平面的方向被定义为Y轴。测试过程中,泵浦光照射到原子气室使原子自旋并保持方向一致,探测光则沿与泵浦光垂直的方向,检测碱金属原子的自旋指向[18],检测信息中包含与磁场相关的参量,进而可以得到磁场信号。

图1 SERF原子磁强计实验平台简图Fig.1 Schematic diagram of the experimental platform of the SERF atomic magnetometer
在自旋进动足够慢的 SERF 体系中,设 ω 为拉莫尔进动频率, RSE为自旋交换率,则存在ω/RSE≪ 1 。基态电子自旋的动力学可以用Bloch方程来描述[19],即
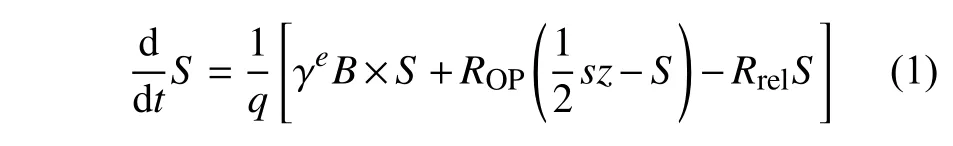
式中: S 为抽运光束的光子极化率,等于圆偏振光的光子极化率; q 为减速因子; γe为电子旋磁比; B 为外加磁场矢量; ROP为光抽运速率; s为电子自旋矢量; Rrel为除了光抽运速率外的所有退偏振速率之和; z 是抽运光的方向。
为了方便计算,引入了无量纲磁场参数 α ,其表达式为

式(6)中, k1、 S0均为正值,X方向的偏导数正比于 αx, αx是与X方向磁场相关的量,而且 αx前面的系数为负值,当X方向磁场等于0时,光电探测器的输出 PZ会存在一个极大值。
同理,从式(7)可以得到,当Y轴方向磁场最小时,光电探测器的输出存在一个极大值。从式(8)可以看出,Z轴方向磁场与X轴方向和Y轴方向不同,其等式前系数为正值,故光电探测器的输出存在一个极小值点,因此当Z轴磁场最小时,光电探测器输出最小值。
根据上述原理,可以确定三个方向磁场的补偿点,从而对磁场进行补偿。
经过了第一步的补偿,此时三个方向的剩磁小于10 nT,在泵浦光与探测光同时作用下,原子磁强计进入SERF态工作。顺序补偿的第二步补偿范围在0.1~10 nT之间,采用在原有剩磁的基础上添加锯齿波的方式对三轴磁场进行补偿,在这里称为三角调制。此时光电探测器位于X方向,探测器的输出正比于 Sx。设置比例系数 k2,光电探测器的输出为 PX,则:
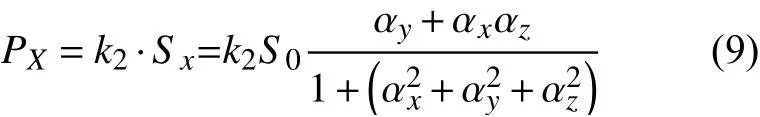
采用三角调制的方法在三个方向原有剩磁的基础上分别添加锯齿波调制磁场,原子磁强计的吸收曲线与色散曲线会呈现出规律性变换。根据光电探测器的输出曲线可以对三轴剩磁进行补偿,调制精度一般会受电流源以及光电探测器的灵敏度的限制,而在0.1~10 nT范围内采用三角调制补偿会更加精确。
经过了三角调制补偿之后,磁场强度小于0.1 nT,顺序补偿的最后一步是通过添加周期性正弦函数来调制磁场,以进一步补偿三维剩磁。光电探测器仍位于X方向,此时磁场已经被补偿到非常小的量级,式(9)可以简化为
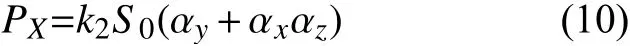
由式(10)可知,在三个方向的磁场参数中, X 方向的剩磁参数和 Z 轴方向的剩磁参数存在耦合关系。再分别对X方向和Z方向添加正弦调制磁场:
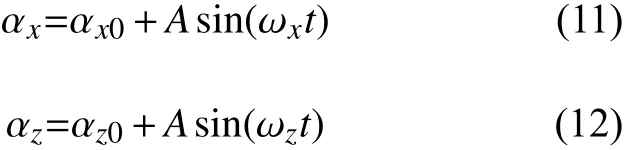
在式(11)和式(12)中, αx0和 αz0表示经过补偿后两个方向的剩磁,A表示调制幅值。由此可以得到在X 方向和Z方向上经正弦调制后的磁场:
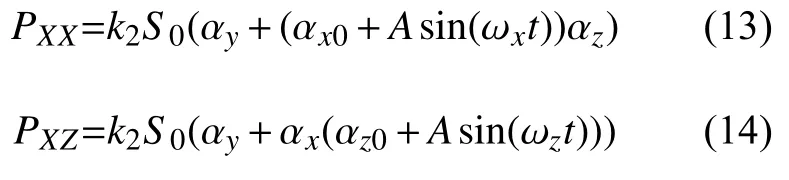
分别添加正弦调制磁场得到式(13)和式(14),正弦调制可以通过调制一个方向的磁场补偿互相耦合的另一个轴向的磁场,通过不断地交叉调制逐步减小两个耦合方向的磁场。
2 SERF原子磁强计顺序补偿方法仿真实验
为了更直观形象地说明磁强计顺序补偿的整个过程,本文给出了补偿过程的仿真。仿真采用的参数如下:
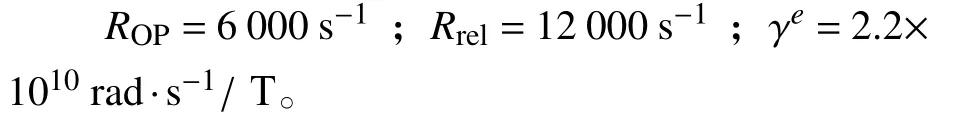
首先仿真顺序补偿过程中的第一步,即仿真只有泵浦光作用时磁场的补偿。设置每个方向的初始磁场,即X、Y、Z三个方向剩磁分别设定为280 nT、180 nT和80 nT。仿真结果如图2、图3、图4所示。
图2是模拟只有泵浦光作用时,X方向的磁场变化过程。在X方向原有剩磁的基础上,添加扫描磁场,光电探测器的输出呈现规律性的变化:在一个扫描周期内,光电探测器的输出先增大后减小,并出现一个极大值点,这个极大值点对应X轴补偿点。同理,在Y方向添加磁场进行扫描,如图3所示,同样出现了光电探测器输出的极大值点,即Y轴剩磁的补偿点。图4是对Z方向添加扫描磁场时探测器的输出变化曲线,图中极小值点对应磁强计Z方向剩磁为零的点,即极小值点对应着实验中要达到的补偿点。上述仿真过程与前文所述原理一致,说明了补偿方法的可行性。
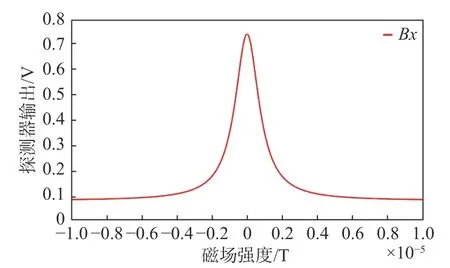
图2 扫描X轴磁场时探测器输出Fig.2 Detector output when scanning X-axis magnetic field

图3 扫描Y轴磁场时探测器输出Fig.3 Detector output when scanning Y-axis magnetic field
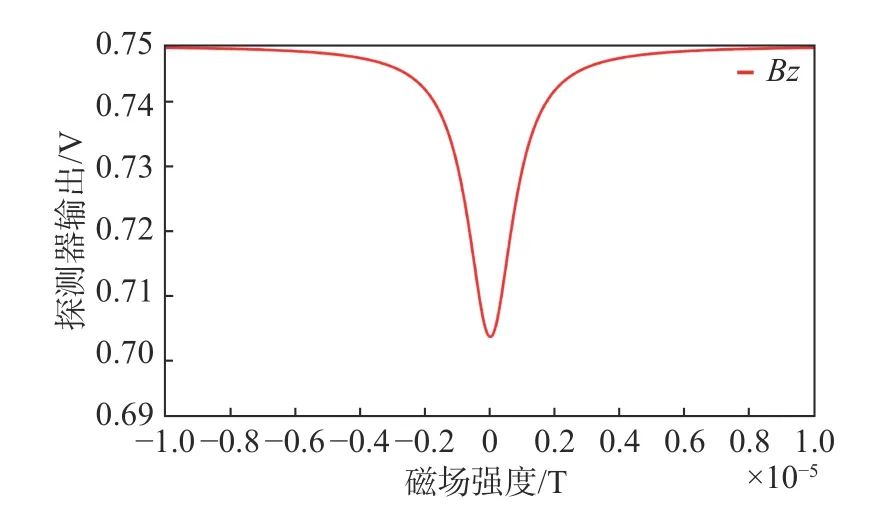
图4 扫描Z轴磁场时探测器输出 Fig.4 Detector output when scanning Z-axis magnetic field
SERF原子磁强计顺序补偿的第二步为三角调制补偿,经过了第一步的补偿之后,三个方向的剩磁均小于10 nT。设置X轴、Y轴、Z轴三个方向的剩磁分别为5 nT、1 nT、5 nT,得到三角调制补偿结果如图5、图6、图7所示。
图5为三角调制过程中调制X方向磁场补偿Z方向剩磁的过程。在X方向剩磁的基础上增添锯齿波调制磁场,选取磁场补偿过程中Z方向上的几个补偿点对比,探测器输出呈现出如下变化:−10 nT时,对应的曲线先减小再增大;10 nT时,对应的曲线先上升后下降;随着剩磁的不断被补偿,曲线逐渐变低。图6中显示的是调制X方向磁场补偿Y方向剩磁的补偿过程。选取同样的特征点,探测器输出在经过零场附近时出现翻转。图7是模拟三角调制补偿过程中调制Z方向磁场补偿X方向剩磁的变化过程,其整体的变化趋势与调制X方向磁场补偿Z方向磁场的变化相同。

图5 三角调制补偿Z轴磁场的过程Fig.5 Triangular modulation compensation process of Z-axis magnetic field
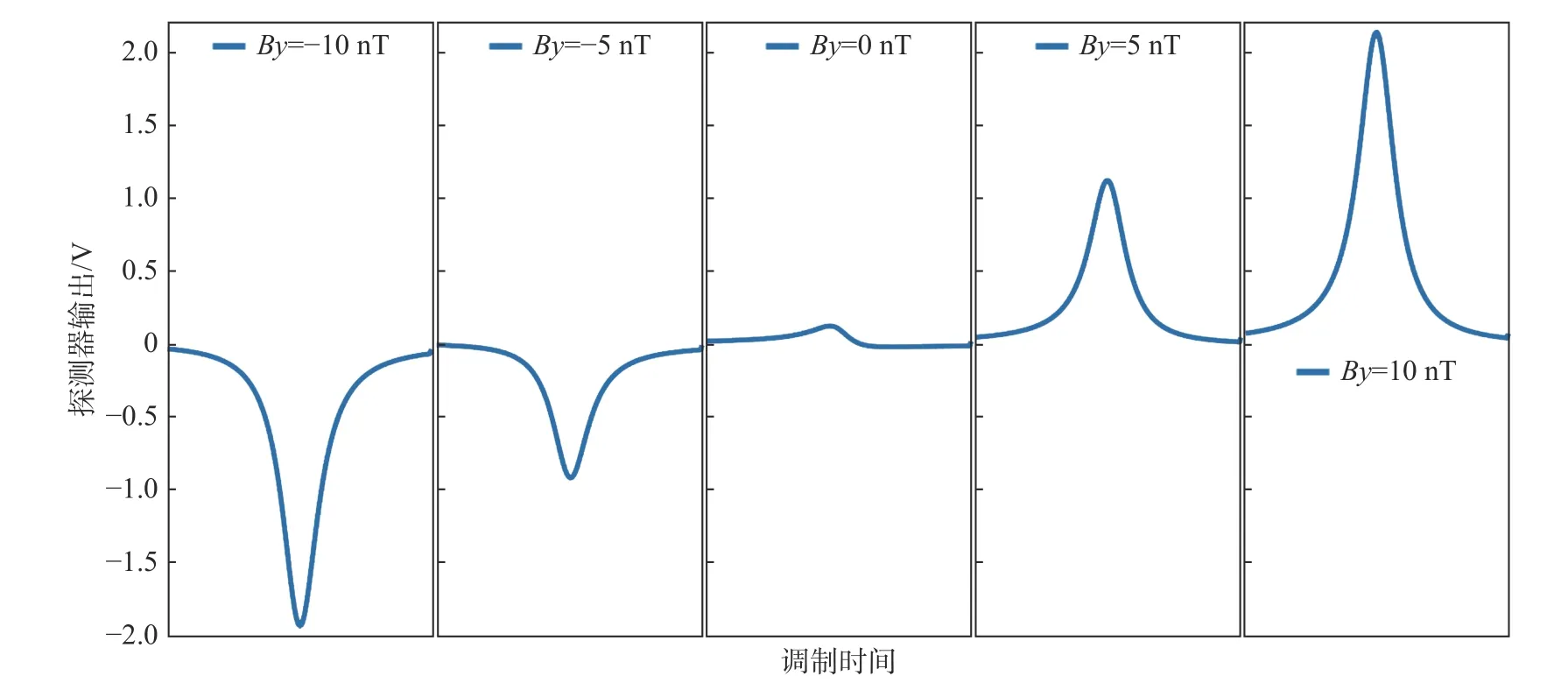
图6 三角调制补偿Y轴磁场的过程Fig.6 Triangular modulation compensation process of Y-axis magnetic field

图7 三角调制补偿X轴磁场的过程Fig.7 Triangular modulation compensation process of X-axis magnetic field
SERF原子磁强计顺序补偿的最后一步为正弦调制。设置X、Y、Z方向磁场分别为0.10 nT、0.05 nT、0.10 nT,正弦调制补偿的仿真结果如图8、图9、图10所示。
图8是模拟了正弦调制过程中对X方向添加正弦调制磁场补偿Z轴磁场时的变化过程,Z方向磁场在归零的过程中,探测器的输出波形的幅值逐渐趋于恒定值,此时探测器的输出值即为实验中要找的补偿点。图9是模拟了调制X方向磁场补偿Y方向上剩磁的过程,在此过程中,探测器的输出形态上一直类似于正弦调制信号的波形,且信号的幅值没有发生变化,仅在输出强度上平移,因此原理上无法对Y方向的磁场进行补偿。图10是调制Z方向磁场补偿X方向剩磁的光电探测器输出变化过程。与图8相同,其输出逐渐趋于稳定值,由此可以确定补偿磁场的参考点。正弦调制的补偿方式又可以称为交叉调制,通过对两个耦合的参数分别添加正弦信号的调制波形来不断减小相对方向的剩磁强度,使磁场逐渐归零。
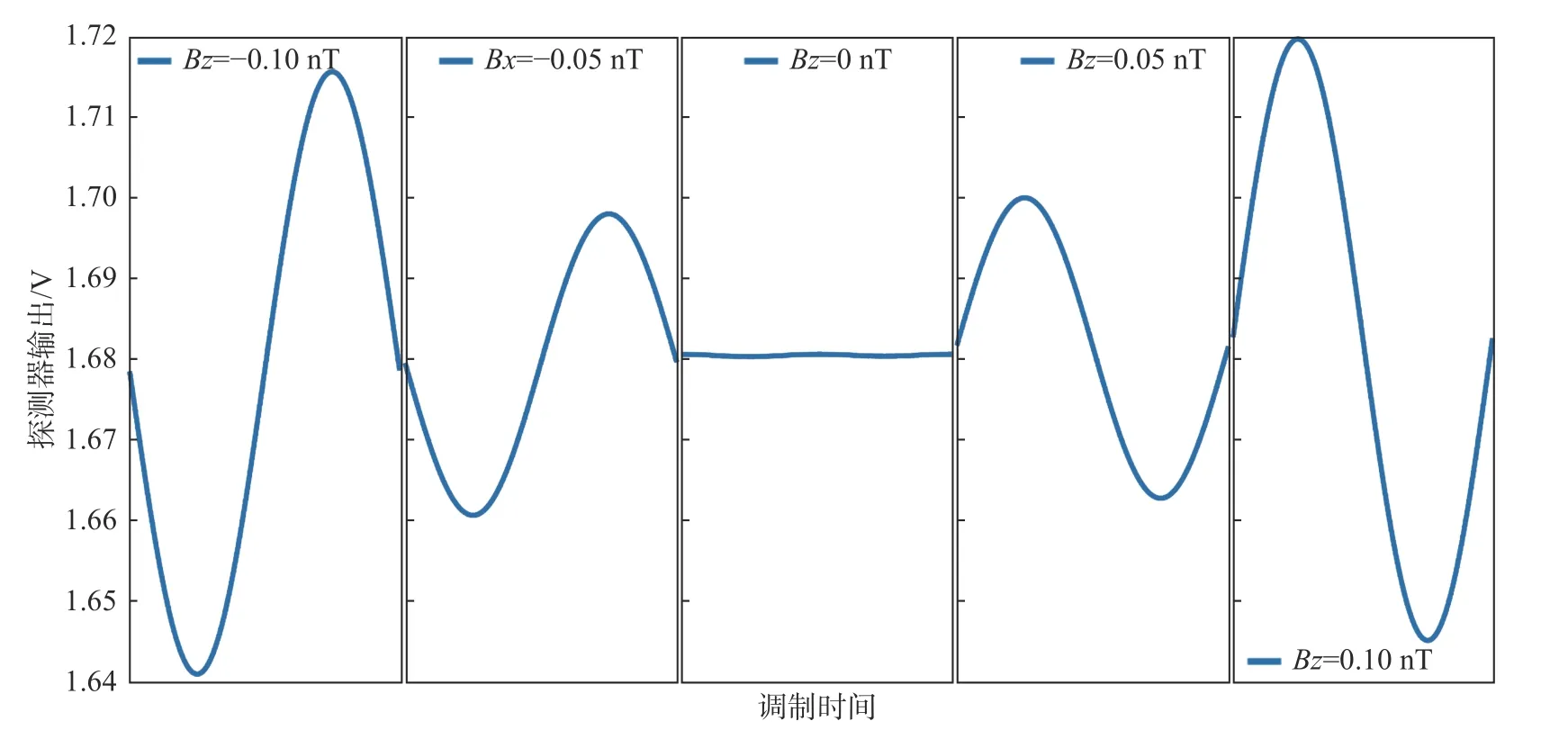
图8 正弦调制补偿Z轴磁场的过程Fig.8 The process of sinusoidal modulation to compensate the Z-axis magnetic field
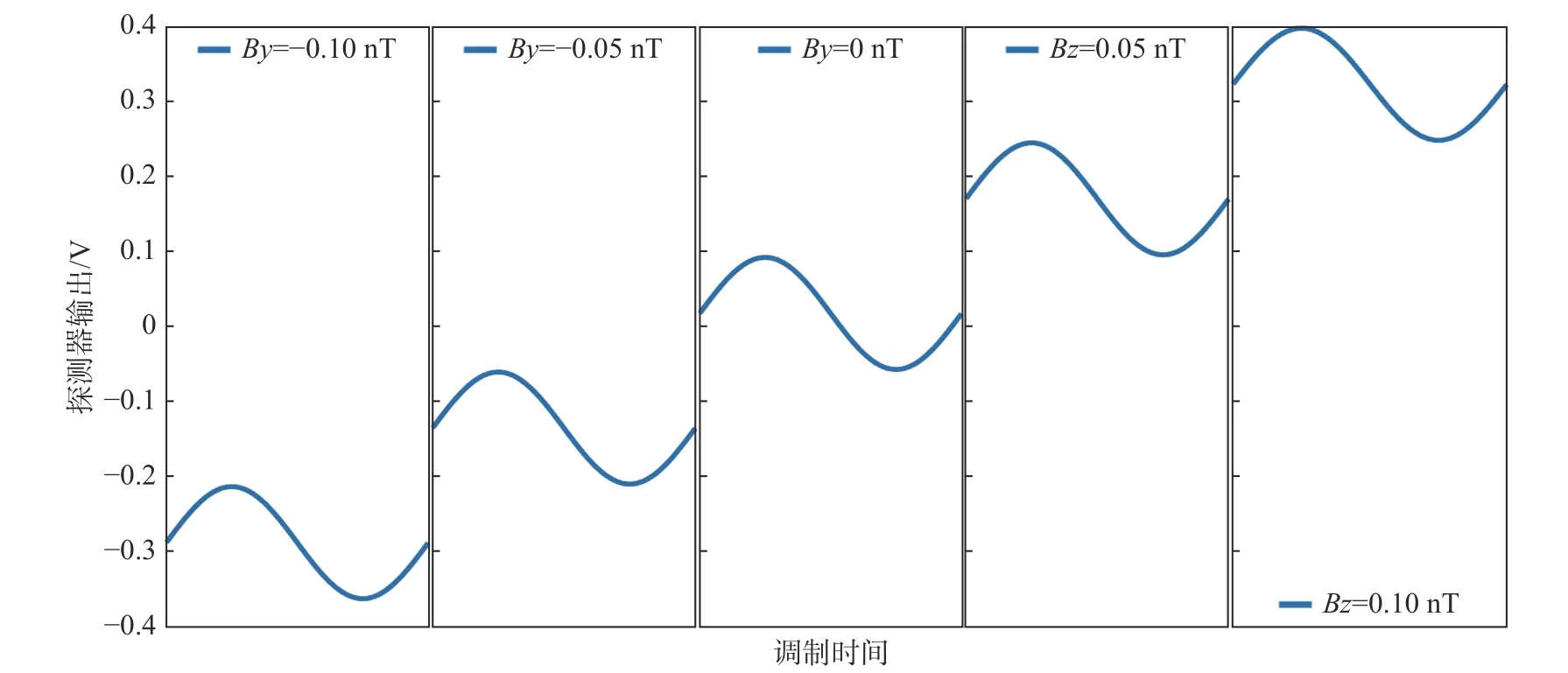
图9 正弦调制补偿Y轴磁场的过程Fig.9 The process of sine modulation to compensate the Y-axis magnetic field
图10 正弦调制补偿X轴磁场的过程Fig.10 The process of sinusoidal modulation to compensate the X-axis magnetic field
3 SERF原子磁强计顺序磁补偿流程设计
上述实验结果验证了SERF原子磁强计三轴方向磁场顺序补偿的可行性。基于上述原理和结果,提出了原子磁强计顺序补偿的具体实施方法,补偿流程如下。
(1)首先只有泵浦光作用时,调节三个方向磁场强度,通过光电探测器的输出变化确定三个轴的补偿方向。
(2)补偿X轴方向与Y轴方向磁场,根据输出是否为极大值判断是否达到补偿点。
(3)补偿Z轴方向磁场,根据输出是否为极小值判断是否达到补偿点。
(4)判断是否达到补偿极限,若已达到补偿极限,则转向下一步骤,否则减小补偿步进量转向步骤(2)。
(5)泵浦光与检测光同时作用,在X轴补偿磁场的基础上添加锯齿波调制磁场,根据探测器的输出信号补偿Z轴磁场。
(6)在X轴添加调制磁场时,采用同样的方式补偿Y轴方向的磁场。
(7)在Z轴补偿磁场的基础上,添加锯齿波调制磁场,根据探测器的输出信号补偿X轴磁场。
(8)在Z轴添加调制磁场时,采用同样的方式补偿Y轴方向的磁场。
(9)判断是否达到补偿极限,如果达到了补偿极限则转向下一步骤,若果没有达到补偿极限则转向步骤(5)。
(10)调制X轴方向磁场,添加正弦调制信号,根据探测器输出补偿Z轴方向剩磁。
(11)调制Z轴方向磁场,添加正弦调制信号,根据探测器输出补偿X轴方向剩磁。
(12)判断是否完成补偿,如果没有完成补偿则转向步骤(10),如果完成补偿则停止主动补偿。
4 结 论
本文提出了一种SERF原子磁强计三轴磁场顺序补偿控制方法,通过MATLAB仿真实验验证了顺序补偿方法的有效性,并提出了具体的补偿步骤。本文提出的方法更适合实际实验条件下的剩磁补偿,特别是在初始剩磁无法确定的情况下,具有普适性。本文方法涵盖的剩磁补偿范围广,包括了原子磁强计的非SERF态和SERF态整个过程。采用三角调制与正弦调制的补偿方式使得补偿精度更高,可以将三个方向的磁场补偿到0.1 nT以下,本文所提出的补偿方法可为原子磁强计磁补偿的进一步研究提供参考。
