振动效应受锚边坡锚固长度优化研究
2021-10-29吕金昕
吕金昕
(四川开放大学, 四川 成都 610073)
1 矿山边坡稳定性分析
露天矿山的边坡稳定性受到不同内外因素影响,经归纳整理,可确定地质因素、自然因素、人为因素为影响露天矿山边坡稳定性的最主要因素。
1.1 地质因素
矿山开采行为需在现有岩层中进行,继而导致矿山边坡条件在矿山边坡稳定性研究中的唯一性,在开挖过程中,采矿平台空间逐渐变化,因此矿山边坡始终处于动态变化状态。矿山边坡由台阶坡面、清扫平台、安全平台、运输平台构成,且各组成部分的数据均受开采情况影响而不断变化,使矿山边坡结构更加复杂多变,而矿山边坡稳定性代表着矿山边坡岩体的允许变形效果,爆破开采等活动产生振动效应时将产生不同效果。
地质因素是决定矿山边坡稳定性的首要因素,矿山构造是有地壳活动变位及变形产生的形态,如断层、节理、褶皱等,而此类地质构造形态决定了矿山边坡岩体的层、缝、面结构特性,当矿山边坡受到爆破开挖振动效应影响而产生滑坡、坍塌时,主要因为矿山岩体结构面抗剪性、抗压性相对较低,且矿山岩体结构面中存在大量柔弱次生矿物,在地下水、降水等因素的综合作用下,进一步降低了矿山岩体结构面抗剪强度,导致滑坡、坍塌等边坡事故发生几率增大,除此之外,矿山地质构造可决定边坡滑体破坏类型,对矿山边坡稳定性产生影响。
1.2 自然因素
影响矿山边坡稳定性的自然因素主要包括地下水、降雨与地震,其中地下水具有溶蚀效果,可逐渐侵蚀矿山边坡岩体内部构造,降低矿山边坡岩体抗剪性、抗压性等物理性质,损坏矿山边坡稳定性;降雨可在矿山边坡平面及坡面造成冲刷效果,形成面流,由于矿山边坡地质构造存在断层、节理、褶皱等形态,进一步扩大了降雨冲刷效果,泥化、软化矿山边坡岩体,降低矿山边坡岩体抗剪性、抗压性,降低矿山边坡稳定性;地震对矿山边坡的影响无法控制,但在地震力反复振动冲击下,使边坡内部岩体产生变形、移位等现象,造成无法预测的破坏效果,对边坡稳定性影响极大。在各类自然因素下,地震对矿山边坡结构的影响较大,在地震反复振动下且由地震引发的惯性力对边坡内部结构损坏较大,地震作用力计算公式如下:

式(1)中,Fi为第i块岩体的水平地震作用力(kN);a为地震加速度(m/s2);x为折减系数,取值0.25;bi为第i块岩体的动态分布系数,取值为1;Wi为第i块岩体的重量(kN);g为重力加速度,取值9.81m/s2。
1.3 人为因素
人为因素主要指矿山开挖活动造成的振动效应,如爆破开挖,在长期开采过程中导致矿山边坡陡峭,若未结合边坡稳定性进行良好规划,会导致开挖活动破坏边坡自身稳定性结构。爆破开挖作为矿山作业最常用开采工艺,边坡将受到爆破开挖造成的强烈振动效应,边坡受到频繁扰动导致岩体构造面规模逐渐增大,对矿山边坡稳定性造成影响,而爆破开挖振动效应对边坡的破坏程度取决于岩体振动速度,因此常采用锚固措施加固矿山边坡来降低振动速度,提升边坡安全性。边坡岩体受到的水平爆破振动力计算公式如下:

式(2)中,Fi为第i块岩体的水平爆破振动力(kN);ai为第i块岩体水平爆破振动加速度(m/s2);bi为第i块岩体爆破振动系数,取值多为0.1~0.3;Wi为第i块岩体重量(kN);g为重力加速度,取值9.81m/s2。
式(3)中,Vi为第i块岩体重量(kN);Q为爆破装药量(kg);Ri为爆破区几何中心至边坡的距离(m);K、a为岩体性质、地质条件、爆破条件等系数,需经振动监测获得详细数据,根据《中国地震动参数区划图(GB18306-2001)》来看,露天矿山抗震设防烈度为8度,地震加速度为0.2g,即a=1.352[1]。
式(4)中,ai为第i块岩体水平爆破振动加速度(m/s2);f为爆破振动频率(Hz);Vi为第i块岩体重量(kN)。
2 基于边坡介质的振动效应分析
锚固技术具有施工便捷、主动加固、承载力大的优势,将锚固技术应用到矿山边坡中可极大提升岩体结构稳定性,现阶段在露天矿山开采中已实现了大规模应用,经工程实践验证发现,锚杆加固在露天矿山爆破开挖振动效应下经常遭受破坏,而损坏的主要原因在于锚固力损失或锚固长度不足而引发剪切脱粘损坏,但在当前受锚边坡工程研究中,锚固参数的设定均建立在实际矿山开采工程经验基础上,基于矿山受锚边坡静载条件获得极限平衡方程,以此完成受锚边坡锚固参数确定工作,但在确定受锚边坡锚固参数过程中,并未结合矿山边坡岩石地质爆破振动效应展开分析,导致锚固效果极大减弱[2]。
结合上述分析可知,矿山边坡稳定性主要受地质因素(岩体结构)、自然因素(降雨、地下水及地震)、人为因素(爆破开挖振动)等因素的影响,其中爆破振动作为矿山主要开采方式,爆破过程短,破坏程度较大,一旦对受锚边坡锚杆造成影响将难以修复。在矿山爆破开采中,由于振动效应将从坡底向上传递给岩体结构层,因此应将坡底振动荷载放在首位,综合考虑其对受锚边坡的稳定性干扰。当爆破振动效应信号传递到受锚边坡时,受到自由面阻挡而产生反射效果,此时受锚边坡岩体结构将受到加速度及变形力影响,受锚边坡岩体结构将跟随振动信号产生位移与突变,干扰受锚边坡稳定性。
为提升锚杆锚固效果,优化锚杆支护长度,应进一步分析爆破振动波在受锚边坡中的传递特点及自由面振动反射效果,本次研究基于均质土坡展开,设定矿山受锚边坡土体为连续弹性介质,在该土体条件下,振动纵波(P波)的传播速度远超于振动横波,振动横波对受锚边坡的影响较小,因此本次优化受锚边坡锚固长度暂不考虑振动横波。当爆破产生的振动波进入边坡界限时,振动纵波(P波)将从坡底入射至边坡坡面,并产生反射效果。具体如图1所示:
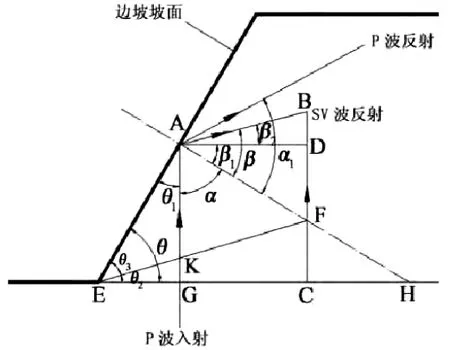
图1 振动纵波(P波)入射传播模型
图1中AH线为振动P波传播至边坡坡面点的法线方向,垂直于切线方向,θ为受锚边坡角度,当振动P波从坡底向上传播至边坡坡面时,受锚边坡角度θ与α角度相等,根据光的折射定律(Snell定律)可得,振动P波入射角、反射角的关系如下:
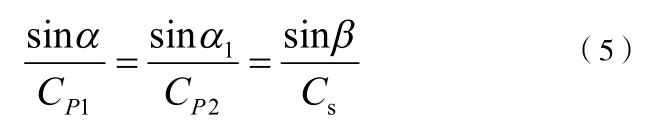
式(5)中,α为振动P波入射角;α1为动P波反射角;β为经边坡坡面反射的SV波反射角;CP1为振动P波入射波速;CP2为振动P波反射波速;CS为经边坡坡面反射的SV波传播波速,由于本次研究所设环境为均质土坡,因此在式(5)中存在以下关系:α=α1,CP1=CP2。
根据图1振动纵波(P波)入射传播模型可知,经边坡面EA反射后的振动P波与SV波反射角存在一定关系,即α1>β,因此,当边坡坡体反射出SV波后,SV波将与振动P波于边坡内部产生干涉叠加,同时SV波对边坡岩体结构介质的振动影响大于振动P波,为更好地研究受锚得边坡锚固长度,从入射振动P波、反射SV波两个方面研究其对边坡的影响范围,及锚杆轴应力、剪切带的变化特征。观察图1振动纵波(P波)入射传播模型还可得出以下几何关系:

结合波的叠加原理,振动波进入受锚边坡坡底后形成入射振动P波波程,即CB段,进入边坡后反射为SV波波程,即AB段,入射振动P波波程、SV波波程产生干涉现象,根据该干涉现象完成振动波对边坡的影响范围研究,此时入射振动P波、反射SV波的产生波程差,通过以下公式进行计算:

式(8)中,λ为波长,k为(0、1、…)等常数。根据波的叠加原理,两个初相位相同的相干波在介质中叠加时,波程差等于零或等于波长整数倍的各点合成振幅最大,即由边坡C点入射的振动P波与坡面反射SV波相遇时的波程差为零或整数时,所产生的振动效果覆盖范围最大。同时结合受锚边坡几何性质及坡体内部振动波干涉叠加来看,在传播模型中所产生的坡表影响范围可波程差可取1倍波长λ,在锚杆支护受锚边坡中,应在锚固规范基础上严格控制锚杆长度,拟设定锚杆长度等于振动纵波长度得,结合式(8)得出边坡坡面垂直方向干涉叠加造成的振动增强最大影响深度。


图2 边坡角度θ与最大影响深度AF间的关系曲线
图2为边坡角度θ与最大影响深度间的关系曲线,由图2可知,与边坡表面垂直的最大影响深度AF与边坡角度θ存在良好关联,两者存在正相关关系,最大影响深度随边坡坡度的增加而提高,此时边坡坡度与振动波长间的存在1.15~2.5的倍数关系,因此可根据图2相关性特征关系曲线及边坡坡角,得出锚杆支护在边坡抗振设计中的长度数值,经计算后得出锚杆长度应大于1.15~2.5倍的振动波长,以此满足受锚边坡抗振强度性能要求,同时锚杆长度应大于边坡最大影响深度[4]。
3 振动效应受锚边坡锚固长度优化核验的工程实例分析
为提升本次优化研究针对性及有效性,了解振动效应下的受锚边坡锚固长度最佳值,本次选取某露天矿山边坡展开工程实例研究,该露天矿山边坡土质与上述设定条件一致,坡岩土介质为弹塑性土体,以此为工程实例具有较好的验证效果。
3.1 工程概况
为进一步验算在受锚边坡中振动效应的最大影响深度及上述锚杆长度优化数值有效性,选取某露天矿山边坡开采工程展开实例研究,该露天矿山边坡岩土介质为弹塑性土体,边坡弹塑性土体密度为1850kg·m-3,内聚力为32kPa,内摩擦角为12°,弹性模量为11GPa,泊松比为0.33,阻尼系数为125000kN·s·m-1。根据Mohr-Coulomb强度准则展开分析,该露天矿山边坡坡度为35°,高度为30m,一级安全等级,根据锚固计划进行边坡加固,拟设置6排预应力锚杆,加强边坡稳定性。为确保速度计算有效性,运用动力时程逐渐输入振动荷载,由于该露天矿山边坡结构较为简单,采用瑞利阻尼进行锚固,调整速度谱,使频率范围可实现主要动力能量的全面覆盖,并展开动力计算,此时可获得中间频率,在本次研究分析中,中间频率fmid为1Hz,将防烈度设定为8级,振动波加速度最大值amax为0.2g,加载振动荷载振动时间为5s,振动荷载作用的速度时程如图3所示。
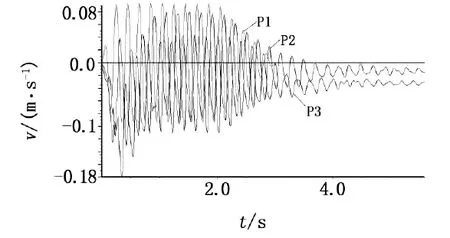
图3 振动荷载作用的速度时程
3.2 参数验证
结合该露天矿山边坡土体参数及条件,从添加振动负荷及不添加振动负荷两种情况展开分析。运用有限差分程序进行边坡锚固结构剪应变率计算,并判断出锚杆轴力的分布特点。若为添加振动负荷,在本次实例验证中,锚杆长度为12m,在有限差分程序应用下计算出受锚边坡锚杆轴力分布及边坡剪应变率,在该露天矿山边坡结构中,振动波由边坡坡底出现,逐渐在边坡内部结构中形成从坡底至坡顶的贯通剪切带,运用12m锚杆锚固加固后,该贯通剪切带范围得以缩小,该露天矿山边坡结构逐渐趋于稳定,在此过程中锚杆轴力呈现为单驼峰特征,且该锚杆轴力前段较大,沿锚固方向逐渐降低。若添加振动负荷,则锚杆轴力及振动效应剪应变率将发生改变,由于受锚边坡所承受的荷载提升,因此受锚边坡剪切带范逐渐增大,根据实例检测发现,在考虑振动负荷情况下,锚固段长度增加至2m,在此情况下边坡形成贯通剪切带,且情况较为严重,边坡存在失稳隐患,此时根据干涉叠加原理最大影响深度及振动荷载波长特征进行解析,将锚杆长度延长至14m,为原锚杆长度的116.7%[5]。将14m长度的锚杆应用到露天矿山边坡加固中,发现剪应变率有所降低,边坡剪切带涉及范围进一步缩小,由于锚固效果提升,在此次实例验证中并未出现危害性较大的贯通剪切带,同时锚杆杆体受力情况有所改善,呈均匀受力状态,锚杆在振动效应下不易损坏,锚固效果较好,极大提升了露天矿山受锚边坡稳定性。随着能源需求量的提升,露天矿山边坡稳定性成为行业重点研究对象,为增强边坡稳定性,降低振动效应对边坡结构的影响,应结合矿山实际情况判断锚杆长度,降低振动效应剪应变率,均衡锚杆受力分布。
4 结束语
综上所述,矿山边坡稳定性的影响因素主要包括地质因素、自然因素、人为因素,在本次研究中重点分析爆破振动对矿山边坡的影响,结合振动效应传播特点构建传播模型,得出深度解析式,结合某露天边坡矿山展开实例分析,对计算结果进行核验,当锚杆长度达到14m时,露天矿山边坡剪切带范围有所缩减,此时锚杆受力均匀,锚固效果得以增强。
