具有时变时滞的复值神经网络的概周期解

方聪娜，宾红华

(集美大学理学院，福建 厦门 361021)

1 预备知识

神经网络是一门迅速发展的交叉学科，它广泛应用于大规模集成电路、人工智能、信号处理、神经生理学、图像识别等领域.在过去的几十年，许多学者研究了各类实值神经网络模型的动力学行为，并且取得了丰富的研究成果[1-7].但是，在诸多应用领域中实值神经网络有一定的局限性，如在电子信息工程领域，人们需要处理复数数据，因此，作为实值神经网络的推广，复值神经网络自然而然地被提出来，而且解决了一些实值神经网络不能解决的问题[8]，成为了一个新的研究热点.这些年，一些学者主要研究了复值神经网络的平衡点或周期解的存在性、稳定性、耗散性等问题[9-13].

我们知道，非自治神经网络的概周期振荡是很重要的一种动力学现象，概周期解也比周期解更具有一般性，但对复值神经网络概周期解的相关问题的研究却寥寥无几，所以，研究复值神经网络的概周期解具有一定的理论意义和实用价值.另一方 面，从现有文献来看，在研究实值神经网络或复值神经网络时往往要求神经元激活函数满足全局Lipschitz条件，显然这一条件过于苛刻，限制了一些结论的应用.

基于上述研究，本文研究了下列具有时变时滞的复值神经网络

j=1,2,…，n

(1)

的概周期解问题，其中zj(t)∈C表示第j个神经元在t时刻的状态；dj(t)>0表示自反馈连接权重；ajk(t)∈C和bjk(t)∈C表示神经元之间的连接权重；Ij(t)∈C表示第j个神经元在t时刻的外部输入；fk∈C和gk∈C表示神经元激活函数；τjk(t)表示传输时滞且满足0≤τjk(t)≤τ(τ>0为常数).本文在不要求神经元激活函数满足全局Lipschitz条件的情况下，利用Banach空间中的不动点定理及指数型二分性，建立了保证系统(1)存在唯一的一致稳定的概周期解的充分条件，同时也给出了其概周期解的存在范围，这些结果都是新的.

2 相关引理

定义1对于复值函数z(t)=zR(t)+izI(t)(zR(t)=Re(z(t)),zI(t)=Im(z(t)))，若zR(t),zI(t)都是概周期函数，则称z(t)为概周期函数.

考虑如下概周期实值系统

x′(t)=A(t)x(t),

(2)

和

x′(t)=A(t)x(t)+k(t),

(3)

这里A(t)是t的概周期矩阵函数，k(t)是t的概周期向量函数.

定义2[14-15]如果存在投影P和正常数K,α,β使得系统(2)的基本解矩阵X(t)满足

‖X(t)PX-1(s)‖≤Ke-α(t-s),(t≥s),

‖X(t)(I-P)X-1(s)‖≤Ke-β(s-t),(s≥t),

则称系统(2)在R上满足指数型二分性.

引理1[14-15]若系统(2)满足指数型二分性，则系统(3)存在唯一的概周期解，它可表示为

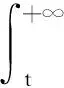
对于复值神经网络(1)，做如下假设：

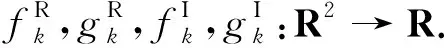
由假设1)和2)，系统(1)可化为如下实值系统

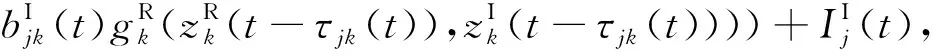
j=1,2,…,n,

(4)

因此，对复值神经网络(1)的概周期解的研究可转化为对实值神经网络(4)的概周期解的研究.

系统(4)的初始条件为

t0≥0,j=1,2,…,n,

‖Z(t)-Y(t)‖<ε,(t≥t0),

3 主要结果

对于实值神经网络(4)，做如下假设：

这里v∈{R,I},k=1,2,…,n.

j=1,2,…,n,

j=1,2,…,n,

j,k=1,2,…,n,

j=1,2,…,n,

j=1,2,…,n,

j=1,2,…,n.

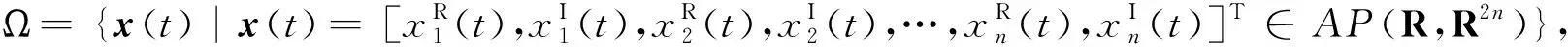
(5)

由条件(i)及引理1，引理2可知系统(5)存在唯一的概周期解

其中

(6)

因为Zφ(t)∈Ω，所以现在可定义映射Φ:Ω*→Ω为Φφ=Zφ,下面证明Zφ(t)∈Ω*.

由式(6)及条件(ii)(iii)可得

类似于上述的计算可得

下面我们证明映射Φ：Ω*→Ω*是一个压缩映射.对任意的φ,φ∈Ω*,设

则

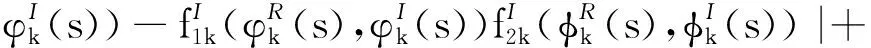
最后证明系统(4)的概周期解Z(t)是一致稳定的.

j=1,2,…,n,

(7)

j=1,2,…,n,

j=1,2,…,n.

(8)

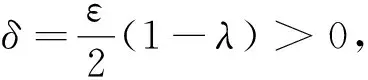
‖Z(t)-Y(t)‖<ε,(t≥t0)，

(9)

若不然，则一定存在t1>t0使得

‖Z(t)-Y(t)‖<ε,(t0

(10)

且

‖Z(t1)-Y(t1)‖=ε.

(11)

此时可由式(7)、(8)、(10)、(11)得

(1+λ)ε/2<ε,

这个矛盾说明了式(9)是成立的，故系统(4)的概周期解Z(t)是一致稳定的.定理1证毕.

4 应用举例

考虑如下具有时变时滞的复值神经网络

(12)

其中

b12(t)=0.4sint+i0.2cost,

τ22(t)=|sin(5t)|/4,

计算可得