基于无人机多光谱点云数据与MGGP人工智能算法的水质探测方法研究

敖瑞贵，闫晓惠，许士国

(大连理工大学，辽宁 大连 116024)

水质探测是水生态环境保护工作中的重要环节，但传统的野外采样或传感器监测等方法具有观测范围小、人力物力成本高等缺点。遥感技术具有观测范围广、数据获取速度快和成本低等优点，已经成为传统水质调查方法的有力补充，而近年来发展起来的无人机航测技术可以提供更高的时间与空间分辨率且受水汽的影响较小，因此有望进一步提高水质参数的调查效率。之前的学者已尝试采用无人机多光谱影像对小微水域的总磷、悬浮物浓度、浊度等水质参数进行反演，证明了该方法在小微水域水质调查中的可行性。但是，无人机飞行高度受限，无法直接获取整个大面积水域的完整正射影响，而为了获得较好的拼接质量，需要确保无人机飞行的航向重叠度和旁向重叠度，增加了无人机的操控难度。此外，无人机在航测过程中也易受风速等影响而发生倾斜，进一步增大图像的拼接难度。因此，目前的无人机多光谱技术尚难以应用于较大水域的水质探测中。

鉴于此，本文以悬浮物浓度为例，提出并测试一种基于无人机多光谱点云数据和MGGP人工智能算法的水质探测方法。首先利用无人机搭载多光谱相机在研究区域上空获取大量的多光谱数据，得到悬浮物浓度的点云数据，再分别利用传统的克里金空间插值法和MGGP人工智能方法得到验证点的悬浮物浓度值。结果表明，基于无人机多光谱点云数据和MGGP人工智能算法的方法可有效解决大面积水域的水质探测问题，为水质参数的调查提供新的技术手段。

1 研究方法

1.1 无人机多光谱数据获取与处理

研究区域面积约为76372m2，周长约为1109m。本研究采用的无人机为大疆悟Inspire 2，搭载Mica Sense Red Edge多光谱传感器获取数据。于2021年5月27日进行无人机航拍作业，得到140组带有GPS定位的多光谱影像，每一组有Blue(0.450～0.515μm)、Green(0.525～0.605μm)、Red(0.630～0.690μm)、Red edge position(0.670～0.760μm)、NIR(0.770～0.890μm)5个光谱带的数据。根据已有的研究成果，应用红光波段与近红外波段之和与绿光波段的比值作为光谱参数，即公式(1)。

(1)

式中，V—用于反演模型的光谱参数；R2、R3、R5—分别为绿光波段、红光波段和近红外波段的光谱反射率数据。

对所有的多光谱影像进行辐射校正和辐射定标，在MATLAB软件中得到每个像元的地物反射率数据，由反射率得到光谱参数，经过数据质量检测，应用已有的悬浮物浓度模型(公式2)得到140个位置点的悬浮物浓度点云数据。点云数据的空间位置采取随机布设方式以降低其有序性，可更好地验证MGGP方法的性能，具体的位置点如图1所示。将点云数据随机划分为两组，其中112组数据(约80%)用于模型训练，而剩余的数据则假设为未见数据以用于算法验证。

图1 点云数据位置分布图

本文的研究目的是提出并测试无人机多光谱点云数据结合MGGP方法的可行性而非测试已有悬浮物浓度模型的精确度。模型参数对浓度绝对值略有影响，但基本不改变浓度的空间分布规律。因此，在后续的分析中，将模型的计算值假定为实际值，用于测试MGGP方法的水质参数估算性能。

y=-2582x2-2408x+7473

(2)

式中，y—悬浮物浓度， mg/L；x—光谱参数。

1.2 传统空间插值法

传统空间插值法选取克里金空间插值法，利用训练组的112组点云数据进行空间插值，得到验证点位置的预测值，与真实值比较，分析克里金法的可行性。克里金法以变异函数理论与结构分析为基础，在区域化变量间存在空间自相关性的前提下，根据未知点和其周围影响范围内样本点的距离及空间关系拟合模型确定权重，对未知点的取值进行无偏最优估计。该方法的计算公式为：

(3)

式中，z(x)—未知点的预测值；z(xi)—样本点处悬浮物浓度值；λi—权重；n—样本数。

1.3 MGGP人工智能算法

多基因遗传规划(MGGP)是遗传规划(GP)的发展，结合了GP的模型构建能力和统计回归方法的参数估计能力，能够通过一系列过程找到输入和输出变量之间的关系。在传统的遗传规划中，进化模型由单棵树组成，而在多基因遗传规划中，每一个回归模型都是多棵树的加权线性组合。其工作流程可以概括为：随机产生初代种群，包含一组由函数和变量组成的个体；计算种群中每个个体的适应度；选择适应度好的优良个体为母体；通过突变、交叉、复制等方式产生新的个体，创造新的一代(子代)；重复第二步和第三步，直到满足终止准则。

1.4 评测指标

采用均方根差(RMSE)和R2值来量化方法的精准度，其中R2越接近1、RMSE越小则表示预测值与实测值误差越小。公式分别为：

(4)

(5)

式中，y—预测值；x—实际值：N—验证点的个数。

2 结果与讨论

2.1 悬浮物浓度数据统计特征

无人机多光谱的典型影像如图2所示，对每个目标范围，多光谱相机拍摄5通道影像，通过辐射校正和辐射定标后得到光谱反射率，再通过悬浮物浓度反演公式得到每个点的悬浮物浓度。本水域的悬浮物浓度平均值为8.97mg/L，处于较低水平。最小值为0.45mg/L、最大值为16.16mg/L、中间值为9.05mg/L、标准差为4.09mg/L、方差为16.73(mg/L)2、峰态系数为2.13、偏态系数为-0.12。

图2 水面多光谱影像

2.2 基于传统空间插值法的悬浮物浓度估算

利用筛选出的112个样本点(训练组)、采用Arc GIS的克里金法进行空间插值，估算了28个验证点(验证组)位置的悬浮物浓度值。如图3所示为克里金法估算值与实际值的对比图，其中横坐标为实际值，纵坐标为克里金估算值，中间线为1∶1等值线。当各散点位于等值线上时，表明估算值完全等于实际值；当散点位于等值线的左上侧时，表明该方法高估了实际值；当散点位于等值线的右下方时，表明该方法偏向于低估实际值。由图3可知，各散点较为均匀地分布于等值线的两侧，且偏离较小，因此预测值与实际值相差不大。经计算，R2值为0.936，RMSE为1.338mg/L，其中R2值较高而RMSE值较低，则证明了该方法具有一定的可行性。

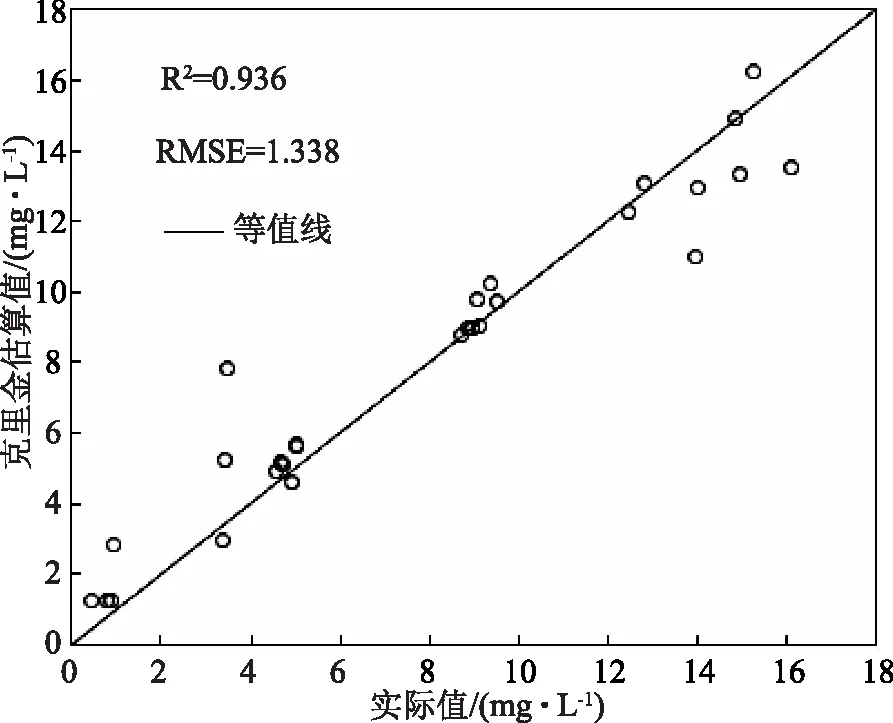
图3 基于克里金空间插值法的实际值与估算值

2.3 基于MGGP算法的悬浮物浓度估算

采用与克里金法一致的112个样本点云数据作为训练数据。MGGP模型的训练演化过程如图4(a)所示，其中横坐标为进化代数，每代产生500个模型，横坐标代表模型的RMSE值。在进化初期，MGGP算法随机产生数学模型，其误差较大，但经过复制、突变、交叉等算法处理，模型的误差迅速下降，在第10代左右模型种群的误差值变化幅度即已较小，运行更多的进化代数不再显著提高种群的精确度，因此将最终的总进化代数设置为100即可满足要求。图4(b)对比了悬浮物浓度的实际值与MGGP预测值。由图可知，相比于克里金空间插值方法，MGGP预测数据与实际数据更加接近。其验证数据集的R2值为0.964，高于克里金法的0.936，说明MGGP方法可更为准确地判断数据的升降变化规律。RMSE值为0.926mg/L，低于克里金法的1.338mg/L，因此在本案例中，MGGP法可将传统空间插值法的误差降低约30%。克里金方法已经预设了基本的模型结构(公式3)，而该结构未必精确。MGGP算法则可排除人为预设模型结构的误差且可深度挖掘变量之间的相互影响关系，因此MGGP方法的估算结果更为准确。综上，基于无人机多光谱点云数据结合MGGP人工智能算法的水质探测方法具有较好的可行性。

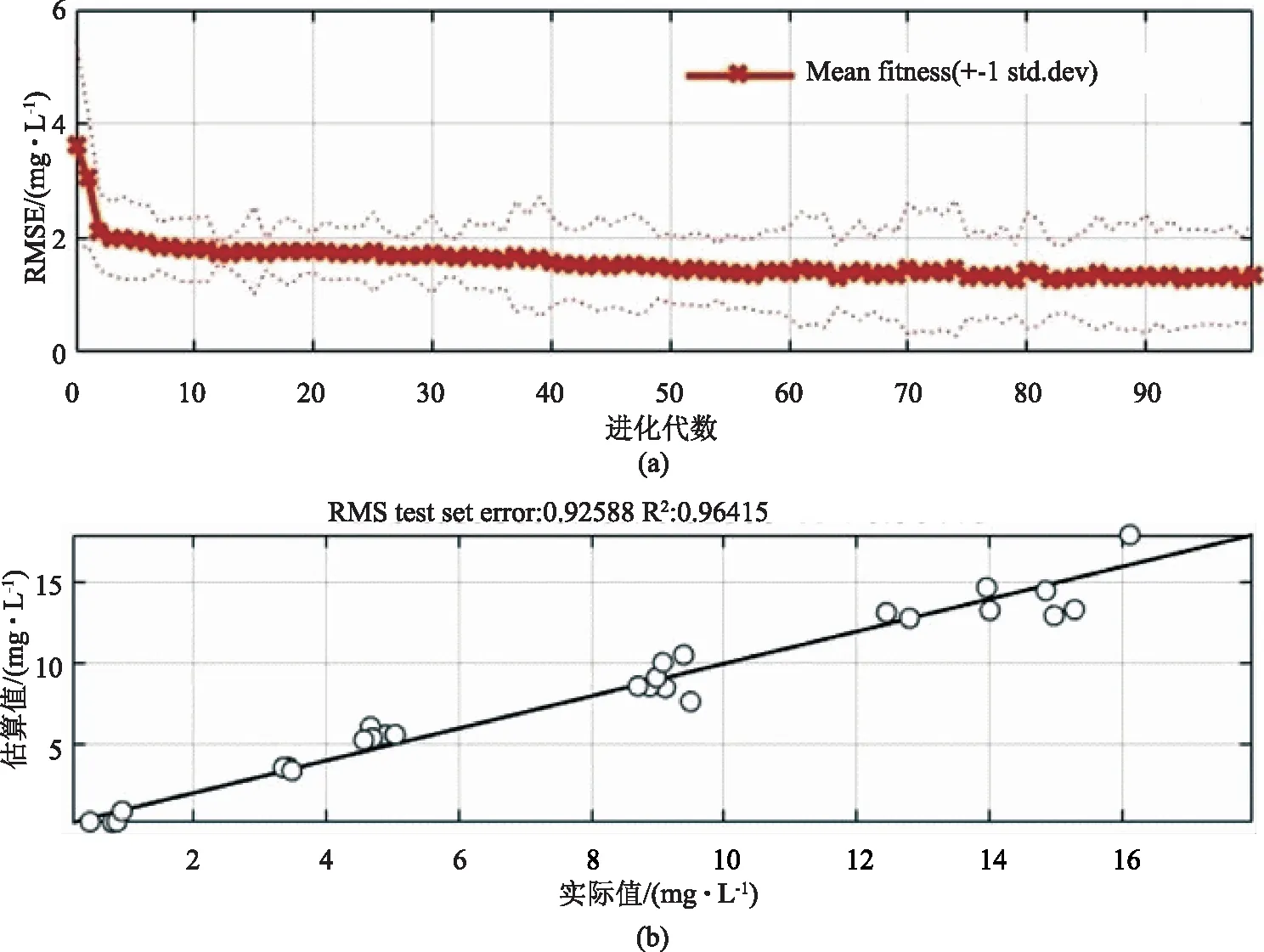
图4 基于MGGP的实际值与预测值

3 结论

本文提出了基于无人机多光谱与MGGP人工智能算法的水质参数探测方法。结果证明，采用该方法估算研究范围内未知点的水质参数是可行的。估算值与实际值之间的误差很小，且相比传统的克里金空间插值法， 该方法的R2值从0.936提升到0.964，而RMSE值则从1.338mg/L下降到0.926mg/L，表明该方法可将克里金空间插值法的RMSE值降低约30%，具有非常好的推广价值。采用该方法，可在不进行图像拼接的情况下准确地估测大型水体的水质参数，大幅度地降低了无人机遥感技术的探测难度，可成为当前水质调查技术的有力补充。在下一步的研究中，可以进行更多的案例以测试该方法的有效性。同时，也可尝试采用计算机视觉等技术对多光谱影像进行处理，以实现大型水体多光谱影像的有效拼接，从另一条途径解决无人机多光谱水质探测中的难题。