山东省弥河流域历史降雨统计规律分析

郭 成，刘 薇，王 沁，林 静

(1.山东省水利厅，山东 济南 250013；2.河海大学，江苏 南京 210098)

受气候变化和人类活动的影响，降雨量的时空分布规律发生了变化，导致一系列的水文响应。在此背景下，研究水文序列的统计规律，揭示其趋势性和跳跃性，具有重要的现实意义。

近年来，国内学者围绕水文序列的统计规律开展了大量研究。胡义明等以金沙江为例进行跳跃性分析，结果表明基于修正前后序列所进行的统计规律分析存在明显的差异性；郝婷婷等对淮河近50年的径流演变规律进行分析，得到了淮河流域四个区间的变化趋势、突变年份、变化周期；张少文等对黄河长期径流数据进行研究，验证了小波分析在水文水资源系统分析中的实用性；于文金等对淮河流域暴雨的时空分布及趋势规律进行研究，结果显示淮河暴雨序列有着一定的周期性；赵双庆等以董志塬的年降水量为研究对象，研究结果表明董志塬的年降水量呈显著增加趋势，同时得到董志塬年降水量的突变年份和变化周期；刘惠英等以香溪河流域近60年的降雨量为研究对象，对其年、季变化趋势及突变进行分析，结果表明夏季降雨突变发生时间与年突变发生时间一致，春、秋、冬三季则多变。

国内研究主要集中在年降雨量或年径流量的统计规律，对流域降雨极值要素统计规律研究相对较少。本文以山东省弥河流域为研究对象，对其降雨极值序列进行统计规律分析，揭示其趋势性、跳跃性、周期性特点。

1 方法描述

本文分别采用Mann-Kendall趋势检验法和Mann-Kendall突变检验法开展趋势性、跳跃性分析。

1.1 Mann-Kendall趋势检验法

对于序列Xt=(x1，x2，…，xn)，∀i，j≤n且i≠j，假设H0：序列中数据无显著趋势；H1：序列存在上升或下降趋势。定义统计量S：

(1)

(2)

时间序列长度n<10时，直接使用统计量S进行双边趋势检验。

n≥10时，统计量S近似服从标准正态分布，构造检验统计量Z：

(3)

1.2 Mann-Kendall突变检验法

给定序列(xn，xn-1，…，x1)，Sk表示第i个样本xi>xj(1≤j≤i≤n)的累计数，定义统计量：

(4)

Sk的均值和方差分别为：

E[Sk]=k(k-1)/4

(5)

(6)

将Sk标准化：

(7)

其中UF1=0。给定显著性水平α，若|UFk|>Uα，则序列存在明显突变趋势，UFk可组成一条曲线。将序列反向排列，得到UBk=-UFk，其中UB1=0。

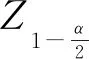
1.3 Morlet小波分析

本文选用复Morlet小波对弥河不同时段长面雨量进行连续小波变换。复Morlet小波的形式为：

(8)

式中，i—虚数；w0—常数，本文w0取6.2。

对于给定的小波函数ψ(t)，水文时间序列f(t)∈L2；(R)的连续小波变换为：

(9)

式中，a—尺度因子，反映小波的周期长度；b—时间因子，反映时间上的平移；Wf(a，b)称为小波变换系数。

将时间域上的关于a的所有小波变换系数的平方进行积分，即为小波方差：

(10)

小波方差随尺度a的变化过程称为小波方差图。它反映了波动的能量随尺度的分布。通过小波方差图，可以确定一个水文序列中存在的主要时间尺度，即主周期。

2 实例分析

2.1 流域概况

弥河流域位于潍坊市境内西部，流域面积3847.5km2，河长206km。弥河多年平均降水量为706mm，上游坡度较大，洪水暴涨暴落，中下游进入山前冲积平原，坡度变缓，易发生洪涝灾害，在寿光广陵乡南半截河村分为三股，主流至央子港口，最终流入渤海。

本文降水资料为山东省弥河流域内28个雨量站1951—2019年的降水量数据。

2.2 降雨量时间演变规律

2.2.1不同时段降雨量

按照研究流域的实际情况，将全年划分为汛前(1—5月)、汛期(6—9月)、汛后(10—12月)三个时间段，分别对面雨量的均值序列和总量序列进行趋势性、突变性的分析，结果见表1。

由表1可知，各时间段面雨量序列变化趋势均不显著，各个时间段的均值序列与总量序列对应突变年份基本对应。为了更清晰地展示各个时间段降雨量与年降雨量之间的关系，绘制多年各个时间段降雨量，如图1所示。

图1 全年及不同时段降雨量变化图

表1 全年不同时段面雨量均值和总量统计规律分析表

可以看出，汛期降雨量是全年降雨量的主要组成部分，且两者变化趋势相一致。由此可知弥河流域降雨量主要集中在6—9月，其余月份的降雨量相对较少，且大部分年份中，1—5月的降雨量多于10—12月的降雨量。从多年的数据来看，弥河流域没有明显的丰水年和枯水年，整体升趋势较为平稳。

2.2.2不同时段降雨极值

由图5可见，EM断路器内部触点导体与外壳金属部分的热点温度随负载电流的增大而增大，由于导体为热源，其热点温度均高于外壳。负荷电流小于10 A时，外壳与触头的温升变化不明显，随负荷电流增大，触头与外壳热点的温升逐渐增高，且增幅逐渐加大。在负荷电流为80 A时：FEM模型求得的导体热点温升是23.0 ℃，外壳温升是11.6 ℃，计算时间为20.5 s；所提热通道法求得的导体热点温升是25.0 ℃，外壳热点温升是12.3 ℃，计算时间为17.1 s，最大温升均满足技术规范要求[10]。所提方法与FEM法相比的误差较小，不超过8.6%，计算速度比FEM法稍快。

(1)趋势性分析

绘制弥河流域1951—2019年逐年面雨量过程线，并采用线性拟合法对其趋势性进行分析，以最大1日面雨量为例，线性拟合结果如图2所示。不同时段长降雨极值序列趋势性分析成果见表2。

图2 1951—2019年最大1日面雨量变化拟合曲线

表2 不同步长面雨量极值序列线性拟合趋势分析

可知，不同步长的面降雨量极值序列在年际上均呈增长趋势。

在逐年过程线的基础上，进行M-K趋势检验。取显著性水平α=0.05，不同步长面雨量年极值序列M-K趋势检验总结见表3。

表3 不同步长面雨量极值序列M-K检验趋势分析

可见年最大1、3、7、15日降雨量统计值U分别为0.29、0.13、0.15、0.24，均不超过1.96，因此未通过置信度95%的显著性趋势检验；不同步长的面降雨量年极值序列在年际上均呈增长趋势，但未表现出显著性特点。

结合线性拟合法和M-K趋势检验结果，可以得出：1951—2019年弥河流域年最大1日、3日、7日、15日降雨量呈增长趋势，但趋势不明显。

(2)突变性分析

对1951—2019年不同步长降雨量极值数据进行M-K突变检验，以年最大1日面雨量为例，M-K统计量曲线如图3所示。

图3 弥河流域年最大1日面雨量M-K统计量曲线(1951—2019)

表4 不同步长面雨量极值序列突变性分析

图4 弥河流域年最大1日面雨量累积距平曲线(1951—2019)

(3)周期性分析

小波方差代表不同尺度扰动的强弱，其中较强的扰动极大值可以作为水文要素的主周期。采用小波分析对不同步长面雨量年极值进行周期性分析，最大1日小波方差变化曲线如图5所示。

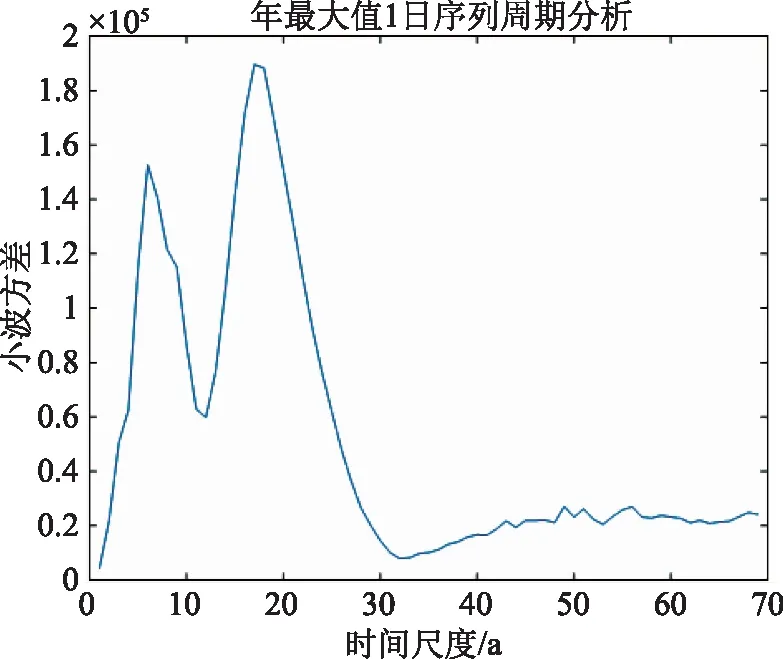
图5 最大1日降雨量小波方差变化曲线

由图5可知，年最大1日面雨量序列主周期有17a和6a。不同时间步长对应主周期见表5。

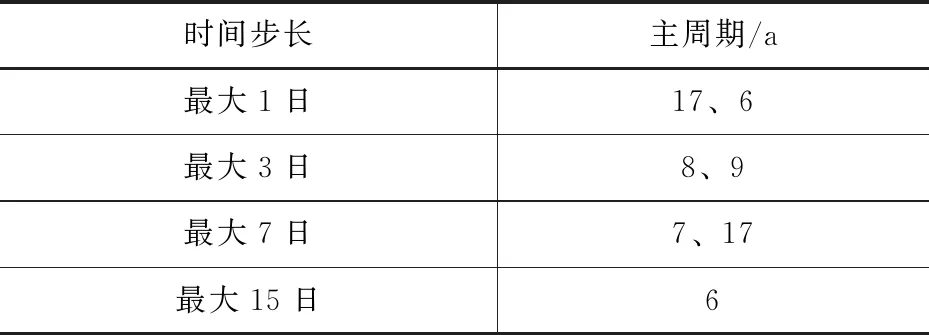
表5 不同步长面雨量极值序列突变性分析

由表5可知，年最大1日面雨量序列主周期有17a和6a，年最大3日面雨量序列主周期有9a和8a，年最大7日面雨量序列主周期有7a、17a，年最大15日面雨量序列主周期是6a。

3 结语

本文以弥河流域为研究对象，开展了不同时段长降雨极值序列的趋势性、跳跃性和周期性分析，主要结论如下：

(1)弥河流域的降水量主要集中在汛期(6—9月)，多年降雨量无明显变化趋势，弥河流域无明显的丰水年和枯水年之分。

(2)趋势性分析表明，弥河流域的年最大1d、3d、7d、15d降雨呈现上升趋势，但趋势性并不显著。

(3)弥河流域多年降水量存在跳跃性变化。年最大1d面雨量的突变年份为1962年、1973年；年最大3d面雨量的突变年份为1962年、1992年、2012年；年最大7d面雨量的突变年份为1962年、1993年；年最大15d面雨量的突变年份为1961年。不同步长面雨量年极值序列发生突变的时间多变、无明确规律性。

(4)弥河流域多年降雨量存在周期性。年最大1d面雨量的序列主周期为17a和6a；年最大3d面雨量的序列主周期为9a和8a；年最大7d面雨量的序列主周期为7a和17a；年最大15d面雨量的序列主周期为6a。结合不同步长面雨量年极值序列周期分析，弥河流域面雨量主要受7年和17年的周期影响。