基于小波变换方向性分量重构的复杂环境公路裂缝识别方法

王 兴

（山西省交通规划勘察设计院有限公司，山西 太原 030032）

0 引言

近年来随着我国交通基础设施的迅速发展，公路路面养护与管理工作也越来越复杂，尤其是对于公路裂缝的检测与修复，不仅检测的里程越来越多，裂缝检测的环境也日益复杂[1]。基于视觉采集的公路裂缝以图像形式呈现，因此裂缝检测最终归于图像处理问题。而在公路裂缝图像处理中，常有光照不均匀、交通基础设施阴影、水迹、污渍、车道线等影响，给裂缝检测带来很大的干扰[2]。裂缝具有较强的方向纹理特征，而小波变换在方向纹理性检测与分析方面具有较好的效果[3]，因此可以在公路裂缝检测过程中使用小波变换获取一部分特征信息。小波变换将原来图像分解成不同尺度的系数。小波是多分辨率理论的分析基础，其特点是能够在其他分辨率下发现某一分辨率下无法发现的特征。该文根据小波变换这一特征对公路裂缝图像进行小波分解，得到不同频率下的图像信息，根据方向性分析提取不同裂缝的特征信息，利用特征信息进行图像重构，从而滤除不相干的干扰，利用特征重构图像进行裂缝检测，能在很大程度上去除杂波与干扰，突显裂缝信息。

1 二维小波变换算法

1.1 二维小波变换

设φ（x1，x2）为二维小波基，φa；b1，b2（x1，x2）为φ（x1，x2）的尺度伸缩与二维位移[4]，则：

从上式可以看出，二维小波变换能伸缩、能旋转，并且还有“极化”的性能。因此小波变换在图像处理中能对图像分解、增强、去噪、压缩、融合等，从时频域获取图像更多的隐藏信息。

将图像进行二维小波变换的思路如图1所示：对图像每一行进行一维小波变换，能获得原图像O的水平方向参数，分别为低频分量L与高频分量H；再对变换后的图像O（L，H）每一列进行一维小波变换，能获得原图像的水平方向与垂直方向参数，即低频分量LL与高频分量HH；同时在交叉方向上能获得高频分量LH与低频分量HL。其中，HH代表水平和垂直方向的高频分量，表明了对角线方向的细节信息；LH代表水平的低频与垂直的高频参数，该参数表明了垂直方向的细节信息；HL代表水平的高频和垂直的低频参数，该参数表明了水平方向的细节信息[5]。

图1 二维图像小波变换分解示意图

在图1中，还能继续对低频分量做二维小波变换实现二级分解，此外根据需求还能对低频分量做更多级的分解。以上的分解实质上是对图像做多尺度分析，当尺度越来越小时，能获取越来越细微的细节信息。从图中还能看出，随着分解尺度越来越小，图像尺寸也越来越小。这是因为随着在第一层下采样到第二层，下采样过程中丢失了部分信息，这些丢失的信息实质上是高频信息，而这些高频信息在分解过程中能通过高频分量保存。

如图2所示，将一幅房屋图像进行二级小波变换，首先将图像进行行与列分解，得到了图像中隐藏的水平分量信息，从图中可以看出图像纹理信息偏于水平方向，尤其突显了图中屋顶瓦片的纹理信息，而第一层的垂直高频分量能明显看到房屋的垂直轮廓边界信息，但是屋顶瓦片纹理不明显，第一层的对角高频分量体现了图像中的对角方向纹理信息，同时也能看到图像中有大量噪点。结合第一层水平高频分量与第一层对角高频分量可知屋顶瓦片的纹理信息较明显，说明屋顶瓦片图像含有大量水平高频分量与对角高频分量，两者结合体现了瓦片的细节。再将第一层小波变换获得的低频分量进行二级分解，从图中能看出低频分量较完整地显示了图像大部分信息，而水平高频、垂直高频与对角高频分量信息进一步刻画了对应方向的细节。

图2 图像小波变换分解实例

1.2 小波变换重构算法

小波变换重构过程分别对小波变换获得的结果图像每一列与每一行先后进行小波逆变换，能够重构原来图像。其中二维小波逆变换公式为[4]：

事实上对图像进行二维小波变换，获得大量不同尺度不同方向不同频率的分量信息，其目的是对这些分量信息根据需求进行取舍，如对图像进行去噪，则能将提取出的高频噪声信息剔除，保留去噪后的分量信息，对这些信息进行重构，能获得去噪后的图像信息。

图3中对原始图像进行如图2所示的二级小波变换，仅利用第二层低频变换结果进行图像重构，比较重构图像与原始图像可以看出，重构的图像逼近于原始图像，但是重构图像中少了墙面的高频噪点信息。

图3 使用低频分量重构图像

2 不同方向分量公路裂缝识别方法

考虑到公路裂缝所处环境复杂，对公路裂缝图像进行处理，会存在大量的沥青噪点、车道线干扰等的影响，使得裂缝提取难度大。但是公路裂缝具有方向特征，能利用二维小波变换中的尺度旋转进行检测。

从图4可以看出，对图像进行不同方向不同尺度的分解后，可以结合公路裂缝的特征如方向性、频率选择性等进行特征信息提取。假设图像中裂缝为横向裂缝，可以从一级分解或二级分解中的水平方向高频分量获取裂缝特征，水平高频图像中将突显水平方向裂缝信息而抑制其他方向信息，实际上可将小波分解看作对图像做方向滤波，保留了水平方向的信息。因此根据公路裂缝图像分解出的水平高频信息重构图像，能减少裂缝检测的干扰。

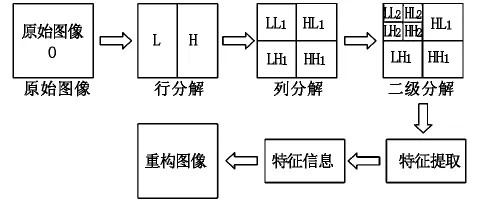
图4 多尺度重构图像流程图

对重构图像的裂缝检测可使用边缘提取方法，由于这时提取的裂缝边缘是二值图像赋值，裂缝在图像中以断续二值体现，因此还需要对检测到的裂缝特征进行拼接，同时根据拼接算法剔除边缘检测中的杂波。裂缝拼接主要是确定像素的连通域以及裂缝生长规律[6]。在二值图像中，可以将像素值1作为相邻连接，那么令S={1}。常用的相邻连接规则有：

a）4邻接 像素q∈N4(p)，那么像素p和q是4邻接的。

b）8邻接 q∈N8(p)，那么像素p和q是8邻接的。

c）m邻接 (i)q∈N4(p)，或者(ii)q∈ND(p)，集合N4(p)∩N4(q)没有S值的像素，那么像素p和q是m邻接的。

对于集合C，假设Y为包含在集合C中的连通分量，B为初始结构元素，那么通过迭代方法将能生成连通分量中的所有元素：

如果Xj=Xj-1，则收敛，这时Y=Xk，再根据上式继续迭代。

3 实验结果分析

分别以横向公路裂缝与纵向公路裂缝为例验证提出算法。横向公路裂缝方向偏于水平，图像中左侧有白色车道线，且图像中有明显的片状沥青噪点，对图像进行二层小波变换，从第一层小波变换水平高频分量与第二层小波变换水平高频分量可以看出，图像中仅有比较明显的横向裂缝。从第一层小波变换垂直高频分量与第二层小波变换垂直高频分量可以看出，图像中仅有比较明显的垂直车道线轮廓，而无横向裂缝，如图5所示。

图5 公路裂缝图像二级小波变换各分量图

使用水平高频分量作为横向裂缝的特征信息重构图像，如图6所示，重构的图像中因为没有垂直分量而只含横向裂缝信息，以此重构图像作为裂缝检测图像，其结果如图7所示，可以看出检测到的裂缝纹理均为水平方向，但是除了裂缝纹理还存在横向纹理杂波。采用连通域裂缝生长算法能根据连通阈值滤除杂波，并按照横向裂缝纹理拼接裂缝。

图6 使用水平分量重构图像

图7 横向裂缝检测拼接

针对纵向裂缝与有纵向车道线的公路裂缝图像，原始图如图8所示，用本文提出方法能使用垂直分量重构图像，包含了车道线轮廓纹理与裂缝纹理信息。此时根据垂直分量重构图像检测出的裂缝还包括了垂直分量杂波与车道线信息。在裂缝拼接过程中设置两条疑似裂缝之间的角度阈值不为0，则可除去车道线轮廓纹理，这是因为车道线轮廓为笔直竖线，与裂缝的小幅度弯曲不同。拼接后的裂缝图像如图9所示，有较好的检测效果。

图8 使用垂直分量重构图像

图9 纵向裂缝检测拼接

4 结论

针对有车道线干扰的公路横向裂缝与纵向裂缝图像，使用小波变换获取了二级小波分解特征，并根据横向裂缝与纵向裂缝的方向性选择了水平高频分量与垂直高频分量对图像进行重构，重构图像中抑制了其他干扰信号，仅保留了与裂缝方向性一致的高频分量信息，再对重构图像进行裂缝检测与拼接。当裂缝方向性与车道线方向性相似时，采用设置裂缝拼接角度阈值的方法去除直线型车道线轮廓。