高分子纺织材料热湿传递性能数学建模预测及研究

何 潇

（陕西财经职业技术学院，陕西咸阳712000）

目前，计算机建模技术得到软硬件技术有效推动，其应用领域也在逐步扩大。模拟仿真技术根据几何、环境以及性能相似原理，通过数学模型或物理模型展开相关实验。数值模拟试验能够掌握全方位复杂数据，并对数据进行评估与研究。因此，针对高分子纺织材料的设计与研究可以通过建立数学模型来实现。由于高分子纺织材料主要应用于高温、高湿、高辐射环境下，且此类环境会对人体生理产生不定量的负面影响，需要对所用防护织物进行优化设计。利用数学模型，模拟人体表面在工作环境下的温度变化，并将改进后的高分子纺织材料进行同步测试，为热防护服的设计与开发提供模型支持。

1 高分子纺织材料优化数学建模必要性

1.1 纺织材料设计

高分子纺织材料的设计是从科学角度分析织物的热性能，然后根据设计目标确定物理参数，例如织物的厚度、孔隙率以及材料。目前，人们对纺织材料的要求有所提高，纺织材料不仅需要满足人体屏蔽和保暖的要求，而且还更加注重衣物的舒适性，例如热湿舒适性、压力舒适性等。以关注度最高的温湿度为例，在低温或室温环境下，人体舒适度可通过人体皮肤与织物之间的微小气间隙来衡量人体的热舒适性指数，包括温度、相对湿度、风速等。但是对于某些功能性纺织材料，这些舒适性考虑因素并不一定适用。对于热防护服，其工作环境通常具有高热量和高湿度的特征，不宜考虑人体的热湿舒适度，因为大量出汗并不能提供给人体常规热湿舒适度。实际上，与火灾现场温度强度相比，由出汗等原因引起的不适感并不属于必要性的考量因素。关注点更偏重于消防员的人身安全，即高分子纺织材料的设计原则应以减轻人员灼伤度或避免人员灼伤为目标[1]。

1.2 热防护服

热防护服的正确使用可以减轻热源对人体的损害，消防员、军事领域以及赛车行业使用热防护服的频率较高，以保护消防员和其他应急人员免受其工作危险的伤害。当皮肤温度达到44℃时，人们会感受到烧灼感。因此，有必要对热防护服内部热湿传递规律进行充分了解，以便为高分子纺织材料设计成热防护服提供理论参考[2]。

在环境温度处于常规温度区间时，宜使用经典热湿传递定律来描述织物中的热湿传递。但是，在高温高湿的环境中，热湿传递速率明显高于常温环境。防热服通常由外层、隔热层以及内层组织构成。在此基础上，通常还会额外添加防水层，形成四层织物组织结构。另外，特殊织物有一定概率存在分形结构，这使高分子热防护织物在加热过程变得更加复杂。因此，应基于现有的数学模型，对高分子织物数学建模进行物理定律研究。

2 高分子纺织材料数学模型建立基本类 型与要素

2.1 数学建模方法类型概述

数学模型的建立是展开织物热传性能数值模拟的基础，建模方法主要包括几何方法、物理方法以及混合方法。早期主要基于织物的几何特性进行模型建立，该方法具有仿真速度快的优点，但是它没有充分结合织物的物理特性进行计算。

数学模型是根据高分子纺织材料热传性能的数学模拟建立的。近年来，基于物理特性的建模方法是织物建模发展的重点。尽管计算复杂，但是它具有3D配置和动态仿真的优势操作，效果更贴近实际情况。混合建模方法是建立在几何方法与物理方法共同结合的基础上，主要应用于纺织领域研究的初级阶段。将几何方法与物理方法相结合就构成混合建模法，但这一方法主要应用于初期阶段的高分子纺织材料研究中[3]。

2.2 热传递基本要素与理论

2.2.1 热传导

热传导现象的产生是建立在单一物体或相邻两个物体之间在温度梯度下出现的内容交换，傅立叶定律计算公式是热传导的计算依据，公式如下所示[4]。

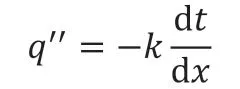
公式中，q''代表热量流动密度；k代表导热系数；负值代表热量转移方向为向低温方向。

2.2.2 热对流

热对流是物体表面与其周围环境之间存在的温度差而产生的热量交换。热流量类型有两种，分别是自然对流与强制对流[4]。热对流公式如下所示：

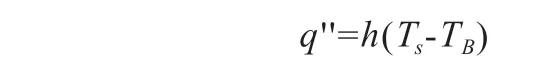
公式中，h代表对流热量传递系数；Ts代表物体表面温度；TB代表物体周围环境温度。

2.2.3 热辐射

热辐射是指通过电磁能的发射，使另外物质吸收电磁能，并将电磁能转换成热量的现象。在热辐射中，需要重点研究两个或两个以上对象之间产生的辐射，且任一对象均会在发射电磁能的同时吸收相应热量[5]。热传递计算方程式如下所示：

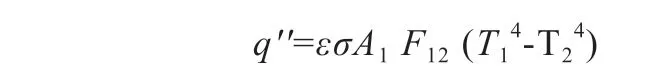
公式中，q代表热流率；ε代表辐射率；σ代表公式中的常数；A1代表辐射面1的面积；F12代表辐射面1-辐射面2的形状系数；T1与T2分别代表辐射面1与辐射面2的绝对温度。

3 高分子纺织材料热湿传递数学建模分析

3.1 数学模型建立

完善优化高分子纺织材料热传效能的数学模型能够向同类型热防护产品的制备与评估提供先进、便捷的改革基础。目前，国内外大量研究团队已经通过数值方法对高分子纺织材料材料的隔热性能测试展开试验。

在创建数学模型时，引入有限体积法，需要将纺织材料视作初阶三角形模型，并在此基础上进行稳态热分析，但是，该方法的缺点是不能简洁明了展现出纺织材料实际具备的热传效果。因此，为改进数学模型的建立效果，对热传模型进行简化构建，规划出简化版一维热传导模型。在简化版模型中，将纺织材料视作平面四边形，通过ANSYS软件分析纺织材料的瞬态热传性能，分析判断高分子纺织材料在不同温度环境下所产生的隔热成效[6]。通过对流量流动密度展开仿真模拟，可以得出仿真模拟结果与测试结果之间的误差小于5%。高分子纺织材料热湿传递模型如图1所示。

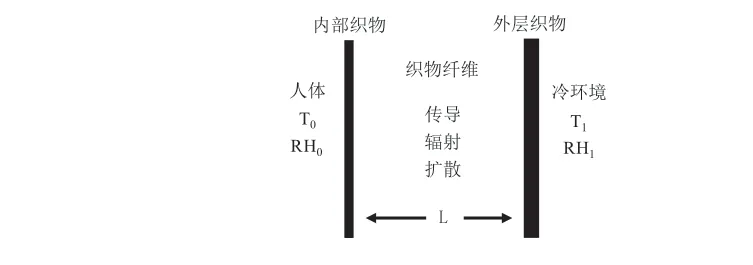
图1 热湿传递模型Fig.1 Heat and humidity transfer model

可以将高分子纺织材料视为匀质平板，此模型结合了水分与温度对纺织材料热传性能的影响因素。模型中的能量传递方式有两种，分别是热传导与热辐射。在热湿传递数值模拟的基础上，经研究发现，影响热流量的主要因素是初始含水量、纤维层厚度以及环境温度。在三维数学模型的基础上，预先判断超湿纺织材料在逐渐干燥过程中产生的温度与水分分布，并将高分子纺织材料热湿传递模型与CFD进行结合[7]。数值仿真模拟结果为：该模型对于不同环境下纺织材料的温度与水分分布变化进行准确预判。

通过有限差分法和有限元法模拟高分子纺织材料的热传模型，建立火灾情况下的一维径向热传圆筒形模型，如图2所示。

图2 一维径向热传圆筒形模型Fig.2 One-dimensional radial heat transfer cylindrical model

假设人体为圆柱体，则根据实际情况在纺织材料与皮肤之间设置一小层空气层，形成“织物-空气层-皮肤”的物理结构模型。用有限差分法对模型展开数值模拟。织物表面温度的模拟结果与实验结果一致。此模型在保护设备防热设计中提供架构参考，但没有将水分含量对热传性能的影响进行充分考虑。通过建立稳态热湿传递数学模型，利用有限元算法构造了非线性常微分方程和一维最小化问题直接搜索方法，并将两种方法耦合，得出正则迭代算法。对差异化实验条件下数学模型进行模拟测算，获得了Hooke-Jevees直接搜索方法。此方法可以实现双层高分子纺织材料形式设计反演问题的准确处理。同时，数学仿真模拟实验进一步明确算法对反演问题合理表述的正确性与有效性。

3.2 皮肤热传模型

热防护织物主要用于降低织物上的热传递率，在评估热防护织物或热防护服的防护性能时，应考虑热量在人体皮肤上的积累和传递效果。皮肤热传模型的建立可以模拟人体皮肤的热传效果，通常情况下，人体皮肤的热传由Pennes’模型进行模拟[8]，热方程如下：

公式中，ρs代表皮肤密度；cps代表皮肤比热容；ks代表表皮导热系数；ρb代表血液密度；cpb代表血液比热容；ωb代表血灌注率。

分析皮肤模型数值变化对热防护产品应用性能的影响变化效果可知：当皮肤模型与初始化表层温度出现差距时，高分子纺织材料的热防护性也会呈现出较大变化。因此，选择针对性明确的皮肤模型，并将模型进行标准化处理能够为热防护检验效果起到积极作用。

3.3 数值仿真模拟计算

针对热传性能研究领域中导热问题的解决办法包括数值解法、分析解法以及近似分析解法。数值解法主要应用于几何形状纺织材料的导热计算中。一般情况下，数值解法将用于极端纺织材料的湿热微分方程中。结合热湿传递耦合数学模型探究出能够应用于实践操作的数值求解方案。研究人员针对织物数值模拟求解提出了热湿耦合强非线性方程组。首先将方程组解耦，然后将原始方程拆分为多元非线性方程组，根据牛顿迭代法计算出高分子纺织材料内部温度分布、水蒸气通量分布以及水蒸气压力，计算结果表明数值结果与实验数据一致，表明此法具备可行性与应用型。为了测算出差异化环境下不同纺织材料的温度、水蒸气浓度以及水分含量，提出了一种隐式迭代算法，以此来求非线性偏微分方程的解[9]。

3.4 热湿传递性能测试方法

数值模拟方法为解决热传和水分传递的复杂分析和计算提供了一种有效的方法，数值模拟的有效性已通过常规实验方法得到验证。目前，织物热传和热传性能的主要测试方法包括：织物微气候测试仪、热防护性能测试仪（TPP）、燃烧假人、微型CT扫描仪等。织物微气候仪可以快速测量织物、皮肤、空气层与外部环境温、湿度的动态变化；热防护性能仪需要将织物样品置于具有可控热流的模拟火场中，通过织物后方的热流传感器，记录假体皮肤达到二度灼伤所需的市场，以此作为评估织物热防护性能的主要依据；在燃烧假人实验中，通过假人表面的热流传感器来收集实验相关数据，以便分析评估高分子纺织材料的综合热防护成效。微型CT是通过X射线断层扫描来分析材料内部结构与材料组成。如利用CT扫描仪观察潮湿木材的动态干燥过程，从而得到内部水分含量分布成像[10]。

4 结语

从国内外高分子纺织材料热传数值模拟研究现状可看出，织物热传模型在二维坐标系下进行建立，并不能全面反映织物几何结构，仿真结果与实际热传过程存在一定偏差。基于此，高分子纺织材料热湿传递数学模型仿真模拟优化方向应转移至三维结构模型的研究中，结合多类纺织材料的本质特征建立相适应的数学模型，并通过合理数值计算对比试验结论与模拟结果，实现高分子纺织材料热湿传递三维数学模型的建立。