一种表面效应和非局部效应耦合的静电纺丝纤维拉伸力学模型*

原 波, 何显运,张 涛

(1 广东工贸职业技术学院 机电工程学院， 广东广州510510; 2 河北机电职业技术学院 机械工程系, 河北邢台 054000)

静电纺丝是制备生物医用薄膜材料的一种重要方法，静电纺丝工艺获得的纤维薄膜具有非常高的比表面积和极高的孔隙率，可以作为细胞生长载体,利用静电纺丝方法能够连续制备纳米级或亚微米级高分子纤维薄膜，对于生物医学组织工程支架设计具有重要应用价值[1]。

静电纺丝纤维薄膜力学强度必须满足其作为药物载体的要求，在使用过程中需要承受细胞移动造成的载荷，强度不足成为静电纺丝纤维薄膜在应用中的最大瓶颈之一，并且针对纳米尺度静电纺丝高分子纤维的实验过程中发现其力学性能具有尺度效应[2]。对于静电纺丝纤维力学性能所表现出的尺度效应，研究人员分别从不同影响因素进行了分析。一部分研究人员认为纤维材料内部结构的不均匀性产生了非局部效应，导致高分子纳米纤维力学性能表现出一定的尺度效应。非局部效应的产生最早由 Eringen和 Edelen提出，孙亮和原波等研究人员分别利用经典应变梯度模型和高阶应变梯度模型建立了高分子纤维在不同受力条件下的力学响应模型，并给出了纤维在弯曲变形中的尺度效应模型[3-4]。还有一部分研究人员认为，随着高分子纤维直径的减小，其比表面积会显著增大，因此材料的表面效应对于静电纺丝纤维力学性能的影响相比于宏观材料更加明显，研究人员根据表面效应理论模型构建了纤维的力学性能与其特征尺寸之间的关系，并解释了高分子纳米纤维在外界载荷作用下所表现出的力学尺度效应[5-6]。

静电纺丝纤维在实际的力学环境中，其力学特征量不仅会受到纤维内部结构不均匀的影响，而且同时也会受到表面效应的影响，现有的理论模型缺乏对以上两种因素的综合考量。针对高分子纳米纤维的力学性能研究迫切需要建立一种能够同时考虑两种效应影响的力学模型，即表面效应和非局部效应耦合模型，才能更加准确地计算分析纳米纤维的微观力学性能[7-8]。本文在前期的研究工作基础之上，在静电纺丝纤维拉伸变形应变能中计入表面效应和非局部效应的影响，研究两种效应耦合情况下静电纺丝纤维的尺度效应模型。研究结果有望对静电纺丝纤维材料弹性模量尺度效应的产生原因进行分析，为研究高分子纳米纤维材料的力学特征提供理论分析工具，并建立一个用于分析静电纺丝纤维材料变形过程中的力学模型。

1 应变梯度和表面效应耦合的纤维拉伸 力学模型

如图1所示，长度为L直径为D的静电纺丝纤维受到轴向载荷F 作用，其在x方向的位移用u表示，应变用u'表示，应变的梯度用u"表示。

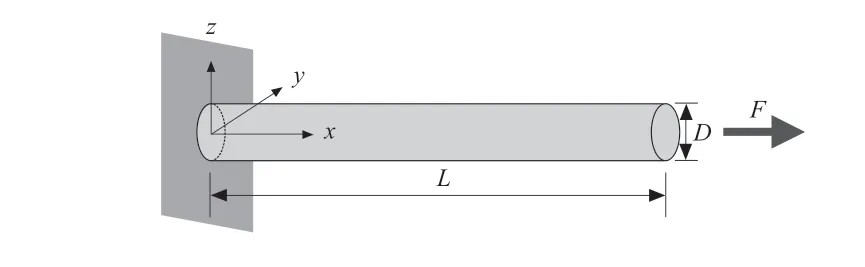
图1 高分子纳米纤维拉伸变形示意图Fig. 1 Tensile Deformation of polymer nanofibers

根据表面效应理论及非局部效应理论模型，分别计算两种效应在纤维拉伸变形过程中所产生的应变能并进行耦合，静电纺丝纤维在轴向载荷作用下的总应变能U可以表示为：

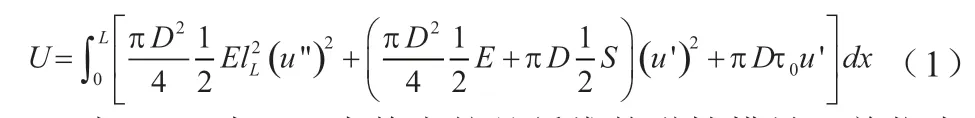
式（1）中：E为静电纺丝纤维的弹性模量，单位为 Pa；lL表述纺丝纤维的特征参数，单位为 m；S为纤维材料的表面弹性系数， N/m；τ0为纤维材料的初始应力，N/m。

式（1）经变分后可以得到：

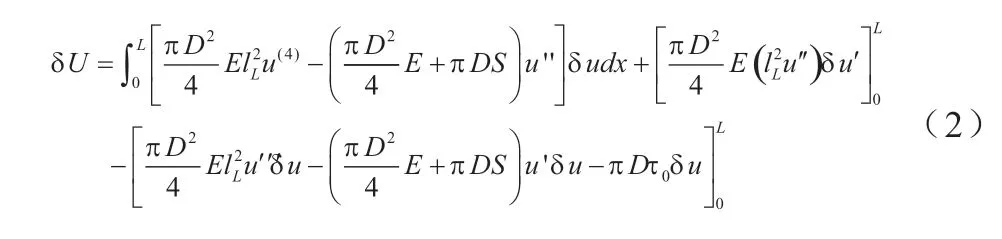
轴向载荷F对纤维做功W的变分形式可以表示为：

利用变分原理δ(U-W)=0，可以得到如下表达式：

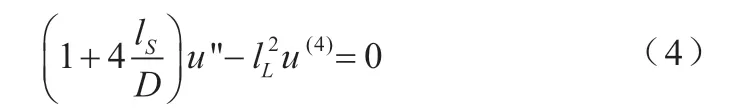
其中ls表示纺丝纤维的表面模量与弹性模量的比值，单位为m；在轴向载荷F作用下静电纺丝纤维的边界条件可以表示为：

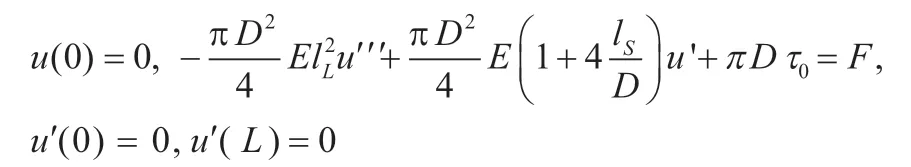
根据边界条件求出方程（4）的解为：

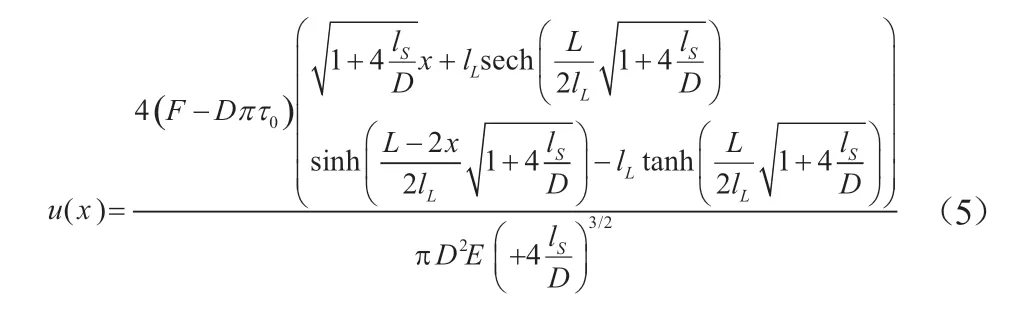
即为表面效应和非局部效应耦合情况下静电纺丝纤维在拉伸变形中的位移表达式。

根据式（5），静电纺丝纤维的总伸长量ΔL可以表示为：

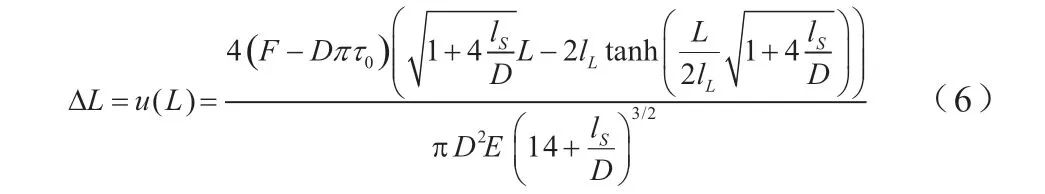
轴向载荷F与静电纺丝纤维总伸长量ΔL之间的关系式如式（7）所示：

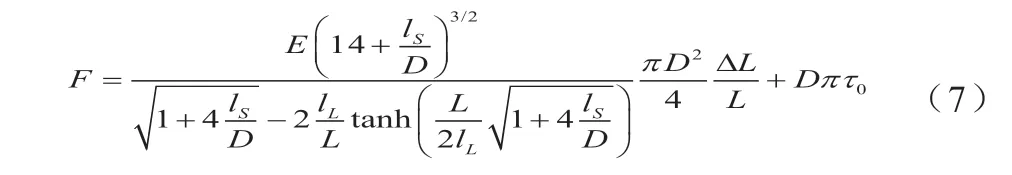
进一步可以计算出表面效应和非局部效应耦合情况下静电纺丝纤维的等效弹性模量Eeff，如式（8）所示：

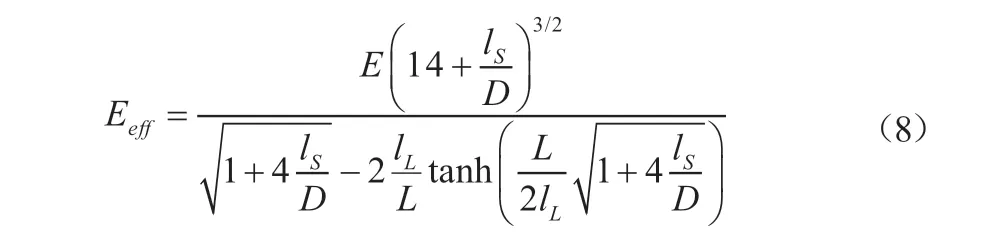
2 模型分析

根据式（8），在表面效应和非局部效应耦合情况下，高分子纳米纤维的等效弹性模量与纤维的长度和直径变化趋势具有一定的关系，如图2所示。从图2中可以看出，随着静电纺丝纤维的直径D和长度L的减小，纺丝纤维的等效弹性模量呈现不断增长趋势。

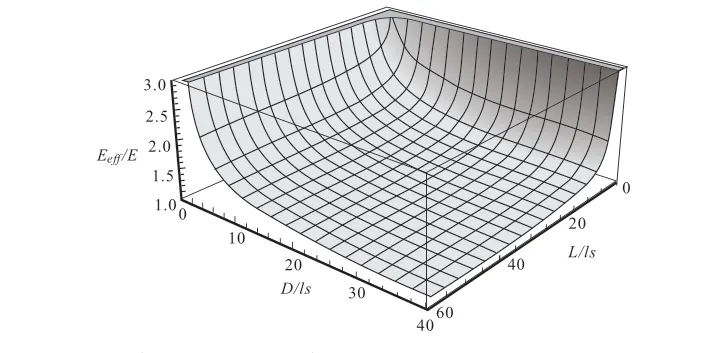
图2 表面效应和非局部效应耦合情况下纤维等效弹性模量的变化规律Fig. 2 Variation of fiber equivalent elastic modulus under coupling of surface effect and nonlocal effect

在图2中，高分子纳米纤维的直径和长度是两个独立的量，但是实际情况下，为了方面高分子纤维的拉伸实验操作，所选取纺丝纤维的长径比不能低于临界值，在模型分析过程中，选取长径比L/D≥10的纤维作为分析对象，图3 给出了三种不同长径比条件下的纺丝纤维弹性模量的计算结果，纤维的等效弹性模量与长度L和直径D之间的关系 (假设ls=lL)。

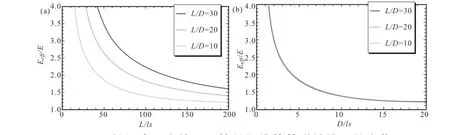
图3 长径比固定情况下纺丝纤维等效弹性模量的变化Fig. 3 Variation Trend of equivalent elastic modulus of spinning fiber with fixed aspect ratio

从图3 (a) 中可以看出，纺丝纤维的等效弹性模量均会随着纤维特征长度的减小而增大，在三种不同长径比的情况下，等效弹性模量的增长趋势不同。从图3(b) 中可以看出，纺丝纤维的等效弹性模量均会随着纤维特征直径的减小而增大，并且等效弹性模量的增长趋势与纤维的长径比无关。

3 结论

（1）根据表面效应理论和非局部效应理论，通过在应变能中计入两种因素的影响，建立了表面效应和非局部效应耦合情况下纤维拉伸变形的力学模型。

（2）模型计算结果显示，在长径比确定条件下，纺丝纤维的等效弹性模量会随着纤维特征长度的减小而增大，并且等效弹性模量的增值趋势与长径比大小有关；纺丝纤维的等效弹性模量也会随着纤维特征直径的减小而增大，并且等效弹性模量的增长趋势与纤维的长径比大小无关。

（3）该模型为高分子纳米纤维材料的力学特征研究提供理论分析工具，有望用于静电纺丝纤维材料在实际使用过程中的力学结构设计参考。