“鹅颈”式有限转角导电滑环疲劳特性研究

刘明 ，孟立新 ，张立中 ，陈力兵 ，张兆元

（1.长春理工大学 机电工程学院，长春 130022；2.长春理工大学 空地激光通信技术国防重点学科实验室，长春 130022）

在反射镜二维伺服转台的研制过程中，为减少线绕力矩的影响，通常采用导电滑环，它是实现两个相对转动机构的图像、数据信号及动力传递的精密输电装置［1］。目前常用的铜环-电刷式导电滑环的摩擦力矩在牛米量级，其体积大、重量重，干扰力矩大，不能满足回转结构轻小型化和长使用寿命的要求。“鹅颈”式有限转角导电滑主要由滑环内环、滑环外环、柔性印刷电路板（FPC）组成，利用呈回转式排布于滑环内外环间的FPC来进行信号传输和电力传递，在内外环间设置挡环，起到对FPC导向作用［2］，结构简单，干扰力矩在毫牛米量级，具有使用寿命长、安装精度要求低等特点，可以弥补铜环-电刷式导电滑环的不足。

目前对于“鹅颈”式有限转角导电滑环的研究，P.-A.Mäusli等人［3］提出了一种导电滑环设计方案，设计内径为191 mm，外径为310 mm，扭矩15 N·m，但这种设计无法解决由电缆接头引起的滞后现象，存在正反转扭矩不一致的关键问题；Eric D.Miller等人［4］设计了一个激光通信用粗指向机构的“鹅颈”式导电滑环，经过试验测得其寿命优于3.30E+05 cycles（cycles物理意义为滑环回转次数）。张轶群等人［5-6］在某空间二维跟瞄系统的精密导电滑环研制过程中，设计了一种“鹅颈”式有限转角导电滑环，设计内径为80 mm，外径为100 mm，开展了导电滑环的疲劳寿命试验，试验行程为±7.5°，试验结果表明在进5.86E+06 cycles的疲劳试验后，导电滑环电阻值仍能满足指标，但是其并未对滑环的失效机理进行研究，没有对影响滑环使用寿命的因素进行分析，只是从试验角度对滑环的疲劳使用寿命进行测量。机械构件在工程应用中多在循环载荷下服役，疲劳寿命预测是结构设计中不可缺少的内容［7］，在常见的机械结构疲劳断裂事故中，交变载荷所造成的故障数占总数的80%以上［8］，贴附在内环上的FPC（FPC（内环））和贴附在“鹅颈”处的FPC（FPC（鹅颈））的交界处在滑环往复回转过程中承受高周交变应力，即使在保证静力结构安全的情况下，经历较长时间工作后，上述交界处也会发生疲劳失效破坏，从而影响滑环使用寿命。目前相关研究工作只是从试验角度对“鹅颈”式滑环的疲劳使用寿命进行测试，并未对滑环的失效机理和寿命模型进行深入研究。

本文针对“鹅颈”式有限转角导电滑环疲劳寿命预估难的问题，从滑环的疲劳失效机理分析出发，建立滑环的疲劳寿命预估模型，开展相关试验，为“鹅颈”式滑环疲劳使用寿命评估提供参考。

1“鹅颈”式滑环工作原理

“鹅颈”式有限转角导电滑环由内环、外环和FPC组成，FPC两端分别固定在内外环上，从而在内外环之间形成“鹅颈”，滑环结构示意图如图1所示。FPC由基材、导体层和粘结层组成，其中基材采用聚酰亚胺，导体层采用压延铜，传输信号和电力，粘结层采用环氧胶，根据传输信号路数和功率大小，分为单层FPC和多层FPC。FPC受导体层和基材层的张力，除“鹅颈”位置外，其余部分贴附在滑环的内外环侧壁上。为避免回转过程中张力不足引起FPC捻转，在内外环间设计有挡环，用于FPC形状保持。

图1 “鹅颈”式滑环结构示意图

“鹅颈”式滑环的安装方式和传统导电滑环一样，与反射镜二维伺服转台轴系直接连接，内环安装在轴上，外环安装在轴座上，或者，外环安装在轴上，内环安装在轴座上。图2为转台剖面图，图3为转台轴测图，为了压缩方位轴，安装方式选择前一种方式，将滑环外环与轴座作为一体，内环随轴旋转，轴带动俯仰轴系旋转。内外环之间除FPC连接外，其余部件不接触，利用转台轴系实现定位，不需要增加额外的轴承，装配精度要求低。FPC基材与滑环内外环材料之间的摩擦系数小，且为线接触，摩擦力矩小。FPC具有优良的动态弯曲性能，可以应用在需要长时间往复工作的工况下。

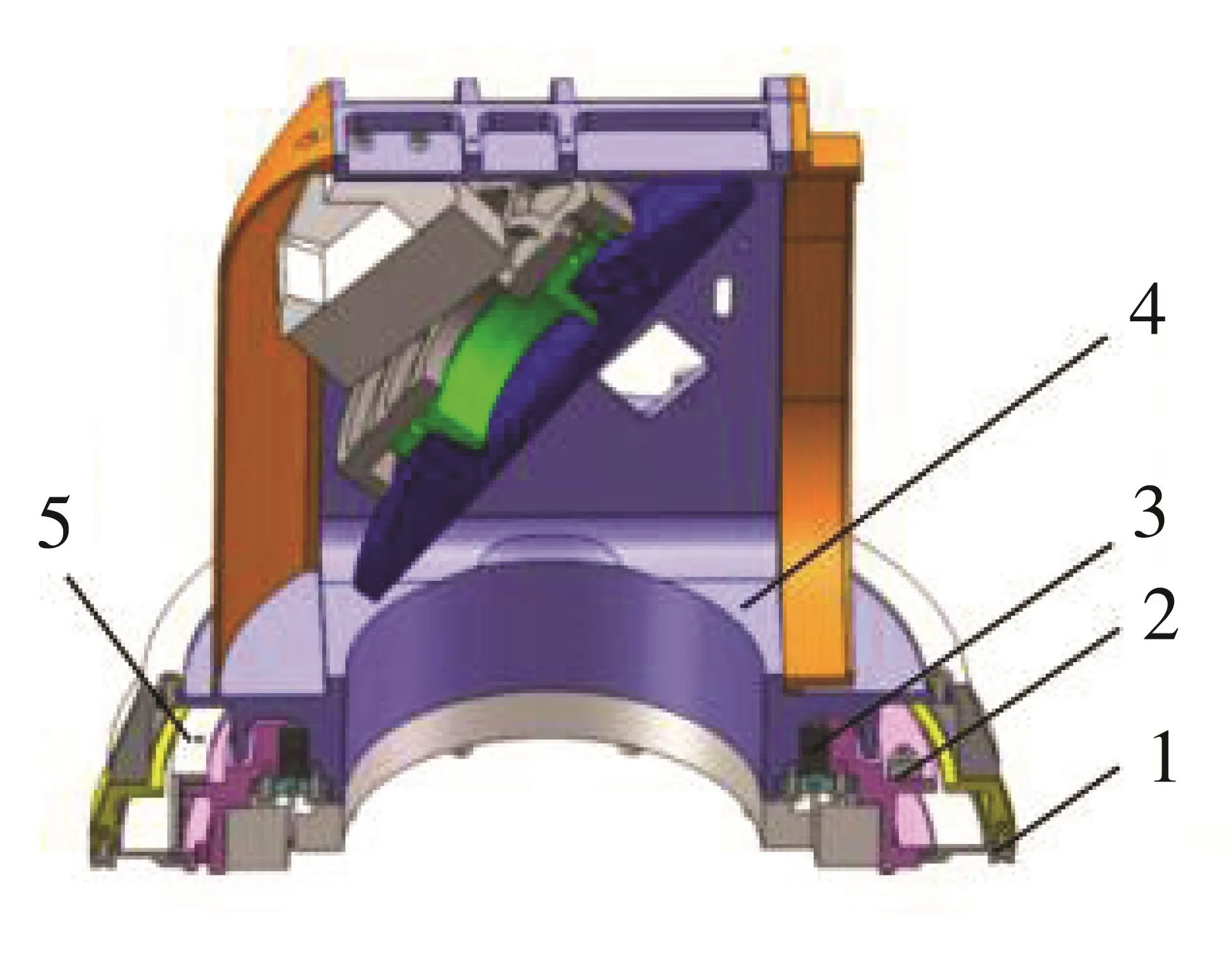
图2 转台剖面图

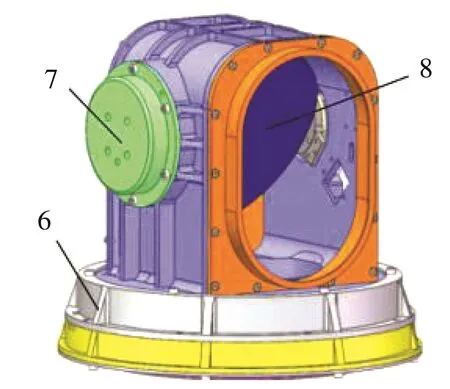
图3 转台轴测图

2 “鹅颈”式滑环疲劳寿命预估模型

2.1 运动受力分析

“鹅颈”式滑环在往复转动时，位于内外环间的FPC发生弯曲，FPC（内环）和FPC（鹅颈）交界处弯曲半径小，FPC导体层以中性面为界，向外的部分受张力，越往外张力越大，向内的部分受压力，越往内受到的挤压越严重，FPC分层示意图如图4所示。在高周交变载荷作用较长时间后，FPC在内外表面应力集中部位容易产生微小的裂纹，随着载荷作用时间的增加，裂纹开始扩展直至断裂失效，导致FPC传输信号失真甚至无法传输信号，最终影响滑环疲劳使用寿命。

图4 FPC分层示意图

式中，n为导体层层数；d为层间介质厚度；h为导体层厚度；Eb为导体层变形量；c为覆盖膜厚度；如图4所示。

在滑环设计过程中FPC（内环）和FPC（鹅颈）处要满足FPC最小弯曲半径要求：

图5 滑环运动受力示意图

2.2 寿命预估模型

目前用于分析疲劳损伤的理论方法主要有名义应力法、累积损伤理论和能量分析法等。名义应力法没有考虑缺口根部的局部塑形，且标准试件和结构试件之间的等效关系的确定比较困难，所以预测寿命和实际寿命有较大的出入［9］。累积损伤理论认为当应力低于疲劳应力的时候不会发生疲劳损伤［9］，这与实际是有出入的。能量分析法最初应用在混凝土的断裂耦合研究过程中，可以从能量平衡的角度，判定混凝土中裂缝是否扩展，通过分析裂缝扩展过程中能量的变化，判断裂缝的稳定性［10］，基于能量损耗定义损伤演化规则，可有效描述混凝土刚度退化规律［11］，相比于上述两种疲劳分析方法，能量分析法预测精度更高，计算简单，本文选用能量法来对滑环疲劳寿命进行分析。

定义FPC导体层能量释放率G为导体层裂缝扩展过程中增加单位裂缝长度和单位厚度所吸收的能量，在稳定状态下与物体弯曲半径直接相关。定义Γcriyical为FPC导体层临界断裂能，其物理意义是能使物体断裂的最小能量，可通过实验测定。当G>Γcritical时，即认为FPC导体层发生断裂破坏。FPC导体层能量释放率G主要来自滑环在回转过程中FPC的弯曲半径变化所对应的弹性势能GP的变化，可认为G=GP。弹性势能的大小与物体材料和弹性形变的程度有关，对应滑环的工作形式，在滑环外环半径R固定的情况下，即与导体层抗弯刚度D、滑环内环转动角度α和滑环内外环半径比ε有关。

当滑环内环转动α（0≤α≤ϕ）时，FPC（内环）线长的变化量为βr，FPC导体层弯曲弹性势能变化量GP为：

式中，κ为单元曲率；θ为滑环回转过程中任一位置FPC（鹅颈）处χ和χ'两点与滑环中心所连直线的夹角；λ为χ'点处的曲率半径。

结合GP与φ的关系，对式（3）进行求解：

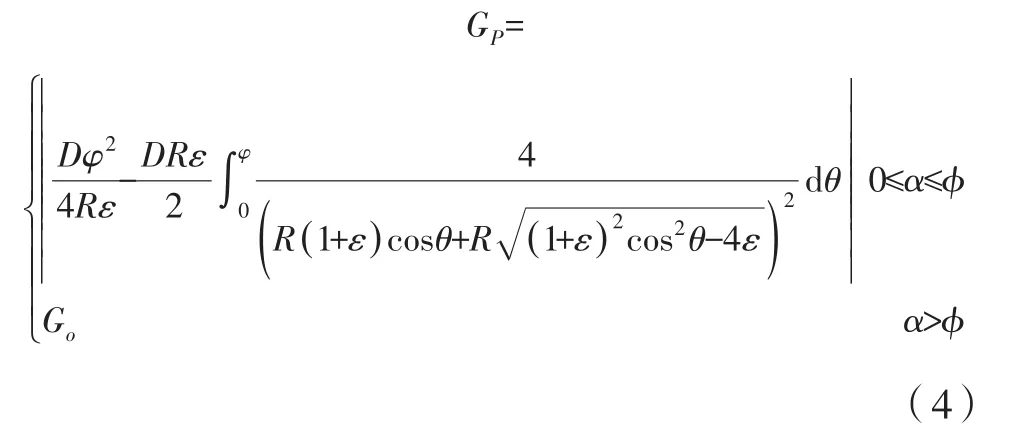
设滑环的疲劳断裂寿命为N，则当滑环转动N后，总的弹性势能变化量为NGP，故根据临界断裂条件有：

将式（4）代入式（5）即可得到滑环的疲劳使用寿命N。

3 疲劳寿命仿真

根据上文建立的预估模型，在滑环外环半径R一定的情况下，可以看出滑环疲劳寿命N与滑环内环转动角度α、内外环半径比ε和导体层抗弯刚度D有关，接下来分析上述各个因素分别对滑环疲劳寿命的影响。根据某二维反射镜精密伺服转台的实际设计要求，“鹅颈”式有限转角导电滑环部分设计仿真参数如表1所示。

表1 滑环设计仿真参数表

3.1 滑环内环转动角度α对滑环疲劳寿命N影响分析

从图6可以看出随着内环转动角度的增加，滑环疲劳寿命将大幅度减小，当增大到一定角度φ后，寿命N将趋于一个平稳值Nφ（Nφ并不是0，由于纵坐标量级是1010，较大，所以在图6中显示Nφ趋近于0）；通常情况下滑环临界回转角度φ值较小，工作范围会大于φ值，所以当滑环设计完成后，其疲劳使用寿命N一般情况下为一定值Nφ。

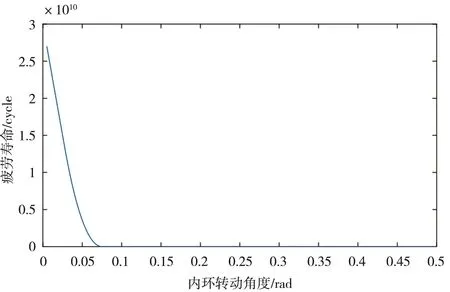
图6 疲劳寿命随内环转动角度变化图

3.2 滑环内外环半径比ε对滑环疲劳寿命N影响分析

在研究滑环疲劳寿命与内外环半径比的关系时，首先要保证FPC满足最小弯曲半径的要求。FPC依据导体层数量划分主要可以分为单面FPC和和双面FPC，层数过多会使FPC硬度变大，影响柔性。将表1中数据代入式（1）-式（2），分别令n=1和 2，r的取值范围分别为［5.9，88.2］和［28.5，43.0］，ε的 取 值 范 围 分 别 为［0.059，0.882］和［0.285，0.430］。为了使滑环具有较多通电路数，本文选用双面FPC进行仿真，得到滑环疲劳寿命随内外环半径比变化图，如图7所示。

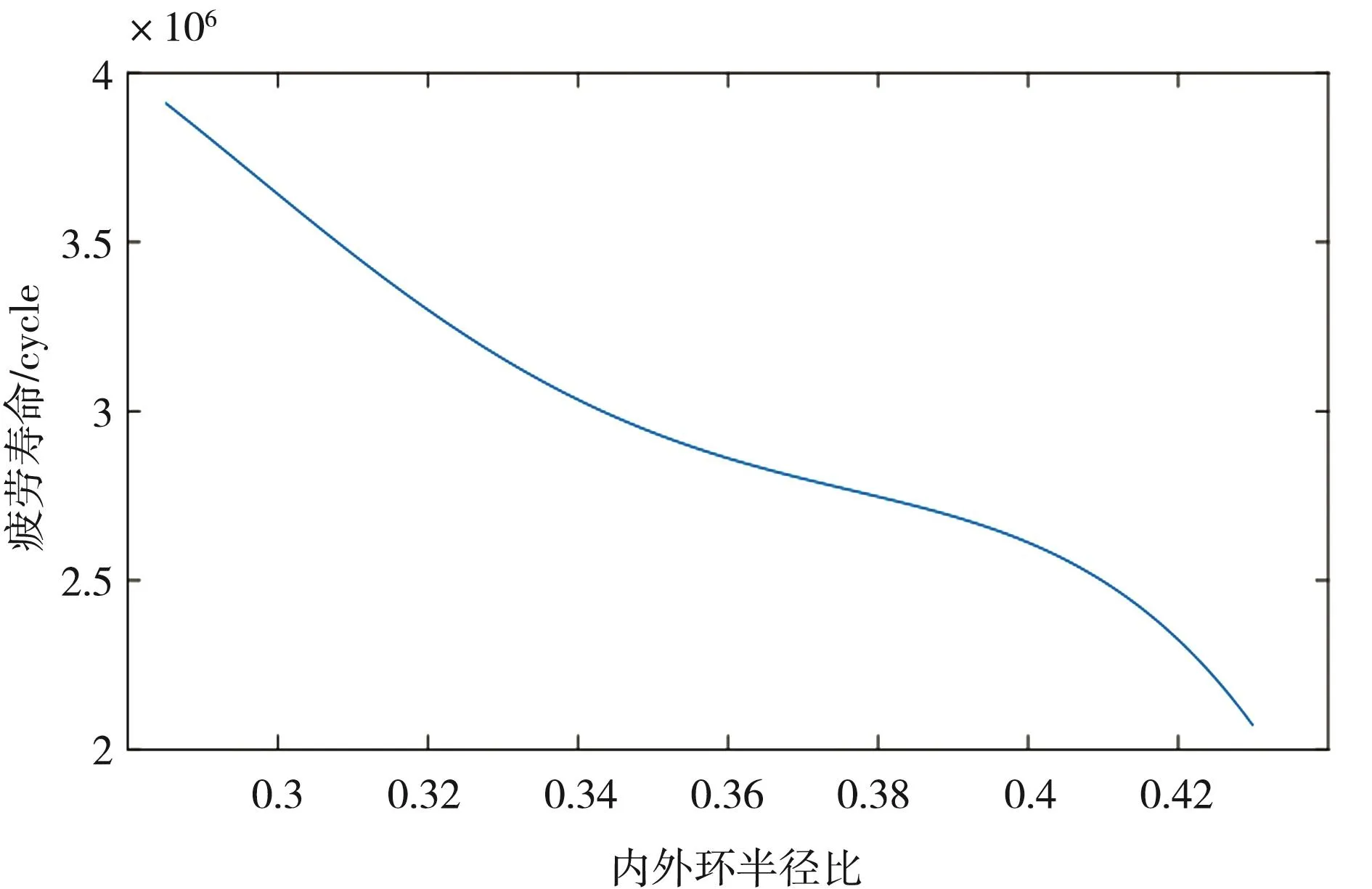
图7 疲劳寿命随内外环半径比变化图

从图7可以看出，随着内外环半径比的增加，滑环疲劳寿命将减小，且接近于线性变化。通过减小内外环半径比的方式可以获得较长使用寿命的“鹅颈”式滑环，但是受到FPC最小弯曲半径和转台通光孔径的限制，ε值不可以过小。

3.3 FPC导体层厚度h对滑环疲劳寿命N影响分析

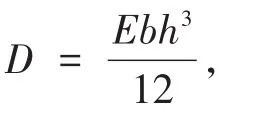
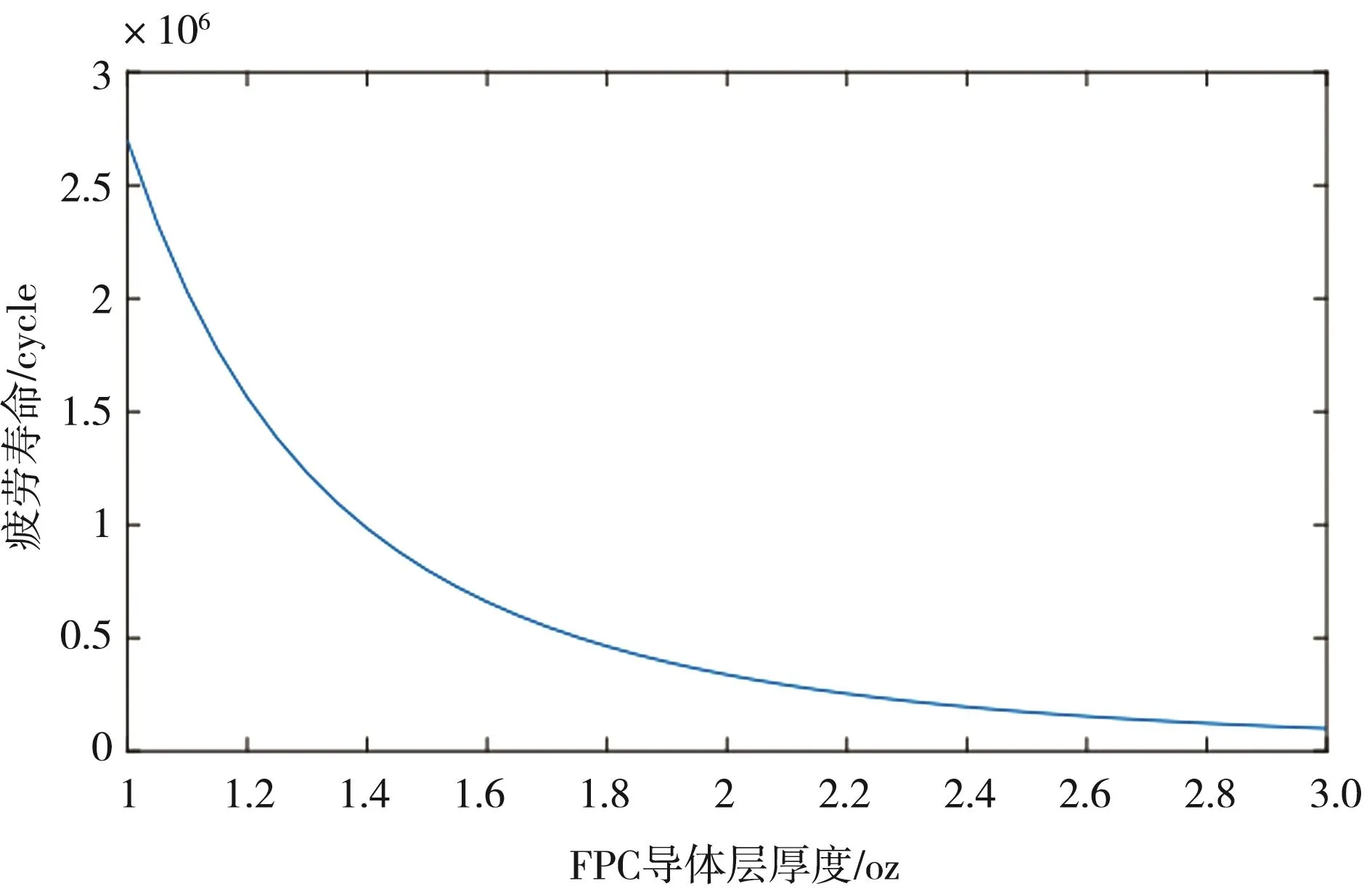
图8 疲劳寿命随导体层厚度变化图

4 滑环疲劳寿命验证

结合表1中的参数和FPC最小弯曲半径rmin取值范围的要求，取ε值为0.4，即滑环内环半径为40 mm，通光孔径为80 mm，代入寿命预估模型得到此时的Nφ=2.70E+06 cycles。设计寿命试验装置如图9所示，装置包括导电滑环样机、电源、电机驱动器、显示屏等。电机转速为10 r/min，试验行程为±0.5 rad，试验温度为（23±2）℃，相对湿度为（50±10）%，试验频率为4 Hz，试验失效准则参考IPC-TM-650 TEST METHODS MANUAL（2.4.3.1C）《铜箔的弯曲疲劳和延展性》。

图9 疲劳寿命试验装置

在试验进行前，要对FPC试样进行外观检查，试样表面应保证光滑、无皱折，废弃有工艺缺陷的试样；用内外环压板将FPC试样固定在内外环的侧壁上，为了防止试件受压失效，在压板与FPC之间放置垫片；压板固定装置在长时间工作时需牢固可靠，防止松动引起的试样滑动；调节滑环内外环，保证其与电机同轴，保证试验环境清洁，无冲击振动，满足试验温度和相对湿度的要求，测试滑环的7路通电性能。在试验过程中，每五个小时对试验现场进行检查，防止联轴器松动对滑环疲劳寿命产生影响。绘制FPC各路传输电阻值随循环加载次数的变化曲线，如图10所示。当任意一路传输电阻值变化范围超过10%时，计时器停止计数，读取此时显示屏上的循环加载次数，记为导电滑环的疲劳寿命N。如果FPC样品过早的出现失效，即该路加载次数较小，则去除该路，继续开展试验，直至FPC 7路全部失效。

图10 疲劳寿命试验结果

图10的试验结果表明，FPC初始电阻值为1.6 Ω，滑环在经过了2.66E+06 cycles往复回转后，FPC传输电阻值变化范围超过10%，电阻值达到1.76 Ω。根据判定准则，此时滑环失效，达到疲劳使用寿命，试验值略小于预估模型的理论计算结果，分析因为是滑环在工作过程中FPC导体层出现了脱胶，但是总体来说，误差在可接受范围5%以内，验证了模型的准确性，满足设计要求。

5 结论

FPC导体层断裂是“鹅颈”式有限转角导电滑环疲劳失效的主要影响因素。为了预估滑环的疲劳寿命，本文结合滑环运动规律，从导体层裂纹扩展能量的来源出发，基于能量法建立了滑环往复回转过程中的疲劳寿命预估模型。通过控制变量法，进一步分析滑环内环转动角度、内外环半径比和导体层厚度分别对滑环疲劳寿命的影响，综合考虑滑环的工作范围、FPC的通电能力和最小弯曲半径的要求，通常情况下，在满足静力安全时，可以通过减小滑环内外环半径比来增大滑环疲劳寿命，在需要大通光孔径的情况下可以减小导体层厚度来获得较长疲劳使用寿命的滑环。开展了滑环疲劳寿命试验，理论计算结果与试验结果相比误差为1.5%，在可接受范围内，证明了预估模型的准确性。受到试验条件的限制，本文未对上文论述的影响滑环疲劳寿命的三个因素进行试验，在接下来的研究中将会弥补这一不足。