SOME OSCILLATION CRITERIA FOR A CLASS OF HIGHER ORDER NONLINEAR DYNAMIC EQUATIONS WITH A DELAY ARGUMENT ON TIME SCALES∗

Xin WU(吴鑫)

School of Sciences,East China JiaoTong University,Nanchang 330013,China

E-mail:wuxin8710180@163.com

Abstract In this paper,we establish some oscillation criteria for higher order nonlinear delay dynamic equations of the formon an arbitrary time scale T with supT=∞,where n≥2,ϕ(u)=|u|γsgn(u)for γ>0,ri(1≤i≤n)are positive rd-continuous functions and h∈Crd(T,(0,∞)).The function τ∈Crd(T,T)satis fies τ(t)≤t andτ(t)=∞and f∈C(R,R).By using a generalized Riccati transformation,we give sufficient conditions under which every solution of this equation is either oscillatory or tends to zero.The obtained results are new for the corresponding higher order differential equations and difference equations.In the end,some applications and examples are provided to illustrate the importance of the main results.

Key words oscillation;nonlinear dynamic equations;higher order equation;delay dynamic equations;time scale

1 Introduction

During the past several decades,a great number of theoretical issues concerning dynamic equations on time scales have received considerable attention.Much of the focus has been on attempting to harmonize the oscillation theory for the continuous and the discrete,so the oscillation and nonoscillation of solutions of various equations has been investigated extensively;we refer the reader to the excellent monograph[3],the papers[1,7,9,10,20,23,30],and the references cited therein.Saker and Grace[21]studied the oscillation of the second-order quasilinear functional dynamic equation

and established some new sufficient conditions which ensure that every solution oscillates or converges to zero.Deng et al.[4]established some new oscillation criteria for second order delay dynamic equations

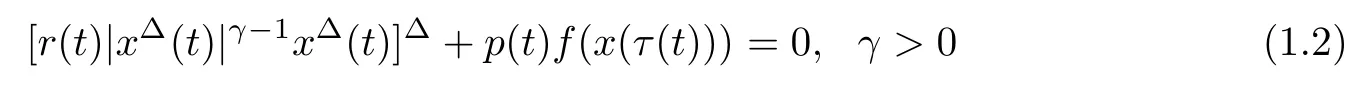
by means of the Riccati transformation technique.Zhou et al.[29]established necessary and sufficient conditions for the oscillation of second order strongly superlinear and strongly sublinear dynamic equations

Baculikova[2]considered the second order noncanonical differential equation with a delay argument

and established some sufficient conditions for the oscillation of(1.4).Karpuz[13]studied the asymptotic behaviour of the bounded solutions of a class of higher-order neutral dynamic equations

Recently,Hassan and Kong[12]discussed the new asymptotics and oscillation criteria for the nth-order nonlinear dynamic equation

with Laplacians and a deviating argument on a general time scale without any restrictions on g(t).For more results on dynamic equations,we refer the reader to the papers[6,8,11,14–17,22,24,26–28].

Motivated by the aforementioned classical works,in this paper,we shall investigate the higher order nonlinear delay dynamic equation

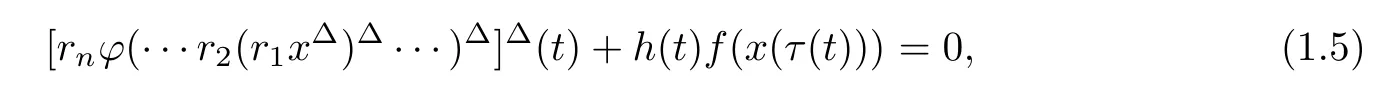
where ϕ(u)=|u|γsgn(u)for γ>0.Throughout this paper,we assume that T is an arbitrary time scale with supT=∞,and de fine the time scale interval[t0,∞)Tby[t0,∞)T:=[t0,∞)∩T.Furthermore,we assume that

The purpose of this paper is to establish some new oscillation criteria for a higher order nonlinear delay dynamic equation(1.5)under very mild conditions.Compared with(1.2),the investigation of higher order equation(1.5)is more complicated.To overcome the corresponding difficulties,we will employ the generalized Riccati technique.We would like to mention that the Riccati transformation plays an important role in the study of oscillatory behavior for(1.5).In short,the obtained results here improve and unify many known results on the topic.

The rest of this paper is organized as follows:in Section 2,we present our main results.In Section 3,we prove some useful lemmas and important estimates,which will be used in the proof of our main results.Later,we prove Theorems 2.1–2.3.In Section 4,we apply the oscillation criteria to different types of time scales to show that our results not only unify some of the known oscillation results for differential and difference equations,but can also be applied to other cases to determine oscillatory behavior.Finally,some examples are provided to illustrate the main results.

2 Main Results

For the convenience of our discussion,we de fine

where ϕ(u)=|u|γsgn(u)for γ>0.

A time scale T is an arbitrary nonempty closed subset of real numbers which have a topology inherited from the real numbers with the standard topology.For t∈T,we de fine the forward jump operator σ:T→T by σ(t):=inf{s∈T:s>t},while the backward jump operator ρ:T→T is de fined by ρ(t):=sup{s∈T:sinf T and ρ(t)=t.The graininess functionµ:T→[0,∞)is de fined byµ(t):=σ(t)−t.The function f:T→R is called right-dense continuous on T if it is continuous at right-dense points in T,and its left-sided limits exist at left-dense points in T.The set of all rd-continuous functions f are denoted by Crd(T,R).By a solution of(1.5),we mean a nontrivial real-valued function x∈([Tx,∞)T)with Tx≥t0,which has the property that Sk(t,x(t))∈([Tx,∞)T)for 0≤k≤n,and which satis fies(1.5)on[Tx,∞)T,whereis the space of differentiable functions whose derivative is rd-continuous.The solutions vanishing in some neighborhood of in finity will be excluded from our consideration.A solution x(t)of(1.5)is said to be oscillatory if it is neither eventually positive nor eventually negative;otherwise it is called nonoscillatory.For more details on time scales,we refer the reader to Bohner and Peterson[3].

For any t∈[t0,∞)T,we let

Given T∈[t0,∞)Tsufficiently large,for any t≥T,we de fine

and for any given function φ(t)>−1/rn(t)(t,T)such that rn(t)φ(t)is a∆-differentiable function,and a positive∆-differentiable function a(t),we assume that

and

Our main results on oscillation theorems for equation(1.5)can be stated as follows:

Theorem 2.1Suppose that either

holds.Furthermore,assume that there exist a function φ(t)satisfying φ(t)=0 for 0<γ<1,and a positive∆-differentiable function a(t),such that,for a sufficiently large T∈[t0,∞)T,

where T∗∈(T,∞)Tand d+(t):=max{d(t),0}.Then,

(i)every solution x(t)of(1.5)is oscillatory when n is odd;

(ii)every solution x(t)of equation(1.5)is either oscillatory orx(t)=0 when n is even.

For convenience,let Γ:={(t,s)∈T2:t0≤s≤σ(t),t,s∈[t0,∞)T}.For any function Q:T2→R,denote by QΔsthe partial derivative of Q(t,s)with respect to s.De fine

Theorem 2.2Assume that either(2.3)or(2.4)is satis fied.Furthermore,suppose that there exist a function φ(t)satisfying φ(t)=0 for 0<γ<1,a positive∆-differentiable function a(t)and Q∈X such that,for a sufficiently large T∈[t0,∞)T,

where T∗∈(T,∞)T.Then,

(i)every solution x(t)of(1.5)is oscillatory when n is odd;

(ii)every solution x(t)of equation(1.5)is either oscillatory orx(t)=0 when n is even.

In order to obtain more oscillation results for(1.5),as in[1],one can de fine another class of functions as follows:U∈Y if U∈→R and satis fies U(t,t)=0,t≥t0,U(t,s)>0,t>s≥t0.Using the function U,we establish a similar oscillation result as to that of Theorem 2.2.

Theorem 2.3Suppose that either(2.3)or(2.4)holds.Let U∈Y such that UΔs∈Crd(D,R)and UΔs≤0 on D,where D={(t,s):t≥s≥t0}.Furthermore,assume that there exist a function φ(t)satisfying φ(t)=0 for 0<γ<1,and a positive∆-differentiable function a(t)such that,for a sufficiently large T∈[t0,∞)T,

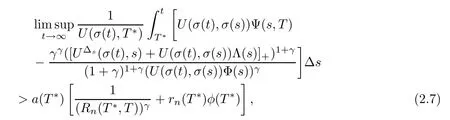
where T∗∈(T,∞)T.Then,

(i)every solution x(t)of(1.5)is oscillatory when n is odd;

(ii)every solution x(t)of equation(1.5)is either oscillatory orx(t)=0 when n is even.

Remark 2.4The results in this paper are expressed in a form with a high degree of generality.With an appropriate choice of the functions φ(t)and a(t)in Theorems 2.1–2.3,Q(t,s)in Theorem 2.2 and U(t,s)in Theorem 2.3,we can see that[25,Theorems 3.1–3.2]are special cases of Theorem 2.2–2.3.

Remark 2.5To conclude this section,we propose the following open problem:fi nd sufficient conditions for every solution of(1.5)to be oscillatory when n is even.

3 The Proof of Main Results

3.1 Some useful lemmas

It is easy to prove the following lemma(see also Sun et al.[22,Lemma 2.1]):.

Lemma 3.1Let 1≤µ≤n.Then,

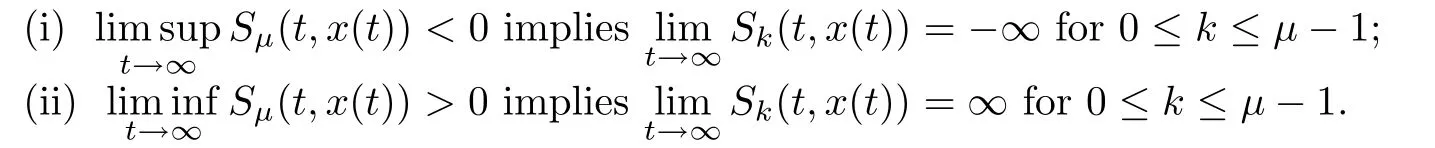
Lemma 3.2Let x(t)be an eventually positive solution of equation(1.5).Then there exist a T∈[t0,∞)Tand an integer 0≤κ≤n with n+κ being even such that

(i)κ≤n−1 implies(−1)κ+iSi(t,x(t))>0 on[T,∞)Tfor any κ≤i≤n−1;

(ii)κ>0 implies Si(t,x(t))>0 on[T,∞)Tfor any 0≤i≤κ−1.

ProofSupposing that x(t)is an eventually positive solution of equation(1.5),there exists t1∈[t0,∞)Tsuch that x(t)>0 and x(τ(t))>0 on[t1,∞)T.In a fashion similar to the proof of[26,Lemma 2.2],it is not difficult to obtain the desired results.

Lemma 3.3Assume that(2.3)or(2.4)holds.Let x(t)be an eventually positive solution of equation(1.5).Then there exists T∈[t0,∞)Tsufficiently large such that Sn(t,x(t))>0 for any t∈[T,∞)T.Moreover,

holds when n is odd and either(3.1)holds or=0 when n is even.

ProofSince x(t)is an eventually positive solution of equation(1.5),that is,there exists t1∈[t0,∞)Tsuch that x(t)>0 and x(τ(t))>0 on[t1,∞)T,it follows from Lemma 3.2 that there exists an integer 0≤κ≤n satisfying that κ+n is even such that(−1)κ+iSi(t,x(t))>0 for t∈[t1,∞)Tand κ≤i≤n.

When n is odd,κ must be an odd integer and xΔ(t)=S1(t,x(t))/r1(t)>0 for t∈[t1,∞)T.Consequently,

In this case,we claim that κ=n.If we were to assume that this is not the case,then we would have Sn−1(t,x(t))<0 and Sn−2(t,x(t))>0 for t∈[t1,∞)T.By(3.2),it is not difficult to get that there exists t2∈[t1,∞)Tand a constant c>0 such that x(τ(t))≥c on[t2,∞)T.From(1.5),we have

on[t2,∞)T.If(2.3)holds,integrating the above inequality from t2to t,we obtain that for t∈[t2,∞)T,

This is in contradiction to the fact that Sn(t,x(t))>0 for t∈[t1,∞)T.Thus,κ=n,and(3.2)holds.

If(2.4)holds,integrating(3.3)from t to∞,we get that,for t∈[t2,∞)T,

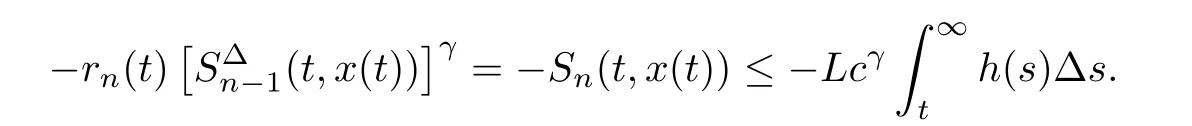
Then,it follows from Sn−1(t,x(t))<0 that

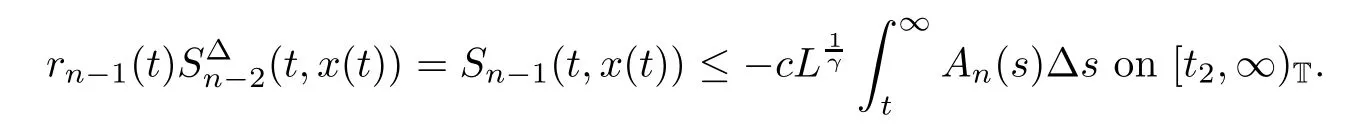
Again,integrating the above inequality from t2to t,we conclude from Sn−1(t,x(t))>0 that

which is in contradiction to the fact that Sn−2(t,x(t))>0 on[t1,∞)T.Hence,κ=n,and(3.2)holds.

When n is even,we infer from Lemma 3.2 that κ is an even integer.Thus,S1(t,x(t))>0 or S1(t,x(t))<0,which indicates thatx(t)≥0.We claim thatx(t)0 implies that κ=n.By a similar argument as to that above,we get a result that is in contradiction to(2.3)or(2.4).This ends the proof.

Lemma 3.4Assume that either(2.3)or(2.4)holds.Let x(t)be a solution of equation(1.5)satisfying(3.1)for t∈[T,∞)Twith some T∈[t0,∞)T.Then,for t∈[T,∞)T,we getand

ProofWithout loss of generality,we can assume that T is sufficiently large such that x(τ(t))>0 on[T,∞)T.By(1.5),it is obvious that Sn(t,x(t))is decreasing on[T,∞)T.Then it follows that,for t∈[T,∞)T,

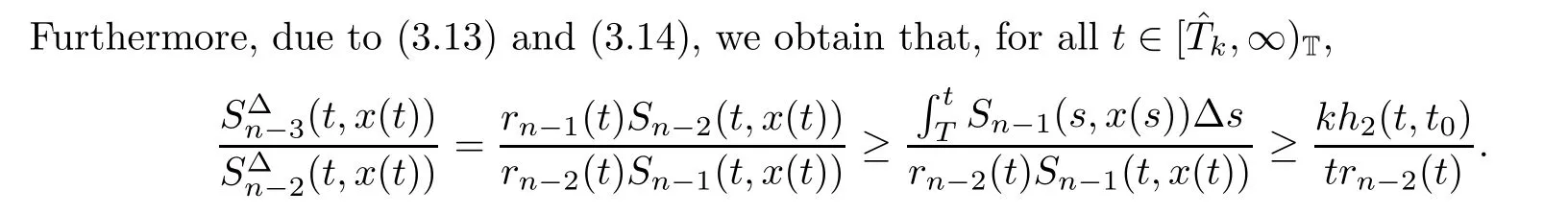
This finishes the proof.

Lemma 3.10Assume that either(2.3)or(2.4)holds.Let x(t)be a solution of equation(1.5)satisfying(3.1)for t∈[T,∞)Twith some T∈[t0,∞)T.Then,this satis fies that

3.2 Proof of Theorem 2.1

Suppose that equation(1.5)has a nonoscillatory solution x(t)on[t0,∞)T.Without loss of generality,we may assume that x(t)is eventually positive.Then,there is a sufficiently large T∈[t0,∞)Tsuch that x(t)>0 and x(τ(t))>0 on[T,∞)T.Moreover,by Lemma 3.3,(3.1)holds.

When n is odd,we de fine a generalized Riccati substitution as follows:

3.3 Proof of Theorem 2.2

Suppose that equation(1.5)has a nonoscillatory solution x(t)on[t0,∞)T.Without loss of generality,we may assume that x(t)is eventually positive.Then there is a sufficiently large T∈[t0,∞)Tsuch that x(t)>0 and x(τ(t))>0 on[T,∞)T.Moreover,by Lemma 3.3,(3.1)holds.

When n is odd,we proceed as in the proof of Theorem 2.1 to obtain that

Multiplying both sides of(3.24)with t replaced by s,by Q(σ(t),σ(s))and integrating with respect to s from T∗to t,where t∈[T∗,∞)Twith T∗∈(T0,∞)T,one gets

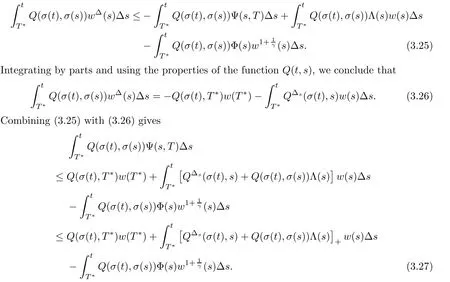
By dividing Q(σ(t),T∗)and taking the limsup on both sides as t→∞,we obtain a contradiction to(2.6).Therefore,every solution x(t)of(1.5)is oscillatory.

When n is even,we can derive from Lemma 3.3 that either(3.1)holds orx(t)=0.If(3.1)holds,then we can show that equation(1.5)is oscillatory,and hence omit its proof.This completes the proof of Theorem 2.2.

3.4 Proof of Theorem 2.3

Suppose that equation(1.5)has a nonoscillatory solution x(t)on[t0,∞)T.Without loss of generality,we may assume that x(t)is eventually positive.Then there is a sufficiently large T∈[t0,∞)Tsuch that x(t)>0 and x(τ(t))>0 on[T,∞)T.Moreover,by Lemma 3.3,(3.1)holds.

When n is odd,we proceed as in the proof of Theorem 2.1 to obtain(3.24).Then,from(3.24),we obtain that

for all s∈[T0,∞)T.Multiplying both sides of the above inequality by U(σ(t),σ(s))and integrating with respect to s from T∗to σ(t),where σ(t)∈[T∗,∞)Twith T∗∈(T0,∞)T,we get

In view of(3.29),(3.30)and U(σ(t),σ(t))=0,we conclude that

which contradicts(2.7).Hence,every solution x(t)of(1.5)is oscillatory.

When n is even,we infer from Lemma 3.3 that either(3.1)holds orx(t)=0.If(3.1)holds,then we see that equation(1.5)is oscillatory.We omit the details.This completes the proof.

4 Applications on Particular Time Scales

In this section,we apply Theorems 2.1–2.3 to different types of time scales.We start with the case of when T=R,and(1.5)becomes the nonlinear delay differential equation

Applying Theorems 2.1–2.3 to equation(4.1),we get the following results:

Corollary 4.1Suppose that either

(i)every solution x(t)of(4.1)is oscillatory when n is odd;

(ii)every solution x(t)of equation(4.1)is either oscillatory orx(t)=0 when n is even.

Corollary 4.2Suppose that either the condition(4.2)or the condition(4.3)holds.Let U∈Y such that,where D={(t,s):t≥s≥t0}.Furthermore,assume that there exist a function φ(t)satisfying φ(t)=0 for 0<γ<1,and a positive differentiable function a(t)such that for a sufficiently large T∈[t0,∞)R,

where T∗∈(T,∞)R.Then,

(i)every solution x(t)of(4.1)is oscillatory when n is odd;

(ii)every solution x(t)of equation(4.1)is either oscillatory orx(t)=0 when n is even.

Then we have,from Theorems 2.1–2.3,the following oscillation results for equation(4.4):

Corollary 4.3Suppose that either

holds.Furthermore,assume that there exist a sequence φ(t)satisfying φ(t)=0 for 0<γ<1,and a positive sequence a(t),such that,for a sufficiently large N∈N,

where N∗>N.Then,

(i)every solution x(t)of(4.4)is oscillatory when n is odd;

(ii)every solution x(t)of equation(4.4)is either oscillatory orx(t)=0 when n is even.

Corollary 4.4Assume that either(4.5)or(4.6)is satis fied.Furthermore,assume that there exist a sequence φ(t)satisfying φ(t)=0 for 0<γ<1,a positive sequence a(t)and Q∈X such that,for a sufficiently large N∈N,

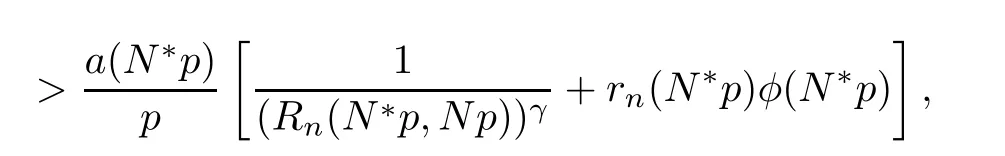
where Θ1(n,k)=[∆ps((n+1)p,kp)+Q((n+1)p,(k+1)p)Λ(kp)]+and N∗>N.Then,

(i)every solution x(t)of(4.4)is oscillatory when n is odd;

(ii)every solution x(t)of equation(4.4)is either oscillatory orx(t)=0 when n is even.

Corollary 4.5Suppose that either(4.5)or(4.6)holds.Let U∈Y such that∆psU≤0 on D,where D={(n,k):n≥k≥n0}.Furthermore,assume that there exist a sequence φ(t)satisfying φ(t)=0 for 0<γ<1,and a positive sequence a(t)such that for a sufficiently large N∈N,

Now,we give our oscillation results for(4.7).

Corollary 4.6Suppose that either

holds.Furthermore,assume that there exist a sequence φ(t)satisfying φ(t)=0 for 0<γ<1,and a positive sequence a(t),such that,for a sufficiently large N∈N,

where N∗>N.Then,

(i)every solution x(t)of(4.7)is oscillatory when n is odd;

(ii)every solution x(t)of equation(4.7)is either oscillatory orx(t)=0 when n is even.

Corollary 4.7Assume that either(4.8)or(4.9)is satis fied.Furthermore,assume that there exist a sequence φ(t)satisfying φ(t)=0 for 0<γ<1,a positive sequence a(t)and Q∈X such that,for a sufficiently large N∈N,

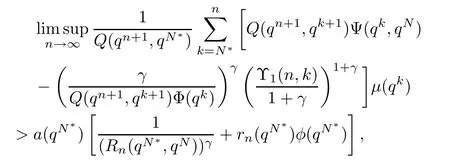
where Υ1(n,k)=[(qn+1,qk)+Q(qn+1,qk+1)Λ(qk)]+and N∗>N.Then,

(i)every solution x(t)of(4.7)is oscillatory when n is odd;

(ii)every solution x(t)of equation(4.7)is either oscillatory orx(t)=0 when n is even.

Corollary 4.8Suppose that either(4.8)or(4.9)holds.Let U∈Y such that∆qsU≤0 on D,where D={(n,k):n≥k≥n0}.Furthermore,assume that there exist a sequence φ(t)satisfying φ(t)=0 for 0<γ<1,and a positive sequence a(t)such that,for a sufficiently large N∈N,

where Υ2(n,k)=and N∗>N.Then,

(i)every solution x(t)of(4.7)is oscillatory when n is odd;

(ii)every solution x(t)of equation(4.7)is either oscillatory orx(t)=0 when n is even.

5 Numerical Examples

Example 5.1Let p,L,γ be positive constants,let 0<γ<1,and let the time scale be T=pZ.Consider the dynamic equation

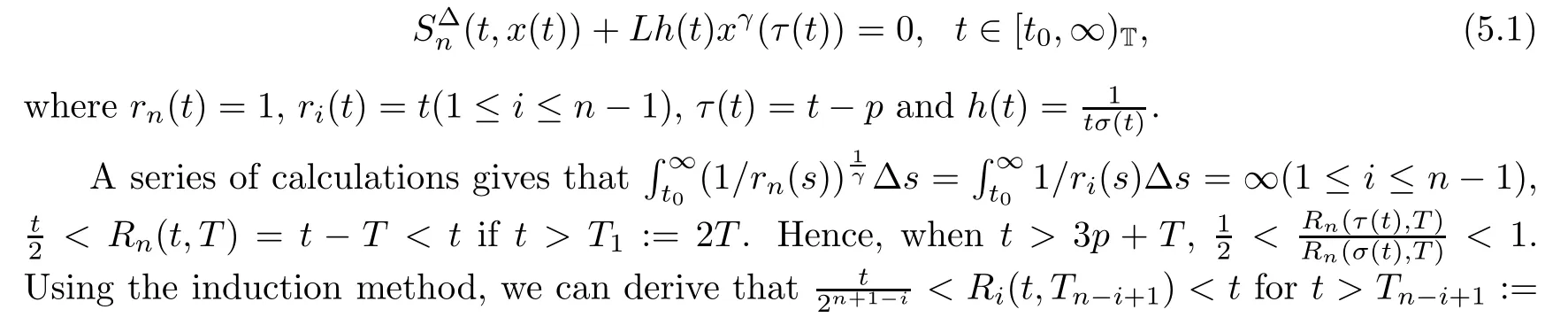
By Theorem 2.2,every solution x(t)of(5.2)is oscillatory when n is odd,and every solution x(t)of equation(5.1)is either oscillatory orx(t)=0 when n is even.