基于Dijkstra算法的城市物流公交系统优化

王树梅，黄 石，臧禹顺

(1.江苏师范大学 计算机科学与技术学院，江苏 徐州 221116; 2.山东三四物流服务有限公司，山东 单县 274300)

0 引 言

随着国家的产业升级，城镇化建设，三四线城市逐渐成为生产基地和相对集中的生活中心，每天需要消耗大量的生产资料和生活资料，而产成品又要不断地运到全国各地，因此对物流运输服务提出了更高的需求。另一方面，国内物流行业生产力过于分散，最大的物流公司业务占比不到4%的全国物流份额，运输车辆空返率高，物流行业信息化水平差，除了一些快递公司的信息化水平基本满足客户需求外，普通的物流公司大多数还是处于手工记录单据的状态。

基于以上问题，许多专家提出了诸多物流路径优化算法[1-9]。文献[10]提出了基于蚁群算法的物流配送路径优化算法，以成本最小化和最大限度减少碳排放量构建了一种路径规划多目标优化模型。文献[11]针对冷链配送时效性强的特性问题，建立冷链配送路径多目标优化模型，运用遗传算法对模型进行求解。文献[12]针对物流领域降低配送成本、提升配送效率的需求，通过数学建模的方式，将物流路径优化问题转化为数学研究领域经典的旅行商问题。文献[13]结合客户的消费行为将客户分为多个层级，根据每层级客户的特点设置超时惩罚成本，构建出基于客户分类的即时配送路径优化模型。文献[14]针对航空物流领域对路径进行精确计算以降低配送成本的需求，对路径的优化方法进行了研究。文献[15]提出了基于A*算法的民航物流运输路径优化算法，实现了民航物流路径的最优规划。

文中提出了基于移动互联网的信息化平台的物流公交优化算法，通过该平台实现社会物流的信息共享，资源整合，使同一流向的货物能够共享运力，提高整体社会物流的效率。为了实现这一信息平台，在始端的发货接货和末端的送货收货，就成为非常关键的环节。在整个平台中，城市物流公交模块就是为了解决物流系统的两端而设计开发的，该模块处于对整个社会物流信息的收集及整合的始端，能高效地处理这些数据尤为重要。

1 最短路径问题

交通运输网络可以表示为一个带权图，用图的顶点表示城市，用图的边表示城市之间的交通运输路线，各边的权值表示该路线的长度或沿此路线运输所需要的时间或运费等。传统意义上的单源最短路径问题是基于有向带权图所表示的交通网络，文中对此算法稍作修改，可以适用于带权无向连通图，且在参数里设置了起点和终点，函数返回两点之间的最短距离。根据修改后的最短路径算法，输入任意两个顶点的信息即可求出它们之间的最短距离或者最小代价。

数据结构[16]上也有一多源多目标FLOYD算法，这个算法通过两个循环嵌套将所有顶点之间的最短路径计算出来，这个算法的时间复杂度为O(n3)，算法效率较低。这个算法也可以满足文中物流最短路径的需求，但事实上物流最短路径需要的是当前两个城市之间的最短路径，不需要将其他所有城市的最短路径都求出来。因此，文中对Dijkstra算法进行修改，图是带权无向连通图，权是城市之间的距离，输入图中任意两个顶点，输出两个顶点的最短距离以及最短路径。具体步骤如下：

给定带权连通无向图Graph(V,E)，v和k是图G的两个顶点，下面是求图G中v和k之间的最短路径算法Dijkstra(G,v,k)。

(1)初始时，顶点集合S只包含顶点v，即S={v},v到自己的距离为0。顶点集合U包含除v以外的其他顶点，k在集合U中，v到U中各顶点的距离为边上的权(若顶点之间 有边)或∞(顶点之间无边)。

(2)从U中选取一个顶点u，它是v到U中距离最小的一个顶点，然后把顶点u加入到S中。

(3)以顶点u为新考虑的中间点，修改v到U中各顶点j(j∈U)的距离，若从v到j经过u的距离(图1中为cvu+wuj)比原来不经过顶点u的距离(图1中为cvj)更短，则修改v到j的最短距离值(图1中修改为cvu+wuj)。

(4)判断j==k，如果是则循环退出，v到k的最短路径即求出，否则转(2)。

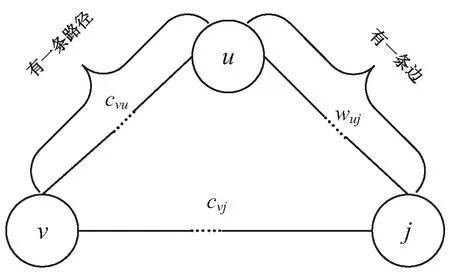
图1 顶点v到顶点j的路径比较

伪代码描述如下：

(1)初始化：S←{v}；

dist[j]←Edge[v][j]，j为除v以外的其他顶点,j∈V-S;

Edge[][]为图G的邻接矩阵。

(2)求出最短路径的长度：dist[u]←min{dist[j]}，j∈V-S;

S←S∪{u};

(3)修改：dist[j]←{dist[j],dist[u]+Edge[u][j]}，对于每一个j∈V-S;

(4)判断：若j=k，则算法结束，否则转(2).

2 城市物流公交优化算法

城市物流公交是将位于不同城市的物流信息进行共享，物流资源进行优化使用，达到节约成本的目的。本模块算法包括两个部分，分别是货车分配和货车回收。

2.1 货车分配问题

货车分配问题分为三种情况，一是所有货车Ti(1≤i≤n)和货物G都在同一个城市，根据现有货车的可载重量和可载体积进行资源利用最大化分配送货车。二是货车分散在不同的城市，货物在其中一个城市，在这种情况下除了考虑货车的可载重量和可载体积以外，还要将货车送货的距离考虑在内。三是货车分布在不同城市，货物也分布在不同城市，这是一种比较复杂的情况，在重量和体积都满足的前提下，距离近的货车优先被选中。

这里引入一个利用率(UR)的概念，货车利用率的计算与货车可载重量(TW)、货车可载体积(TV)、货物可载重量(GW)和货物可载体积(GV)都有关系。在货车体积和重量都满足的前提下，计算货车的利用率。在计算货车利用率之前，需要先判断体积是否满足条件，若不满足则此车排除，若满足则再判断重量是否满足，若满足则计算该车利用率，否则排除该车。在计算每辆货车的UR之前，需要判断货车的状态，设其状态值为1时货车在用，状态值为0时货车空闲。

(1)

(1)货车分配问题一。

这种情况是比较简单的一种，货车和货物均在同一城市，需要计算各个货车利用率，选取利用率最大的货车即可。如图2所示，UR1,UR2,…,URn分别为货车T1,T2,…,Tn根据式(1)计算出来的利用率，当体积或重量不满足条件时，利用率为0。

URmax=MAX{UR1,UR2,…,URn}

(2)

设Ti的利用率最大，则第i辆货车被选中作为送货车送货。

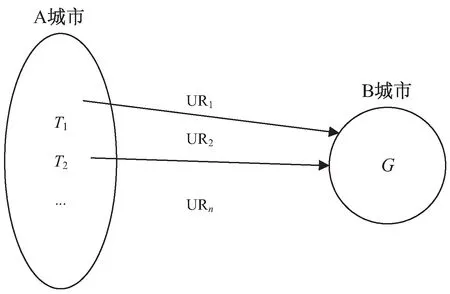
图2 货车分配问题一模型

(2)货车分配问题二。

当货车分散在不同的城市，货物与货车也不在同一个城市，如何选取货车进行送货。这类问题模型如图3所示。这种情况下不但要考虑货车可载体积和重量，也即是货车利用率，还要考虑送货距离。这里设定，当利用率都大于0时，按照距离远近优先选取货车。

图3 货车分配问题二模型

货车T1,T2,…,Tn分别在A1,A2,…,An城市，货物G在B城市，需要送到C城市。现在从T1,T2,…,Tn中选取一辆货车进行送货，货车选取步骤如下：

①当货车状态值为0时，根据式(1)货物的重量和体积计算出每辆货车的利用率UR1,UR2,…,URn；

②在所有利用率UR中挑选出利用率大于0的货车Tk1,Tk2,…,Tkm；

③利用式(4)计算货车Tk1,Tk2,…,Tkm到货物的最短路径距离Dk1,Dk2,…,Dkm；

④在Dk1,Dk2,…,Dkm中找出最小值对应的货车Tp即为最终选车结果。

设Tk1,Tk2,…,Tkm的利用率大于0，在计算货车和货物之间的距离时，利用改进后的Dijkstra算法求出各个货车到货物的最短路径长度Dk1,Dk2,…,Dkm。

Dmin=MIN{Dk1,Dk2,…,Dkm}

(3)

Dki=Dijkstra(G,Aki,B)

(4)

(3)货车分配问题三。

这种情况下货车和货物都在不同的城市，如何给每一个货物分配到最合适的货车。这种问题模型如图4所示。这是一种比较复杂的情况，这里采取的方案先构造利用率矩阵，在矩阵中寻找利用率大于0的货车，再在这些货车中计算最小路径矩阵，具体步骤如下:

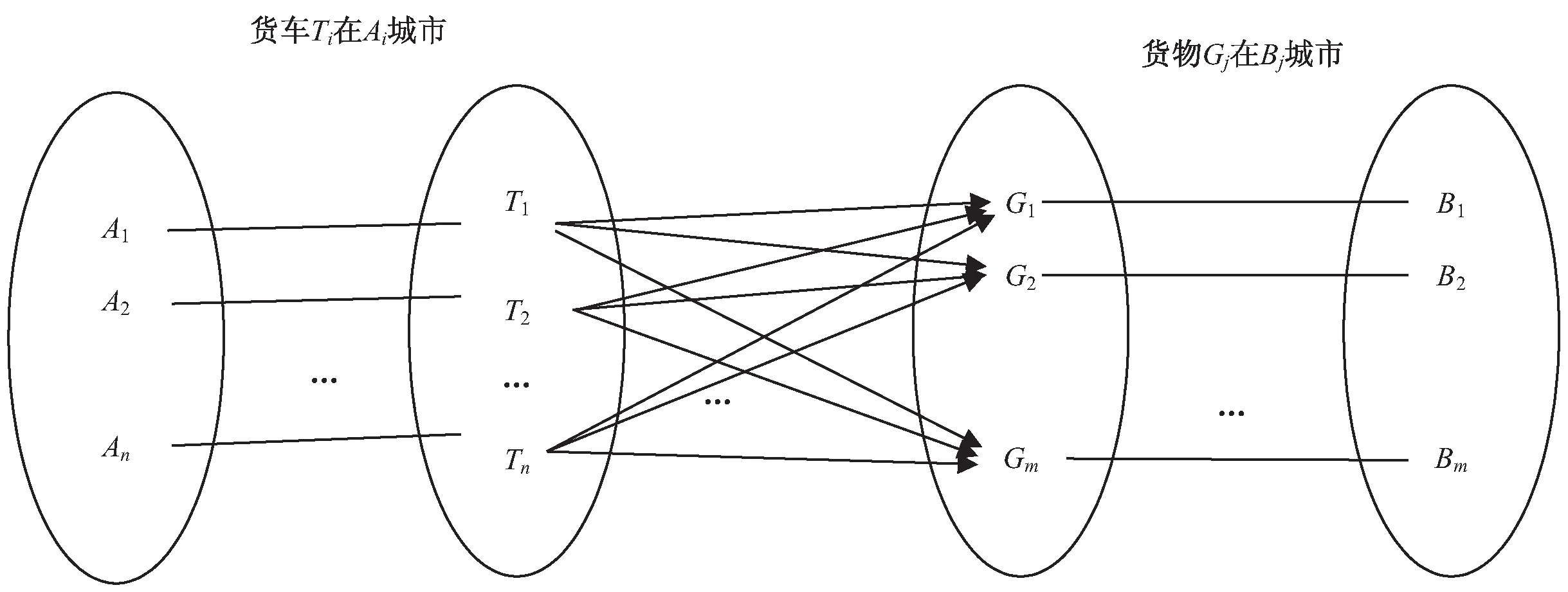
图4 货车分配问题三模型

①当货车状态为空闲时，即其状态值为0，根据式(1)计算利用率矩阵UMn*m，其中URij为货车Ti(1≤i≤n)与货物Gj(1≤j≤m)之间的利用率。

(5)

② If(URij>0)，计算Dij(Dij为Ai到Bj的最短路径长度)，否则，Dij=∞，得到矩阵Dn*m：

(6)

③计算矩阵Dn*m的第j列的最小值：MDj=MIN{Dij,1≤i≤n} =Dpj，则给货车Tp分配的货物是Gj。最短路径长度最小值向量为：

MD={MD1,MD2,…,MDm}

(7)

式(7)的结果为不同地点的n辆货车m个货物的最终分配结果，这种结果的前提是首先考虑距离，其次考虑利用率。

2.2 货车回收问题

系统里货车信息包括货车的编号、可载重量、可载体积、出发地、目的地和状态，货车在使用过程中，这些关键字的值都会发生变化，状态值为1。使用完毕需要在系统里对货车信息进行初始化，也即是货车的回收，将货车的状态值State改为0，可载重量TW和可载体积TV改为初始值。这里需要注意的是，为了提高货车的利用率UR，回收货车时，将其目的地End改为出发地Start，这样避免了货车跑空车，就可以在目的地再次为货车分配货源，提高了货车的使用率。货车的回收过程如图5所示。

图5 货车回收过程示意图

3 实验数据分析

以图6城市物流交通网络示意图为例，测试以下货车分配和回收算法。货车1-4的可载重量分别是6吨、11吨、15吨和19吨，可载体积分别是15方、30方、40方和50方。货物1-3的重量分别是10吨、15吨和5吨，体积分别为25方、30方和13方。

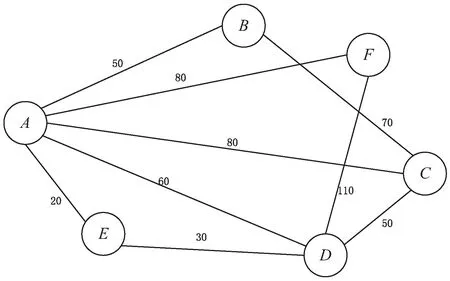
图6 城市物流交通网络示意图

(1)货车分配问题一。

货车1、货车2、货车3和货物1均在A城市，现在从三辆货车里选出一辆运送货物1。这种情况只需计算三辆车相对货物的利用率，选择利用率最大的车。三辆车的利用率分别是0、1.74和1.29，利用率最大的是货车2，所以对货物1分配的车是货车2。

(2)货车分配问题二。

货车1、货车2、货车3和货物1分别在A、B、C、D城市，从三辆货车里选出一辆运送货物1。三辆车的利用率分别是0、1.74、1.29，也即是只有货车2和货车3满足运送货物1的条件，而货车2和货车3距离货物1的最短距离分别是170公里和200公里，选择距离最近的货车，因此分配货车2运送货物1。

(3)货车分配问题三。

表1是货车初始化数据，A B C D E F表示6个不同位置的城市。货车1初始载重量为10吨，可载体积为12方，所在地是A城市。货车2初始载重量为20吨，可载体积为35方，所在地是B城市。货车3初始载重量为15吨，可载体积为21方，所在地是C城市。货车4初始载重量为30吨，可载体积为35方，所在地是D城市。

现在货物1在E城市，利用式(1)分别计算出各个货车相对货物1的利用率，分别是0、1.74、1.29、1.02，也即是货车2-4都满足条件。再采用Dijkstra算法计算出货车2-4至货物1的最短距离，分别是70公里、90公里和30公里。综合利用率和距离数据，在利用率都满足条件的前提下，选择距离最近的货车，因此选择货车4作为运送货物1的车。货车4被选上后，修改其使用状态为1，并且再计算其他货物的利用率时自动为0，距离自动为∞。

货物2在F城市，重量是15吨，体积是30方，需要分配货车。由于货车4已被分配给货物1，所以在剩下的三辆车里进行选择。货车1、货车2和货车3相对货物2的利用率分别是0、0和1.75，从利用率上看只有货车3满足条件，选择利用率大于0的货车3作为运送货物2的车，修改货车3的使用状态为1。

货物3在E城市，重量是5吨，体积是13方。由于货车3和货车4已分配出去，剩下货车1和货车2。货车1和货车2相对货物3的利用率分别是1.70和0.88，最短距离是20公里和70公里。货车1的利用率较大，而且距离货物3最近，所以选择货车1作为运送货物3的车。货车1、3、4被分配后各项数据改变如表2所示。

表1 货车初始化数据

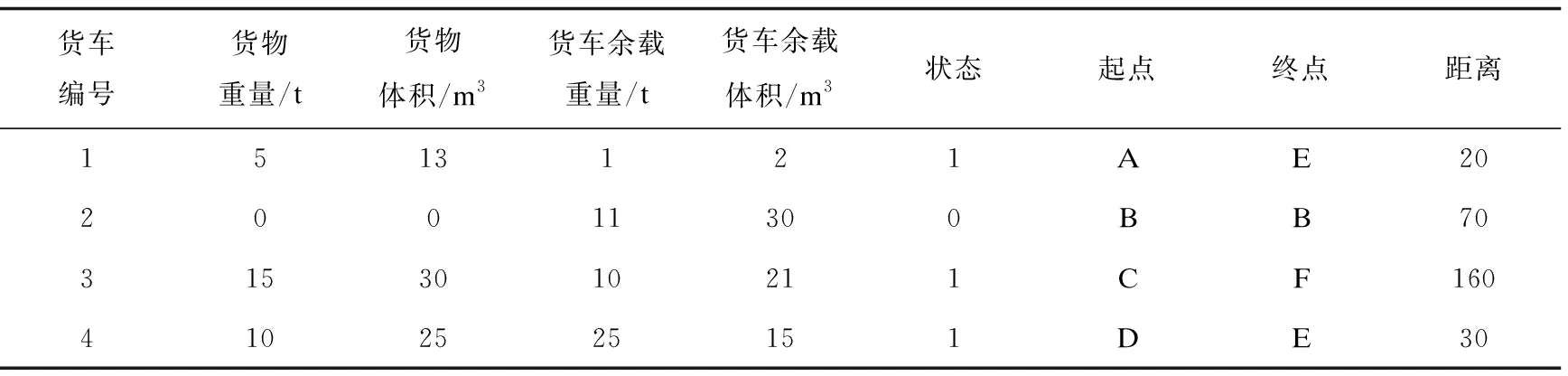
表2 货车分配后的数据

(4)货车回收。

对表2中的货车1、3、4进行回收，经确认货物已送达目的地后，对三辆车进行回收，回收后的各辆货车各项数据进行修改。修改后的数据如表3所示，货车1、3、4的可载重量恢复到初始状态，货车使用状态值均改为0，起点和终点均是各辆货车送达货物的城市，距离也初始化为0。通过对货车的回收，可以使货车及时被再次使用。

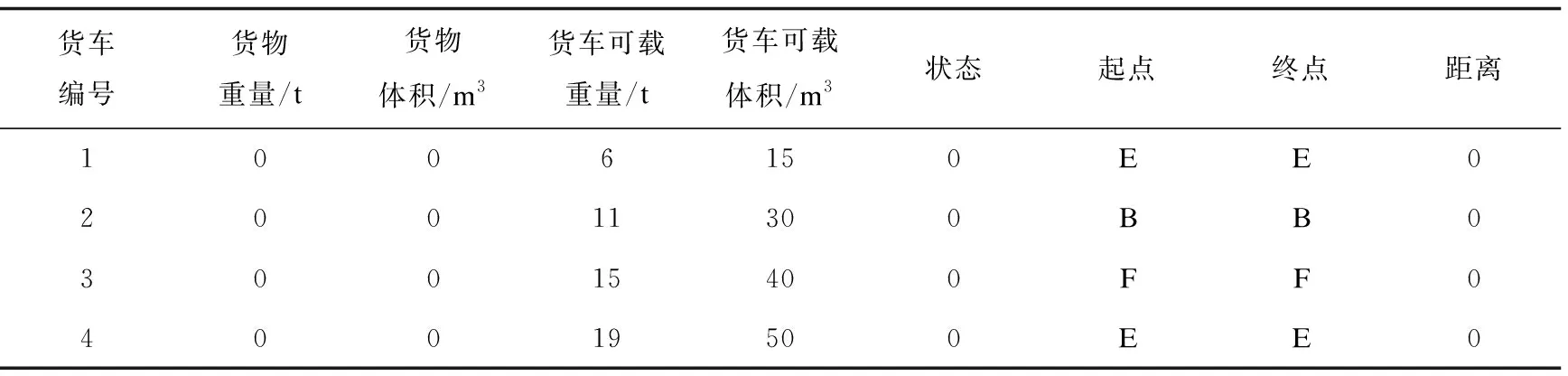
表3 货车回收后的数据

4 结束语

在移动互联网背景下，为了提高物流效率，充分利用物流运输资源，提出了本算法。通过实验数据可以看出，该算法在同地多车一货、同地多车和异地一货、异地多车多货三个货车分配问题上实现了利用率和距离的优化。在系统的接收端，对货车的及时回收和再使用在货车回收算法中得到了实现。在后面的研发过程中，会继续优化发送端和接收端之间的协调和优化，提高平台的使用效率。