钢束对空心板桥梁横向分布系数的影响

魏保平

（中国中元国际工程有限公司，北京市 100089）

0 引言

目前计算空心板的横向分布系数常用的方法包括：（1）利用桥博横向分布计算模块计算；（2）基于通用有限元软件建立梁格模型，通过每片梁的挠度反算各片主梁的横向分布系数。方法（2）的通用性强于方法（1），但建模工作量较大。方法（2）中，在计算每片主梁的挠度过程中，可以考虑板梁预应力束等因素对其竖向刚度的影响，得出更细分的挠度值和分布系数值。常规的结构设计过程中，一般不考虑板梁预应力束对其横向分布系数的影响。鉴于预应力束会提高板梁的竖向刚度，文中以一座简支空心板梁桥为例，对空心板的不同配束情况，通过梁格法得到的跨中位移计算出横向分布系数，并与桥博中铰接板梁法计算的结果进行校核，以研究预应力束对其横向分布系数的影响。

1 工程概况

某桥简支空心板梁预制梁长为15.96 m，计算跨径为15.46 m，梁高0.8 m，边梁梁宽1.95 m，中梁梁宽1.24 m，梁间现浇湿接缝宽0.1 m，桥面宽25.25 m，桥面布置为1.25 m（给水管道）+4.5 m（人行道）+7.5 m（机动车道）+7.5 m（机动车道）+ 4.5 m（人行道）。由2 片边梁、17 片中梁和18 道现浇纵向湿接缝组成。预制和现浇结构均采用C50 混凝土，预应力钢束采用标准强度为fpk=1 860 MPa 的钢绞线。空心板梁截面构造如图1、图2 所示（仅示意跨中截面）。

图1 中板跨中截面（单位：mm）

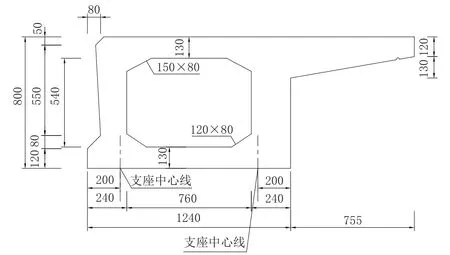
图2 边板跨中截面（单位：mm）

2 使用桥博进行横向分布系数的求解

首先采用桥博软件中的“横向分析”计算功能对本桥按“铰接板梁法”进行横向分布系数的求解。采用Midas Civil 中自带的“截面特性计算器”计算各截面的抗弯刚度和抗扭刚度。

考虑车道折减会影响各主梁的横向分布情况，故分别求得多车道汽车横向分布系数，见表1（考虑车道折减系数）。可以看到，在考虑车道折减系数的情况下，车道数越多，其横向分布不一定越大。这在设计中值得注意。另外，1 号边板的横向分布系数值小于19 号边板，是由1 号边板其上布置有管架，车道荷载离其较远所致。

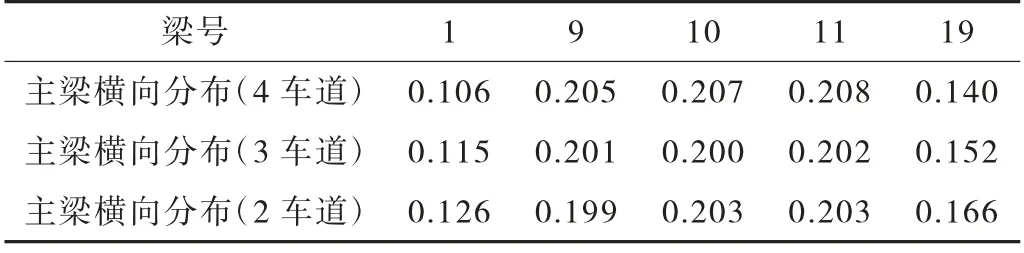
表1 桥博计算横向分布系数

3 建立梁格分析模型

基于Midas Civil 建立该简支空心板梁的空间梁格等效分析模型，19 片纵梁模拟成纵向梁单元，18道纵向湿接缝通过虚拟横梁连接，并释放横梁梁端约束。本文考虑以下3 种空心板钢束布置情况（钢束形状参照公路桥涵通用16 m 空心板）：

（1）边板2 根3*Φ15.2 和2 根4*Φ15.2，中板4根3*Φ15.2（以下简称“钢束1”）。

（2）边板4 根4*Φ15.2，中板2 根3*Φ15.2 和2根4*Φ15.2（以下简称“钢束2”）。

（3）边板2 根4*Φ15.2 和2 根5*Φ15.2，中板4根4*Φ15.2（以下简称“钢束3”）。

全桥工划分991 个节点和1 222 个单元，等效分析空间梁格模型如图3 所示。

图3 空心板梁模型

4 梁格模型横向分布系数求解

为方便与桥博计算结果进行比较，本模型仅考虑4 车道作用下各板的荷载效应情况，同时也考虑车道荷载折减的影响，对于边板来说，得出的结果不是其最不利的工况。运行Midas Civil 结构模型，得到各主梁在车道荷载作用下的挠度，并计算相应的横向分布系数。考虑本桥的梁板数较多，本文仅对1 号边板（管架侧），9 号、10 号、11 号中板，19 号边板作为主要研究对象。在左边载作用下，为1 号边板、9号中板的最不利布载位置，主梁的挠度见表2。在中载作用下，得到10 号中梁的最大挠度，主梁的挠度见表3。在右边载作用下，为11 号中板、19 号边板的最不利加载位置，主梁的挠度见表4。

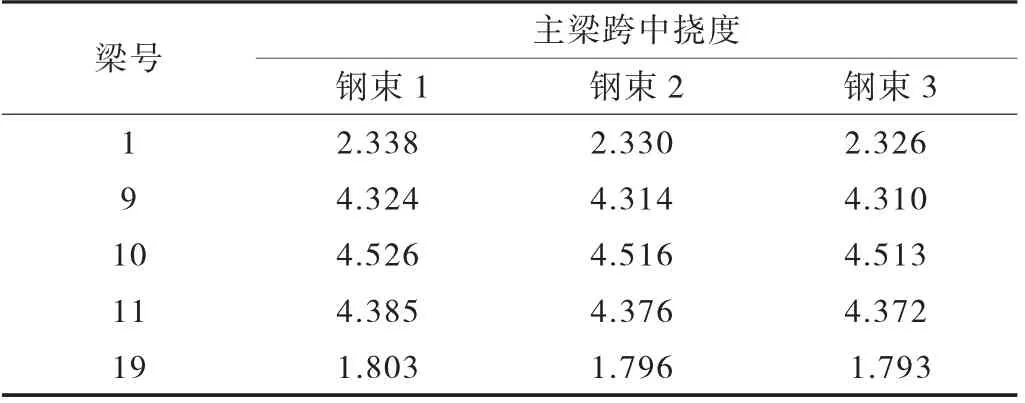
表2 左边载作用下的主梁跨中挠度

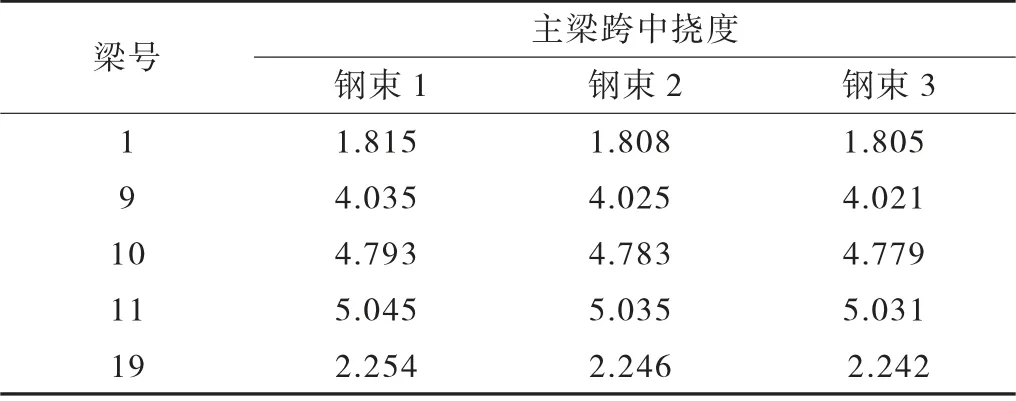
表3 中载作用下的主梁跨中挠度

表4 右边载作用下的主梁跨中挠度

通过对各主梁的最不利位置进行加载，得到它们的挠度值。然后依据挠度与横向分布系数的比值关系，求出不同钢束数量情况下，主梁的横向分布系数值（考虑车道折减系数），见表5。

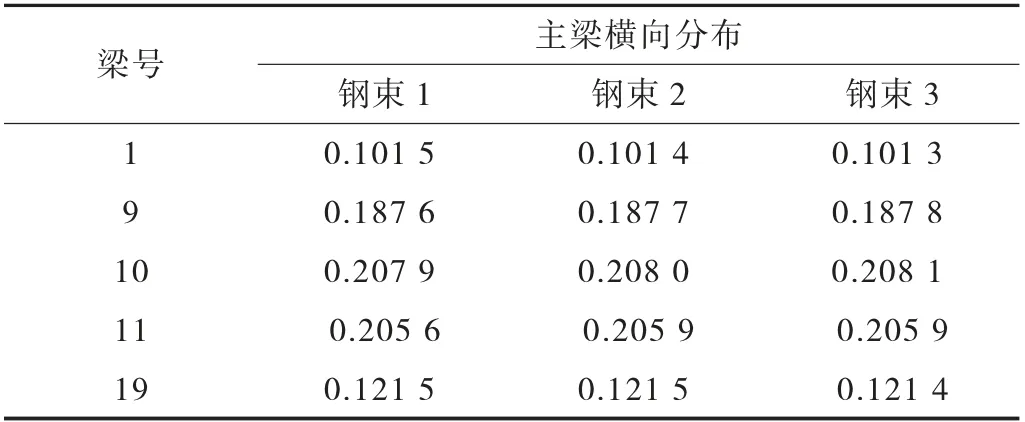
表5 梁格法计算横向分布系数

由表5 计算出的横向分布结果可以推断，梁格法模型中钢束数量的变化对空心板梁的横向分布有影响，但是很小，在实际设计过程中可以忽略。同时对较宽的桥梁结构，边板有随钢束增加，其横向分布减小的趋势；而中板随钢束增加，其横向分布增加。主要原因是钢束增加，其自身刚度加强，能承担更多的车道荷载。与边板相比，对作用其上的中板挠度值减少幅度小于边板。也就是说，钢束的增加对车道荷载作用下的中板的横向分布效应影响更为明显。

由表6、图4 可知。与Midas Civil 梁格法计算的结果相比，桥博计算的结果表现出各板的横向分布更为均匀。这可能主要是因为Midas Civil 中模拟的横向连系梁的刚度取值和桥博不同，或者本模型的横向连系梁的截面特性还有进一步优化的空间。如果考虑桥梁上部结构的二期铺装，将使计算的结果更偏向于桥博的取值。

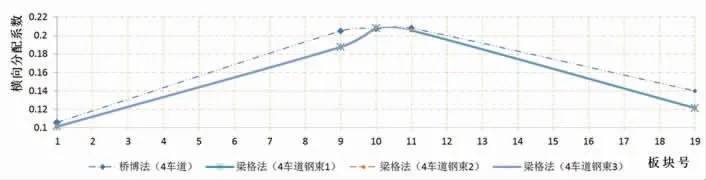
图4 横向分布系数分布图

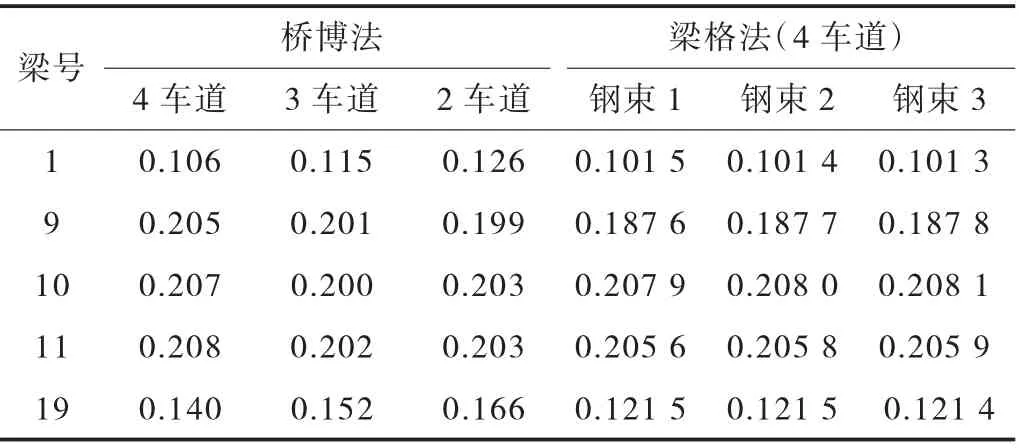
表6 桥博法与梁格法计算横向分布系数结果比较

5 结语

对比不同钢束下空心板横向分布的数值可以看出，适当钢束数量的改变对板梁自身略有影响，但是很小，实际设计过程中可以忽略。从桥博法计算和梁格法计算的结果对比可以得到，桥博中计算空心板的横向分布的均匀性更好，边板大于Midas Civil 计算的数值，中板小于Midas Civil 中计算的数值，实际设计中，采用桥博法计算的中板横向分布是偏于不利的，对中板横向分布的取值可以适当增加。