基于因子图结合卡方检测的多AUV协同定位方法
2021-10-27涂豫李国胜覃羡烘
涂豫,李国胜,覃羡烘
(1.河南工业职业技术学院,南阳473000;2.华中科技大学计算机科学与技术学院,武汉430074;3.郑州大学信息工程学院,郑州450001)
引 言
多自主水下航行器(Autonomous underwater vehicle,AUV)集群在水下军事勘探、深海海洋勘察、生物监测等领域得到了广泛的应用[1]。获取准确的位置信息是确保多AUV集群成功、高效执行任务的重要前提[2-3]。在恶劣的水下环境下,AUV的高精度导航已成为一个紧迫而艰巨的挑战[4-5]。“多AUV协同定位”(Cooperative localization,CL)是一种新的水下定位技术,主-从式多AUV协同定位系统可利用水声设备和低精度导航设备实现高精度水下定位,具有可期的研究前景[6]。
传统Kalman滤波是航行器导航定位中常用的技术手段[7]。但在协同定位系统中,当水声测距信息数量变化时,滤波算法的量测方程维数需要随时变化不利于计算。因子图(Factor graph,FG)将全局函数划分为局部函数,捕获数据的高阶统计信息,而不是常用的二阶统计信息[8-9],因子图相对于曼滤波方法最大的优势在于“即插即用”,更适用于实际的CL系统。文献[10]研究了一种基于FG关联状态与量测模型的定位方法,利用地磁匹配信息抑制算法误差,并进行了跑车试验;文献[11]结合FG提出了一种采用概率图模型的估计USV位置算法,可有效获得USV位置信息。上述方法都假设观测噪声为Gauss噪声,但在水下经常会出现一些特殊情况,复杂的水下环境很可能导致水声测距信息随时出现噪声异常值,这将严重影响AUV位置估计性能。因此,融合异常值信息的CL算法是水下机器人面临的主要挑战[12]。
卡方(χ2)检测方法可以用来反映观测信息与估计信息之间的偏离程度,常用于检测突变异常数据[13]。为了保障CL稳定性,本文提出一种将FG结合χ2检测的CL算法来计算测距噪声存在异常值时系统的位置信息。通过仿真实验验证,所提CL算法可有效抑制噪声异常值对AUV位置信息估计的影响,适用于水下多AUV协同定位问题。
1 多AUV协同定位系统模型
在实际的水下定位中,AUV的深度信息不会影响水平位置误差。因此,可将三维运动学模型投影在二维水平面,简化分析CL问题[14],如图1所示。
从-AUV的位置状态为(xk,yk),表示在tk时刻的位置坐标。

式中:xk和yk分别为tk时刻从-AUV的东向和北向位 置,Δt为采样间隔,v̂k为从-AUV在tk时刻的前向速度,θ̂k为航向角分别为tk时刻从-AUV的东向和北向噪声。所对应的离散状态方程为

式 中:Xk=[xk,yk]为 位 置 向 量;uk=[v̂k,θ̂k]为 传 感 器 输 入;状 态 函 数ωk时刻系统过程噪声。
相对距离关系为

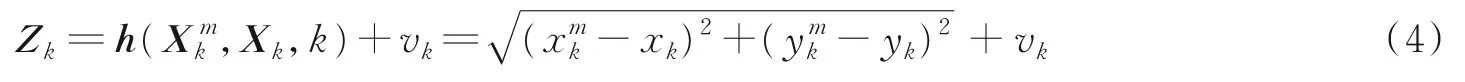
2 因子图与卡方检测
2.1 因子图与和积算法
FG包括变量和函数两种节点。函数节点代表的是局部函数,而与其相连的那些变量是其自身相关 的 自变量[11,15]。例如,g(X1,X2,X3)是包含4个 变 量 的全局函数,g1、g2、g3这3个是组成它的 局 部函数。
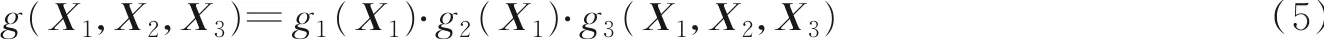
此全局函数的FG模型如图2所示。基于FG的问题通过“置信度信息”(Belief information,BI)在FG中传递。BI(gi,Xj)为gi到Xj的 置信 度 信 息,BI(Xj,gi)为Xj到gi的 置 信 度信 息,i=1,2,3,j=1,2,3。
BI表示变量的概率密度分布(PDF)。整个过程通过和积算法实现。如图2所示,以X1为例说明节点间BI需满足以下规则:
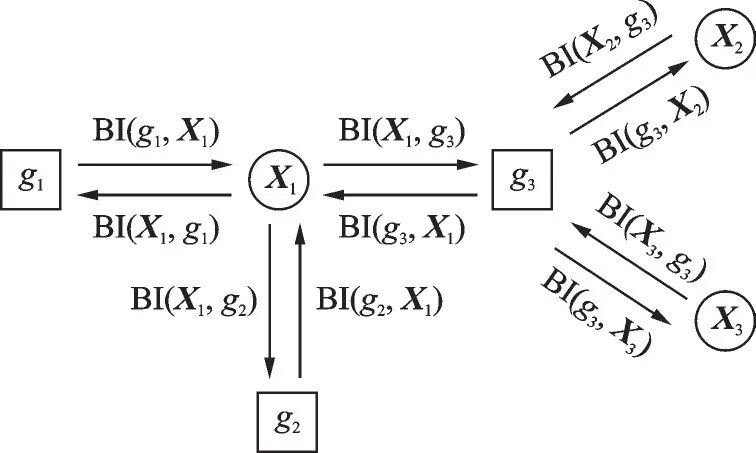
图2 FG模型示意图Fig.2 Schematic diagram of FG model
(1)从X1传递至g3的BI是所有来自其他相邻函数节点到X1的BI的乘积。
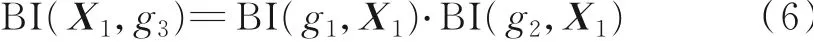
(2)g3传递至X1的BI是所有相邻变量节点传递至g3的BI与包含这些变量的函数的BI乘积,然后再对所有除此变量外的相关变量做积分所得。
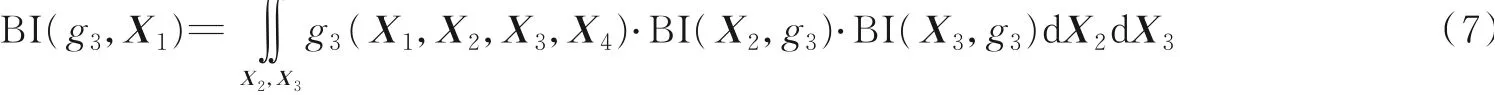
(3)由以上两个规则可推导出,X1的BI等于所有相邻的函数节点到X1的BI的乘积。
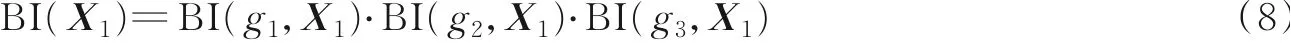
2.2 残差χ2检测
量测残差可以表示为

式中:Zk为实际测距为系统测距预测值。
水声测距残差δZk的方差为

式中:p为采样周期常数,通常取值为5~10。
当水声声测距噪声存在异常值时,δZk便不再服从Gauss分布,δZk的统计特性即可判断系统是否故障。构造统计量

式中:λk~χ2(m),m为量测方程维数。故障判定准则为:若判定CL系统测距噪声异常判定CL系统正常为检测门限,α为虚警率。利用残差χ2检验法可以完成对突变噪声的检测。
3 基于因子图与χ2检测的协同定位
将CL问题简化为多个一维问题,x轴坐标和y轴坐标分别用FG中的两组节点表示这两个一维问题。如图3所示,Ai、Bi、Ci、Di、Ei为函数节点;x̂*k、ŷ*k、xk、yk、Δxi、Δyi、di为变量节点;i表示为第i条主-AUV。
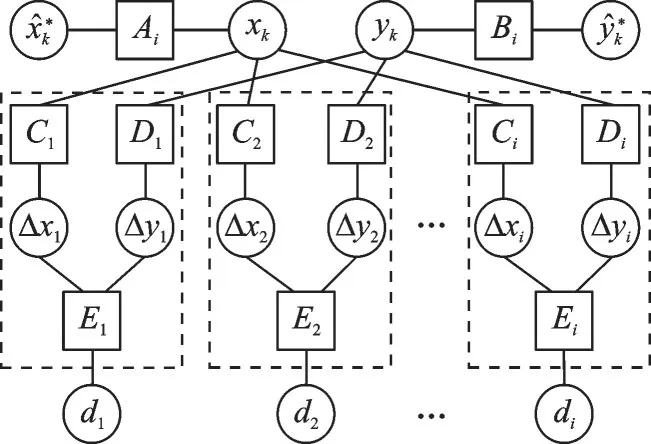
图3 基于FG的CL算法示意图Fig.3 Schematic diagram of CL algorithm based on FG
函数节点Ci,Di的约束关系为

函数节点Ei的约束关系为


在AUV开始时,通常可以确定初始位置。CL算法具体步骤为:
(1)初始化
在CL初始时刻,从-AUV的初始位置确定为
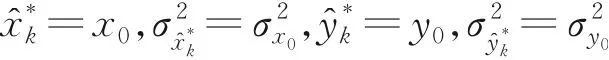
在非初始时刻,位置状态计算为

从-AUV位置状态的期望和方差分别为
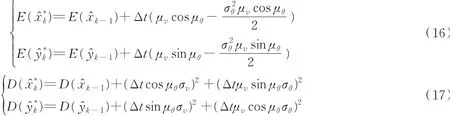
从-AUV航位推算位置的期望和方差由式(16)和式(17)更新。
第i次迭代后,计算得到xk和yk的概率密度分布为

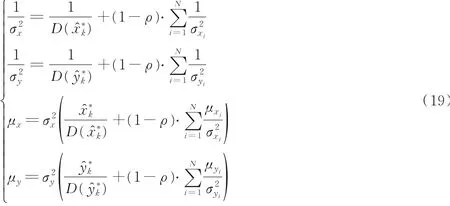
式中:N为从-AUV同时观测到的量测信息的数量,μxi和μyi为第i个主-AUV估计的位置坐标的数学期望观测信息为第i个主-AUV估计的位置坐标的方差;ρ为χ2检测的异常值标志位,若则ρ=1,若则ρ=0。
(3)更新Ci和Di
从函数节点Ci、Di传递到变量节点Δxi和Δyi的PDF可以分别表示为
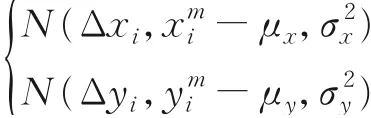
从函数节点Ci、Di传递到变量节点xk和yk的PDF可以分别表示为

(4)更新Ei
根据勾股定理,变量节点Δxi和Δyi之间的约束可以描述为

从函数节点Ei传递到变量节点Δxi和Δyi的PDF可分别表示为

式中:Δxi和Δyi分别表示在之前的迭代中主-AUV与从-AUV的x轴和y轴坐标差值为 相 应 的方差。
4 仿真实验分析
在协同定位系统中,主-AUV装备高精度惯性导航系统(INS),从-AUV装备低精度的罗盘用来提供航向。主-AUV与从-AUV均装备DVL及声呐,用来实现AUV中间的相互距离测量与通信,图4为传感器布局及通信示意图。

图4 水下声学通信示意图Fig.4 Schematic diagram of underwater acoustic communication
本文通过数值仿真实验对因子图结合χ2检测算法处理水声测距噪声异常值影响的有效性进行验证。由于AUV的深度信息通常由深度传感器直接测得,且各AUV的深度不会影响水平位置的计算,因此该仿真实验中不考虑AUV深度信息。仿真实验中设置声信号在水中的传播速度为1 531 m/s。图5为主-从AUV在平面直角坐标系中的运动轨迹,AUV坐标单位为m。
其中两艘为主-AUV,设置主-AUV起始坐标分别为(2 000,1 000)和(4 000,1 000),一艘从-AUV的起始坐标为(3 000,2 000);初始航向角均为30°,航向角速率为0.005(°)/s;主从-AUV航行速度均为5 m/s;采样频率为1 Hz;总实验时间为3 600 s。仿真实验模拟传感器设置参数如下:主-AUV航向角噪声均值为0,方差为(0.5°)2,从-AUV航向角噪声的均值为0,方差为(0.8°)2;航向漂移为3(°)/h;量测噪声的均值为0,方差为(5 m)2,且两个水声测距值是独立的、无关的。仿真参数设置符合实际水下协同定位系统实验。航位推算、基于EKF算法和FG算法的CL误差曲线如图6所示。
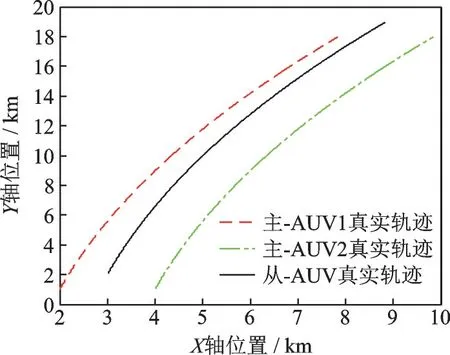
图5 主-AUV和从-AUV的基准航行轨迹Fig.5 Reference trajectories of master-AUV and slave-AUV
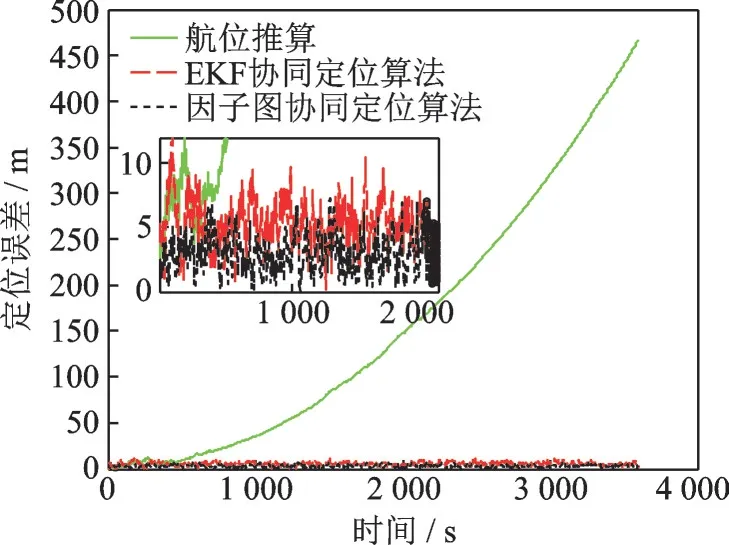
图6 从-AUV定位误差对比图Fig.6 Slave-AUV positioning error comparison diagram
为了模拟实际水声测距噪声出现异常值,在仿真实验中加入如图7所示的突变测距噪声。
由水下特殊环境导致的测距噪声异常值严重影响AUV定位精度。此时,利用残差χ2检验法构造χ2统计量,检测测距残差的变化,将噪声异常值当做系统故障处理,舍弃异常时刻的测距信息,可以有效减小CL误差。接下来将基于图7的测距误差对CL系统仿真实验。
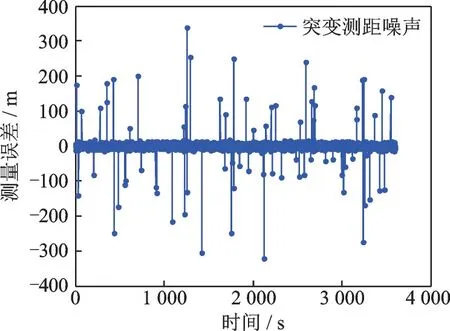
图7 多AUV系统测距噪声异常值Fig.7 Multi-AUV system noise outliers
设置χ2检测的误警率为0.01,查χ2分布临界值表得对应的门限值为6.635;χ2检测结果如图8所示。
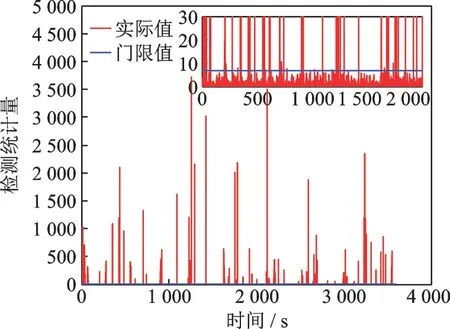
图8 卡方检测的测距噪声异常值检验统计量Fig.8 Test statistics of ranging noise outliers detected by chi-square
分别应用FG和FG结合卡方检测算法估计从-AUV轨迹曲线和定位误差曲线如图9、10所示。
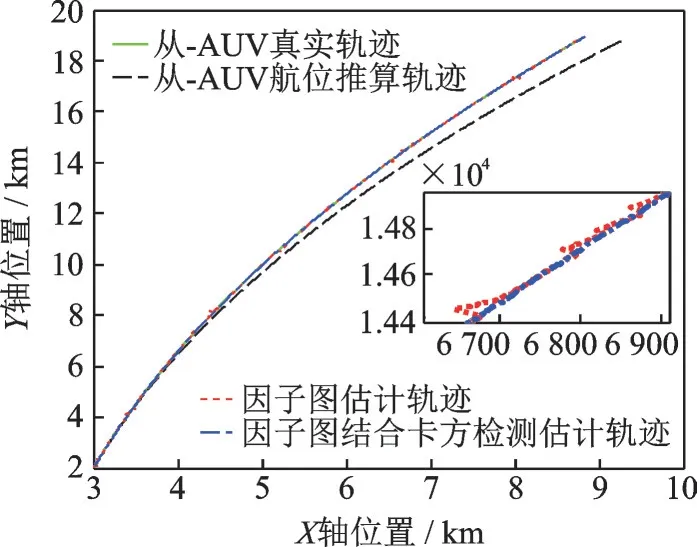
图9 测距噪声异常值情况下从-AUV轨迹曲线对比图Fig.9 Comparison of slave-AUV trajectory curve in the case of abnormal value of ranging noise
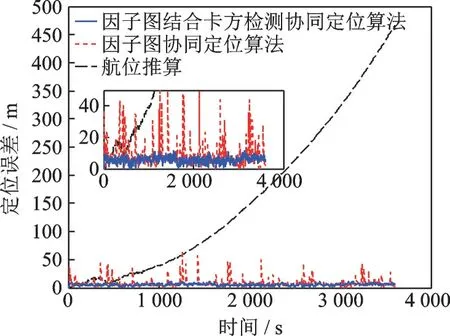
图10 测距噪声异常值情况下从-AUV定位误差对比图Fig.10 Comparison of slave-AUV positioning error in case of abnormal value of ranging noise
各算法定位误差的均值和均方根误差如图11所示。在如图7所示测距噪声条件下,FG算法的平均误差为7.82 m,均方根误差为10.36 m;FG结合卡方检测算法的平均误差为5.67 m,均方根误差为5.99 m。
总结上述实验,基于EKF的CL算法精度低于基于FG的CL算法精度,因子图更适用于协同定位系统的实际应用。在测距噪声异常的情况下,本文所提出的基于FG结合χ2检测的协同导航方法具有更高的定位精度,适用于解决测距噪声出现异常值情况下的CL问题。
5 结束语
本文提出的因子图与卡方检测结合定位方案,在水声测距系统出现测距噪声异常值情况下,可提高协同定位可靠性。具体优势如下:
(1)所提算法计算过程简便,易于实现,在水声测距噪声为高斯噪声前提下,具有很好的定位稳定性。
(2)在水下声学测距噪声出现异常值时,所提算法可有效抑制量测噪声的干扰并具有足够的稳定性,可保证水下协同定位系统安全健康运行。
