纯电动客车电驱动系统综合性能灰色关联评价

赵国朋，王 波，王晓彬，钱亚男，黄玉鹏

(中通客车股份有限公司，山东 聊城 252000)

纯电动客车动力系统的核心是电驱动系统，选择一个合适的电驱动系统是提高整车动力性、经济性的关键[1-2]。电驱动系统性能的优劣取决于很多的因素，目前选择电驱动系统主要依据工程师的经验，受工程师的主观性影响比较大。灰色关联分析法是通过对已有的数据进行合理的加工，根据层次间的关联度来确定评价指标，具有计算量小、不受主观因素影响的优点。本文使用灰色关联分析法对电驱动系统综合性能进行评价，根据电驱动系统的关联度来选择最优方案[3-4]。

1 灰色关联分析法

灰色关联分析法根据各因素变化的相似程度，来判断各因素之间关联程度。如果这两个因素间的关联度较大，则认为这两个因素的变化趋势是一致的，否则认为这两个因素的变化趋势不一致[5]。灰色关联分析法的操作步骤如下：将需要评价的指标进行无量纲化处理，构建决策矩阵，计算关联系数，计算关联度，最后根据关联度的大小进行排序，关联度最大的为最优方案。

1.1 建立决策矩阵

电驱动系统的多种指标间都有不同的量纲，需要根据指标的分类进行无量纲处理[6]，方法如下：

首先根据表3中的n个指标分别对m种电驱动系统进行实验，建立实验数据矩阵：

(1)

式中：xij为第i种电驱动系统中第j个指标的实验数据。实验数据分为效益型指标和成本型指标。效益型指标包括高效率区间、控制精度等；成本型指标包括电机质量、电机价格等。

然后对式(1)中的实验数据xij进行无量纲处理，若是效益型指标，处理如式(2)所示，若是成本型指标，处理如式(3)所示。效益型指标越大，处理后的数据越接近于1；反之，越接近于0。成本型指标越小，处理后的数据越接近于1；反之，越接近于0。

(2)

(3)

再用无量纲处理后的数据rij建立决策矩阵：

(4)

1.2 建立关联系数矩阵

根据决策矩阵(4)选取每项指标rij的期望值构建电驱动系统期望指标行矩阵R0：

R0=[r01,r02,…,r0j,…,r0n]1×n

(5)

式中：r0j(j=1,2,…,n)代表对电驱动系统中第j个属性指标的期望值，一般每一项都取rij的最优值，即r0j=1，从而R0=[1,1,…,1]1×n。

计算决策矩阵R与期望指标矩阵R0的绝对差矩阵Δij和关联系数ξij：

Δij=|rij-r0j|

(6)

(7)

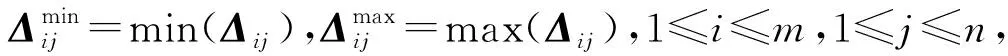
(8)

式中：关联系数ξij是不超过1的正数，它反映了第i种电驱动系统中第j个指标值与第j个指标期望值的关联程度。

1.3 建立层次结构模型

根据电驱动系统性能评价指标确定其层次结构模型，自上而下分为A、B、C、D 4个层次，其中B、C、D层次根据不同指标进行分类，如图1所示。图1中的各类指标见表3。

图1 电驱动系统的层次结构模型

由于各个指标在评价体系中的重要性不同，所以有必要引入对各个指标的相对重要性进行度量(即权重)。采用判断矩阵可以对一系列指标的相对重要性进行量化分析[8]。针对图1所示的层次结构模型，Santy等人提出应用表1中的1～9量化值构建判断矩阵[9]A，来表示本层某两个指标和其上层中与之有关的指标之间相对重要性的比较。表1中的数值表示本层中两指标相对上层中某一指标的不同重要性的比较。例如，B层中指标对于A层指标的重要性比较为：B1指标比B2指标稍微重要，则a12=3。

(9)

式中：apq(1≤p≤k，1≤q≤k)根据表1取值，k为图1中每层的指标个数。

表1 判断矩阵中apq的取值表

将式(9)判断矩阵A的最大特征值λmax的特征向量W经归一化后可得到某层指标对于上一层指标的权重。

1.4 一致性检验

1.3节最后得到的是每层中相关指标的排序权值，需要通过式(10)、(11)进行式(9)的一致性间接检验。只有判断矩阵通过该一致性间接检验后，才可认为所建立的判断矩阵是有效的。

1) 计算一致性指标CI。

CI=(λmax-k)/(k-1)

(10)

式中：k为式(9)中每层的指标个数，即式(9)中的矩阵阶数。

2) 采用式(11)计算一致性比例，式中RI取值见表2。

CR=CI/RI (11)

表中k的意义与式(10)相同。当CR<0.1时认为判断矩阵的一致性是可以接受的，否则认为判断矩阵的一致性是不可以接受的。

1.5 关联度系数的确定

确定了各个指标的权重和关联系数之后，根据式(12)可以计算出各方案的关联度：

(12)

式中：wj(j=1,2,…,n)是第j个属性指标的权重，n为待评价的属性指标个数；ξij(i=1,2,…,m；j=1,2,…,n)为关联系数；m为待评价的电驱动系统种数。

根据ri的取值，可以确定各个方案的优劣，若关联度ri最大，说明第i个被评对象优于其他被评对象，据此可以排出各被评对象的优劣次序[10]。

2 实例验证

对4个厂家的电驱动系统进行台架试验和CCBC工况试验，取得的实验数据见表3。使用本文提出的灰色关联分析法对电驱动系统进行综合评价。

表3 不同厂家电驱动系统实验数据

1) 根据式(1)建立实验数据矩阵：

(13)

2) 建立决策矩阵。根据式(2)、(3)分别对一些成本类属性指标和效益类属性指标进行无量纲变化，根据式(4)建立标准化决策矩阵。

高效率区间(D1)为效益性，根据式(1)计算得到r11=(90.65-83.43)/(92.18-83.43) =0.825，同理，r21=1，r31=0.825，r41=0；建立决策矩阵R如下：

(14)

3) 根据式(5)建立最优属性指标矩阵：

R0=[1,1,…,1]1×23

4) 根据式(6)计算绝对差矩阵，Δ11=|0.825-1|=0.175，Δ21=|1-1|=0。同理，建立绝对差矩阵Δ如下：

(15)

5) 取分辨系数ρ=0.5，根据式(7)、(8)确定关联系数矩阵，ξ11=(0+0.5×1)/(0.175+0.5)=0.741，同理，根据计算ξij建立关联系数矩阵D如下：

(16)

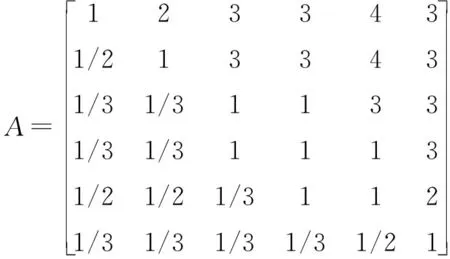
6) 建立判断矩阵。根据图1所示的层次结构，可以建立A-B、B1-C、B2-C、B3-C、C1-D、C2-D共6个层次间的判断矩阵。举例B3-C层判断矩阵建立过程：根据图1，B3具体对应C4。根据表3，对B3而言C4指标中的最大爬坡度指标比0～50 km/h加速性能指标的重要性介于同等重要和稍微重要之间，根据表1取值为2；相反地，0～50 km/h加速性能指标相比最大爬坡度指标的重要性取值为1/2。最高车速指标比0～50 km/h加速性能指标稍微重要，取值为3；相反地，0～50 km/h加速性能指标相比最高车速指标的重要性取值1/3。12%坡度时性能指标比0～50 km/h加速性能指标稍微重要，取值为3；相反地，0～50 km/h加速性能指标相对12%坡度时性能指标取值1/3。同理可以建立其他指标相对于0～50 km/h加速性能指标的重要性。最高车速指标相对于最大爬坡度指标稍微重要，取值3；相反地，最大爬坡度指标相比最高车速指标对的重要性取值1/3。同理对其他指标相对重要性进行取值，建立B3-C4层判断矩阵如下：

(17)

同理，共建立6个各层次间的判断矩阵。

7) 使用MATLAB按照式(10)、(11)计算得到各层次的一致性指标和一致性比例见表4，总排序一致性检验CR=0.061 738，CR<0.1，整体满意。

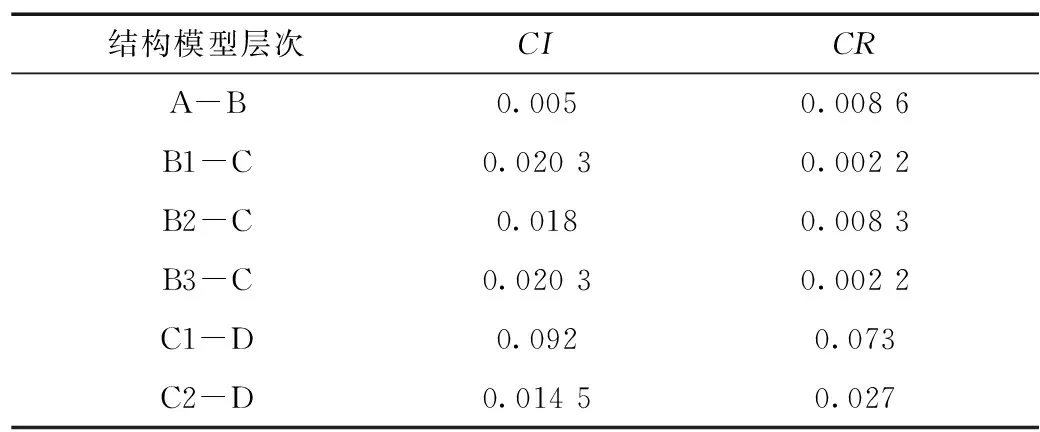
表4 驱动电机的递阶层次参数计算结果

8) 根据表4进行归一化处理后得到各项类指标的权重ωj如下：高效率区间，ω1=0.025 1；系统最高效率，ω2=0.008 3；…；4%坡度时速度，ω23=0.009 6。

9) 将上述各权重值代入式(12)，最终计算出各厂家电驱动系统的属性指标关联度：r1=0.81，r2=0.63，r3=0.58，r4=0.54。所以厂家1的电驱动系统综合性能是最好的。

3 结束语

本文使用灰色关联分析法将电驱动系统中的关键指标都列入综合评价体系中，求出评价体系中各指标的权重和关联度，最后根据关联度数值的大小选出综合性能最优的电驱动系统。