基于IDA的套箍加固拱上立柱抗震性能评估
2021-10-26钱永久
唐 堂, 钱永久, 王 磊
(1. 四川华腾公路试验检测有限责任公司, 四川 成都 611730;2. 西南交通大学土木学院, 四川 成都 610031)
0 引言
我国西南地区多为高地震烈度的山区,地形、地貌和地质条件复杂,山区桥梁结构通常采用大跨度钢筋混凝土拱桥。由于拱桥结构刚度大,主拱桥截面轴压比大,延性差,大跨度拱桥被认为是抗震性能相对较差的桥型。2008年“5·12”地震中,四川地震灾区多座大跨径混凝土拱桥发生了不同程度的震害,其中金花大桥和白水河的大桥的拱上立柱震害十分典型。近年来,国内外不少学者采用增量动力分析(IDA)对不桥梁进行抗震性能评估分析研究,取得了一系列的成果[1-5]。研究重点主要针对桥墩和框架结构,但对拱上立柱抗震性能研究还很少。本文将以基于增量动力分析对德阳金花大桥的拱上立柱进行分析,为既有钢筋混凝土拱上立柱和套箍加固立柱的抗震性能评估提供理论依据。
1 工程实例
绵竹金花石亭江大桥位于绵竹市红白镇至金花镇公路。桥位跨越石亭江,拱轴线与石亭江流向交角为65°。桥跨组合:4×9.5 m简支梁+1×150 m双肋拱+2×9.5 m简支梁,桥梁全长228 m;桥梁全宽10.0 m(9.0 m净宽+2×0.5 m防撞护栏)。下部结构为重力式墩台、钻孔灌注桩基础。桥面双向1.5%横坡,桥面纵坡为2.66%。桥梁设计荷载:汽车为20级,挂车为100级。地震基本烈度:Ⅶ度,地震动峰值加速度为0.15g。大桥建成于1997年。主拱采用C40钢筋混凝土等截面悬链线箱形双肋拱,净跨径150 m,拱轴系数m=2.111,矢跨比f/L=1/6,肋间中距6.4 m。单肋截面为双箱双室,箱宽3.0 m,箱高2.3 m;顶板厚0.28 m,底板厚0.25 m,顶底板在拱脚18 m区段,按线形分别逐渐加厚到0.48 m和0.45 m,腹板为3×0.25 m。拱上立柱和引孔墩柱为C30钢筋混凝土结构。支座采用(GJZ300×700×42)的板式橡胶支座或聚四氟乙烯滑板支座。伸缩缝采用TST弹塑体与碎石填充伸缩缝(1)绵竹金花大桥检测报告,成都:四川华腾公路试验检测有限责任公司,2008:15.。
由于金花大桥桥址在龙门山断裂带附近,本次汶川地震波的峰值加速度很大。大桥各个构件均发生了不同程度震害,其中拱上立柱柱底存在环向贯通裂缝(图2~3)。针对立柱震害,加固设计单位对立柱底部采用钢筋混凝土套箍进行加固(2)绵竹金花石亭江大桥加固施工图设计文件.成都:四川省交通厅公路规划勘察设计研究院,2008,4.。在纵桥向,立柱两侧各增加10 cm厚C40混凝土,与立柱底座平齐;在横桥向,加固顶部增加10 cm厚C40混凝土;在竖直方向上,从立柱底座顶面起向上延伸55 cm。加固前后的立柱构造图见图4~5所示。

图1 金花大桥立面图Fig.1 Vertical section of Jinhua Bridge

图2 SC2拱上立柱柱底环形裂缝Fig.2 Annular crack at the bottom of spandrel column SC2

图3 SC9拱上立柱柱底环形裂缝 Fig.3 Annular crack at the bottom of spandrel column SC9

图4 既有立柱构造图(单位:cm)Fig.4 Section of existing spandrel column (Unit:cm)
2 地震效应分析
2.1 计算模型
采用SAP2000软件建立金花大桥的三维有限元模型,全桥计算模型如图6所示。在计算模型中,主拱肋、纵梁、垫梁采用空间梁单元模拟,桥面板采用板壳单元模拟。拱上立柱的弹塑性模型在其柱底和柱顶设置塑形铰,铰的恢复力特性由弯矩-轴力相互作用的屈服面定义。全桥模型包括 200个梁单元,150个板单元。根据结构实际支撑情况和场地条件,拱肋边界条件取与地基固结,拱上立柱与主拱肋采用刚性连接,拱上立柱与纵梁连接采用板式橡胶支座或聚四氟乙烯滑板支座连接。在计算模型中,板式橡胶支座采用Link型单元中Plastic(Wen)用以模拟,竖向刚度取值κ=660 mN·m-1如图7所示。聚四氟乙烯橡胶支座的恢复力模型采用双线性模型,SDX=6.6×105kN·m-1,SDY=SDZ=1 437 kN·m-1,支座旋转刚度取值为0,如图7所示。计算模型中考虑地震时桥面板与桥台之间、引桥与主桥之间和在纵梁和垫梁之间的碰撞效应。在SAP2000中采用GAP单元模拟伸缩缝,刚度取值κ=5.76×107N·m-1,单元缝隙Open=0.044 m,如图8所示。
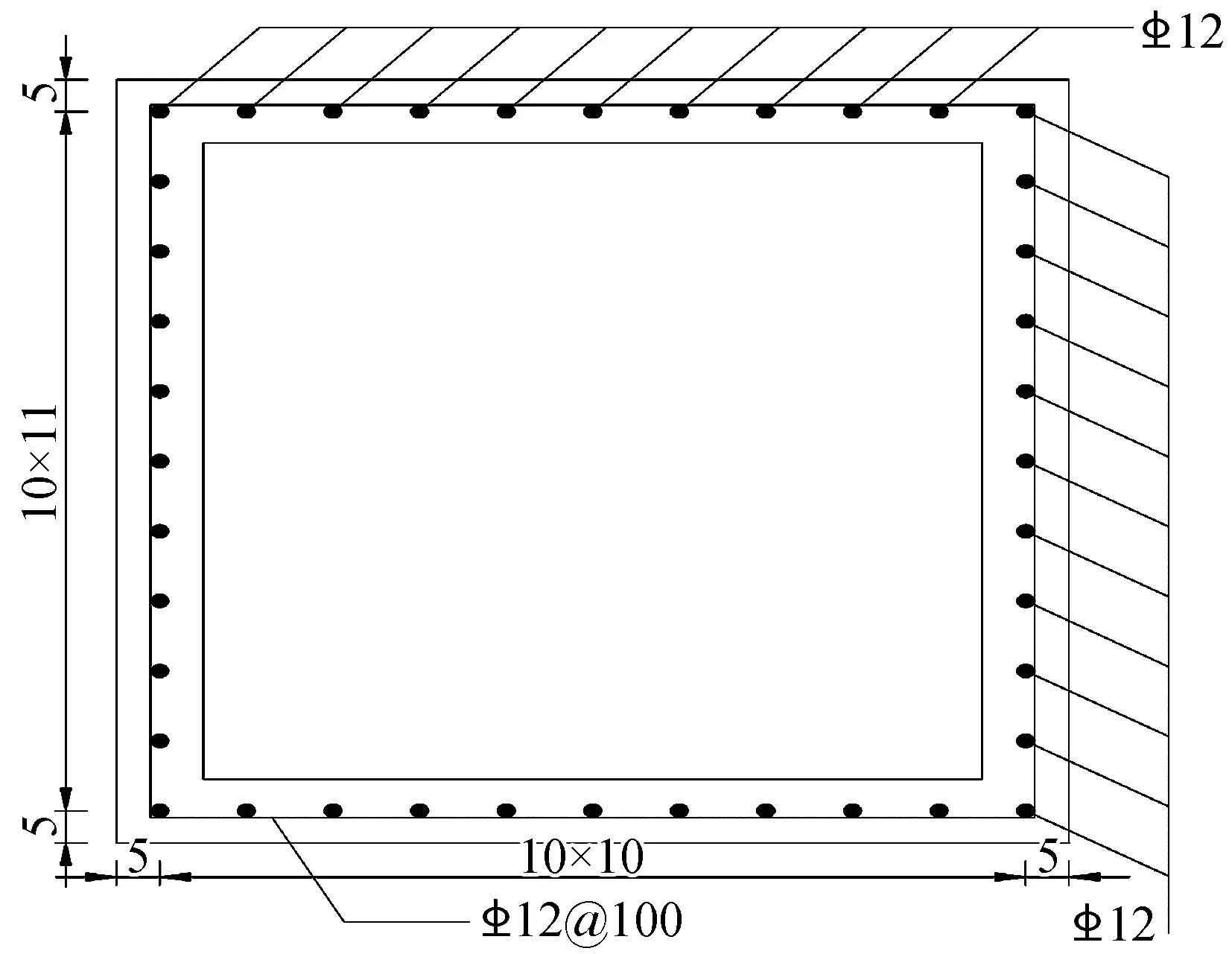
图5 套箍加固立柱构造图(单位:cm)Fig.5 Section of spandrel column strengthened by jackets (Unit:cm)

图6 金花大桥有限元模型Fig.6 The finite element calculation model of Jinhua Bridge
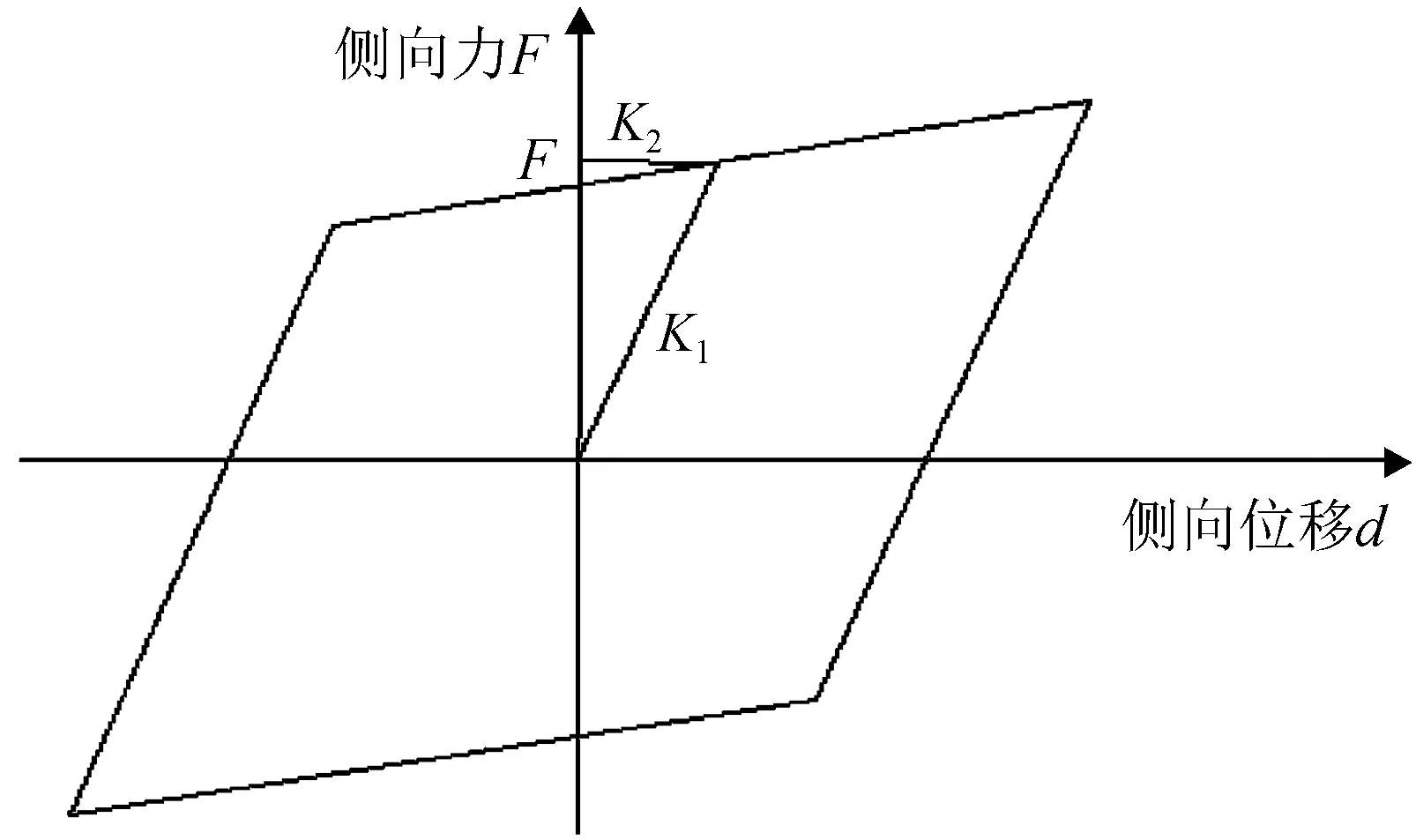
图7 滑板支座恢复力模型Fig.7 Resilience model of sliding bearing
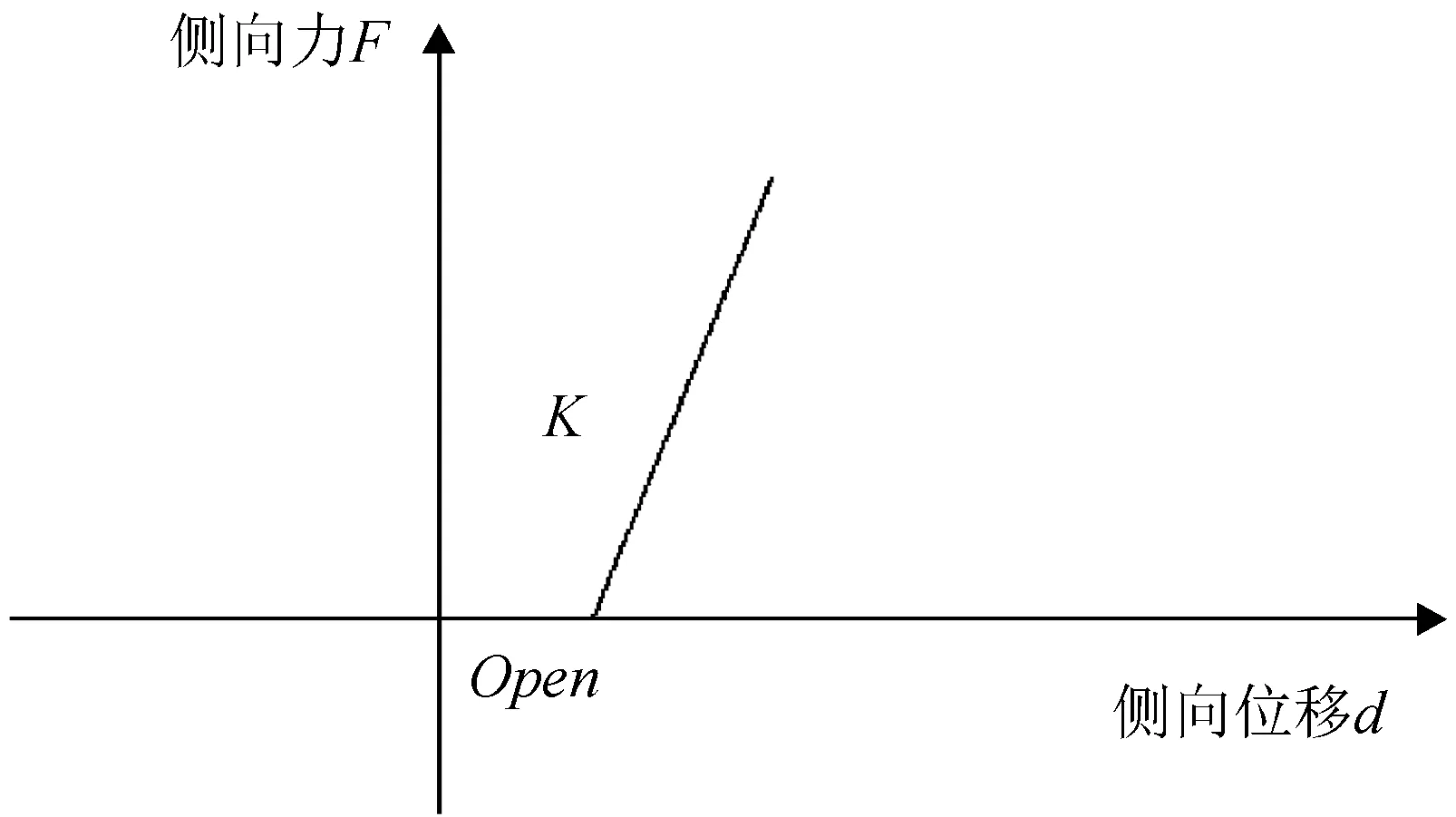
图8 伸缩缝采用GAP模型力-位移模型Fig.8 Force-displacement model adopted for expansion joint
2.2 地震动选取及调幅
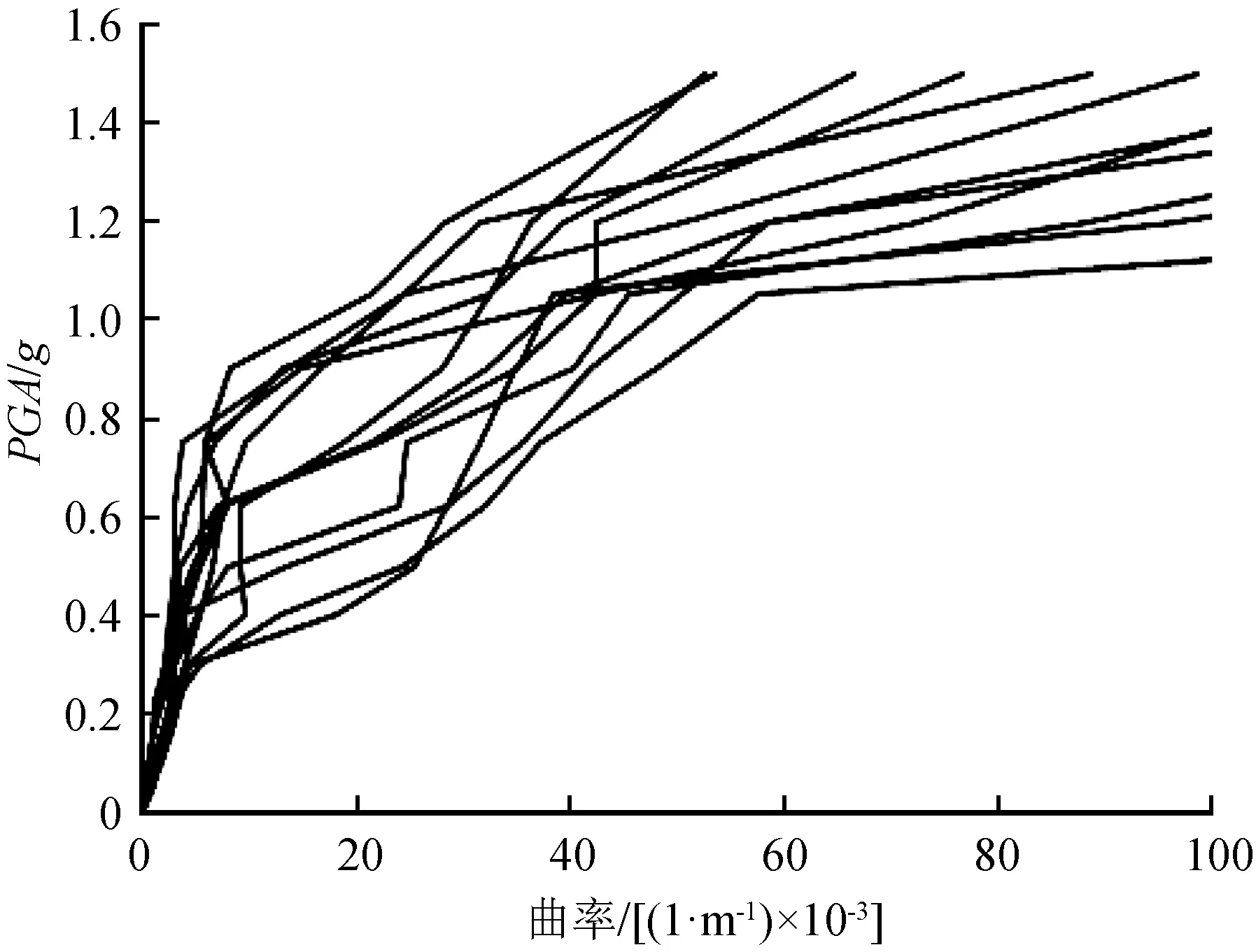
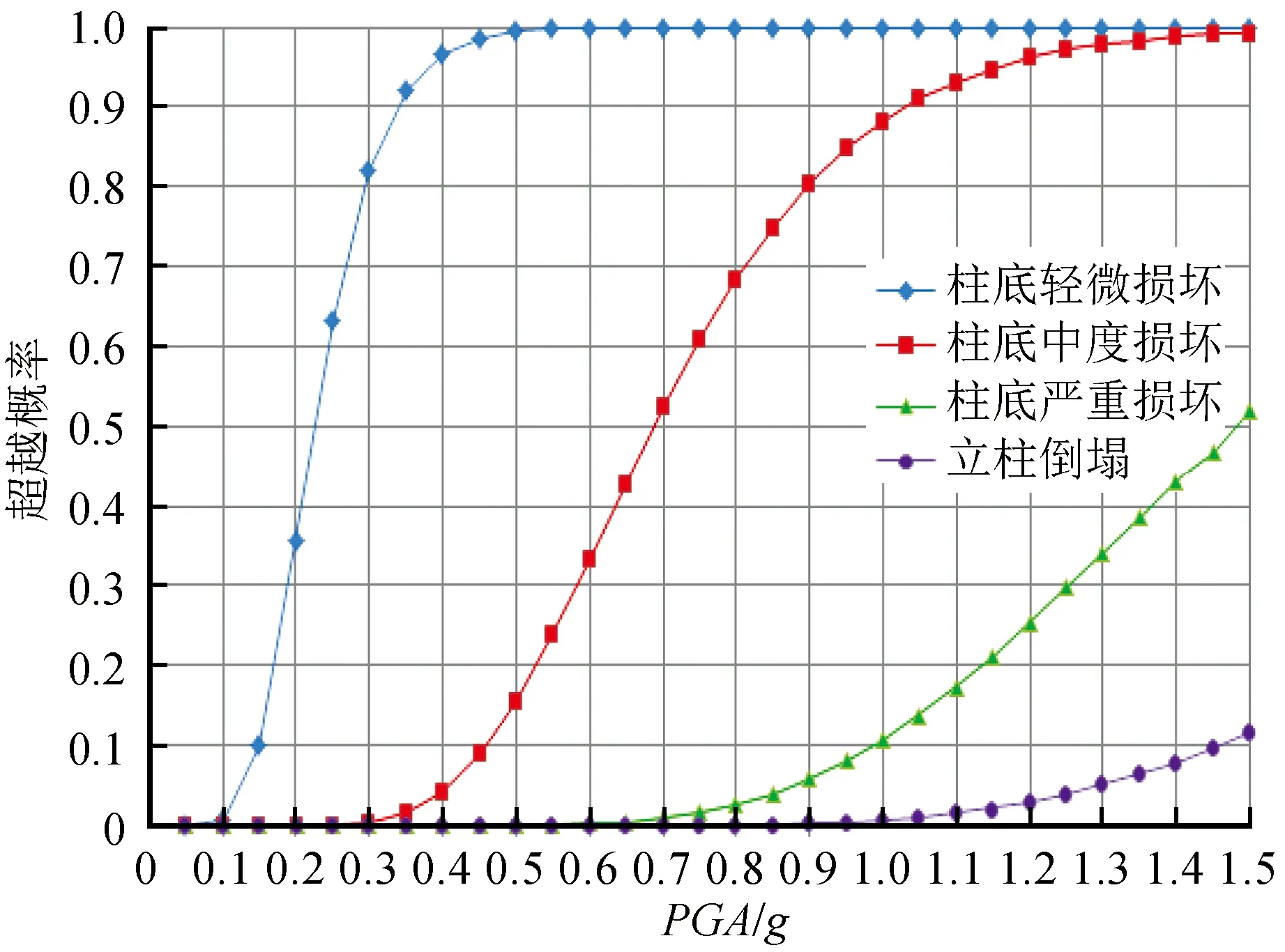
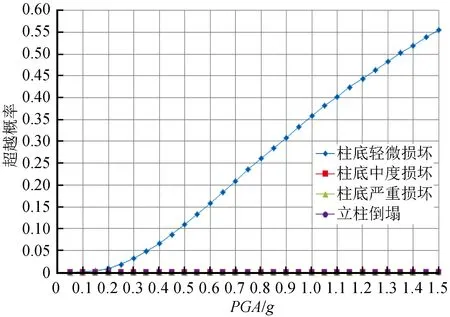
所选地震动记录来源于太平洋地震工程研究中心数据库(Peer Ground Motion Database)和汶川实测地震动,本次一共取了12条地震波,见表1、图9。地震动输入仅考虑纵桥向结构响应。本桥场地为Ⅱ类,覆盖层厚度介于3~50 m之间,参照《公路桥梁抗震设计细则》(JTG/T B02—01—2008)[6]第4.1.8条,地震动的平均波速设置为140 m/s 图9 加速度反应谱对比(ζ=0.05)Fig.9 Comparison of response spectra (ζ=0.05) 表1 计算采用地震动记录及地面峰值加速度调幅表 拱上立柱的损伤指标DM可通过截面的弯矩曲率关系来确定。根据上模型中立柱的截面特性及实际受力情分别求解柱底与柱顶截面弯矩曲率关系曲线如图10~图11。比较两图可知,SC1柱顶的延性明显优于SC1柱底,结合实际震害,在地震中首先失效的也是柱底位置。因此,本文在IDA分析时选取柱底曲率作为DM指标。 图10 SC1立柱顶部弯矩-曲率曲线Fig.10 Moment-curvature curve at the top of spandrel column SC1 图11 SC1立柱底部弯矩-曲率曲线Fig.11 Moment-curvature curve at the bottom of spandrel column SC1 3.2.1 非线性分析结果 以本文所选的12条地震动为基础,将PGA作为IM指标,按目标值对地震动进行幅值调整,使加速度峰值从0.05g逐渐增大至1.50g。利用得到的12组地震动分别对计算模型进行非线性时程分析结果如图12~13所示。 图12 SC1底部曲率IDA曲线Fig.12 IDA curve of curvature at the bottom of spandrel column SC1 图13 SC5底部曲率IDA曲线Fig.13 IDA curve of curvature at the bottom of spandrel column SC5 分析可知:(1)由于地震波特性的差异,不同的地震动对应位移、曲率曲线均有一定的数值差异,但这种离散差异在弹性阶段表现较小。在受力进入弹塑性阶段后,结构非线性特征和差异离线性得到明显体现。(2)在逐渐增大的地震动作用下,最长立柱(SC1)和最短立柱(SC5)的柱顶位移曲线差异显著,SC1柱顶位移并没有表现出明显的屈服平台,且离散性较大,SC5立柱屈服平台不明显,离散性相对较小,其主要原因在于立柱的相对刚度差异较大。SC1立柱本身较柔,位移反应较大,在较小的地震动峰值下就易弯矩屈服,当结构屈服后的刚度变小,地震动增加对柱顶位移反应的影响并不明显;SC5立柱相对较刚,位移反应较小,但其位移表现为非线性。此外,由于SC1立柱和SC5立柱位于拱肋的不同位置,在地震作用下,拱肋的变形亦会对立柱的变形产生明显影响。(3)对于单个地震动的IDA曲线而言,曲线能在PGA不断增大的前提下反映结构从弹性阶段到破坏的全过程。(4)结构在屈服之前,曲率大致随地震动强度增加呈线性变化;结构达到屈服后,塑性铰形成,曲线表现出明显的屈服平台,曲率斜率下降,表现出一定的延性能力,当地震动强度增加到一定值时,曲率急剧增加,直到结构倒塌。 3.2.2 概率分位曲线 对于IDA曲线进行分析时,为明确立柱的不同破坏状态,参照文献[7],依据立柱的曲率采用5级损伤状态界定立柱的不同破坏状态。本文用50%概率分位曲线表征地震响应的平均水平,用16%或84%概率分位曲线表征地震响应的离散程度。对最长立柱、最短底部曲率的IDA曲线进行统计分析,结果见图14~15所示。通过IDA概率分位曲线,既可以更直观地判断拱上立柱在不同强度地震下可能出现的损伤情况,又能清楚的确定在损伤范围内结构能抵抗的最大地震强度。 图14 SC1底部曲率的三水平概率分布曲线Fig.14 Probability distribution curves of curvature at the bottom of spandrel column SC1 图15 SC5立柱底部曲率的三水平概率分布曲线Fig.15 Probability distribution curves of curvature at the bottom of spandrel column SC5 从图14~15可知,当PGA在0.225g以内的SC1立柱和PGA小于0.75g时的SC5立柱,结构不开裂,处于正常完好状态,不经任何修复即可使用;当PGA位于0.225g~0.35g的SC1立柱和当PGA位于0.75g~0.85g时的SC5立柱,结构混凝土出现微小裂缝,但仍然基本处于弹性阶段,结构损伤程度较小,震后仅对裂缝进行修补即可正常使用;当PGA超过0.35g的SC1立柱和当PGA超过0.85g时的SC5立柱,立柱底部可能形成塑性铰,立柱通过塑性铰的转动消耗能量,钢筋开始屈服,混凝土表面明显开裂;当PGA超过0.8g时的SC1立柱和当PGA超过1.05g时的SC5立柱,立柱底部塑性铰区内混凝土出现剥落现象,结构已达到严重损坏的状态,在震后需要加固处治;当PGA继续增大至1.05g以上时的SC1立柱和当PGA继大于1.1g以上时的SC5立柱,立柱底部曲率超过极限曲率,立柱底部完全破坏,可能倒塌现象。综上所述,对于长立柱而言,相对较柔,其往往靠近拱脚位置,更容易发生破坏;对于短柱,其相对较刚且大多远离拱脚,其抗震性能明显较好。 地震动易损性是指结构在不同强度的地震动下,发生不同破坏程度的可能性或者说是结构达到某一特定状态的概率。基于IDA分析结果,本次研究采用理论方法进行,对分析结果进行整理和统计,得到地震易损性曲线,运用该曲线对结构破坏状态和抗震性能进行评估(图16~17)。 图16 SC1立柱回归分析结果图Fig.16 Regression analysis result of spandrel column SC1 图17 SC5立柱回归分析结果Fig.17 Regression analysis result of spandrel column SC5 对线性回归结果进行变换,最长立柱、最短立柱的曲率亦即地震需求D可分别表示如下: DA1=φA1=0.029 02×(PGA)1.587 7 (1) DA5=φA5=0.013 26×(PGA)2.062 5 (2) (3) 将式(1)、(2)分别代入式(3)即可得各损坏状态的概率分布函数,以最长立柱A1中度损坏为例,取立柱底部的曲率为16×10-3,得到该状态下的概率分布函数如下: Pf=Φ[In(0.029 02×(PGA)1.587 7/(0.016)1/2] (4) 取不同的地面峰值加速度PGA和不同状态的曲率φ,从而绘制出易损曲线,见图18~19所示。对比分析可知:(1)不同损坏状态对应的超越概率,SC1立柱和SC5立柱都随PGA的增大而增加,即拱上立柱的易损性随着PGA的增大而呈现递增趋势。(2)与IDA分析结果类似,长柱和短柱的易损性曲线差异明显,以PGA=0.50g为例进行对比:当PGA=0.5g时,长柱发生轻微损坏、中度损坏、严重损坏和倒塌的超越概率分别为99.45%、15.62%、0.03%和0.01%,短柱对应的超越概率则为60.26%、0.01%、0.00%和0.00%,说明SC1立柱的破坏概率明显更高,即SC5立柱的抗震性能更优。(3)拱上立柱发生轻微损坏、中度损坏和严重损坏的易损线曲线间隔较大,说明在特定强度的地震动激励下,拱上立柱发生不同破坏状态的概率差别也较大。 图18 SC1立柱易损性曲线Fig.18 Fragility curve of of spandrel column SC1 图19 SC5立柱易损性曲线Fig.19 Fragility curve of of spandrel column SC5 套箍加固后SC1柱的易损曲线见图20所示。对图分析可知:随着PGA的增加,套箍加固立柱发生轻微损坏的超越概率也呈上升趋势。对于加固后的立柱,当PGA小于1.5g时,立柱几乎不发生中度损坏、严重损坏和倒塌,这与立柱底部曲率的IDA曲线和分位曲线是一致的。与未加固的SC1立柱对比,对于相同强度的地震动,其超越概率大大降低,说明加固后立柱易损性降低,抗震性能显著提高。 图20 加固后SC1立柱易损性曲线Fig.20 Fragility curve of spandrel column SC1 strengthened by jackets 本文结合德阳金花大桥实际震害,并通过增量动量分析,建立基于IDA的钢筋混凝土套箍加固拱上立柱抗震性能评估分析方法。结果分析可知,长立柱与短立柱的抗震性能差异显著,长立柱的抗震性能相对较差,其易损性明显大于短立柱。采用套箍加固后立柱其抗震性能大大提高,易损性明显降低,延性亦有明显改善。通过本文研究对其他类似桥梁震后承载能力评定具有一定的指导意义。

3 计算结果及分析
3.1 损伤指标DM的选取


3.2 拱上立柱IDA曲线



3.3 既有立柱抗震性能评估



3.4 套箍加固立柱抗震性能评估
4 结论
