季节冻土区土钉支护边坡地震反应动力特性分析

陈 兵, 吴晓磊, 董建华, 何鹏飞

(1. 甘肃天水绿色装配式建筑产业发展有限公司, 甘肃 天水 741000;2. 兰州理工大学 土木工程学院, 甘肃 兰州 730050;3. 兰州理工大学 理学院, 甘肃 兰州 730050)

0 引言

我国冻土分布广阔,其中季节冻土区面积约514万km2,占我国土面积的55%左右,广泛分布于东北、华北、西北等地区[1]。近几年随着寒区经济建设的快速发展,在这些季节冻土区建造了许多重要的基础工程,如哈尔滨—大连高速公路、哈佳铁路工程、新疆油气管网建设工程等,这些工程建设过程中不可避免地会穿过高山地带,遇到许多路堑人工边坡或自然斜坡,由于这些季节冻土边坡受到季节冻融作用极易发生滑塌失稳破坏。此外,这些季节冻土区存在许多大而密集的地层活动断裂带,地震频繁发生,如1986年黑龙江省德都5.5级地震、2010年青海玉树7.1级地震、2021年玛多7.4级地震等[2]。这些高烈度地震又会进一步加剧季节冻土边坡失稳破坏的可能性[3],因此,如何使得季节冻土边坡在地震荷载作用下的长期安全稳定成为工程师们逐渐关注的问题。

土钉柔性支护结构由于具有良好的加固支护力学性能,价格低廉,施工方便容易等优点而常常被国内外广泛用于融土地区的工程地质灾害预防[4]。此外,由于土钉具有一定柔性,相比刚性挡墙等刚性支护结构能在一定程度上减小冻胀力,故近几年土钉也逐渐应用在季节冻土边坡防护工程中。

目前,学者们已对土钉这种柔性支护结构进行了一定的研究,取得了有益的成果。在融土区动力方面:El Emam等[5]进行了五次振动台试验,得出的结论是增加钢筋长度有助于减少连接荷载、墙位移。董建华等[6-7]建立了土钉支护边坡动力计算模型,并给出了理论解析解,通过数值模拟对其进行了验证。邓东平等[8]开展了地震作用下的土钉拟静力分析,并结合算例对其进行了参数影响因素研究。在冻土区方面:张媛等[9]通过对有限元软件二次开发,研究了土钉支护季节冻土边坡时的冻融反应。陈默等[10]通过北京某越冬基坑工程实例,分析了冻胀力对土钉支护基坑稳定性的影响。郭红仙等[11]探讨了冬季气温降低时对土钉支护力学性能的影响,并给出冬季设计和施工时应该注意的要点。

尽管以往关于土钉支护结构静动力学特性的研究取得了一定的成果,然而这些研究一方面大多是关于传统融土边坡土钉支护结构的动力分析,没有考虑季节冻融作用对其动力特性的影响,另一方面主要关于冻土边坡土钉支护结构静力学研究,没考虑到地震荷载的作用。因此,开展地震荷载作用下土钉支护季节冻土边坡地震响应研究是很有必要的。

本文结合有限元软件ABAQUS中的热学和动力学模块,采用黏弹性动力人工边界条件,建立了季节冻土区土钉边坡支护结构的有限元模型,实现了热-动力耦合分析。同时还研究了在夏季和冬季这两个典型季节时刻的不同加速度峰值作用下的地震动力响应并进行了对比分析。本文的研究有助于更好地了解季节冻土区土钉支护边坡的抗震性能。

1 热-动力模型控制方程

1.1 温度场控制方程

冻结区:

(1)

未冻区:

(2)

式中:f、u分别表示冻结和融化状态;Tf、Cf、λf分别为冻结区内土体的温度、体积热容和导热系数;t为时间;下标为“u”者均为未冻区内的相应物理量。

在冻融分界面m上,满足斯蒂芬条件[12]:

(3)

式中:L为相变潜热;ω为土体含水量;ρ为土体密度;ηm为冻融界面m上的单位矢量。

由于冻融交界面存在大量的放热和吸热,属于强非线性数学问题,故本文基于焓模型的相变温度场方程:

(4)

采用伽辽金法和虚功原理对上述方程进行推导,可得出矩阵形式的温度场有限元方程组[13]:

(5)

式中:[K]为温度刚度矩阵;[N]为非稳态焓场刚度矩阵;{P}为荷载合成列阵。

1.2 动力控制方程

动力作用下单元体所受体力:

(6)

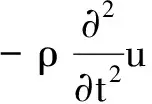
考虑不同结构单元节点上作用的力,建立整个土钉支护季节冻土边坡结构的动力平衡方程,得到:

[M]{u″}+[C]{u′}+[K]{u}={F}

(7)

式中:[M]为结构的整体质量矩阵;[C]为结构的整体阻尼矩阵;[K]为结构的整体刚度矩阵;{F}为结构的节点荷载列阵;{u″}结构的节点加速度列阵;{u′}为结构的节点速度列阵;{u}为结构的节点位移列阵。

其中:

[C]=α[M]+β[K]

(8)

式中:α、β分别是质量矩阵系数和刚度矩阵系数。根据振型正交条件,α、β与振型的阻尼比、振型的固有频率可以建立如下关系:

(9)

结合式(8)、(9)可以求出瑞利阻尼模型参数α、β分别为:

(10)

式中:ωi、ωj分别为结构第i、j振型的固有频率;ξi、ξj分别为结构第i、j振型对应的阻尼比。

2 有限元数值模型建立

2.1 土钉支护季节冻土边坡模型

设西北地区某季节冻土边坡的坡体高度为7.5 m,共设置4排土钉对其进行支护,上两排的土钉长度为7 m,下两排的土钉长度为6 m,该边坡土质为粉质黏土,土钉密度为2 100 kg/m3,等效弹性模量及泊松比分别为220 000 MPa、0.26。此外,季节冻土边坡土体在夏季和冬季时会出现季节冻融层,本数值模型中的季节冻土和融土均采用摩尔库伦弹塑性模型,根据土钉受力特点,将数值模型中的土钉采用Truss杆单元模型,季节冻土边坡采用实体单元。土钉与季节冻土边坡坡体之间的接触面设置为库仑摩擦接触单元,土钉与土体之间的摩擦系数取0.63,其几何模型及有限元网格图如图1、2所示。

图1 土钉支护路堑边坡几何模型图Fig.1 Geometric model diagram of cut slope supported by soil nailing

本文对土钉支护季节冻土边坡进行热动力耦合分析时,首先输入季节冻土边坡的土体在冻结和融化状态下的各种热学参数(表1)及温度边界条件进行热学分析,然后采用与温度场分析相同的有限元网格,将典型季节时刻的温度场导出作为动力分析时的预定义场,同时在材料模块将力学参数与温度相关联,二者关系采用式(11)表示[14-16]。这样就保证了地震动力特性分析采用的力学参数是与预定义温度场是相关的,即分别将不同季节时刻的温度场作为动力分析时的预定义场后再进行动力响应分析,实现了对

表1 土体不同状态物理力学参数

土钉支护季节冻土边坡的热-动力耦合分析。

土体弹性模量、泊松比以及抗剪强度与温度的关系可用下面的公式所表示:

(11)

式中:ai、bi均为试验常数[17-19],当土温大于0 ℃时,bi均为 0;T为土体温度;m通常取0.6。

2.2 边界条件施加

当进行热学分析时,坡底、坡面及坡顶施加西北季节冻土区气温边界:T=11.24+22sin(2πt/365+π),模型底部边界给定热流密度0.035 W·m-2·s-1,模型两侧为绝热边界,相变区间取-0.15～0.1 ℃,模型初始温度取-2.2 ℃。当进行动力学分析时,为了更好地模拟地震波的传播过程,模型四周设置黏弹性人工边界条件(如图2所示),底部通过施加地震波加速度时程曲线,表2为以往学者给出的人工边界节点单位影响面积时的弹簧刚度和阻尼系数取值建议。为了对实际地震波的波动问题进行合理模拟,故需要对黏弹性人工边界上的弹簧-阻尼元件的弹簧刚度和阻尼系数进行合理的设置[20]。

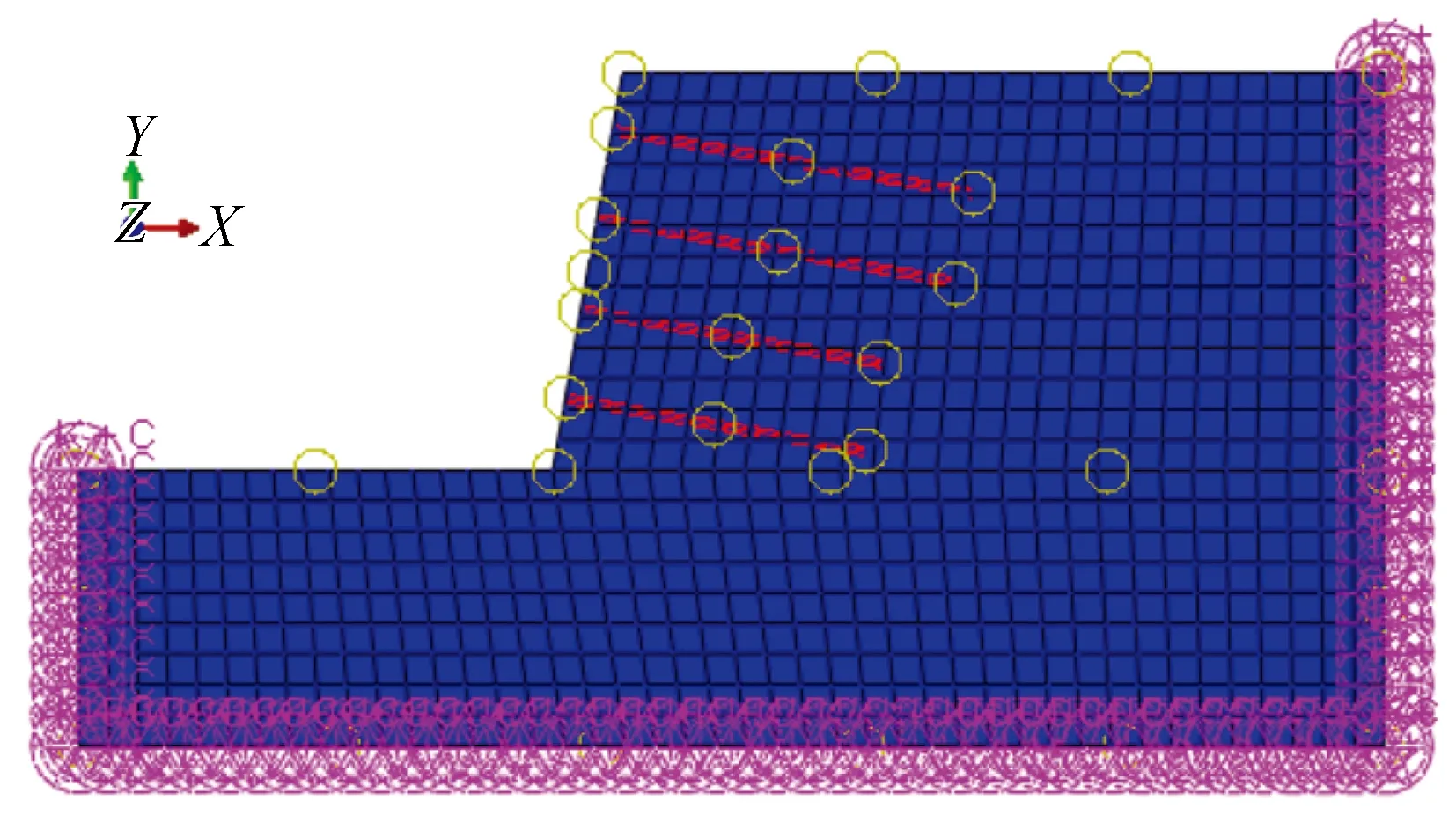
图2 有限元网格图及黏弹性边界条件Fig.2 Finite element mesh diagram and viscoelastic boundary conditions

表2 刚度系数和阻尼系数计算公式

其中:

(12)

式中:CBN为人工边界节点法向阻尼系数;CBT为人工边界节点切向阻尼系数;E为介质的弹性模量;KBN为人工边界节点法向弹簧刚度;KBT为人工边界节点切向弹簧刚度;G为介质剪切模量;ρ为介质密度。

2.3 地震波类型的选取及加载工况

本文土钉支护季节冻土边坡的地震动力数值模型选用EI Centro地震波作为该模型的水平地震加载波。根据抗震设计规范规定,并以峰值加速度为0.1g、0.2g、0.4g(对应规范中的抗震烈度为7、8、9度)在模型底部进行地震波加载,当激震地震全时段模拟完成后,对提取特定部位的地震波应进行处理。图3为输入EI Centro地震波的加速度时程。

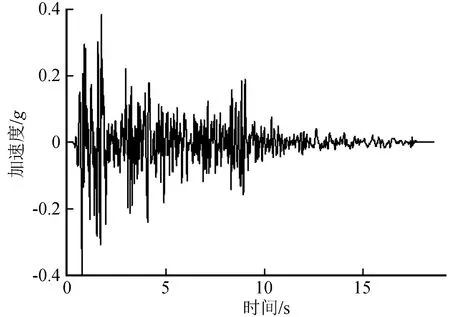
图3 EI Centro地震波时程曲线Fig.3 Time history curve of EI Centro seismic wave

3 季节冻土区土钉支护边坡地震动力响应分析

本文分别对土钉支护季节冻土边坡在峰值加速度为0.1g、0.2g、0.4g时的加速度动力响应、位移动力响应以及土钉轴力动力响应开展有限元计算并进行动力响应对比分析。

3.1 动加速度响应

图4为EI Centro地震波在峰值加速度为0.1g～0.4g激振下冬季和夏季典型季节时的加速度动力响应对比云图。从图中可知,当输入0.1g的EI Centro地震波时,夏季时刻从季节冻土边坡坡底至坡顶的加速度响应范围为-61.7 ～-153.1 cm/s2;冬季时刻从季节冻土边坡坡底至坡顶的加速度响应范围为-66.2～-137.5 cm/s2;当输入加速度峰值为0.4g时的EI Centro地震波时,夏季与冬季时刻的从季节冻土边坡坡底至坡顶的加速度响应范围分别为-285.5～-610.4 cm/s2,-296.2 ～-537.5 cm/s2。故可知冬季时季节冻土区边坡的季节冻融层会完全冻结,刚度比较大,对边坡有一定的保护作用,而夏季时季节冻结层完全融化,从而使得土钉支护季节冻土边坡在相同地震波激振下夏季的加速度反应比冬季时的加速度反应强烈,夏季时的土钉支护季节冻土边坡更容易发生破坏。

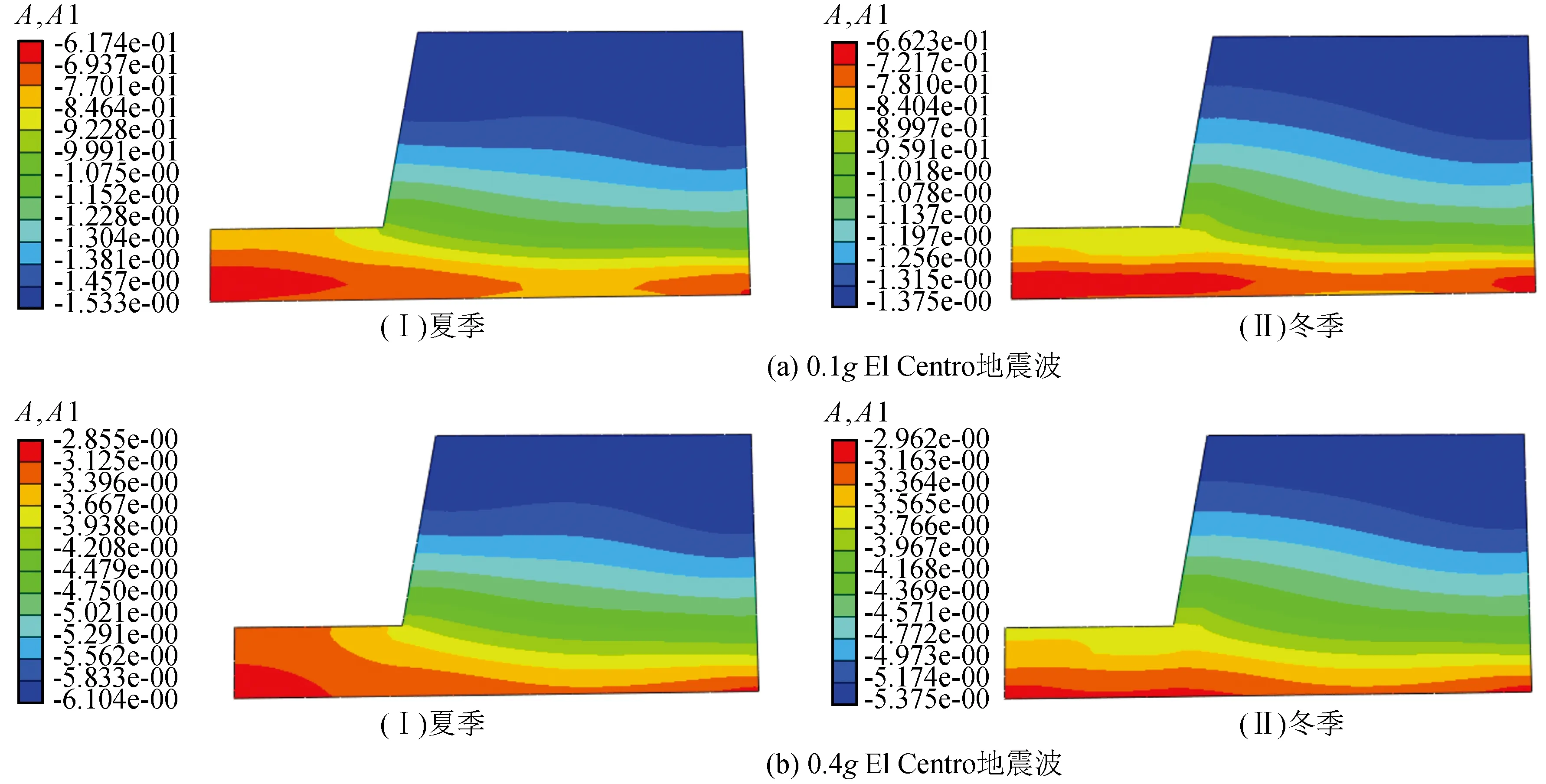
图4 冬季和夏季时期在EI Centro地震波不同峰值加速度激振下的加速度动力响应云图Fig.4 Cloud diagram of acceleration dynamic response under the excitation of EI Centro seismic wave with different peak acceleration in winter and summer

图5为EI Centro地震波在不同的峰值加速度激振下坡底、坡面及坡顶不同高程处的加速度时程曲线对比图。从图中可知,土钉支护季节冻土边坡不同部位处的加速度时程曲线大致趋势基本一致,与输入的地震波加速度时程曲线相似。同时土钉支护季节冻土边坡的坡面加速度峰值比坡底大,坡顶位置处的加速度峰值达到最大,表明地震波加速度峰值随着土钉支护季节冻土边坡的坡高度增加而增

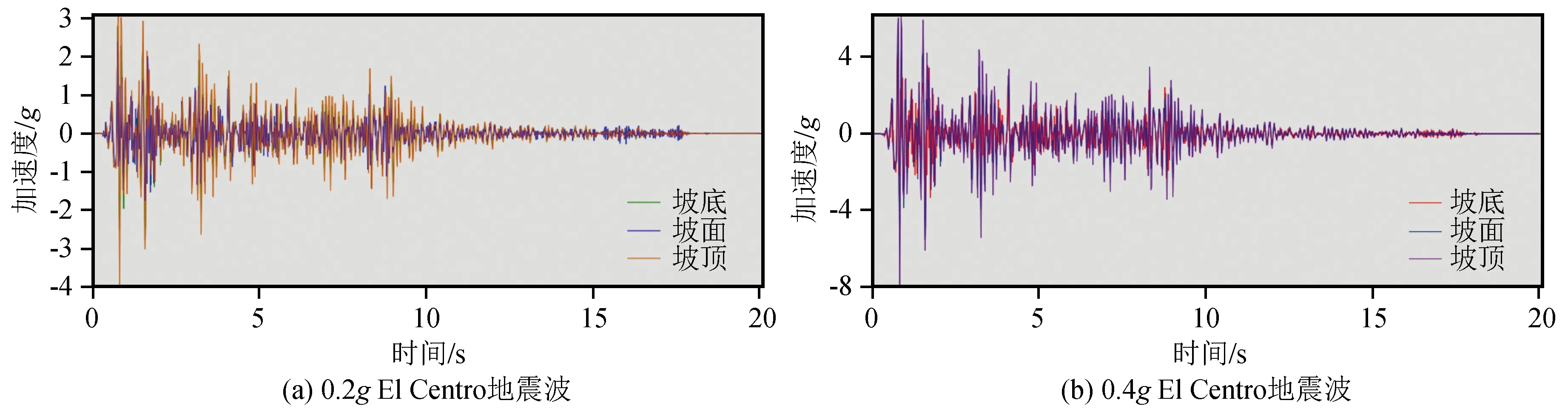
图5 坡底、坡面及坡顶不同高程处的加速度时程曲线对比图Fig.5 Comparison of acceleration time history curves at different elevations of slope bottom,slope surface and slope top

加,具有明显的高程放大效应。故应对坡顶位置处的土钉应加强处理,防止夏季地震发生时该位置发生毁坏。

3.2 动位移响应

图6为在EI Centro地震波在峰值加速度为0.1g～0.4g激振下典型时间点的位移动力响应云图。从图中可知,当输入0.1g的EI Centro地震波时,夏季时刻从季节冻土边坡坡底至坡顶的位移响应范围为-1.54×10-4～2.0×10-4m;而冬季时刻为-1.39×10-4～9.38×10-5m;当输入加速度峰值为0.4g时的EI Centro地震波时,夏季与冬季时刻的从季节冻土边坡坡底至坡顶的位移响应范围分别为1.82×10-3～2.22×10-3m,1.20×10-3～1.37×10-3m。位移响应云图随着季节冻土边坡高度均呈现出颜色顺序逐层变化,且每层^颜色呈条状分布,即每层位移响应大致相同,这是因为土钉对季节冻土边坡起到了加固作用。此外,通过对比夏季和冬季时的位移峰值后还可看出,同一强度的地震波激振下,冬季时刻的位移明显比夏季的小,这是因为冬季时边坡季节活动层会冻结形成刚度比较大的硬壳层,相当于对坡内未冻结土体具有一定的约束作用,限制其在地震作用下发生运动,从而使得夏季时刻土钉支护边坡的地震动位移比冬季的稍大一些。

图6 冬季和夏季时期在EI Centro地震波不同峰值加速度激振下的位移动力响应云图Fig.6 Cloud map of displacement dynamic response under the excitation of EI Centro seismic wave with different peak acceleration

图7为在EI Centro地震波在峰值加速度为0.1g～0.4g激振下典型时间点的位移时程曲线对比图。从图中可知,从土钉支护季节冻土边坡的坡底至坡顶的位移峰值逐渐增大,且与加速度动力响应变化规律相似,表明位移动力响应也同样随着高程增大而增大,具有高程放大效应

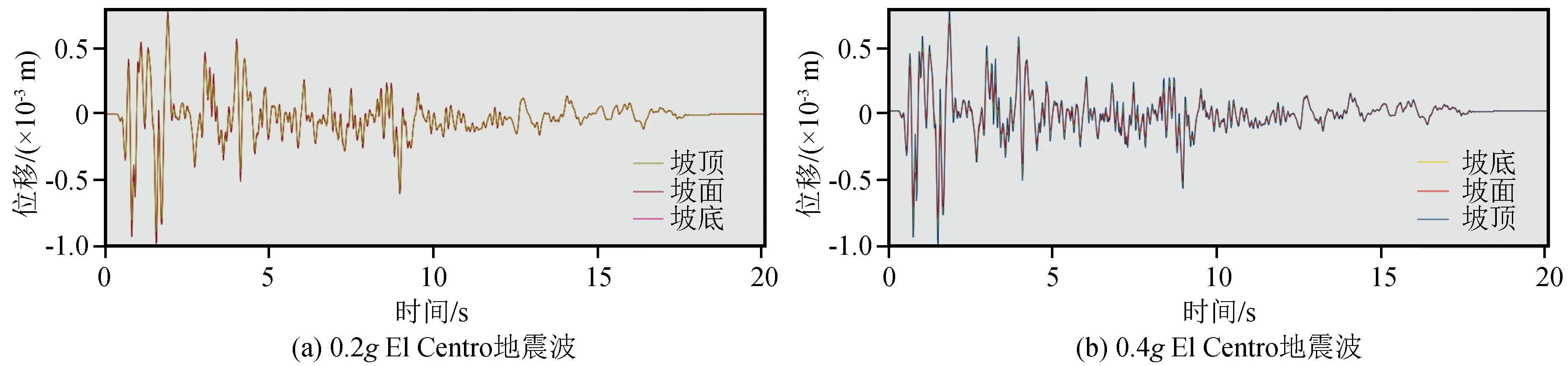
图7 坡底、坡面及坡顶不同高程处的位移时程曲线对比图Fig.7 Comparison diagram of displacement time-history curves at different elevations of slope bottom,slope surface and slope top

3.3 土钉轴力响应

图8为在EI Centro地震波在峰值加速度为0.4g激振下不同时期的土钉轴力动力响应云图。从图中可知,在EI Centro地震波激振下,从季节冻土边坡的坡底至坡顶的土钉端部轴力峰值逐渐增大,在夏季时刻坡顶位置处的土钉钉头轴力比较大,表明土钉钉头轴力也具有高程放大效应和季节变化效应。

图8 夏季和冬季时刻EI Centro作用下不同峰值加速度激振下的土钉轴力响应云图Fig.8 Cloud diagram of axial force response of soil nailing under the excitation of EI Centro seismic wave with different peak acceleration in winter and summer

4 结论

本文基于季节冻土边坡特征,通过非线性有限元软件ABAQUS热动力分析模块建立了地震荷载作用下土钉支护季节冻土边坡地震动力响应数值模型,并在模型边界处添加了黏弹性人工边界。对其加速度、位移动力响应以及土钉轴力响应进行了分析,得到以下主要结论:

(1) 不同地震波峰值加速度作用下,土钉支护季节冻土边坡的不同位置处的加速度动力响应具有高程放大效应和季节变化效应,在夏季时刻的季节冻土边坡坡顶位置处加速度响应峰值最大,在边坡位置处加速度响应峰值最小。此外,加速度峰值随着地震波激振加速度峰值增大而增大。

(2) 无论是夏季还是冬季,地震动位移响应云图大体相似,且呈现出不同程度的分层现象,同样位移响应也随着地震波激振峰值增大而增大。表明高烈度地震对土钉支护季节冻土边坡破坏性较大。

(3) 土钉钉头轴力具有高程放大效应和坡面放大效应,从季节冻土边坡的坡底至坡顶的不同季节时刻的土钉端部轴力峰值逐渐增大。

(4) 本文虽然通过数值软件中的热力耦合模块分析了土钉支护季节冻土边坡的地震动力响应,对以往研究做了一定的推进,但这些结论大多依赖数值计算得出的,缺乏相关的动力试验验证。因此,为了将来可以更为深入和更贴近真实地了解季节冻土区土钉支护边坡的地震动力响应特性和破坏模式,可开展季节冻土区土钉支护边坡的大型振动台地震动力模型试验研究,进一步研究不同季节时期土钉支护边坡的渐进破坏特性和破坏模式等。