大功率鼠笼式异步电动机起动瞬态温升计算
2021-10-26李少斌李建富史庆夫
李少斌 李建富 史庆夫
(东方电气集团东方电机有限公司,四川618000)
鼠笼式异步电动机由于结构简单、运行可靠、易于空载的优点,广泛应用于厂矿企业、交通运输及农业生产等领域[1]。大功率鼠笼式异步电动机,其轴系转动惯量较大,且阻力矩较大,起动困难。为提高起动转矩,部分机型采用全压直接起动方式。即使这样,起动时间仍长达数十秒,直接起动产生严重的集肤效应和起动电流,在转子上产生很大的损耗,引起转子温度迅速升高,导致电机转子在起动过程中发热问题突出,最高可达300 K以上,产生巨大的热应力,在离心力的共同作用下,严重时甚至可能会损坏电机转子,引起电机故障。因此,温升问题是大功率鼠笼式异步电动机安全运行的关键,准确、快速的起动温升计算方法是开发高性能异步电动机的关键。
对于异步电机的起动问题,国内外研究者已经开展了不少研究[2-5]。但这些研究都是针对中小容量电机,对于容量5 MW以上、转动惯量达3000 kg·m2以上的大容量异步电动机来说,起动温升问题尤为突出,需要单独研究。
针对大功率鼠笼式异步电动机的起动温升问题,本文以某项目5000 kW、4P鼠笼式异步电动机样机为研究对象,分别采用更能真实反映电机暂态起动过程的全瞬态有限元法和具有更小计算量的频域有限元半解析法,对样机的起动过程进行仿真分析,对两种方法的精度和计算时间进行综合对比分析。
1 有限元仿真计算方法
1.1 电机电磁计算数学模型
针对鼠笼式异步电动机的起动问题,计算可基于如下假设条件[6-7]:
(1)定子绕组中电流均匀分布;
(2)忽略铁心磁滞效应,材料为各向同性。
鼠笼式异步电动机有限元电磁计算求解域如图1所示。
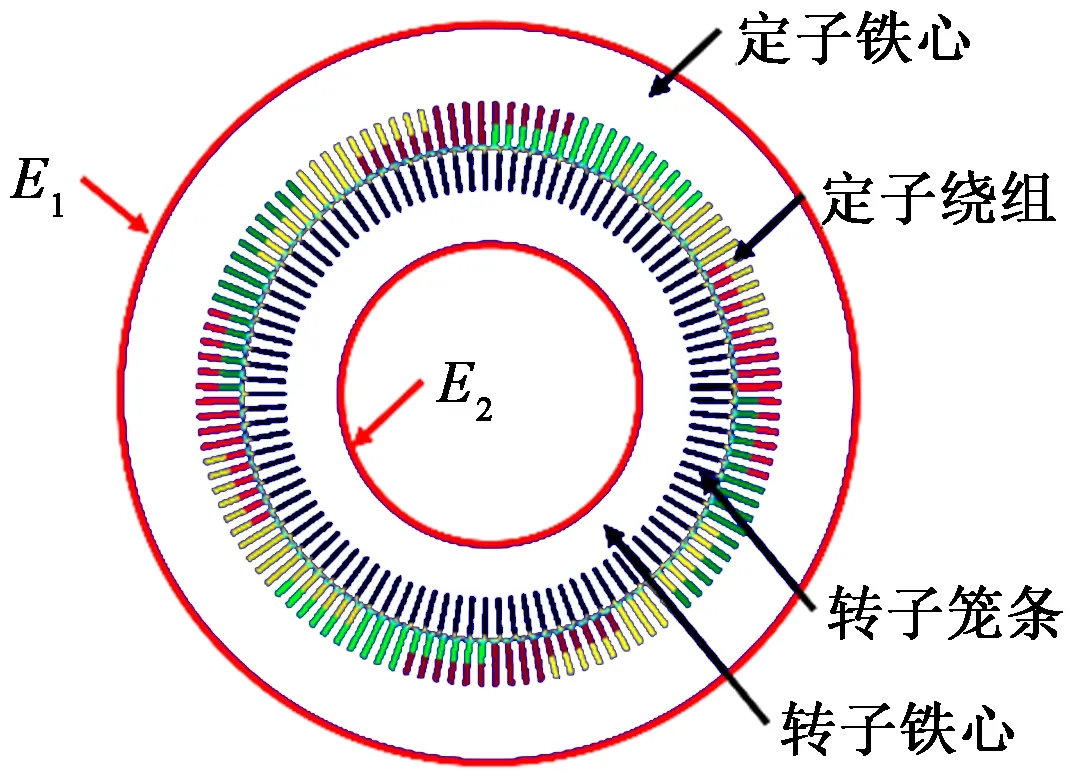
图1 鼠笼式异步电机求解域
求解域内满足[6-7]:
(1)
A=0 (在边界E1、E2上)
(2)
式中,A为矢量磁位;φ为标量磁位,v为磁阻率,Js为电流密度。
1.2 鼠笼式异步电动机有限元模型
采用的5000 kW鼠笼式异步电动机基本参数见表1,建立的有限元模型与剖分见图2。
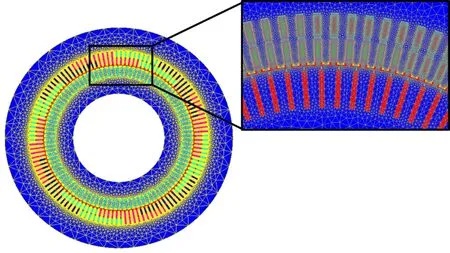
图2 5000 kW鼠笼式异步电动机有限元模型

表1 鼠笼式异步电动机基本参数
采用场路耦合方法,电机的耦合电路如图3(a)所示,鼠笼内部的电路如图3(b)所示。
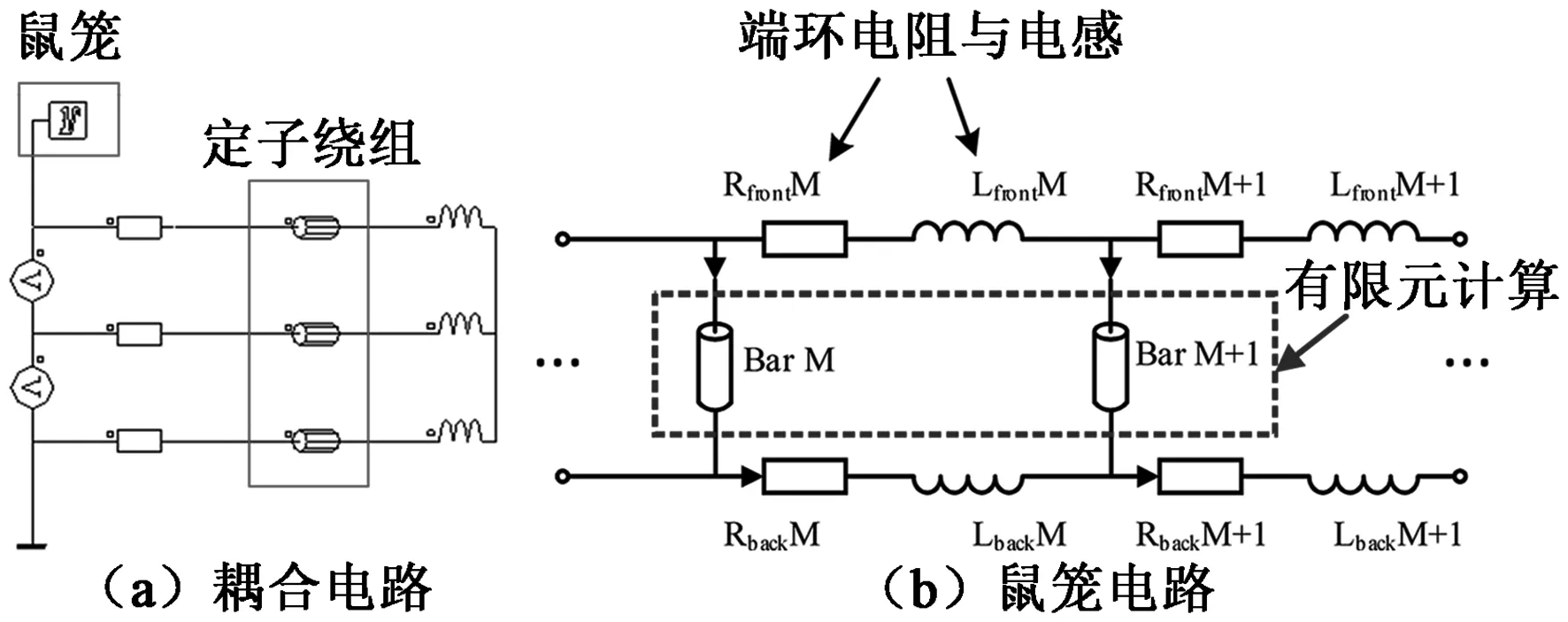
图3 5000 kW鼠笼式异步电动机外电路
笼条部分采用有限元计算,考虑槽漏磁引起的集肤效应;而端环的电阻和电感由集中参数表示,进行电路计算。通过有限元法计算解出电流密度Jz后,可算出谐波影响与集肤效应的导条区域涡流损耗为:
(3)
式中,Jz为导条某单元内计及谐波影响的电流密度;Δe为该单元面;ρ为笼条电阻率;le为笼条有效长度。
电机起动过程的温升可按照绝热过程近似计算:
θ=Q/cm
(4)
式中,θ为温升;Q为损耗产生的热量;c为材料的比热;m为材料质量。
2 起动温升计算方法及对比分析
2.1 起动温升计算方法
鼠笼异步电机起动时间是一个涉及电磁感应和机械耦合作用的瞬态过程,计算复杂度高,产生误差因素较多。为了平衡计算精度和计算时间,分别采用频域有限元半解析法和全瞬态有限元法两种方法对5000 kW鼠笼式异步电动机起动过程及温升进行计算,并对结果精度、计算时间进行综合对比分析。
其中,频域有限元半解析法是指利用电磁场有限元的稳态频域计算结果得到T-S曲线,结合已知的阻力特性曲线,再根据机械运动方程,可以半解析地计算出电机的转动加速度,进而得到电机起动加速曲线:
(5)
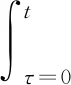
(6)
式中,α为转动加速度;Ta为电机加速转矩;Te为电机的电磁转矩;Td为电机及负载的阻力矩;J为转子及负载的转动惯量;n为转速;t为时间。
这种方式只需计算稳态的频域有限元,计算量较小,求解速度快。例如本文所研究的5000 kW鼠笼式异步电动机样机,采用CPU i7-8700、内存32 GB的小型工作站进行计算,仿真总共耗时约10 h。
全瞬态有限元法是指直接采用时域有限元计算,将机械方程直接耦合在时域有限元中,每个时间步都会计算出当前的瞬时电磁转矩和转速、涡流分布,理论上精确度更高,但计算量非常大。例如本文采用的样机,起动时间需要15 s左右,每个电周期20个时步,计算整个起动过程需要约15 000个时步,采用CPU i7-8700、内存32 GB的小型工作站进行计算,仿真总共耗时约430 h。
2.2 计算结果及对比分析
采用频域有限元半解析法,电机阻力矩曲线以及由频域有限元法计算得到的T-S曲线如图4所示,根据机械运动方程解析计算得到的加速转矩和转速曲线如图5所示,从图5可以看出,电机起动时间为13.5 s。

图4 阻力矩和电磁转矩T-S曲线
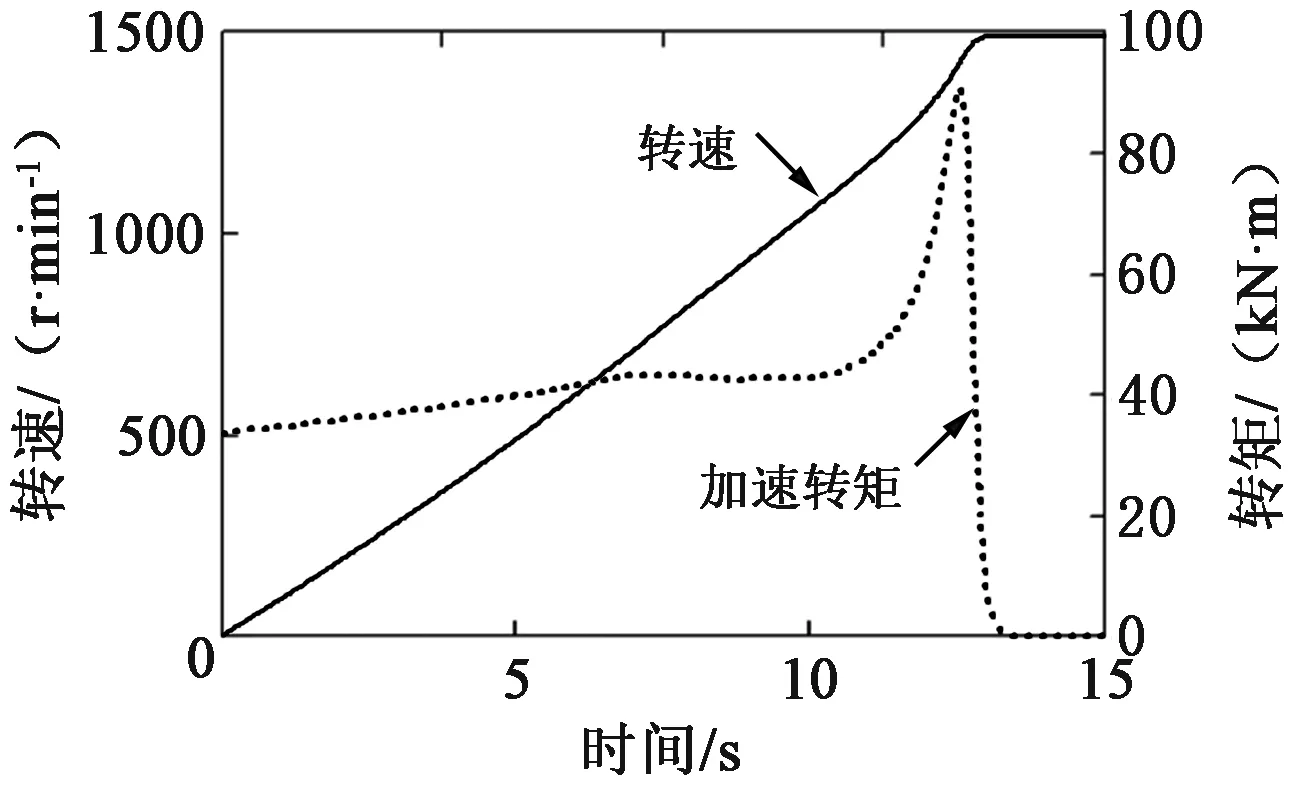
图5 加速转矩和转速上升曲线
采用全瞬态有限元法得到的转速上升曲线和频域有限元半解析法所得结果对比如图6所示。
从图6可以看出,全瞬态有限元法得到加速曲线在电机开始起动时上升较为缓慢,但在2 s左右开始迅速增大,最终得到的起动时间为12.6 s,比频域有限元半解析法得到的起动时间短0.9 s。
采用两种方法所得计算结果对比见表2,其中,起动温升是根据笼条的损耗,按照公式(4)计算得到的。从表2可以看出,两种方法得到的起动时间和起动温升两个参数分别偏差7.1%和9.2%。

表2 不同方法起动计算结果对比
从上述对比结果来看,采用全瞬态有限元法和频域有限元半解析两种方法计算的异步电机起动过程存在一定差别,起动时间、温升偏差分别为7.1%、9.2%。这些差别是由于全瞬态有限元法完整的模拟了电机启动的动态过程,计及了电流中各种非周期、谐波分量带来的影响;而频域有限元半解析法是把起动过程的每个时间点都看作是一个稳态计算,忽略了瞬态电流中的非周期性分量带来的电磁转矩的振荡以及一部分谐波的影响。而全瞬态有限元法计算耗时超过频域有限元半解析法耗时的40倍。因此,在对计算时间敏感且精度要求不太高的场合,可以采用频域有限元半解析法计算和分析异步电机起动温升问题。
3 结论
通过建立5000 kW鼠笼式异步电动机的有限元模型,分别采用频域有限元半解析法和全瞬态有限元法,对其起动过程进行仿真,并计算起动温升。对比分析表明:
由于大型鼠笼式异步电机转动惯量大,起动时间长,采用全瞬态有限元法仿真起动过程计算量非常大,耗时约430 h;采用频域有限元半解析法计算起动过程,计算量大幅减小,仅耗时10 h,约为全瞬态有限元法的2.3%。
虽然频域有限元半解析法不能计及起动过程中电流非周期、谐波分量的影响,存在一定误差,但是起动时间、起动温升两个关键参数的计算结果和全瞬态有限元法仅相差7.1%、9.2%。考虑到计算效率上的巨大差异,频域有限元半解析法在对结果精度要求不太高时具有一定的工程实用价值。
