一种新型测量气体粘滞系数的装置及实验
2021-10-26谢谦
谢 谦
(商洛学院 电子信息与电气工程学院,商洛726000)
粘滞系数是表征流体性质的重要物理量,在现行的大学物理实验中,对液体的粘滞系数描述较多,而对气体的粘滞系数涉及甚少[1]。这是因为气体的粘滞系数较液体小得多,而且随温度变化不明显,从而给测量带来了一定的难度,特别是气体温度和压强较大时更是如此[2-3]。目前有通过动力学方法[4-5]测定气体的粘滞系数,但气体种类仅限于空气。如何设计出一种较好的装置,通过测量一些宏观量而不是微观量[6-8],从而简便地求出气体的粘滞系数,具有一定的现实意义。由于气体本身的特性,如流动性好、可压缩性好等,因此,本文用来测量气体(以CO2为例)粘滞系数的方法,即用烧瓶内的气体沿水平细圆管排气的实验装置,正是根据气体流动性好这一特点,推导出气体粘滞系数的理论公式,测出相关宏观物理量,代入公式就可以计算出粘滞系数。设计实验对CO2气体的粘滞系数进行了测量并分析结果,表明了该方法具有较高的测量精度。
1 模型设计与建立
1.1 模型设计
如图1所示,把待测气体充入容积为V0的烧瓶中,使其压强pb大于外界大气压强p0,其温度则与外界温度T0一致。烧瓶口外左侧连接一U 型气压计,右侧连接长为L、半径为r 的水平细圆管与大气相通。细管与烧瓶连接处有阀门,先关闭。打开阀门后,瓶内气体经细管向外流出,经过Δt 时间后再将阀门关闭,测出瓶内气体的压强为pe,由此便可确定该气体的粘滞系数η。这整个过程中,烧瓶、细管、外界处处温度相同且保持不变。
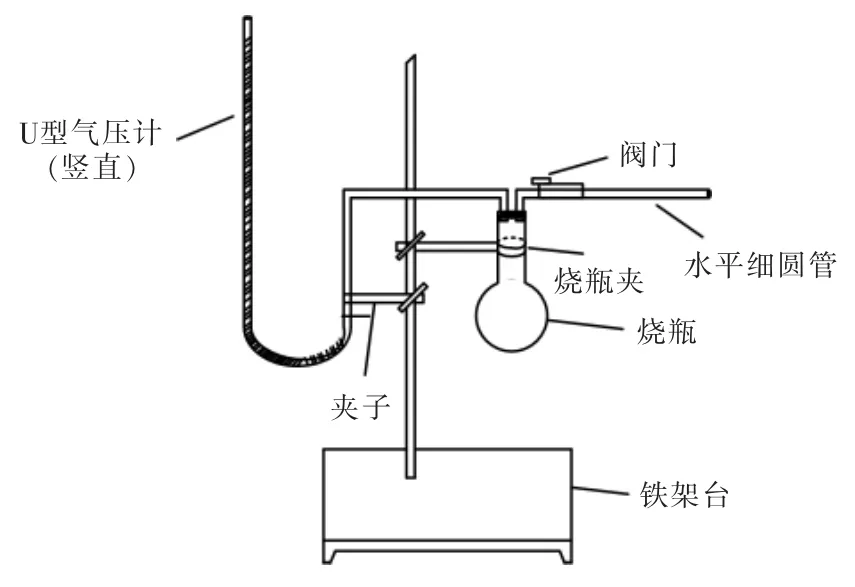
图1 装置模型示意图Fig.1 Diagram of device model
1.2 模型分析
烧瓶内的气体经细管向外流出,气体粘滞性的大小将影响流出的快慢。在同样的时间内,η 越大,流出的气体质量应越小,及终态的气体压强pe应越大。因此,在其他量都确定的前提下,有可能通过pe的测量来确定η 值。本文设计的测量实验,原则上是可行的。
尽管如此,实验设计的过程仍相当复杂。这就要求采用一系列大体上符合实验题型的简化假设和模型,否则理论分析就无法进行,具体分析如下所述。
瓶内气体的体积和温度不变,随着气体从瓶口经细管流出,瓶内气体的质量、密度、特别是压强都将逐渐减少,其变化取决于气体经瓶口流出的体积流量为VQ(单位时间从瓶口流出的气体体积)。假设瓶内气体为理想气体,利用其状态方程可给出瓶内气体压强的变化与VQ的关系。
再看水平细圆管内的气体,与瓶口相连的细管入口处的气体压强就是瓶内气体的压强p,与大气相连的细管出口处的气体压强则为大气压强p0,可见细管内各处的气体压强从而气体密度是逐渐变化的,这表明细管内气体具有可压缩性,否则密度应不变。沿细管取x 轴,取细管内各处气体的压强和密度为px和ρx(即假设细管内任意x 处截面上各点的px相同,ρx相同,忽略压强和密度沿细管径向的变化),对于细管内从x 到(x+dx)的任一小段而言,正是由于px和px+dx的不同,推动了气体沿细管流动。
流体力学中的泊肃叶公式[9]确定了粘滞流体通过细圆管的流量的公式,它指出,当粘滞系数为η的流体流过细圆管时,每秒流过细管中的一圆截面的流体体积为
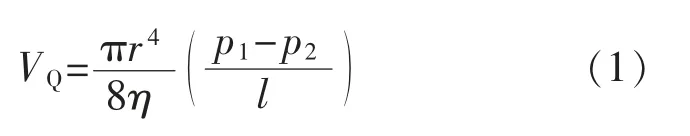
式中:r 和l 是细圆管的半径和长度;p1-p2是细管两端的压强差。泊肃叶公式适用于不可压缩的粘滞流体。在本文中,可把它用于细管中任意dx 小段,即忽略dx 小段气体的可压缩性。由此,可把细管任意x 处的VQ(注意,细管各处VQ不同,应为VQ(x))与前后的压强p 和p0以及η 联系起来。另外,因细管很细并不很长,可以假设在每一时刻管内气体均做稳定流动,即尽管气体密度ρx和流量VQ(x)在管内处处不同,但质量流量ρ(x)VQ(x)却为常量,与x 无关。这样,便可通过积分,把瓶口处的VQ(即VQ(0))与细管两端气体的压强p 和p0以及η 联系起来,这是关键的一步。
2 公式的导出
把以上对瓶内和细管内气体的讨论结合起来,即可顺利导出公式。
设瓶内气体为理想气体。瓶内气体的体积和温度恒定,分别为V0和T0,任意t 时刻瓶内气体的压强、质量、密度分别为p,M,ρ,经瓶口流出的气体的体积流量(即单位时间内经瓶口流出的气体体积)为VQ。由理想气体状态方程:

得出从t 到(t+dt)时间内,气体质量的改变为

由VQ定义,气体流出的质量-dM 与VQ的关系为

由状态方程,得:
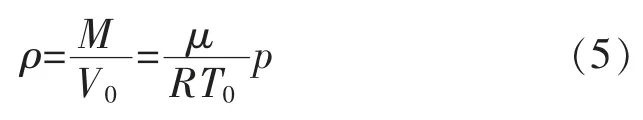
把式(3)、式(5)代入式(4),得:

式中的VQ=VQ(0),见下文。
如图2,沿水平细圆管长度方向建立x 坐标,x=0 处是细管与瓶口连接处,气体的压强为p(即瓶内气体压强);x=L 处是细管与大气相通处,气体压强为p0(即大气压强);任意x 处的气体压强为px。由理想气体状态方程,细管内任意x 处的气体密度ρx为
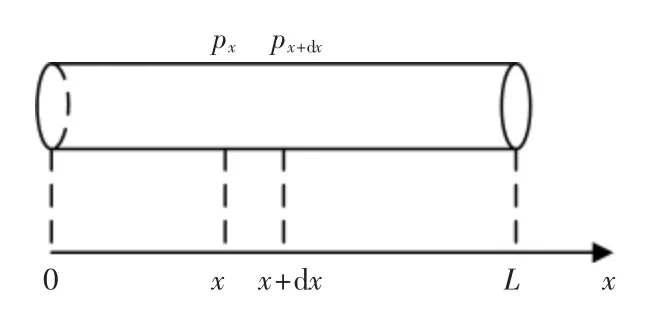
图2 水平细圆管内气体分析Fig.2 Gas analysis in a horizontal fine tube

在细管内任取从x 到(x+dx)的一小段,忽略在此小段内气体的可压缩性。在此小段内气体流速有径向分布,管壁附近流速为零,管轴处流速最大。由粘滞流体在水平圆管中流动的泊肃叶公式,在管中任意x 处,气体的体积流量VQ(x)为
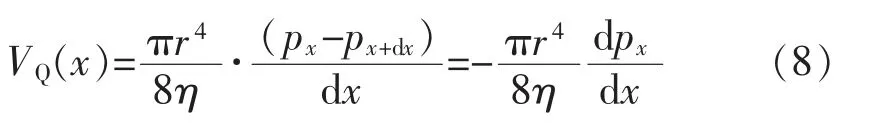
因管细而并不很长,可以认为在每一时刻管内气体近似作稳定流动,即气体的质量流量在管内处处为常量,故

把式(7)、式(8)代入式(9),得:

积分,得:
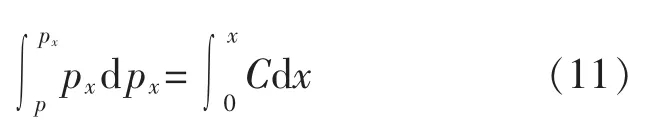
式中p 和px分别是x=0 处和x 处的压强。即:

边界条件为
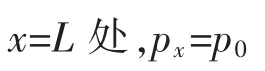
代入,得:

由式(8),x=0 处的体积流量为
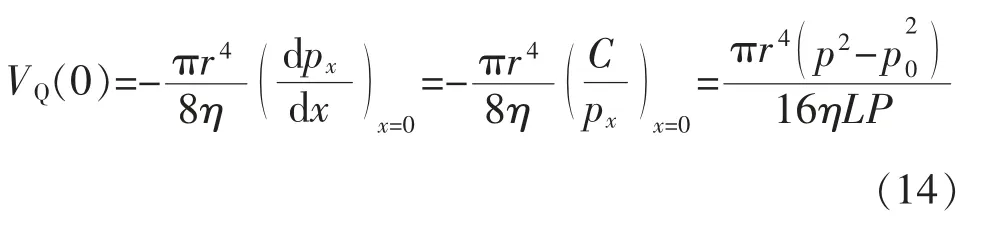
式(14)的VQ(0)就是式(6)的VQ,把式(14)代入式(6),得:
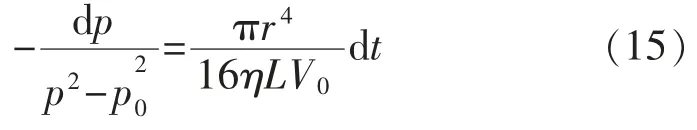
从初态t=0,p=pb到终态t=Δt,p=pe作积分,得:
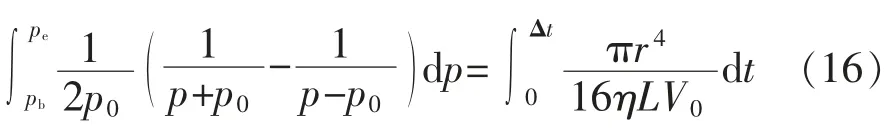
即:
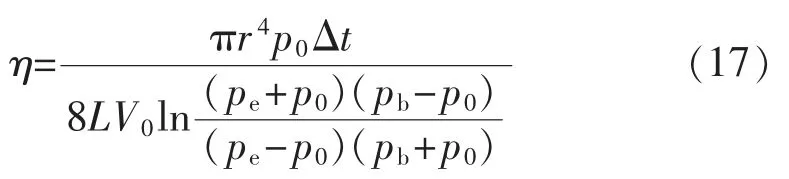
至此,气体粘滞系数公式已全部导出。
3 实验测量与分析
3.1 实验器材
V0=1 L 容积的烧瓶、U 型管气压计、三种内径规格细玻璃管、三种长度规格细玻璃管、移测显微镜、停表、直尺、铁架台等。其中,细管通过试验比较选择长度L=10 cm、内径r=0.050 mm,0.100 mm,0.150 mm 和内径r=0.050 mm、长度L=10 cm,15 cm,20 cm,总共5 根,其中1 根两种情况下共用。
3.2 测量步骤和数据
(1)用直尺和移测显微镜,测量细管的长度和内径;
(2)连接好仪器,在烧瓶中充满CO2,用水银气压计测出瓶中气体初始压强pb,pb=2.11 atm;
(3)打开细管与烧瓶连接处的阀门,放出气体,Δt=22 min 后再次读取水银气压计的示数pe,此即为瓶中气体的末态压强;
(4)用同一内径,不同长度的细管和同一长度不同内径的细管重复步骤(3),得到比较数据;
(5)将相关数据代入式(17),即可算出CO2的粘滞系数η。
由于气体体积V0及初始压强pb和放气时间Δt对粘滞系数之影响很小,所以以上测量数据中V0、pb、Δt 皆不变,影响粘滞系数的只是细管的规格。
3.3 实验数据分析
(1)内径r 相同,而长度L 不同的3 根细管,粘滞系数的实验测量值无明显差异。
(2)通过多次测量可以发现,大、小内径细管测得的气体粘滞系数有一定差别,随着管径的减小,粘滞系数有增大的倾向,这可能是由于管径变小,气体的流量变小,流动性变差的缘故。
(3)两种情况下的实验数据,处理结果分别为
r=0.050 mm 时,η1=(1.415±0.005)×10-5Pa·s,
L=10 cm 时,η2=(1.398±0.013)×10-5Pa·s,
15 ℃时,CO2的粘滞系数η0=1.436×10-5Pa·s,以第一种情况为例,求出其相对误差E=×100%=1.46%
表明该方法测量精度较高。
(4)从以上结果可以看出,影响粘滞系数的主要原因是细管内径,因此要求管内径不能太小,但内径也不要太大,否则气体排出过快,使得终态压强和时间测量误差增大。
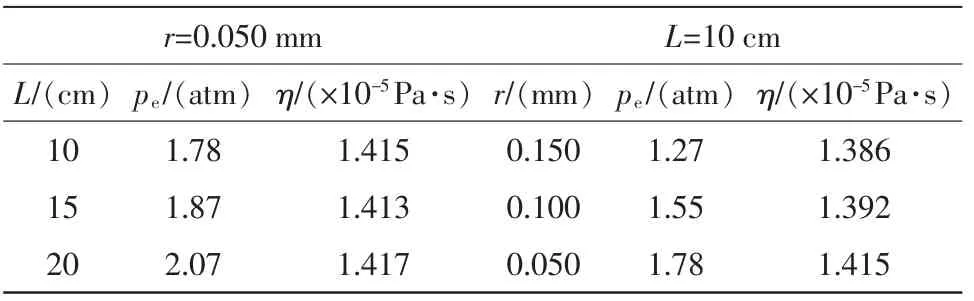
表1 实验测量数据及结果Tab.1 Measurement data and results of experiment
4 结语
本文所提供的模型和装置,不受温度、压强等外界条件的影响,该方法取材方便,操作简便,可以快速准确地测量各种气体的粘滞系数,可以使学生加深对课本内容的理解,获得启迪,对于训练学生的综合实验技能不失为一个有意义的设计性实验,具有一定的推广价值。
