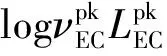平谱射电类星体3C 279的宽带能谱光变特性分析*
2021-10-26孙建圆郭燕飞邓雪娇李海凤高志旭王泽睿谢照华杜雷鸣
孙建圆,郭燕飞,邓雪娇,李海凤,高志旭,王泽睿,谢照华,杜雷鸣
(1. 云南师范大学物理与电子信息学院,云南 昆明 650500;2. 南京大学天文与空间科学学院,江苏 南京 210093)
众所周知,耀变体的一个显著特征是电磁辐射具有大幅度和快速的光变,光变出现在整个电磁波频谱范围内的各个波段,而且还具有由短到长各种不同的时标[1]。了解光变的物理过程能帮助我们更好地理解喷流中辐射区的结构、物理条件的演化以及粒子的加速机制和辐射区位置等重要问题。
目前,引起光变的原因尚不清楚,主要有几种可能的解释[2]:内激波机制、湍流-磁重联机制、几何效应机制和外部因素机制。在内激波机制中,喷流的非均匀性导致了相对论性激波的产生,喷流中传播的激波在波前区将粒子加速,从而产生光变[3-6]。另外,喷流有可能产生湍流,进而可能诱发磁重联[7-11]。磁重联可以产生硬的相对论性电子能谱[12]。还有一种可能的机制是光变的几何效应起源[13-16]。由于在喷流的甚长基线干涉测量技术(Very Long Baseline Interferometry, VLBI)观测中经常看到弯曲或者螺线型的结构,所以这种机制是把光变的主要因素解释为弯曲或者螺线型的喷流路径。因为路径上不同位置的辐射区具有不同的多普勒因子,从而主导了光变。最后一种喷流或者喷流中的高能辐射区通过和外部物质进行直接碰撞或者辐射相互作用而产生光变[17-19]。由于本文主要研究喷流内在的光变物理特性,所以最后这种机制不在本文的考虑范围内。
光变的研究内容包括光变曲线以及从中提取的光变时标,各波段能谱形状在光变过程中的变化,各波段光变曲线之间的相关性、延迟性,光变的周期性、功率谱分析等性质[20-21],还有对光变过程中某个时刻得到的同时/准同时性光谱能量分布的研究[22]。对光谱能量分布的研究由于能通过模型拟合把观测到的光谱能量分布随时间变化的性质和喷流内部物理条件的变化联系起来,为光变过程提供较多的物理信息。以下我们把一个同时/准同时性光谱能量分布数据描述的状态简称为一个 “态”,一次光变过程一般包含若干个态。
自1991年EGRET(the Energetic Gamma-Ray Experiment Telescope)首次探测到λ射线波段以来[23],3C 279成为被观测最频繁的耀变体之一[23-28]。它属于耀变体的一个子类(平谱射电类星体),具有典型的耀变体特征。3C 279有一个明显的射电喷流,在整个电磁波谱中都存在光变。最近,文[28]分析了视界望远镜在20微角秒分辨率下对3C 279内喷流的观测数据,得到3C 279辐射区结构和光变的精细化信息。但是在γ射线波段的分辨率依然不足以直接分辨精细结构,所以关于高能辐射的信息,如辐射区位置等只能用间接推断的方式得到[29]。
由于具有丰富的观测数据,3C 279的光变曾多次作为研究对象[30-34]。截至目前,3C 279的光变研究一般只集中于一次或者数次耀发的个案,或者对某个时段内的数个耀发,而且不同的作者使用的模型不同。如文[30-32]使用双拐折幂律谱电子能谱分布的单区轻子模型分别对2008年8月~2010年8月的8个态和2013年12月~2014年4月的4个态进行了拟合;文[35]使用拐折幂律谱电子能谱分布的单区轻子模型对2014年3月~4月的γ射线波段的耀发事件进行了拟合;文[36]使用拐折幂律谱电子能谱分布的含时轻子强子模型和双区轻子模型对2013年12月的硬γ射线波段的耀发事件进行了拟合;文[37]使用对数抛物谱电子能谱分布的单区轻子模型和单区轻子强子模型对2015年6月的耀发事件进行了拟合;文[38]使用拐折幂律谱电子能谱分布的单区模型对2018年1月的耀发事件进行了拟合;文[39]使用拐折幂律谱电子能谱分布的单区轻子模型对2015年6月中旬的耀发事件进行了拟合;文[33]使用含时单区均匀模型研究了3C 279的16个态,是迄今为止态数量最多的研究。但是这些研究中态的样本数量依然不足以支持有统计意义的分析结果。所以本文搜集了一个含有3C 279共29个态的样本,对该源光变时外在观测和内在物理特性进行统计研究。
1 同时/准同时性光谱能量分布数据样本
本文从[30, 32, 35-39]中搜集了3C 279的29个态的光谱能量分布数据作为样本,观测的光谱能量分布数据是从射电波段到γ射线波段。文[40-41]指出,射电波段数据的流量产生于外喷流,在1012Hz时产生同步自吸收。然而,本文主要研究内喷流的多波段光谱能量分布拟合,因此不考虑射电波段的数据,但是拟合时对这部分数据也进行了限制,具体表现为:如果低频段有数据,那么拟合线在自吸收前的延长线不能高于数据形成的包络线。我们把观测时间在一周内的数据称为同时性数据,在两个月内的称为准同时性数据[42]。样本中有28个态的数据是同时/准同时性观测的光谱能量分布数据,一个态的时间为MJD 55300~55400,不是同时/准同时性数据,但我们把它作为平均态包含在样本中。样本及模型参数见表1。表1中每列的详细信息如下:第1列为样本观测时间;第2列为辐射区半径;第3列为磁场;第4列为多普勒因子;第5列为辐射区到黑洞的距离;第6列为电子能谱分布的归一化因子;第7列为电子的最小洛伦兹因子;第8列为电子的最大洛伦兹因子;第9列为电子能谱分布拐点的洛伦兹因子;第10列为同步峰左侧光薄段的谱指数;第11列为同步峰右侧光薄段的谱指数;第12列为卡方。
2 模型及拟合结果
2.1 模 型
本文统一使用单区轻子模型拟合3C 279的全部29个态的观测数据。本模型中假设辐射区域为半径R的球形,球形区域内充满均匀分布的电子,并以速度βc沿喷流方向运动。喷流方向与我们观测的视向夹角为θ,球形区域的洛伦兹因子为Г=(1-β2)-1/2。由于多普勒效应,观测到的辐射增亮,辐射区与中心黑洞的距离记为r。相对论电子与辐射区内部的磁场作用产生同步辐射,和同步辐射产生的软光子以及吸积盘、宽线区和尘埃环提供的软光子碰撞,产生逆康普顿散射。电子能量分布以拐折幂律谱的形式表示为[43]
N(γ)=N0γ-p1(γmin<γ<γb) ,
(1)
其中,N0为归一化系数;γmin和γmax为电子洛伦兹因子γ的最小值和最大值;γb为电子在拐点处洛伦兹因子;p1和p2分别为同步峰左侧和右侧光薄段的谱指数。得到稳态电子能谱分布后,我们使用公共PYTHON软件包NAIMA计算来自喷流的同步加速辐射、同步自康普顿(Synchrotron Self-Compton, SSC)辐射和外康普顿辐射[44]。
目前,单区模型依然应用广泛[39,45]。使用单区均匀轻子模型对耀变体的光变态光谱能量分布进行拟合,一方面可以得到各态内在物理参数包括辐射区所在位置的磁场、描述运动的多普勒因子和描述发出辐射的电子集的电子能谱分布特性参数等[22],而且在较大样本条件下使用同一个模型进行拟合后,可以对物理性质进行统计分析,从而对比得到不同态下源的物理特性;另一方面还可以利用拟合结果对前述三种可能的模型进行检验。
2.2 拟合结果
我们拟合使用的样本及模型参数见表1,光谱能量分布见图1~图4。拟合结果表明,拐折幂律谱电子能谱分布的稳态单区均匀轻子模型能够较理想地拟合29个包含光学、X射线和γ射线波段在内的光谱能量分布观测数据。
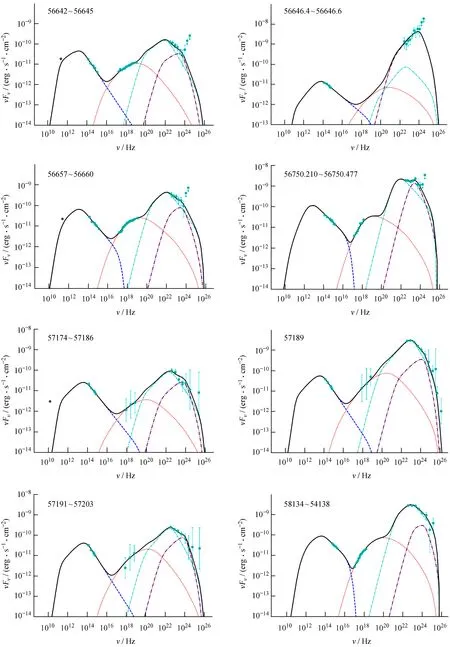
图2 单区均匀轻子模型拟合观测的3C 279的光谱能量分布图(9~16)Fig.2 The one-zone homogeneous lepton model is fitted to the SED data figure (9-16) observed by 3C 279

图3 单区均匀轻子模型拟合观测的3C 279的光谱能量分布图(17~24)Fig.3 The one-zone homogeneous lepton model is fitted to the SED data figure (17-24) observed by 3C 279
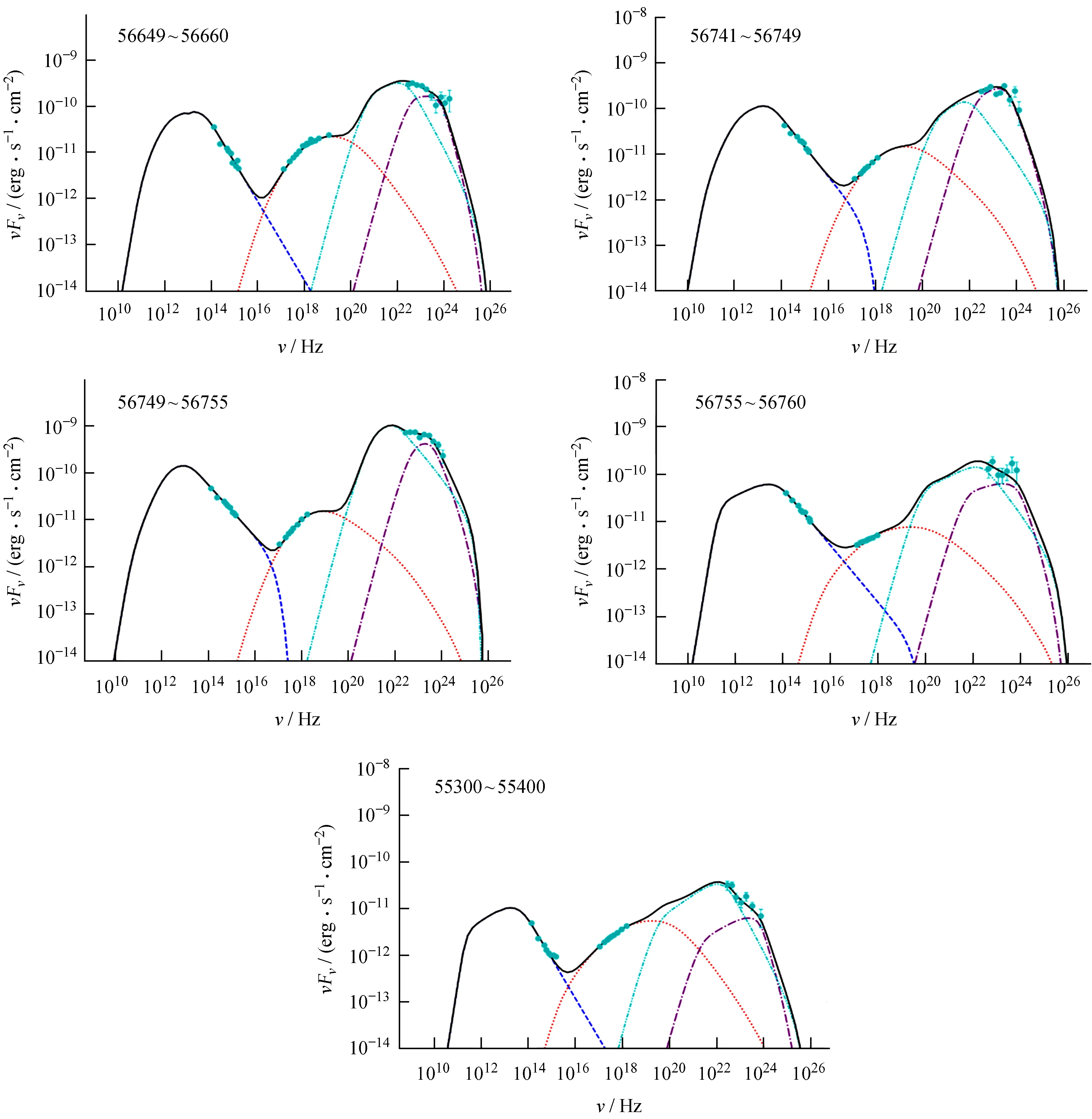
图4 单区均匀轻子模型拟合观测的3C 279的光谱能量分布图(25~29)Fig.4 The one-zone homogeneous lepton model is fitted to the SED data figure (25-29) observed by 3C 279
3 结果与讨论
3.1 拟合结果的物理性质和关系
在我们的拟合结果中,辐射区半径R的范围为1.3×1016~2.2×1017cm,与文[42]的结果一致。磁感应强度B的范围为0.103~0.51 G,与文[46]的结果一致。多普勒因子δ的范围为14~38.44,与文[46]的结果一致。
由于激波和磁重联机制产生的电子能谱分布各有特点:在电子能谱分布形如ne(γ)∝γ-p时,一般相对论性平行激波产生的电子能谱分布谱指数在p~2.2附近[47-50]。如果是相对论性的斜激波,也可能产生谱形较硬的电子能谱分布,p1[51]。而磁重联可以产生最硬到p~1的电子能谱[12]。于是我们可以通过电子能谱分布的谱指数对不同模型进行检验,并判断最可能的主导加速机制[52]。拟合得到电子能谱分布中能谱指数p1范围为1.7~2.7。如果在内激波的框架下解释3C 279的辐射,从p1的范围可以发现,相对论性平行激波(p~2.2)并不能完全解释我们的拟合结果,还需要相对论性斜激波才能够解释。另一方面,由于磁重联也能产生相同范围的电子能谱指数,所以它也是一个可能的解释。
同步峰的峰值频率和峰值光度的范围(峰值频率对数的均值为13.34,标准差为0.27;峰值光度的均值为46.66,标准差为0.28)比外康普顿峰的(峰值频率对数的均值为22.48,标准差为0.53;峰值光度的均值为47.69,标准差为0.60)小,这意味着无论是从频率还是光度对比,同步辐射的光变幅度都明显比外康普顿辐射的低,而且这个特性还导致一个相关性的产生。

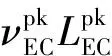
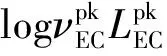

3.2 同步峰的峰值频率和峰值光度的相关性
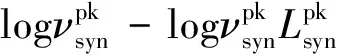

3.3 喷流的物理性质及辐射区位置
喷流功率对于我们了解喷流的产生和组成至关重要,我们可以通过光谱能量分布拟合参数估算喷流功率。通常假设喷流功率是由相对论电子、冷质子、磁场和辐射携带[41]:
Pjet=πR2Γ2c(Ue+Up+UB+Ur) ,
(2)
其中,Ue为相对论电子能量密度;Up为冷质子能量密度;UB为磁场能量密度;Ur为辐射能量密度,其计算公式为
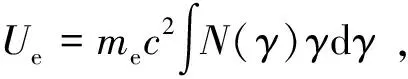
(3)
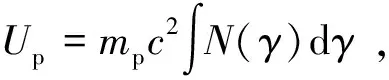
(4)
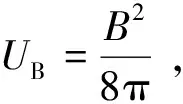
(5)
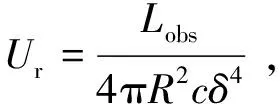
(6)
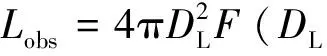

文[38]分析了3C 279在MJD 58129~58152时段的三个态,得到在两种γ射线辐射模型下,Ue和UB接近均分以及2018年1月的γ射线耀发外康普顿过程中的软光子是由尘埃环提供。文[39]分析了3C 279在MJD 57174~57203时段的三个态,得到在低态时粒子的能量密度和磁场能量密度接近均分,在耀发时这两者远离均分,表明喷流以粒子或物质主导的结论,并且指明造成耀发的可能原因是辐射区电子密度增加和耀发时辐射区小于低态的辐射区。参数Ue/UB的比值基本上远离1,所以两者之间均分的趋势不明显。同时从参数Ue/UB可以得到比值大于1的占86%,小于1的占14%,本文的研究表明3C 279中的喷流多数以粒子为主导,这与文[41, 60-61]的研究结果一致。
根据表2中的样本参数计算的每种成分所携带能量占总能量的比值,结果见表3。通过表3我们发现PB 表3 各成分(平均值)携带能量的比值 同时,我们根据文[60]中xBLR=0.1(Ld/1046erg-s)1/2pc和xDT=2.5(Ld/1046erg-s)1/2pc两个公式可以计算宽线区和尘埃环的特征位置,分别为xBLR=0.078pc和xDT=1.940pc。由表1可知,在我们的模型中γ射线耗散区位于0.1~1.8 pc的范围内,这意味着它们位于宽线区之外,尘埃环之内。从我们拟合结果中MJD 54827~54877,MJD 56646.4~56646.6和MJD 56741~56749时段的数据可以直观地看出,外康普顿过程的软光子以宽线区为主导,而其余26个态的外康普顿过程中的软光子以尘埃环为主导。因此,我们发现γ射线的辐射区一般位于宽线区之外,并且平谱射电类星体3C 279的外康普顿过程的软光子受尘埃环的影响较大。本文的结果与文[64-67]的研究成果一致,由于本文样本中同时/准同时性数据的辐射区位置相对分散,因此本文的结果更倾向于耗散区在宽线区之外。 本文基于稳态单区均匀轻子模型对29个态的同时/准同时性光谱能量分布数据的拟合,研究了平谱射电类星体3C 279的物理特性。主要结论如下: (1)我们通过拟合参数中电子谱指数的范围与前人理论中的范围对比发现,本文的结果支持光变的激波解释(但需要斜激波)或磁重联解释。 (3)同步峰的峰值频率和峰值光度之间的相关性一直用于反耀变体序列的研究。在本文的样本参数中发现两者之间不存在显著的正相关关系,这暗示了反耀变体序列不一定对所有的耀变体成立。 (4)在本文拟合参数中Ue/UB的比值基本上远离1,所以两者之间均分的趋势不明显。同时参数Ue/UB的比值大于1的占86%,表明3C 279中的喷流多数以粒子为主导。我们发现PB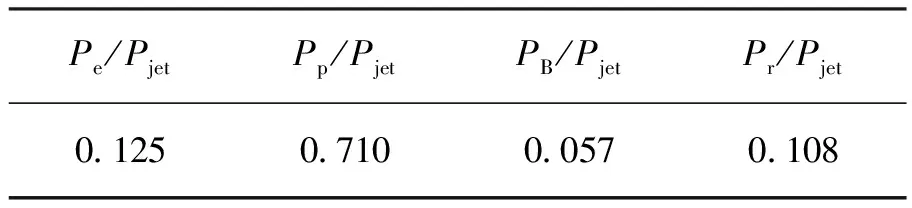
4 结 论