煤矿井下局部通风机需风量的预测

闫向彤，杨 琦

(西安科技大学 机械工程学院，陕西 西安 710054)

通风系统被认为是矿井的“血液循环系统”，是保障矿井安全和生产的重要基石。若系统出现故障往往导致风流紊乱、用风地点风量不足等安全隐患[1]。而局部通风机作为井下通风系统的核心动力，用风筒将新鲜风流送入掘进工作面，使得井下空气流通，有效降低事故率。然而由于煤矿井下通风机长期以恒定速度运行，造成了大量的电能浪费[2，3]。因此有必要根据井下瓦斯浓度、煤尘、温度、湿度等环境因素，利用改进的GA优化神经网络对井下局部通风机下一刻需风量进行预测研究，从而达到调整风速、节约能源、保障井下安全生产的目的。近年来人们对GA优化神经网络提出了很多改进，如文献[4]通过模拟退火算法全局搜索能力优化神经网络的连接权值与阈值，克服神经网络的缺陷，提高结果的准确性；文献[5]在遗传算法中引入禁忌搜索算子改进传统遗传算法的变异操作；文献[6]对遗传算法中变异算子进行了改进与优化，避免算法落入局部最优；文献[7]结合遗传算法能够改变局部搜素能力的特点，自适应地调整遗传算子的交叉和变异概率；文献[8]利用遗传算法采用随机竞争与最佳保留相结合的选择策略，使得计算效率提高。

本文根据矿井局部通风机的风量需求情况，建立了局部通风机需风量预测模型，提出了一种改进的遗传算法优化Elman神经网络，在选择算子的操作上进行改进，通过适应度由大到小降序排列后将前3个最优个体遗传至下一代，保证种群的最优策略；接着对剩余个体按照比例进行选择，将较优的个体组合形成新的种群，保存了种群的多样性；通过改进后的遗传算法在寻找最优的权值和阈值时，效率和精确度都得到提升。最后，运用改进的遗传算法优化的Elman神经网络对局部通风机需风量进行预测，从而实现风速调整，节省电能。

1 局部通风机需风量预测模型

矿井局部通风机提供的新鲜风量需求与井下环境有关，其中影响程度较深的是瓦斯浓度、温度、湿度及煤尘等因素。因此，本文将瓦斯浓度、温度、湿度与煤尘这四个环境参数作为Elman神经网络的输入变量，将局部通风机下一时刻需风量作为输出变量，建立的需风量预测模型如图1所示。利用改进的遗传算法去优化Elman神经网络，得到最优的权值和阈值，通过神经网络的训练，实现局部通风机需风量的预测与风速的调整。

图1 需风量预测模型

2 Elman神经网络

Elman神经网络作为一种动态递归网络[9]，是一种极具潜力的预测方法。它与前馈BP神经网络的不同点在于隐含层的结构中加入了一个连接层，使得它既有前馈连接，又有反馈连接，同时使Elman网络具有记忆能力，有效的克服了BP神经网络不具备动态特性的缺点。Elman神经网络一般分为四层：输入层、隐含层和输出层以及连接层，其输入层、隐含层和输出层的功能类似于前馈式BP神经网络，输入层单元用作信号传输的作用，隐含层单元利用线性或非线性函数对不同数据进行划分，输出层单元用作线性加权。而对于Elman神经网络增加的连接层用作延时与存储，使其对历史状态数据具有敏感性，增加了Elman神经网络对动态信息的处理能力[10-13]，这就使得整个Elman神经网络具有对时间序列进行预测的功能。

Elman神经网络的非线性状态空间表达式[14]：

y(t)=g(w3x(t))

x(t)=f(w1xc(t))+w2(u(t-1))

xc(t)=x(t-1)

(1)

式中，y(t)为t时刻m维输出层输出向量；x(t)为t时刻n隐含层节点向量；xc(t)为t时刻n维反馈状态向量；u为t时刻r维输入向量；w1、w2、w3分别表示连接层到隐含层、输入层到隐含层、隐含层到输出层的连接权值矩阵；g(.)为输出神经元的传递函数，是隐含层输出的线性组合；f(.)为隐含层神经元的传递函数[14]。

Elman神经网络判断算法是否结束的误差函数采用平方和函数。表达式为[15]：

(2)

式中，ei(t)为期望输出；m为样本总数；i为第i个样本。

3 遗传算法的改进

3.1 编码和适应度函数选择

Elman神经网络的权值和阈值是[-1，1]区间的小数，文中采用实数编码，该编码方式精确度高，适合解决复杂的优化问题。合适的适应度函数使得算法具有更高的精确性和效率，故用实际值与预测值的绝对值求和取倒数作为适应度函数[15]，表达式如下：

(3)

式中，yi是实际值，ai为预测值，n为Elman神经网络输出节点个数。

3.2 遗传算法操作

3.2.1 改进选择算子

遗传算法的选择算子常采用适应度比例法和最优个体保存策略。适应度比例法又称为轮转法，它存在随机误差的问题，在选择的过程中有可能会将适应度高的淘汰，适应度低的将被选中，尤其在种群数目多的情况下容易发生此类问题；而最优个体保存策略是将种群中适应度最高的个体不参与交叉、变异的运算，而是将适应度低的个体直接替换，这样的选择算子操作可能会破坏种群多样性，造成局部收敛。

以上的两种选择策略会影响遗传算法的全局搜索性，因此在保证种群多样性的前提下，本文提出了一种新的选择算子操作方法，该方法可以选出种群中较优的个体。接下来用种群数为18并且标有适应度值和编号的个体对改进的选择算子操作方法进行图文对应的描述：

1)确定一个初始种群并计算个体适应度值。

537161221920273310111716251430181716151413121110987654321

2)将种群内的个体按照适应度值由大到小排序。

333027252120171614121110976531819312105421367111614181715

3)选取前3个适应度值大的直接遗传下一代，其余按大小排序的个体均等分为三份。

4)均等的三份按照1，0.8，0.6比例进行选择，依据为优者居多、劣者少选，做到保存最优个体的同时也要保证种群的多样性。

5)将步骤4)中选取的个体重新组合形成新种群。

6)步骤5)中的新种群因为比例选取会有所减少，所以将步骤3)中直接遗传的个体复制一份。

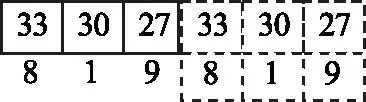
7)将复制的个体补充到步骤5)中形成新种群，以上一系列操作可以选取优良的个体，同时还可以保证种群的多样性。

最终的新种群与初始化种群相比，整体的适应度得到提高。该改进的选择算子操作对适应度值进行排序，在复制适应度优良的个体后，为保证种群的多样性对剩余个体进行按比例选取，此操作将大大提高算子的选优能力及网络的收敛速度。

3.2.2 交叉操作

根据改进的选择操作选中用于繁殖下一代的两个个体uk和ul，并随机选择两个个体相同的位置i，按交叉概率P进行随机信息交换，形成新个体。式中b为[0，1]之间的随机数。公式[16]如下：

(4)

3.2.3 变异操作

从种群中随机选取一个个体，对个体某些位进行一定概率的变异以产生更优秀个体，使该个体进入下一代的机会增加。通过对第i个个体第j个基因进行变异操作，表达式[16]如下：

f(g)=r2(1-g/Gmax)

(5)

式中，vmax和vmin分别为基因vij的上下界；r和r2均为[0，1]之间的随机数；g为当前迭代次数；Gmax为最大进化代数。

3.3 IGA-Elman神经网络算法实施步骤

改进的遗传算法通过优化Elman神经网络的初始权值和阈值使网络更好地预测输出，主要包括3个部分：创建Elman神经网络；改进遗传算法优化；网络预测结果[17]。步骤和流程如图2所示：①对数据进行归一化处理；②确定Elman神经网络结构，并初始化权值和阈值；③GA依次对Elman神经网络初始权值和阈值进行编码；④输入数据进行训练将输出误差作为各个个体的适应度值；⑤应用2.2小节提出的改进选择算子方法，选择出适应度高的个体并进行交叉和变异操作，计算出每代种群中的最大适应度值；⑥判断是否达到最大适应度值，若满足则进行解码获得最优权值和阈值，否则，进入步骤④；⑦算误差对网络的权值阈值进行更新，建立IGA-Elman网络模型。

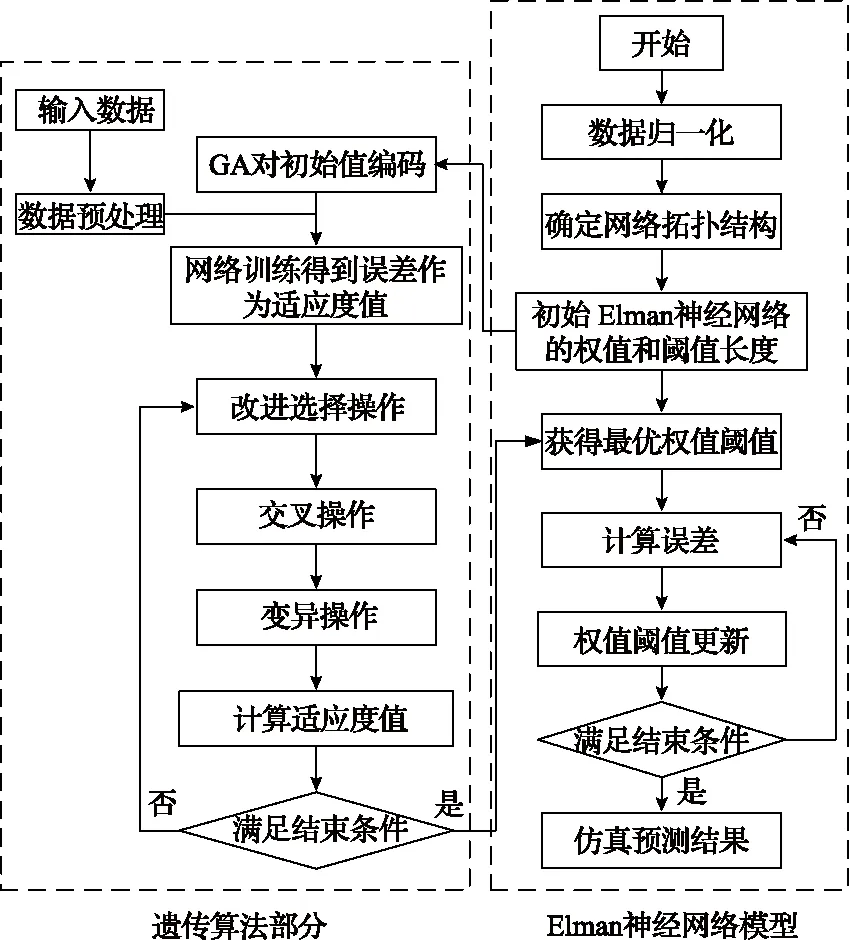
图2 改进的GA优化Elman神经网络算法流程

3.4 改进的遗传算法对Elman神经网络的影响

Elman神经网络是在BP神经网络的基础上通过添加一个连接层，构成了局部反馈，使得网络具有时变特性和动态记忆功能。但它同时也继承了前馈神经网络采用梯度下降算法对各层神经元间的权值和阈值进行修正，使得学习速度较慢，易陷入局部极小值等缺陷。对此本文对遗传算法的选择算子操作进行改进，在种群进化的过程中，利用复制优良个体及按比例选取较优个体的操作进行遗传，促使种群能向更好的进化方向发展，加快种群的进化速度，通过交叉与变异操作，提高新个体的质量。改进的遗传算法将加强局部搜索能力，使Elman神经网络较快地逼近最优权值和阈值，进而获得良好的收敛性能减小陷入局部极值的可能。

4 基于IGA-Elman神经网络算法的局部通风机需风量预测

对局部通风机需风量系统建立IGA-Elman神经网络预测模型，输入样本数据对网络进行训练得出最优的训练模型。为了更好地验证本文所提出的基于IGA-Elman神经网络算法的局部通风机需风量预测模型的预测效果，依据文献[18]中火铺煤矿的井下环境监测的数据，选取了瓦斯浓度、煤尘、温度、湿度、风速等对需风量具有较大影响的历史监测数据作为局部通风机需风量预测模型的训练。将样本数据分为两部分，一部分用于训练样本对IGA-Elman神经网络的训练，以达到允许的误差范围内；另一部分作为测试样本对训练好的预测模型进行预测分析，测试预测模型的效果，实现对下一时刻局部通风机需风量的预测。

经过参数设定，将样本数据输入至神经网络进行训练，仿真测试分别基于GA-Elman神经网络与IGA-Elman神经网络算法建立局部通风机需风量预测模型，对比两者预测模型最优个体适应度值曲线如图3所示。

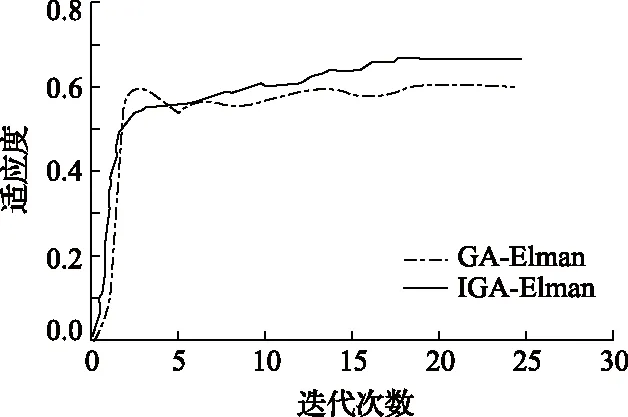
图3 GA-Elman与IGA-Elman网络个体适应度曲线

从图3中可以看出，IGA-Elman算法寻找最优的权值阈值能力要强于GA-Elman。在迭代的过程中，虽然GA-Elman网络能较快的收敛，但它出现了多次适应度下降的现象，使得每次迭代的过程中有最优个体被淘汰的可能，而IGA-Elman神经网络通过对选择算子的改进及最优个体保存的策略，使得整体的平均适应度得到提升且在迭代18次左右时适应度值趋于稳定，体现出较强的自适应性能。

IGA-Elman网络与GA-Elman网络训练的均方误差曲线如图4所示。从图4中可以看出，传统的GA-Elman神经网络的总体运行时间与均方误差都要高于改进的IGA-Elman网络运行时间与误差，主要是由于IGA-Elman神经网络改进了选择算子后计算量较之前相比减少引起的，使得遗传算法选优能力得到改善。

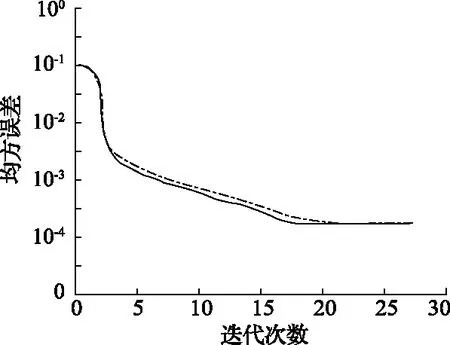
图4 GA-Elman与IGA-Elman网络均方误差曲线

经上述对神经网络模型的训练后得到最优模型，利用优化好的网络模型对局部通风机需风量进行预测，本文依据黄陵柠条塔煤矿测得实时风量及井下环境参数，将各个参数输入至前文优化的网络模型进行预测，预测结果与实际风量的误差见表1。

通过对表1的分析可以看出，由于传感器本身精度的误差与井下环境的特殊性等因素，造成IGA-Elman网络的预测值与实际测量值之间存在较小的误差，但改进的IGA-Elman网络对需风量的预测相对误差精度要高于传统GA-Elman网络，所以改进的遗传算法优化的Elman神经网络对局部通风机需风量的预测精度较高，效果更好。

表1 预测结果对比

5 结 语

本文提出了一种改进的遗传算法优化Elman神经网络的局部通风机需风量预测模型。对传统的遗传算法进行改进，通过对选择算子进行择优复制遗传下一代及按比例选择较优的个体相结合的操作，使改进的遗传算法提高了全局搜索能力，为Elman神经网络训练出最优的权值和阈值奠定了基础，进而更加准确的预测出局部通风机下一刻风量的需求，实现风速的调整。