致密气藏压裂水平井温度剖面影响因素分析
2021-10-26罗红文李海涛安树杰邹顺良
罗红文,李海涛,安树杰,辛 野,李 磊,邹顺良,李 颖,刘 畅
(1.西南石油大学油气藏地质及开发工程国家重点实验室,四川 成都 610500;2.中油奥博科技有限公司,四川 成都 610097;3.中海油能源发展股份有限公司,天津 300454;4.中国石油华北石油管理局有限公司,河北 廊坊 065000;5.中国石化江汉石油工程有限公司,湖北 武汉 430073)
0 引 言
近年来,分布式光纤温度测试(DTS)技术发展十分迅速,且越来越多地被应用于油气藏水平井井下动态监测中,DTS的显著优势在于可以对全水平井段的温度剖面进行实时监测,提供连续准确的温度剖面数据[1-3]。因此,不少学者也指出,根据DTS所测温度剖面不仅可以定性识别人工裂缝、判断流体类型、评价压裂改造效果等,其更重要的意义在于可以根据DTS数据定量解释压裂水平井产出剖面、裂缝流量贡献及裂缝参数等[4-5]。然而,要达到这一目的,首先必须实现压裂水平井温度剖面预测并找到影响压裂水平井温度剖面的主导因素。基于直井温度模型[4-6],国内外学者在水平井温度剖面预测方面做了许多研究,也取得了一定的成果。Yoshioka等[7]建立了最早的考虑焦耳-汤姆逊效应、热对流和热传导的水平井稳态温度模型,随后又考虑多相流的影响,建立了新的两相流水平井温度模型,并分析了不同流体流入时水平井温度剖面的变化情况[8-9]。Muradov等[10]建立了适用于单相产油或产水的水平井稳态温度模型,并根据温度剖面测试数据反演解释水平井产出剖面。Li等[11]建立了一套水驱油藏水平井温度动态模型,并进行了实例分析。Radespiel[12]提出了一个简化的一维井筒温度模型来计算水平井井筒中的温度变化。朱世琰[1]和蔡珺君等[13]也分别建立了油水两相水平井温度剖面预测模型,还讨论了不同因素对水平井温度剖面的影响规律。然而,关于压裂水平井温度剖面预测方面的研究相对较少,Yoshida等[14]建立了单相页岩气藏压裂水平井稳态温度预测模型,但模型仅适用于均质储层的情况。Cui等[15]基于三线性流假设,建立了考虑人工裂缝的页岩气藏压裂水平井半解析稳态温度模型,但模型中未考虑储层各向异性和井筒摩擦对温度剖面的影响。由此可见,目前压裂水平井温度剖面预测方面的研究仍存在着诸多不足,尤其是针对致密气藏压裂水平井温度剖面预测方面的研究鲜有涉及。因此,此次研究建立了一套致密气藏压裂水平井温度剖面预测模型,通过耦合求解,实现了不同裂缝参数情况下的致密气藏压裂水平井温度剖面预测;分析了压裂水平井温度剖面的分布特征,并分别采用正交实验分析法和定量实验分析法评价了温度剖面的影响因素和敏感性,确定了影响致密气藏压裂水平井温度剖面的主导因素,为致密气藏压裂水平井产出剖面、裂缝参数等定量解释奠定了理论基础。
1 致密气藏压裂水平井温度剖面预测模型
基于质量守恒、能量守恒原理,建立如图1(箭头为流体流动方向)所示箱型致密气藏压裂水平井温度剖面模型。为了准确预测致密气藏压裂水平井温度分布,在建立温度剖面预测模型时,考虑了包括焦耳-汤普逊效应、热对流、热传导、黏性耗散和热膨胀等微量热效应,以及井筒内摩擦生热对井筒温度剖面的影响,而且,还建立了独立的裂缝系统渗流模型和热学模型,并将其与井筒模型耦合求解。如图1所示,温度模型包括了储层、人工裂缝和井筒(固井分段压裂完井)3个部分,对各部分都分别建立了对应的渗流模型和热学模型用以表征各部分之间的流体交换和热量传递。
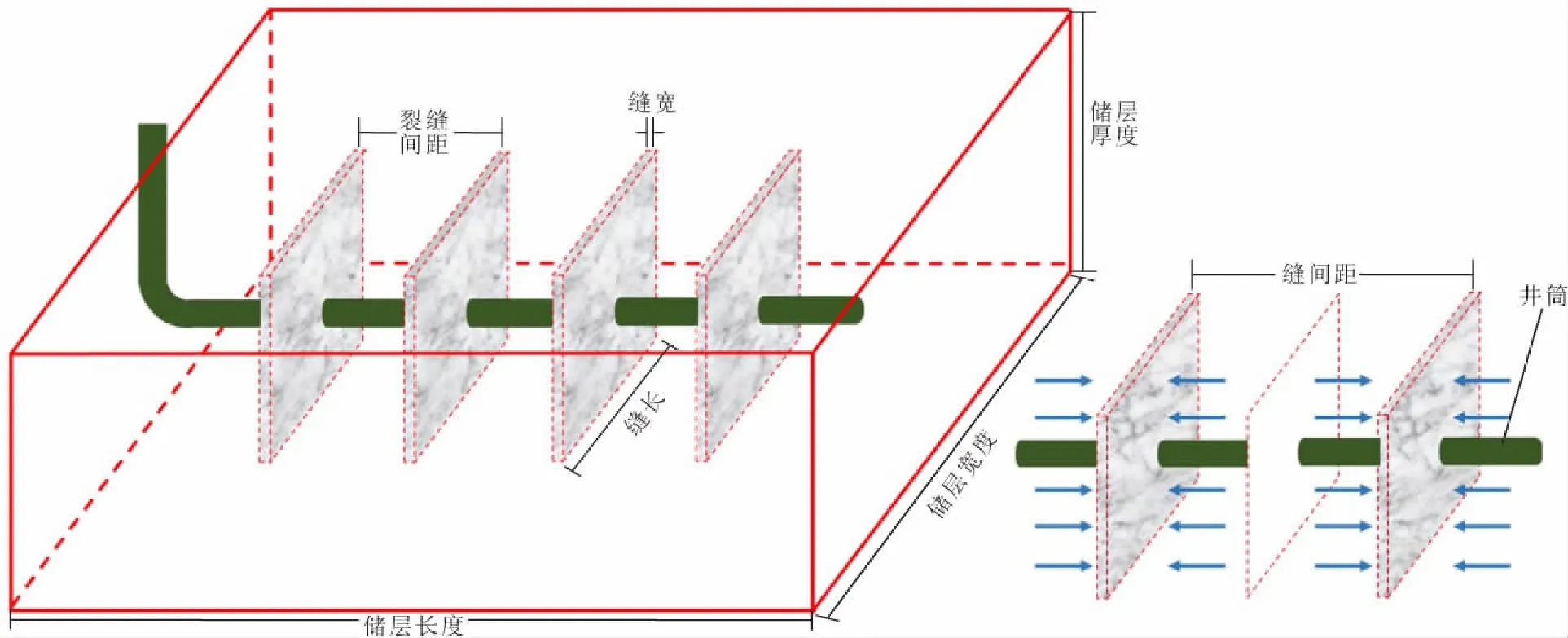
图1 箱型致密气藏压裂水平井模型示意图
1.1 储层模型
(1) 储层渗流模型。基于质量守恒原理,引入拟压力函数,建立储层渗流模型,计算储层中的压力分布。

(1)
式中:φ为储层孔隙度;μg为气体黏度,mPa·s;Cg为气体压缩系数,MPa-1;ψ为气相拟压力[16-17],MPa2/(mPa·s);t为生产时间,d;Kx、Ky、Kz分别为x、y、z方向的储层渗透率,mD。
(2) 储层热学模型。基于能量守恒方程[18],考虑了焦耳-汤普逊效应、热对流、热传导、黏性耗散和热膨胀等微量热效应对温度剖面的影响,建立储层热学微分方程:
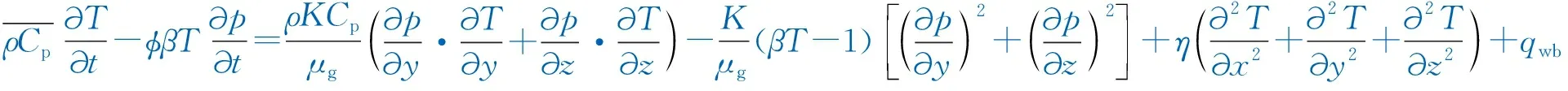
(2)
(3)
式中:Cp为流体或储层岩石比热容,J/(kg·K);ρ为流体或储层岩石密度,kg/m3;Cpg为流体比热容,J/(kg·K);Cps为储层岩石比热容,J/(kg·K);ρs为储层岩石密度,kg/m3;ρg为流体密度,kg/m3;β为热膨胀系数,1/K;K为储层渗透率,mD;T为储层温度,K;η为储层热导率,J/(m·s·K);p为储层压力,MPa;qwb为井筒和储层之间单位体积的热传导速率,J/(m3·s)。
1.2 人工裂缝模型
人工裂缝模型是基于储层模型建立的,由于人工裂缝宽度较小,可忽略流体在裂缝宽度方向的流动,而且,在人工裂缝内部,由于流体流动引起的热对流导致能量变化占据绝对主导地位,而由热传导引起的能量变化可以忽略。
(1) 人工裂缝渗流模型如下:
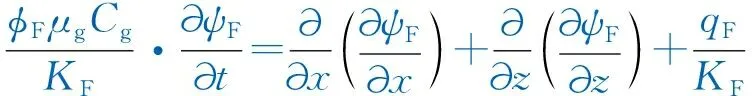
(4)
式中:qF为人工裂缝中的流体流速,m/s;KF为人工裂缝的渗透率,mD;ψF为人工裂缝中的气相拟压力,MPa2/(mPa·s);φF为人工裂缝的孔隙度。
(2) 人工裂缝热学模型如下:
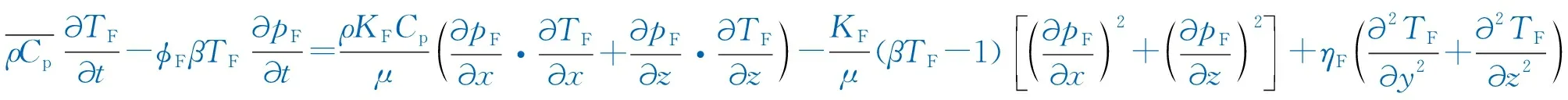
(5)
式中:ηF为人工裂缝的热导率,J/(m·s·K);TF为人工裂缝的温度,K;pF为人工裂缝中的压力,MPa。
1.3 井筒模型
基于质量守恒、动量守恒和能量守恒原理,建立了固井分段完井的水平井井筒流动模型和热学模型,分别计算压裂水平井井筒中的压力和温度分布。为提高模型精度,在井筒模型中还考虑了摩擦生热对井筒温度的影响,并与储层、裂缝模型耦合求解。
(1) 井筒流动模型:
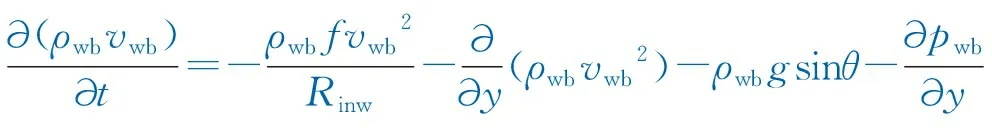
(6)
式中:Rinw为井筒内径,m;pwb为井筒中的压力,MPa;ρwb为井筒中的流体密度,kg/m3;f为井壁摩擦系数;vwb为井筒中的流体流速,m/s;θ为水平段井筒倾角,°;g为重力加速度,m/s2。
(2) 井筒热学模型:
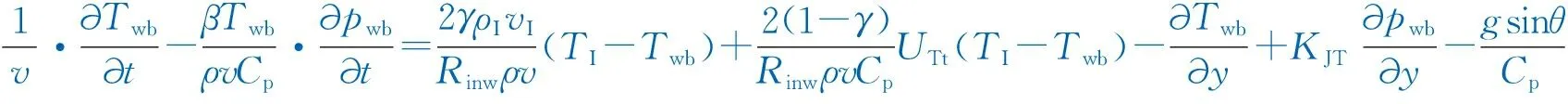
(7)
式中:TI为人工裂缝流入井筒的流体的温度,K;γ为井筒打开程度[19](井筒打开面积与井筒总面积之比);Twb为井筒中的温度,K;UTt为综合传热系数[2],J/(m2·s·K);KJT为焦耳-汤普逊系数[20],K/MPa;ρI为人工裂缝流入井筒的流体的密度,kg/m3;vI为人工裂缝流入井筒的流体流速,m/s。
1.4 储层、人工裂缝及井筒热学模型耦合及求解
由式(7)所示的井筒热学模型可知,要想获得压裂水平井温度剖面,关键在于求取人工裂缝流入井筒的流体温度。因此,需要将储层、人工裂缝及井筒热学模型通过热能源汇项进行耦合[14,21],当然,在耦合求解时,还需要考虑对应的边界条件和初始条件[22]。但考虑到固井分段压裂完井方式的特点,在固井段和井筒打开段(人工裂缝位置),热量传递的方式不同,因此,在固井段和井筒打开段分别进行热学模型耦合。
(1) 固井段热学模型耦合。在固井段,储层主要通过热传导向井筒中不断传热,即:
(8)
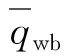
(2) 井筒打开段(人工裂缝位置)热学模型耦合。在井筒打开段,主要通过流体流入将热量携带至井筒中,则:

(9)
式中:r为径向半径,m。
式(9)右边第1项为热对流项,与井筒热学模型式(7)中的热对流项相对应。
从热力学模型耦合过程可以看出,储层、人工裂缝和井筒热学模型为相互耦合且非线性的。因此,需要通过迭代实现耦合温度模型求解,首先输入基础模型参数,通过气藏、裂缝渗流模型计算出储层和裂缝中压力分布,将获得的储层和裂缝压力分布代入井筒流动模型中计算井筒流量剖面和压力剖面;然后将计算所得的储层和裂缝中的压力分布分别代入气藏和裂缝热学模型,计算出储层和裂缝中的温度分布,并将获得的储层和裂缝中温度分布代入耦合温度模型计算出人工裂缝流入井筒的流体的温度剖面(TI),将TI代入井筒热学模型,即可计算出压裂水平井井筒中的温度剖面。
2 致密气藏压裂水平井温度剖面模拟预测
采用上述建立的耦合温度剖面预测模型,对致密气藏压裂水平井进行了温度剖面模拟,以分析致密气藏压裂水平井温度分布特征,为温度剖面影响因素分析奠定基础。模拟计算所需的基础参数如表1所示,各级裂缝参数如表2所示。
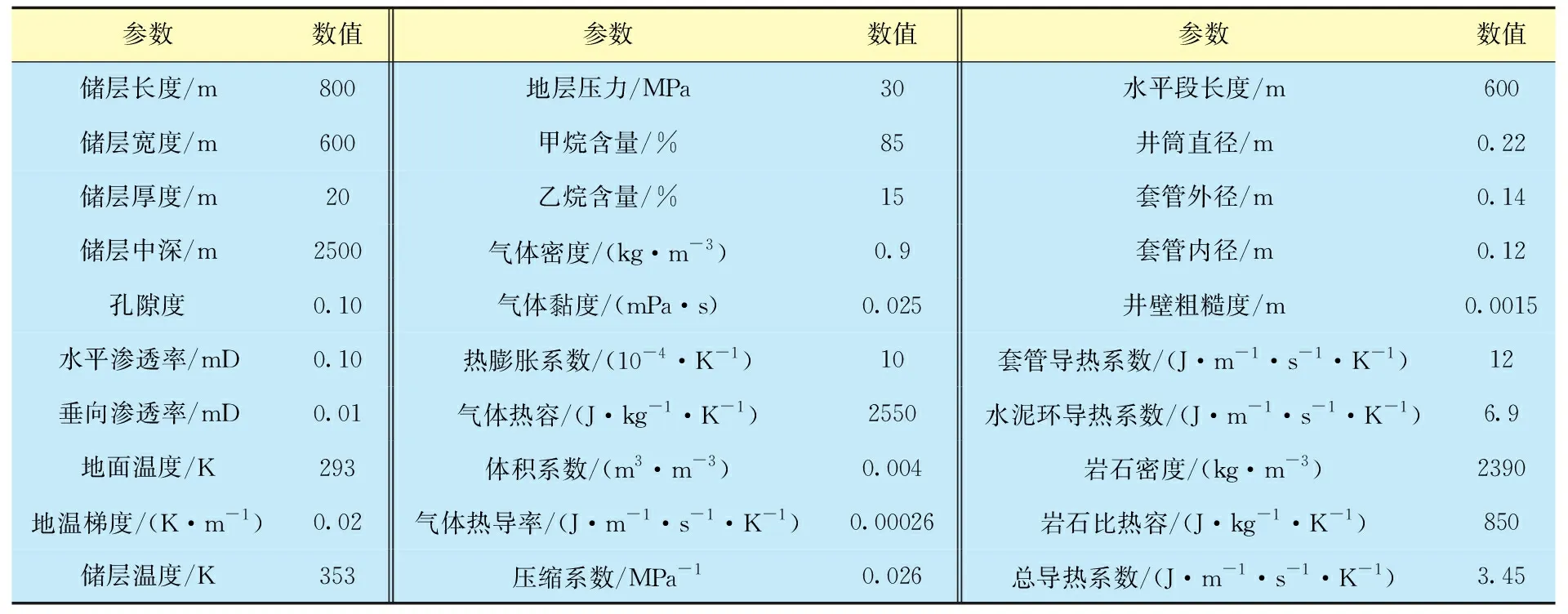
表1 压裂水平井基础参数

表2 压裂水平井各级裂缝参数
图2为裂缝附近区域的储层温度分布。由图2可知:在裂缝跟端位置存在明显的温度降,其原因为气体在裂缝位置处经射孔孔眼流入井筒,产生较大节流压降,使得气体从裂缝流入井筒时的焦耳-汤姆逊冷却效应急剧增强;此外,经单一裂缝流入的气体与井筒中已有气体在裂缝跟端位置发生混合,产生的混和温度降进一步增强裂缝跟端的冷却效应,两者共同作用使得裂缝跟端位置存在明显的温度降。因此,气藏压裂水平井生产时,由于流体从地层不断流入井筒,从储层外边界到井筒压力不断降低,压降引起的冷却效应逐渐累积,使得储层向裂缝温度逐渐降低,在裂缝跟端位置储层温度达到最低值(图3)。
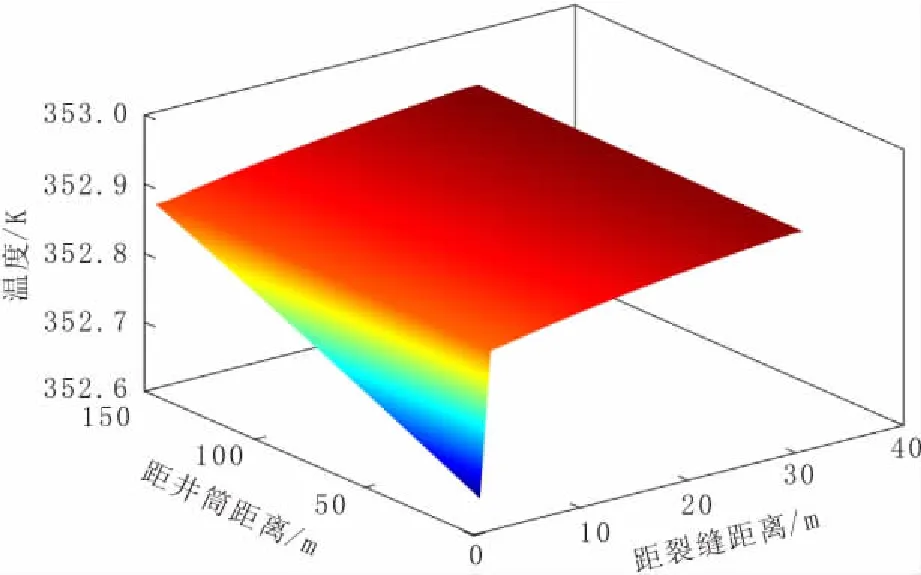
图2 裂缝附近区域储层温度分布

图3 压裂水平井储层温度分布
图4为压裂水平井井筒温度剖面。由图4可知:压裂水平井井筒温度剖面在裂缝处存在明显的温度降。这是由于气体经裂缝流入井筒时,在裂缝跟端产生的压降较大,焦耳-汤姆逊冷却效应使得流入井筒的气体温度降低,从而导致裂缝位置处存在温度降;而在固井段,由于无流体直接流入井筒,仅通过套管以热传导的方式,不断向井筒中传递热量,从而加热井筒中的流体,同时,井筒中还存在流体与井壁之间的摩擦生热效应,裂缝处的降温和固井段的加热效应共同作用使得压裂水平井井筒温度剖面呈现出不规则的“锯齿状”。从水平井趾端到跟端,裂缝处的降温和固井段的升温交替重复出现,任一“锯齿”(即“降温+升温循环”)都指示着一条有流量贡献的人工裂缝,而且,“锯齿”越长,对应的裂缝半长越大,裂缝流量贡献越大。只有对水平井产量有贡献的有效支撑裂缝,才会呈现出对应的温度响应。因此,根据这一温度剖面特征,并结合实测DTS温度剖面可对有效人工裂缝进行直观识别和诊断。这对于现场压裂水平井压裂效果评价以及指导重复压裂等具有实际意义。

图4 压裂水平井井筒温度剖面
3 致密气藏压裂水平井温度剖面影响因素分析
分别采用正交实验分析法和定量实验分析法,对影响压裂水平井温度剖面的单因素进行了敏感性分析,并对单因素对温度剖面的影响程度进行排序,模拟计算所需的基础参数仍如表1所示。
3.1 正交实验分析
正交实验分析的最终目的是评价各因素对井筒温度剖面的影响程度,选取了单井日产气量(Qg)、储层渗透率(K)、储层总导热系数(η)、裂缝半长(xf)、裂缝导流能力(FCD)、井筒直径(D)、水平段井筒倾角(θ)这7个对压裂水平井筒温度剖面影响相对较大的参数建立正交分析表,正交实验分析因素及其取值水平如表3所示。在正交实验分析过程中,以原始地层温度与各裂缝位置处井筒温度之差的平均值作为实验指标。该实验指标基本反映了随不同因素变化时,地层流体从储层边界流入井筒时的整体温度降低程度,并通过极差法对实验结果进行分析。

表3 正交实验分析因素及取值水平
根据正交实验设计选取的单因素和各因素水平设计,选用L18(37)的标准正交表进行正交实验分析,正交实验方案如表4所示(表中1、2、3分别和表3中水平1、水平2、水平3对应)。极差分析结果(表5)表明,各单因素对压裂水平井温度剖面的影响程度从大到小依次为:裂缝半长、单井日产气量、储层渗透率、井筒直径、裂缝导流能力、水平段井筒倾角、储层总导热系数。
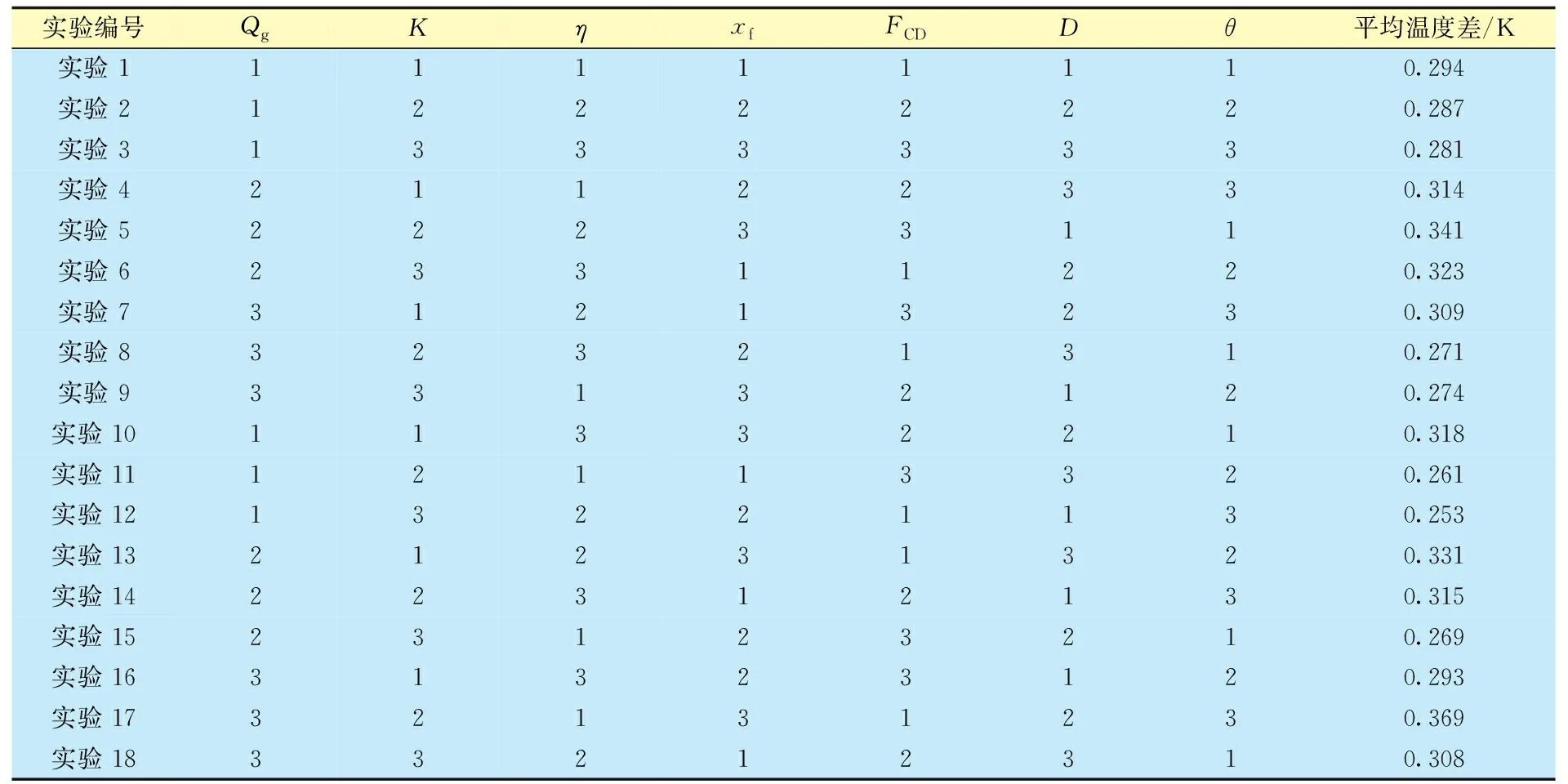
表4 正交实验方案

表5 正交实验结果
3.2 定量实验分析
采用定量实验方法评价压裂水平井温度剖面变化对各因素的敏感性,之所以称之为定量,即是在各单一因素指定变化量情况下,通过计算井筒温度剖面的改变量,对比分析井筒温度剖面变化程度,以此来评价井筒温度剖面对各因素的敏感性。
共设计了1个参考实验和7个对比实验,以参考实验作为基准,每一次实验仅改变一个单因素的取值,均在参考实验的单因素取值的基础上增加10%,其余单因素取值则保持不变,仍与参考实验保持一致。定量实验分析时,以压裂水平井在中间裂缝位置处的井筒温度的变化量作为实验指标,定量实验方案设计及实验结果如表6所示。
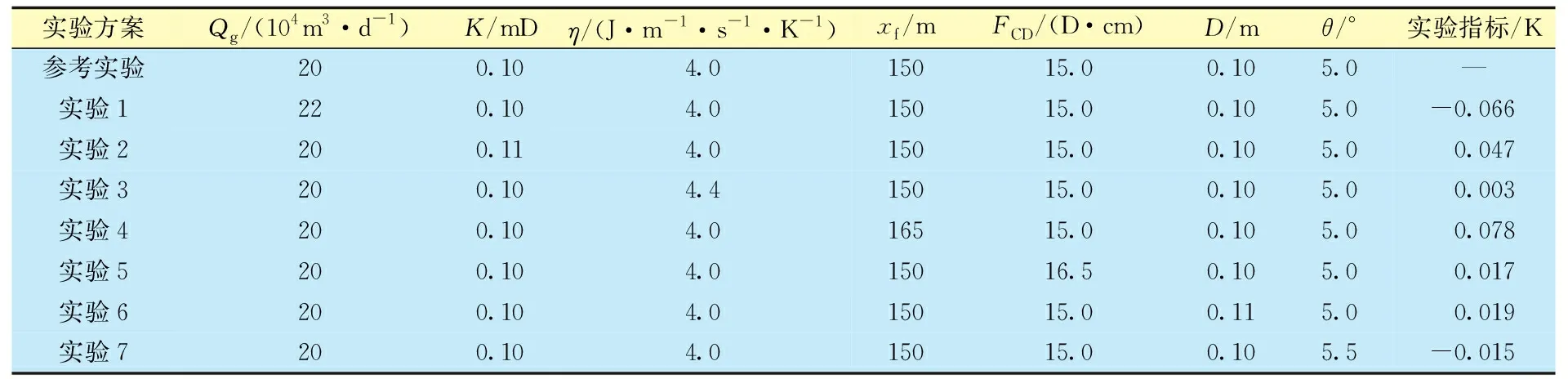
表6 定量实验方案及实验结果
定量实验分析结果表明:裂缝半长、单井日产气量和储层渗透率变化引起的井筒温度变化量明显高于其他几个因素(表6)。各单因素定量变化引起的井筒温度变化量绝对值从大到小排序为:裂缝半长、单井日产气量、储层渗透率、井筒直径、裂缝导流能力、水平段井筒倾角、储层总导热系数,与正交实验分析结果相一致。而且,从表6所示的井筒温度(实验指标)随各因素定量增加时的改变量还可以看出,储层渗透率、储层总导热系数、裂缝半长、导流能力和井筒直径与井筒温度剖面的变化呈正相关;单井日产气量和水平段井筒倾角与井筒温度剖面变化呈负相关。
根据正交实验和定量实验分析结果可知,影响致密气藏压裂水平井温度剖面的主导因素是裂缝半长、单井日产气量和储层渗透率。因此,当储层渗透率分布已知时(或均质储层),结合温度剖面上“锯齿”的长度,可以对各级裂缝的流量贡献进行初步估算。更进一步地,可分别以裂缝半长或地层渗透率作为反演目标参数,并以文中建立的温度剖面预测模型作为DTS数据反演时的正演模型,然后根据合理的数学算法(如L-M算法[21,24-25]、MCMC算法[1,26]、SA算法[27]等)建立反演模型,对致密气藏压裂水平井实测DTS数据进行反演,就可定量解释出致密气藏压裂水平井产出剖面、裂缝流量贡献及具体的裂缝参数。
4 结 论
(1) 建立了考虑诸多微量效应和井筒摩擦生热的致密气藏压裂水平井温度预测模型,并通过耦合求解,实现了不同裂缝参数情况下的致密气藏压裂水平井温度剖面预测,该温度模型还可用作致密气藏压裂水平井DTS数据反演时的正演模型。
(2) 致密气藏压裂水平井生产时,储层向裂缝温度逐渐降低,在裂缝跟端位置储层温度达到最低值;井筒温度剖面呈现出不规则的“锯齿状”,任一“锯齿”都指示着一条有流量贡献的人工裂缝,“锯齿”越长,对应的裂缝半长越大,裂缝流量贡献越大。因此,可以根据实测DTS温度剖面对有效人工裂缝进行识别和诊断。
(3) 正交实验和定量实验分析表明各单因素对致密气藏压裂水平井温度剖面的影响程度由大至小依次为:裂缝半长、单井日产气量、储层渗透率、井筒直径、裂缝导流能力、水平段井筒倾角、储层总导热系数;其中,储层渗透率、储层总导热系数、裂缝半长、导流能力和井筒直径与井筒温度剖面的变化成呈相关,单井日产气量和水平段井筒倾角与井筒温度剖面变化呈负相关。
(4) 影响致密气藏压裂水平井温度剖面的主导因素是裂缝半长、单井日产气量和储层渗透率,在进行致密气藏压裂水平井实测DTS数据反演时,可分别以裂缝半长或地层渗透率作为反演目标参数。
