无模型自适应控制在仿真化工厂的应用
2021-10-26曾凯钱俊磊徐越刘博安江伟
曾凯,钱俊磊,徐越,刘博, 安江伟
(1. 华北理工大学 电气工程学院,河北 唐山 063210;2. 广西科技大学 电气与信息工程学院,广西 柳州 545616;3. 星恒检测有限公司,河北 唐山 0630204;4.唐山阿诺达自动化有限公司,河北 唐山 063020)
评价工业控制品质的指标是快速性、稳定性和准确性。基于反馈控制系统偏差的PID控制器在实际的工业控制领域中广泛应用。随着生产过程的复杂化发展,非线性、时变、大滞后、多耦合等环节导致被控系统很难精准建模,在应对这种没有准确被控对象模型的被控生产过程的情况时,PID控制器的控制能力越来越有限。比如在复杂化工工业领域内,当反应釜涉及的反应过程比较复杂、被控参数比较多的情况下,简单的PID控制器很难得到快速、准确的控制结果。
为了解决上述复杂系统的控制问题,除了系统建模、参数辨识等手段,无模型在线数据驱动控制的方法得到了很好的控制效果[1]。基于在线数据驱动的无模型自适应法,动态化达到无模型自适应控制(Model Free Adaptive Control,MFAC),即系统的每一次输入输出数据更新,都作为历史数据的参考对被控系统模型的预测进行更新调整,是非静态化的模型[2]。根据推导出的MFAC的系统结构,可知其线性模型结构参数少,在应用过程中仅需求解步长序列和伪偏导数即可,大大简化求解过程,最终得到的闭环控制系统,动态性能指标较PID控制效果在快速性、准确性和稳定性等方面都更有优势。
1无模型自适应理论
1.1 泛模型定义
一般的输入输出非线性离散时间系统模型如式(1)所示:
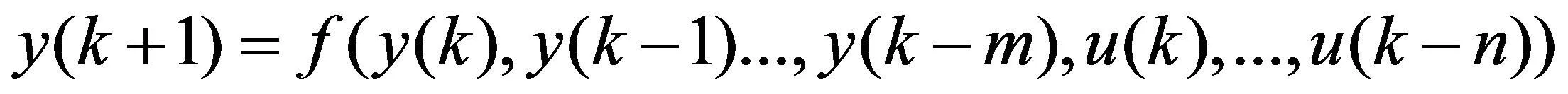
(1)
其中,y(k)表示被控系统的输出,u(k)表示被控系统的输入,m和n分别表示系统输出与输入的阶数,f(…)表示待计算非线性函数[3]。
对于非线性离散系统(1)来说,在Δu≠0和任意时刻k,一定会存在一个量φ(k),使得式(2)成立:
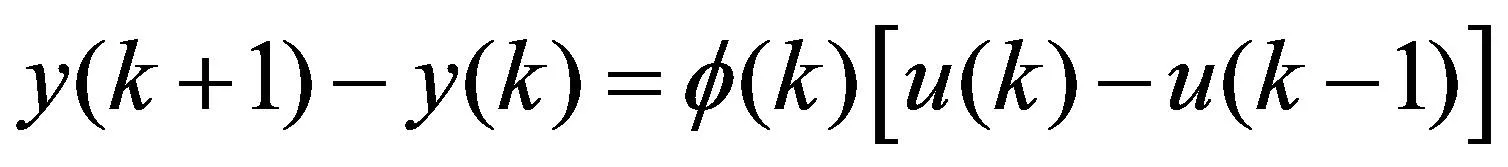
(2)
经过整理可得式(3):

(3)
式(3)叫做非线性系统的泛模型,φ(k)定义为伪偏导数,有界且时变。
1.2 MFAC控制律
在对泛模型参数进行求解时,由于非线性系统的性质,需要限制控制输入的变化量,控制输入变化过大时,u(k)与φ(k)的关系不能忽略,引入新的控制输入准则函数如式(4)所示[4]:
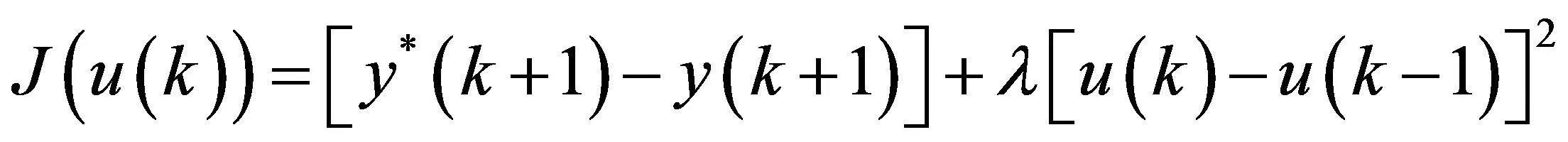
(4)
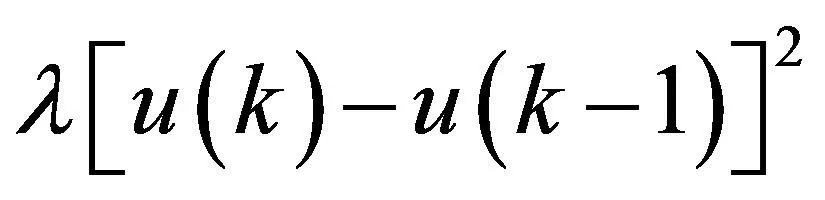

(5)
1.3 计算伪偏导数
根据最小二乘法,卡尔曼滤波法估计伪偏导数具有一定的局限性,这些方法的估计值变化过快,所以提出新的参数估计准则标准,得到伪偏导数控制律如式(6)[5]:
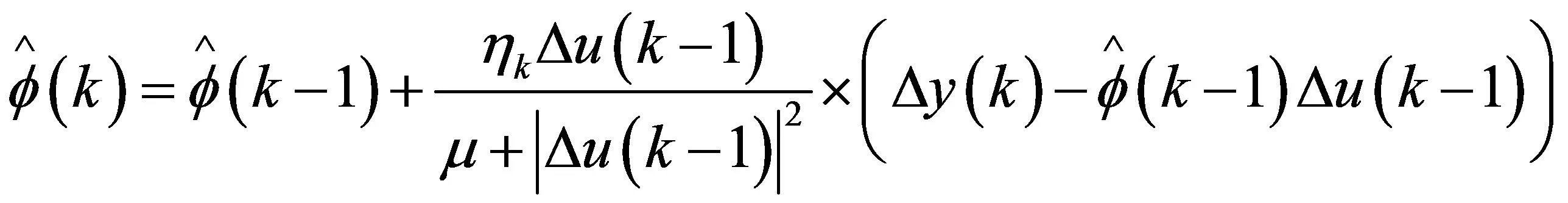
(6)
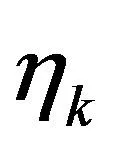
由式(3)至(6)可见,MFAC算法对受控对象同时进行建模和参数辨识,估计输入输出数据后,获得一个伪偏导数,然后对被控系统进行反馈控制后得到新的输入输出数据,在基于以往的输入输出数据重新进行参数辨识,得到新的伪偏导数,如此迭代下去,不断地缩小系统偏差,直到满足控制要求,算法的结构如图1所示。

图1 MFAC算法结构图
2仿真研究与分析
2.1 SISO连续时间系统的仿真

图2 SISO连续系统的MFAC和PID仿真控制曲线
根据式(3)至式(6),调整无模型自适应的参数,设定伪偏导数φ(k)为3,μ为1.2,λ为0.9,ηk为1,仿真结果如图2中黑色虚线所示; PID控制器,δ整定参数后得到最佳参数 为1.4,Tl为0.2,TD为0.4,仿真控制曲线如图2中橙色实线所示。
从图2可知,经PID调节的控制系统超调量比较大,曲线放大后可见系统偏差一直存在,稳定性一般;而经MFAC调节的被控系统超调量小、偏差小,系统的稳定性更好,使得受控系统应对各种变化具有超常的自适应性以及鲁棒性,具有很好的综合控制效果。
2.2 SISO离散非线性系统的仿真
图2仿真曲线表明MFAC系统在连续系统控制中的优越性,在MFAC仿真中,式(7)作为被控系统数学模型不参与运算,只使用模型的输入输出的数据。
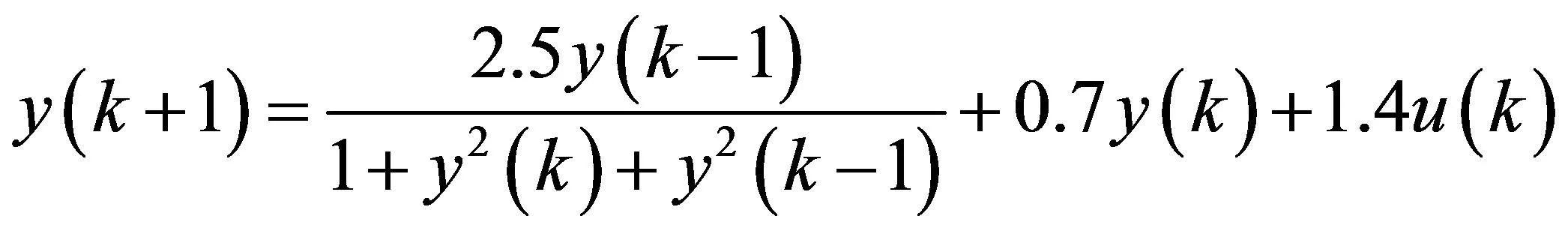
(7)
调节MFAC控制器的ηk和λ,得到最佳的参数λ为0.01,ηk为0.5,令输入的信号源为方波矩阵,运行MATLAB中的脚本文件,得到图3所示仿真曲线;同样根据经验整定,得到PID的最佳参数为:δ为0.2,Tl为0.5,得到图4的仿真结果。

图3 离散系统MFAC的跟踪结果 图4 离散系统PID调节结果
对比图3和图4可以发现,利用MFAC进行控制的仿真结果动态性能比PID调节的速度更快,追踪性能更好,超调量和偏差更小,远远优于PID调节,并且用MFAC控制参数较少,逻辑清晰。
2.3 MFAC-PID控制系统的仿真


图5 串级系统MFAC和PID对比仿真模型
经过参数整定,得到的MFAC-PID串级控制器ηk最佳为0.95,λ为1.75,PID串级的最佳参数δ为1.3,Tl为1.2,TD为0.4,仿真结果曲线如图6所示,黑色虚线为MFAC-PID串级控制,橙色实线为双PID串级控制。根据仿真结果可见,对于有较大滞后的被控系统,传统的双PID串级系统偏差一直存在,并不能得到有效的控制,很难维持高精度稳定状态。然而MFAC-PID控制系统的整体动态性能指标较好,较双PID串级系统有明显优势。

图6 串级系统MFAC和PID对比仿真结果图
3基于PCS7的MFAC在虚拟化工厂的应用
西门子SIMATIC PCS7是分布式控制系统(Distributed Control System,DCS)的一个应用实例,为工业控制领域提供大范围组态、软件、硬件配置和诊断工具,满足化工、制药、冶金等行业的应用需求[9]。
如图7的虚拟化工厂工艺流程基于SMPT1000的流程工业系统仿真平台进行控制,控制系统采用PCS7和西门子S7-400系列控制器,算法模块开发采用结构化控制语言(Structured Control Language,SCL)。
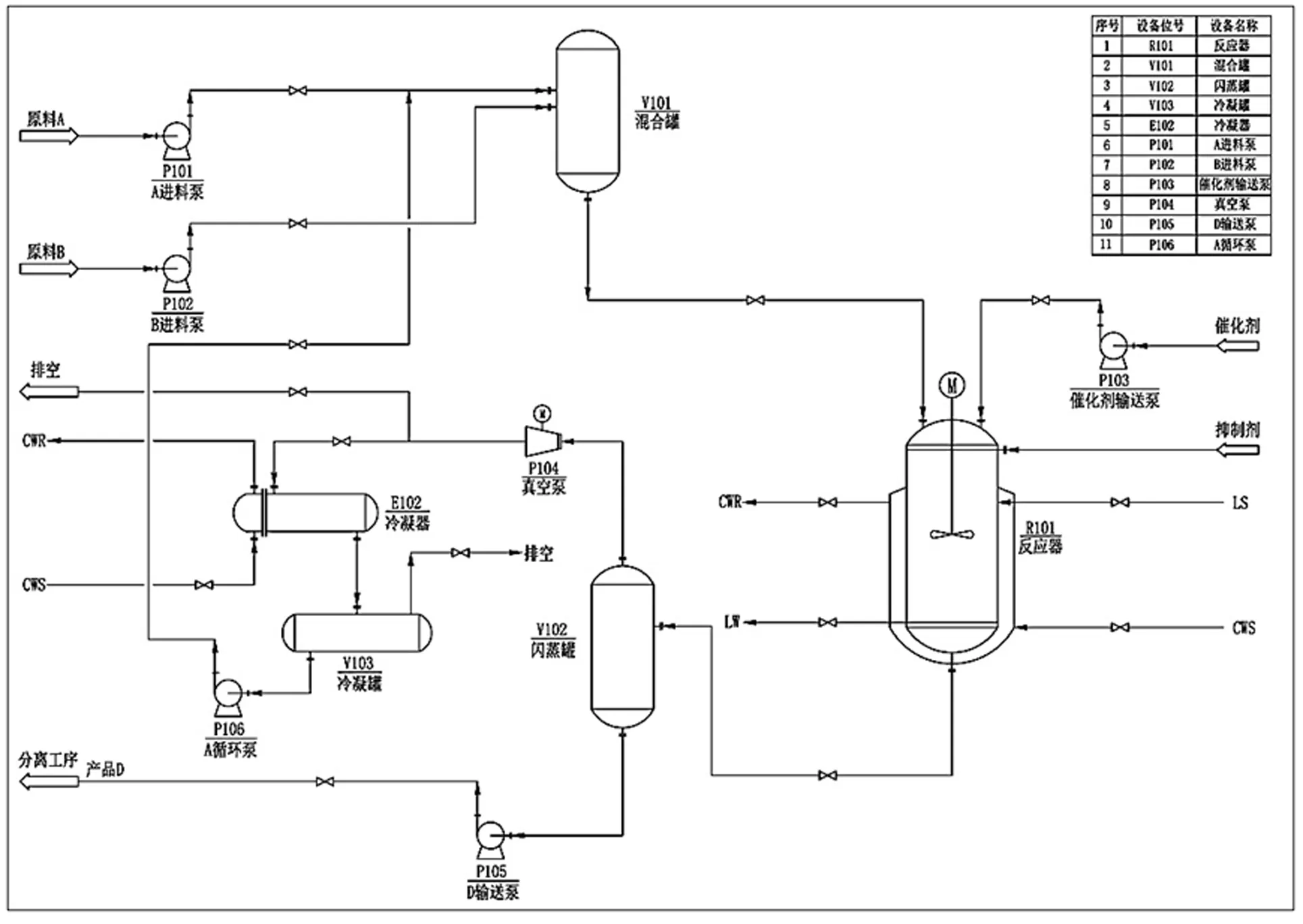
图7 虚拟化工厂工艺流程
3.1 基于SCL语言编写的MFAC控制器
SCL是SIMATIC PCS7系统中用来做算法开发并创建功能块的编程语言。用SCL编写的MFAC的功能块内容包括:定义输入、输出变量,初始化变量,检测实时输出变量,计算输出、输入差值,计算下一时刻伪偏导数和与偏差设定值比较等,最后把得到的MFAC控制块封装如图8所示。
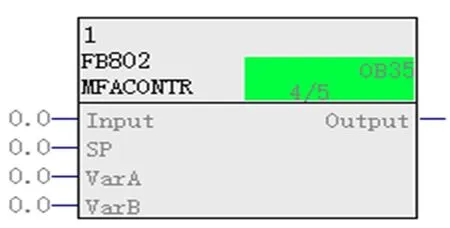
图8 MFAC控制器
MFAC控制器在使用中,只需输入SP、VarA和VarB即可。其中,SP是系统的设定值,VarA和VarB是MFAC需要调整的2个参数,即步长序列ηk和权重因子λ。当λ较小时,系统的响应越快,但是超调量大,系统会失稳;当λ较大时,系统响应变慢,但是超调量小,系统稳定性好,ηk和λ则相反。用MFAC控制器来代替传统的PID控制,并对CFC进行组态后进行虚拟化工厂系统仿真。
3.2 基于虚拟化工厂的MFAC控制器测试
使用MATLAB中的Simulink仿真平台进行图7中的MFAC实验,设定化工厂工艺系统中包括混合罐、反应器、闪蒸罐、冷凝器和冷凝罐等工序,其中最复杂的工序是反应器,包括了放热化学反应的温度、压力、冷却水流量、物料液位等多个参数的控制,分别通过与传统PID调节和MFAC功能块进行控制并比较控制效果。
系统设计包含混合料与催化剂的比值控制系统、双闭环比值控制的串级系统以及流量-温度的串级系统:
(1)混合料与催化剂的比值控制系统的数学模型设定为:
(2)反应器温度控制系统数学模型为:
经过参数整定,副环δ为1.2,Tl为0.6时达到最佳状态,主环的δ为0.92,Tl为0.58时系统达到最佳,系统仿真控制曲线如图9所示。作为对比的副环MFAC的ηk为0.085,λ为1.6,主环的MFAC的ηk为0.094,λ为1.4,系统仿真控制曲线如图10所示。

图9 PID整定仿真图 图10 MFAC仿真结果
为了比较2种方法的抗扰性能,在比值控制系统中,在混合物料的闭环回路中设定方差为0.1,初始种子值为1的扰动,即产生一个幅值为±1的随机扰动。同样在200 s的时候在比值控制系统中加入一个幅值为1的阶跃扰动,在仿真模块图搭建完成后进行仿真。
图9与图10对比结果可以发现, MFAC控制进料系统的调节时间与PID控制系统近似,但是超调量小,曲线平滑。MFAC控制系统在抗扰动性能上,明显优于PID控制系统,且稳定性较高,响应稳定,具有较强的抗干扰能力。
4结论
介绍了MFAC控制算法的原理、性能以及在复杂生产过程中的控制优势。通过PCS7结合SMPT1000流程工业仿真平台和MATLAB仿真平台把MFAC算法应用在虚拟化工厂中,与传统PID控制比较得到令人满意的控制效果。
