大跨度斜拉桥弹性与弹塑性地震响应分析——以广州市洛溪大桥扩建工程为例

杨 慧

广州市中心区交通建设有限公司，广东 广州 510000

自1956年瑞典建成第一座现代斜拉桥Stromsund桥以来，斜拉桥因为良好的受力特点和跨越能力被广泛应用于世界各地的桥梁建设中。但是，斜拉桥跨度的显著提高，一方面对斜拉桥的抗震性能提出了严峻考验，另一方面，我国地震频繁，而斜拉桥又常作为交通枢纽，一旦在地震中受损，会给抢险救灾造成严重困难。因此，进行斜拉桥地震响应分析，掌握其抗震性能，具有重要意义。

文章基于有限元分析平台OpenSees，以广州市洛溪大桥斜拉桥为工程案例，进行动力特性分析、弹性与弹塑性时程分析，对比了结构弹性与弹塑性时程分析的地震位移和内力响应。

1 工程概况

洛溪大桥斜拉桥为半漂浮体系组合梁斜拉桥，全长570m，跨径组成为（30+95+305+110+30）m，斜拉索共有48对，索塔设有一对竖向支座、横向抗风支座和粘滞阻尼器；边墩设竖向支座与横向限位挡块。斜拉桥立面如图1所示。

图1 洛溪大桥斜拉桥（单位：m）

主梁材料为Q345qD钢梁和C60混凝土桥面板，主纵梁为双边箱钢梁，中心距13.4m，标准节段长度为12m；横梁标准间距为4m。桥塔为变异钻石型钢筋混凝土结构，两侧桥塔分别高125.3m和119m。下塔柱分为直线与曲线段，单箱双室变截面；中塔柱高51.8m，单箱单室等截面；上塔柱高35.4m，单箱双室变截面。边墩为矩形墩，横桥向宽3.0m，顺桥向宽2.5m，墩顶处设盖梁。

2 有限元模型

2.1 空间杆系模型

根据震害调查与抗震计算发现，大多数主梁在地震中保持弹性[1]，故按弹性梁柱单元模拟斜拉桥主梁，按“脊骨”模型简化桥面系[2]。边墩盖梁与索塔横梁、拉索锚固区为能力保护构件，在地震中不允许出现损伤，用弹性梁柱单元模拟。将塔墩底部固定，支座用连接单元模拟，设置不同方向刚度值反映实际约束。

用只受拉桁架单元模拟拉索，并定义初应变施加索力。为了考虑垂度效应，通过以下公式折减拉索弹性模量[3]：

式中：Eeq为拉索等效弹模；E为拉索弹模；A为拉索截面积；l为拉索水平投影长度；w为拉索每延米重；T为拉索索力。

2.2 材料本构

采用非线性纤维梁柱单元模拟索塔中、下塔柱和边墩墩柱。划分纤维截面时，通过Steel02定义纵筋，并根据修正Kent-Park模型提高约束混凝土的强度和延性来间接考虑箍筋作用，数学表达式如下：

式中：fc为混凝土应力；εc为混凝土应变；f'c为非约束混凝土圆柱体抗压强度；ε0为非约束混凝土峰值应力下的应变，取0.002；ε20c为混凝土残余应力0.2Kf'c时的应变；K为强度提高系数；Zm为直线下降段的斜率。

Zm的计算公式如下：

式中：ρs为体积配箍率；h"为核心混凝土宽度；Sh为箍筋中间距。

3 动力特性分析

动力特性分析是结构抗震研究的基础，进行地震时程分析前，要掌握桥梁的动力特性。洛溪大桥斜拉桥前10阶振型如表1所示，基本振型云图如图2所示。

表1 斜拉桥前10阶振型

图2 斜拉桥基本振型

通过分析动力特性发现，斜拉桥基本振型为主梁纵漂，基频为0.1652Hz，周期为6.05s，属于长周期结构，并与一般半漂浮斜拉桥的动力特性相符。由于上部结构体系为半漂浮，因此该桥整体较柔，对减轻结构地震响应有利。此外，主梁一阶对称竖弯与横弯振型相近，两者都很大程度上影响结构地震响应，故需要同等重视桥梁纵向与横向抗震性能。

4 弹性与弹塑性时程分析

根据有关桥梁抗震设计规范和工程场地地震效应，选取持时40s、步长0.02s的Ⅱ类场地El-Centro地震波，将峰值加速度调整为0.22g，El-Centro地震加速度时程如图3所示。结构采用瑞利阻尼，阻尼比取0.03，分别沿纵向和横向输入地震动。

图3 El-Centro地震加速度时程

弹性与弹塑性时程分析步骤相同，但弹塑性分析需要建立材料本构，按理想双线性恢复力模型考虑支座的纵向滑动摩擦力。斜拉桥关键位置的峰值位移和内力分别如表2、表3所示。

表2 斜拉桥峰值位移 单位：m

表3 斜拉桥峰值弯矩 单位：kN·m

通过计算发现，纵向地震激发了斜拉桥纵漂模态，塔顶与主梁纵向位移明显，且最大位移出现在右侧主塔顶，为0.154m；而横向地震主要激发主梁横弯与主塔侧弯模态，塔顶和主梁跨中的横向位移明显，最大位移在主梁跨中，为0.16m。因此，纵向地震对主塔影响大，而横向地震对主梁影响大。此外，斜拉桥由纵向地震引起的横向位移和横向地震引起的纵向位移很小，故可认为纵向和横向地震只对各自方向起控制作用。

斜拉桥最大纵向弯矩在右侧塔底截面，为371695kN·m，而最大横向弯矩在左侧塔底截面，为588520kN·m。因此，纵向地震对右侧塔底弯矩影响大，横向地震对左侧塔底弯矩影响大。但两侧塔底的峰值弯矩在横向地震下均比纵向地震大，分别大2倍和1.3倍，说明洛溪大桥斜拉桥的塔底弯矩受横向地震控制。

对比弹性与弹塑性时程分析结果发现，斜拉桥地震峰值位移与峰值弯矩十分接近，这说明结构在给定地震动下塑性发展程度很低，整体未进入塑性，满足弹性要求；而地震峰值弯矩在弹塑性时程分析中略有下降，主要原因是弹性时程分析未考虑保护层混凝土轻微开裂和支座滑动摩擦而耗散的地震能量。此外，边墩峰值弯矩比塔底位置下降更明显，说明边墩弹塑性能预防主塔率先进入塑性。

右侧塔底截面的地震动弯矩-曲率关系如图4所示，斜拉桥关键截面的抗震验算结果如表4、表5所示。

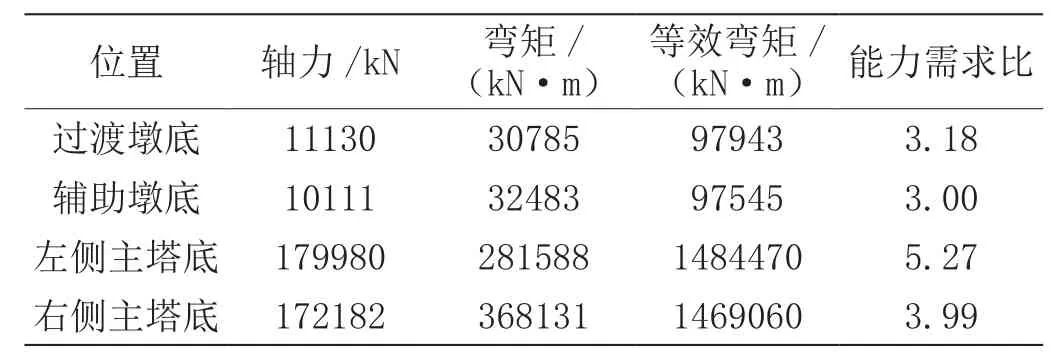
表4 纵向地震截面抗震验算

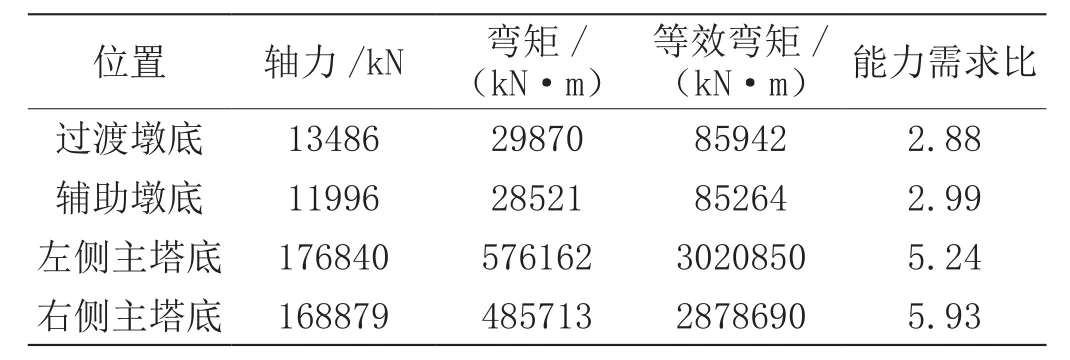
表5 横向地震截面抗震验算

从图4中可以看出，右侧塔底截面地震下的弯矩曲率关系近似线性，说明主塔整体在地震中基本处在弹性范围工作。同时，结构关键截面的抗震验算表明，主塔与边墩的安全储备较大，能较好满足抗震设计要求。

图4 纵向与横向地震右侧塔底截面弯矩-曲率

5 结论

（1）洛溪大桥斜拉桥基频为0.1652Hz，基本振型为纵漂，结构具有柔度大、周期长的特点，对减轻地震作用下的结构内力较有利。

（2）对于结构的峰值位移，斜拉桥主塔受纵向地震影响大，而主梁跨中受横向地震影响大；对于内力响应，结构在横向地震中的内力有了更大程度的提高。但斜拉桥关键截面的抗震验算表明，该桥有较高安全储备来抵抗地震作用，满足E2地震下的抗震要求。

（3）对比斜拉桥地震动位移与内力，结构在给定El-Centro地震动下基本保持弹性，弹性与弹塑性时程分析的地震响应结果很接近。但在计算更大地震动的桥梁响应时，必须考虑结构塑性过程，建立更符合实际的弹塑性有限元模型。