六脉波交交变频器高频段连续变频调速研究
2021-10-25孟耀凯孔丙亚崔占奇冯高明
孟耀凯,孔丙亚,崔占奇,冯高明
(1.河南理工大学 电气工程与自动化学院,河南 焦作 454000;2.平煤股份十三矿,河南 襄城 452670;3.海马新能源有限公司,河南 郑州 450016)
0 引言
三相异步电动机作为最常见的用电设备,已被广泛应用于工矿企业、交通运输、国防工业等各个领域,据统计,异步电动机每年耗电量占全国发电量的50%以上[1]。工业生产中对电机的起动性能要求日益提高,变频技术不仅能够有效调节电动机转速,而且运行效率高,经济效益显著。和交直交变频相比,交交变频没有中间环节,直接进行交流到交流的变换,变换效率较高。交交变频依据余弦交截法截取输入电源的电压片段来逼近基准波,传统的交交变频器输出频率在电源频率的1/3~1/2以下,造成采用交交变频器驱动的电机只能在中速以下运行,调速范围较窄,且其主电路所使用的晶闸管数量较多,在一定程度上增加了变频设备的成本。六脉波双变量交交变频器不仅可以输出传统交交变频器所能输出的所有频率,理论上在25 Hz以上还可输出27.27,30,33.33,37.5,42.85 Hz等5个频段[2-3],且其主电路所使用的晶闸管数量为传统交交变频器的一半,极大节约了变频器的制造成本,并且提升了电动机变频调速的范围。由于六脉波双变量交交变频器的主电路采用零式结构,其本身就包含调压电路,因此在42.85 Hz以上结合工频调压技术,理论上可以实现从低速到高速的全范围、四象限调速。但是实际中,由于在高频段可供截取的电源电压片段数较少,仅靠余弦交截法来决定晶闸管的触发时刻难以保证变频器输出频率的对称度,这就使得高频段的输出波形差,谐波含量多,在电机调速过程中容易引发电机转速和转矩的震荡,甚至无法带动电机运转。因此,在双变量余弦交截法的基础之上,对六脉波双变量交交变频器高频段进行波形优化及对连续变频调速方式进行研究,具有重要的经济价值和工程应用价值。
1 六脉波交交变频器高频段控制原理
1.1 双变量交交变频控制原理
传统的余弦交截法属于单变量相控理论,其计算实质是通过控制移相触发角α对输入的三相或六相电源电压进行片段截取,构成所需要的电压波形[4-5]。双变量控制理论是在单变量控制理论的基础上发展而来的,即在传统的余弦交截法的基础之上增加了对脉冲宽度的控制,其触发角大小的确定和单变量相控理论一样,增加脉冲宽度的控制可以闭锁可能出现的各种环流条件并引导电流换向,从而实现自然无环流的工作方式。触发角和脉冲宽度可以根据实际情况进行调整,其基本控制原则为:(1)当电流为正时(从电源侧流向电动机),给正组晶闸管发触发脉冲,其触发时刻由基准波与同步余弦波的下降沿交点来确定。(2)当电流为负时(从电动机流向电源侧),给反组晶闸管发触发脉冲,其触发时刻由基准波与同步余弦波的上升沿交点来确定。(3)当电流反向时,控制触发脉冲的宽度,以实现自然无环流。(4)当电流为0时,晶闸管的触发时刻可以不受限制[6-7]。
图1为基于双变量交交变频原理所得25 Hz(U相)电压波形原理图,UO为频率25 Hz、换流角60°时,六脉波双变量交交变频器按双变量余弦交截法控制输出的波形,A,B,C,D,E,F为六相互错60°的交流输入电源电压波形,TA,TB,TC,TD,TE,TF为六相输入电源的同步波波形,U为基准波电压波形,I为相应的电流波形。从图1可以看出,基于双变量余弦交截法原理所得25 Hz电压波形UO具有较好的余弦度和对称度。

图1 双变量余弦交截法波形原理图Fig.1 Schematic diagram of bivariate cosine intersection method waveform
1.2 高频段频率切换方式
六脉波双变量交交变频器驱动电机在高频段运行时,需要变频器在不同频率之间进行切换,不同的切换方式对系统的调速性能影响很大,六脉波双变量交交变频器常用的切换方式概括有3种,直接切换方式,固定点切换方式,固定点逐相切换方式[8]。
第一种切换方式在实现上最简单,可以在需要变频时,不考虑上一频段的执行情况立即进行三相频率的切换,但这种切换方式不仅给系统带来一定的冲击,而且在切换过程中也容易产生环流,存在一定的安全隐患,因此实际中很少应用。
第二种切换方式有意识地将频率的切换点选在某一特殊点,比如U相的电压过零点,当需要变频时不是立即切换,而是等到运行至这一特殊点时,再同时进行三相频率的切换,由于切换前后,电压、电流运行状态相近,这种方法在一定程度上减轻了频率切换时对系统的冲击,同时也避免了切换时环流的产生。
第三种方式在切换时考虑到每一相的运行状态,即在U,V,W 三相分别设定一个特殊点,此种方式在频率切换时对系统的冲击最小,但是程序实现较为复杂,在某些情况下会增大频率切换时的最大延迟。
综合考虑以上因素,在高频段变频调速过程中,频段间的切换采用第二种切换方式,即固定点切换方式。
1.3 高频段频率频率值的确定
双变量控制下六脉波交交变频器输出的频率是根据一个周期内基准波所包含的整数个电源波头数得到的,三脉波变频器输出频率为
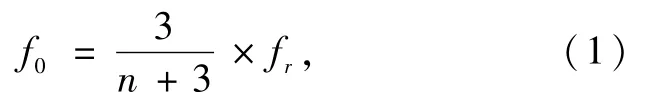
式中:fr为输入频率,取工频电源频率50 Hz;f0为三脉波交交变频器所能输出频段的频率值;n为大于0的整数,表示一个基准波周期能包含的电源波头的数目。
同三脉波交交变频电路类似,六脉波以上的交交变频电路都是以三脉波电路为基础,通过不同的拓扑结构得到的[9]。将三脉波交交变频的规律推广到六脉波交交变频,可以得到式(2),同时推广到b脉波交交变频,见式(3)。
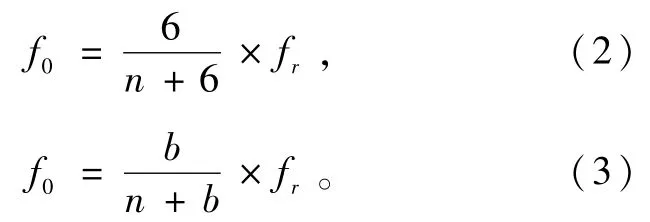
根据式(2),可以得出六脉波双变量交交变频器所能输出的各频段的频率值,在此仅列出25 Hz以上的高频段的频率值,见表1,其中最后一列n0表示变频器输出频率为fr时,其所驱动电动机(4级)相应的同步转速。由表1可以看出,理论上六脉波双变量交交变频器比普通交交变频器在25 Hz以上的高频段可以多输出5个频段,这将使变频器驱动的电动机调速范围有较大的提升。但是也可以看出,高频段基准波一个周期内所包含的波头数较少,即在高频段一个周期内可供变频器截取的电源电压片段数较少,这将导致按双变量理论控制下的变频器输出波形在保证波形余弦度的条件下难以兼顾波形的对称度,使高频段的波形对称度较差,谐波含量较多,尤其是偶次谐波的存在,在电机调速过程中易引发电机转速和转矩的震荡,甚至无法带动电机运转,因此为使变频器更好地驱动电机,需要在双变量余弦交截法的基础之上,对变频器高频段波形进行对称性改造,使变频器输出的波形在具备一定余弦度的同时,也能够具有较好的对称度,使变频器输出波形得以优化,减小谐波含量[10-12]。

表1 六脉波双变量交交变频器输出高频段频率值Tab.1 Six-pulse dual-variable inverter output high-band frequency value
1.4 双变量交交变频器高频段波形优化
由于篇幅有限,本文以频率为33.33 Hz的U相电压为例,说明六脉波双变量交交变频器在高频段晶闸管触发原理。
如图2所示,按照双变量余弦交截法原理获得的33.33 Hz(U相)电压波形图,其换流角为50°。由图2可以看出,在33.33 Hz U相电压的波形中,一个基准波的周期中共包含3个电压片段,整体上看,按双变量余弦交截法原理所截取波形虽然具有较好的余弦度,但是正、负半周的对称性较差,并且不具备基本的奇对称或偶对称,使得变频器输出波形中总的谐波含量增加,而且相应的还会使谐波中的偶次谐波含量增加。为改善变频器输出波形的对称性,在双变量余弦交截法的基础上,通过前移或后移某些电压片段的触发时刻,从而达到改善波形对称性的目的。图3为对称性改造后的33.33 Hz U相电压波形图。

图2 双变量余弦交截法原理图Fig.2 Schematic diagram of bivariate cosine intersection method

图3 对称性改造后变频器输出电压波形图Fig.3 Waveform of inverter output voltage after symmetry transformation
从图3中可以看出,改造后的33.33 Hz U相电压波形对称性明显得到改善,这就使得33.33 Hz这一频段的波形在具备一定余弦度的同时,也兼顾到波形的对称度,使得变频器输出波形得以优化。对于27.27,30,37.5,42.85 Hz的波形优化方式与此类似,这里不再累赘述。
2 高频段变频调速原理
普通交交变频器组成的交流调速系统频率在25 Hz以上通常与调压调速相结合,以实现高频段调速的平滑性及连续性。其在25 Hz以上的调速原理如图4所示,即电机运行在25 Hz条件下,当需要在额定转速条件下运行时,首先向50 Hz低压段U1过渡,随着速度上升,依次逐渐提升工频电压至U2,U3,U4,直至电机转速达到理想的转速为止。这种方法虽然在一定程度上可以扩大高频段的调速范围,但是由25 Hz向50 Hz低压段过渡时,频率级差较大,切换时电压、电流的冲击较大,且电机运行在工频低压条件下,转差功率损耗也较大,因此这种调速效果并不理想[13-15]。
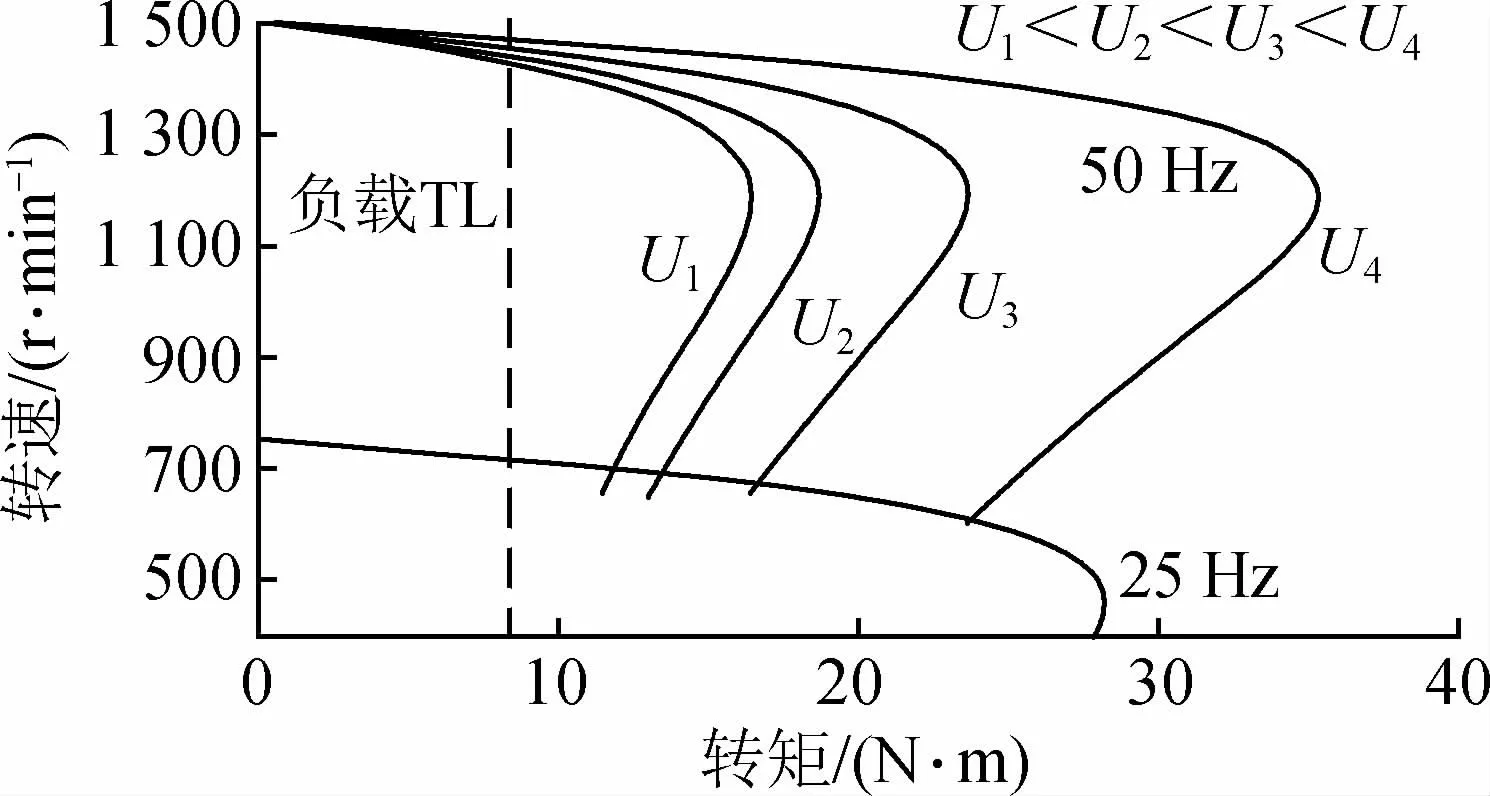
图4 普通交交变频器高频调速原理Fig.4 The principle of high frequency speed regulation of common AC frequency converter
而六脉波双变量交交变频器在25 Hz以上具有相对较多的频段,级差相对较小,在高频段各频段间采用固定点切换方式进行切换,可实现平滑调速。变频器的主电路由U相模块、V相模块和W 相模块组成,每相模块由12个晶闸管分六组反并联组成。晶闸管电路部分采用零式拓扑结构,可靠性较高,并且容易控制。六脉波交交变频器的主电路的结构简图如图5所示。
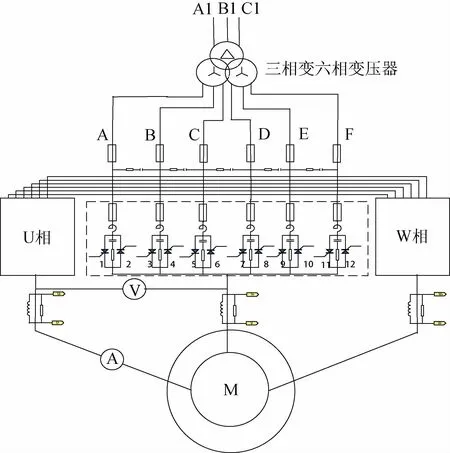
图5 六脉波交交变频器主电路结构简图Fig.5 Schematic diagram of the main circuit structure of the six-pulse AC inverter
由图5可知,变频器的输入电源是由六相互错60°的电源构成,如图5中A,B,C,D,E,F所示,其实是通过三相工频电源A1、B1、C1经三相变六相变压器变换得到的,经过变频器后接入三相交流异步电机进行变频调速。由图5还可以看出,变频器的主接线本身就包含了三相调压电路,故在高频段还可与三相交流调压相结合。其调速原理如图6所示,即电机运行在25 Hz条件下,当需要向额定转速过渡时,首先切换至27.27 Hz,然后随着转速的升高,逐级切换频率,达到42.85 Hz后,此时再结合工频调压技术,向50 Hz频段过渡,直到负载稳定运行在额定转速附近为止。
由图6可以看出,由于六脉波交交变频器在25 Hz以上提供了较多的频段,再结合交流调压技术,从而可以有效扩大高频段调速的范围,且在由25 Hz切换至27.27 Hz,27.27 Hz切换至30 Hz,30 Hz切换至33.33 Hz,33.33 Hz切换至37.5 Hz,37.5 Hz切换至42.85 Hz及42.85 Hz切换至50 Hz的过渡过程中,频率级差明显减小,可以实现平滑连续调速。各频段切换的过程中电压、电流冲击较小,电机的转差功率损耗也大幅度降低,明显优于普通交交变频器在高频段的调速方式。
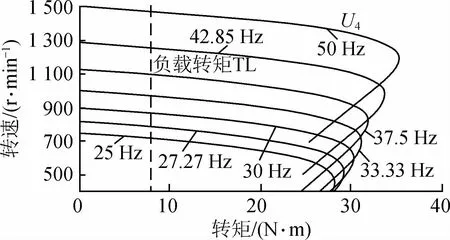
图6 六脉波交交变频器高频调速原理Fig.6 The princip le of high-frequency speed regulation of six-pulse AC inverter
3 仿真研究
3.1 仿真模型搭建
基于六脉波交交变频器工作原理,按照交交变频器主电路结构,在MATLAB/Simulink环境下搭建变频调速仿真模型,如图7所示。
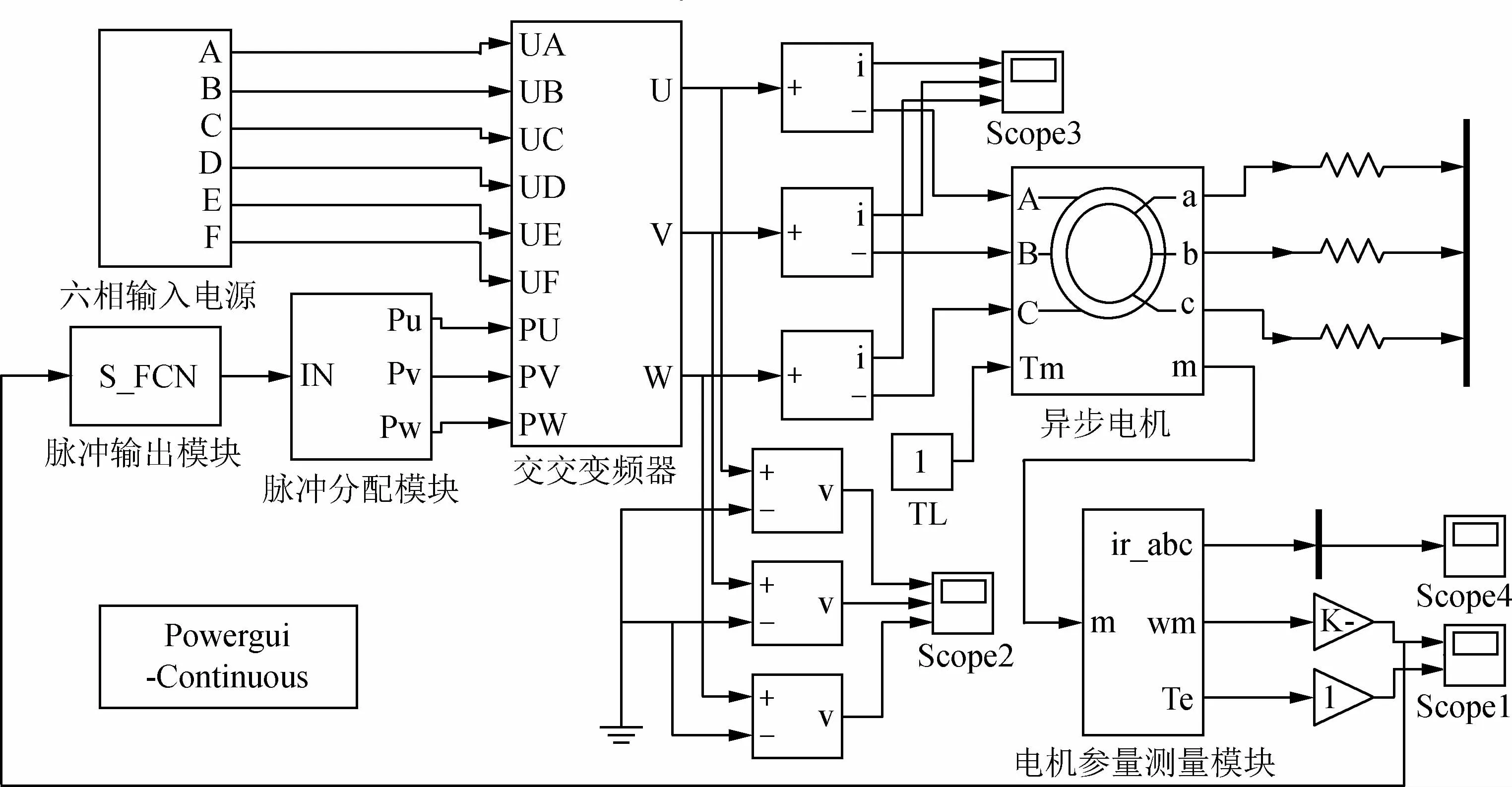
图7 交交变频调速系统仿真模型Fig.7 Simulation model of AC-AC frequency conversion speed regulation system
仿真模型主要包含以下模块:六相输入电源模块、脉冲输出模块、交交变频器模块、三相异步电机模块及其他测量模块。其中,六相电源模块为相位互错60°、频率50 Hz的六相对称交流电源,交交变频器模块一共包含36只晶闸管,其与主电路均采用零式结构,变频器的U相、V相、W相分别由6路反并联的晶闸管组成,分为正反两组,每一相共12只晶闸管。脉冲输出模块主要用来控制交交变频器晶闸管的通断,通过对Simulink中的S函数功能模块进行编程,根据仿真需要向变频器模块输出各相对应的晶闸管触发脉冲及晶闸管编号,并以数组的形式存储,方便程序调用[16-17]。仿真模型中交流异步电机模块的参数为PN=2800 W,UN=380 V,fN=50 Hz,Rr=1.23Ω,Rs=1Ω,ls=0.023 H,lr=0.023 H,lm=0.038 4 H。
3.2 高频段波形对称性改造仿真分析
为了验证变频器波形改造后的效果,将对称性改造后的波形与改造前的波形进行FFT分析,并对其在驱动电机运行方面进行仿真,在此仅以33.33 Hz的U相电压波形为例进行分析。
如图8所示,图8中(a)、(b)分别为按双变量余弦交截法确定晶闸管触发时刻时变频器输出的波形及其FFT分析,图8(c)、(d)分别为对称性改造后的变频器输出波形及其FFT分析。从图8(a)可以看出,改造前的波形对称性不太理想,改造后的波形图8(c)与图8(a)形成对比,图8(c)中的波形对称性明显得到改善。为了更形象说明波形改造前后的效果,结合图8(b)和(d)的FFT分析图可以看出,变频器输出波形的THD改造前为28.83%,改造后为27.09%,波形的总谐波失真下降约2个百分点,再对比波形改造前后谐波成分,可以看出,改造后的波形在偶次谐波及高次谐波方面较改造前均有明显改善。

图8 U相波形图及其FFT分析Fig.8 U-phase waveform and its FFT analysis
图9为用改造后的33.33 Hz波形带动电机运行的转速、转矩波形,电机负载为1 N·m。从转速波形中可以看出,电机转速平稳,整个起动过程转速没有大的震荡,约在1 s时电机转速稳定在980 r/m in左右,且转矩也比较稳定,不存在较大波动。仿真结果说明,通过对称性改造后的变频器波形在电机调速方面具有较好的调速特性。
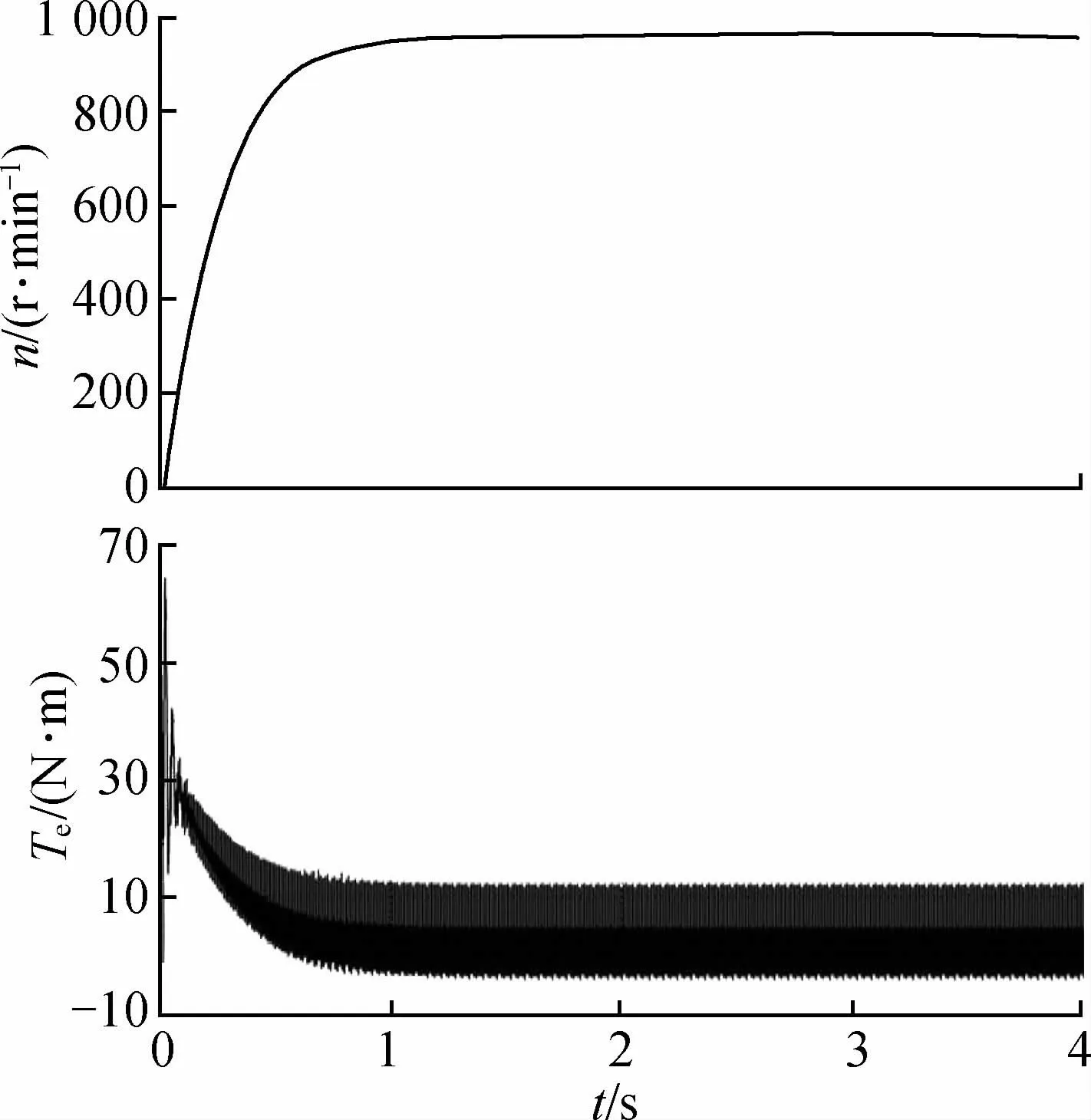
图9 电机转速、转矩波形Fig.9 Motor speed,torque waveform
3.3 高频段频率切换方式及连续变频仿真
在高频段进行连续变频调速时,频率间的切换方式对电机在频率改变时刻的转速过渡过程有着较大的影响。基于此,本文提出频率间固定点切换方式,并在搭建的交交变频调速系统的仿真模型上进行仿真。图10为高频段变频调速过程的转速波形图,仿真中变频器输出电压按恒压频比控制方式确定,电机负载为1 N·m。首先使变频器输出25 Hz频段驱动电机运转,由图10可以看出,启动后1 s左右电机即稳定运行在738 r/min,然后每隔1.5 s左右进行一次频率切换,分别进行25 Hz至27.27 Hz,27.27 Hz至30 Hz,30 Hz至33.33 Hz,33.33 Hz至37.5 Hz,37.5 Hz至42.85 Hz以及42.85 Hz向50 Hz的过渡。随着频率间的切换,电机转速也从738 r/min逐渐过渡至1 440 r/m in左右稳定运行。由图10可以看出,从25 Hz到50 Hz各频段间的过渡较为平滑,转速上均不存在较大震荡,在高频段进行连续变频的效果很好。
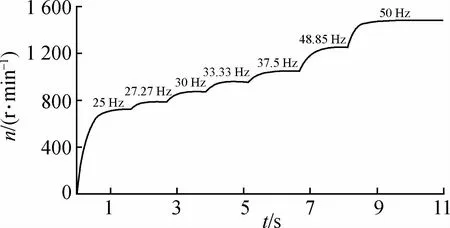
图10 连续变频转速波形Fig.10 Continuous frequency conversion speed waveform
由于篇幅有限,仅对33.33 Hz与37.5 Hz间的切换过程为例进行分析。图11为33.33 Hz向37.5 Hz切换过程中U,V,W 三相电压波形,频率切换过程中选择U相电压过零点为频率切换时刻。由图10可以看出,在5.1 s之前电机运行在33.33 Hz,转速为950 r/min左右,5.1 s时开始进行频率切换,由图11的三相电压波形可以看出,切换前后U相、W 相电压过渡较为平滑,V相电压在经过0.005 s的短时震荡后也迅速的过渡至37.5 Hz,在5.11 s时三相电压变频过渡结束,变频器开始以37.5 Hz的频率驱动电机运行。结合图10频率切换过程中的转速波形可以看出,在频率切换过程中,速度过渡较为平滑,几乎没有大的震荡,仿真结果说明高频段采用固定点切换方式进行频率切换是可行的。
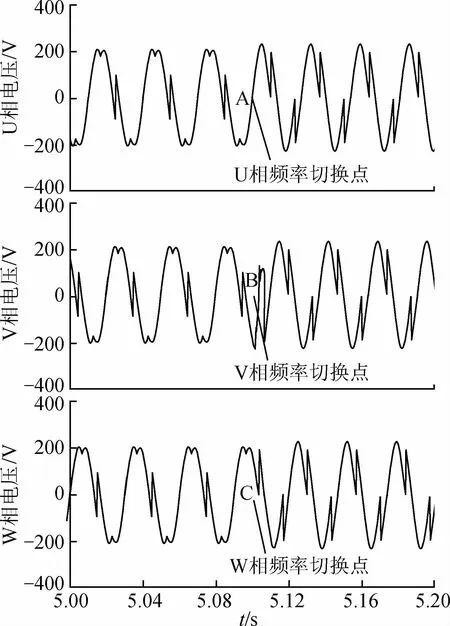
图11 变频过程电压波形Fig.11 Voltage waveform during frequency conversion
4 实验研究
前文通过仿真验证了六脉波交交变频器高频段变频调速的可行性,接下来在六脉波交交变频调速系统实验平台上对高频段调速理论进行实验验证。实验中所用电机型号为西门子1LA7-113M-4AA型,铭牌参数PN=4 kW,UN=380 V,IN=8.4 A,nN=1 440 r/min。试验中电压波形用HS801虚拟示波器进行采集,转速曲线通过上位机进行实时显示。图12为变频器输出25 Hz、带载3.2 N·m时电机的U相电压波形图。

图12 变频器输出25Hz(U相电压)波形图Fig.12 Waveform of the inverter output 25 Hz(U-phase voltage)
由图12可以看出,六脉波双变量交交变频器输出的波形具有较高的对称度和余弦度,且通过图13电机的转速波形可以看出,在25 Hz条件下,电机运行较为平稳,启动1 s左右电机稳定运行在738 r/min,转差降落约为10 r/min,电机的启动特性及稳定运行特性较为理想。

图13 电机运行在25 Hz条件下转速曲线Fig.13 Speed curve ofmotor running at 25 Hz
为验证六脉波双变量交交变频器在25 Hz以上各频段的运行特性及变频调速特性,在试验中每隔一段时间进行一次变频,图14为高频段连续变频时的转速波形图,首先使变频器输出25 Hz驱动电机运转,由图14可以看出,启动后1s左右电机即稳定运行在738 r/m in,然后每隔6s左右进行一次频率切换,分别进行25 Hz至27.27 Hz,27.27 Hz至30 Hz,30 Hz至33.33 Hz,33.33 Hz至37.5 Hz,37.5 Hz至42.85 Hz以及42.85 Hz向50 Hz的过渡,随着频率间切换,电机转速也从738 r/m in逐渐切换至1 440 r/m in稳定运行。
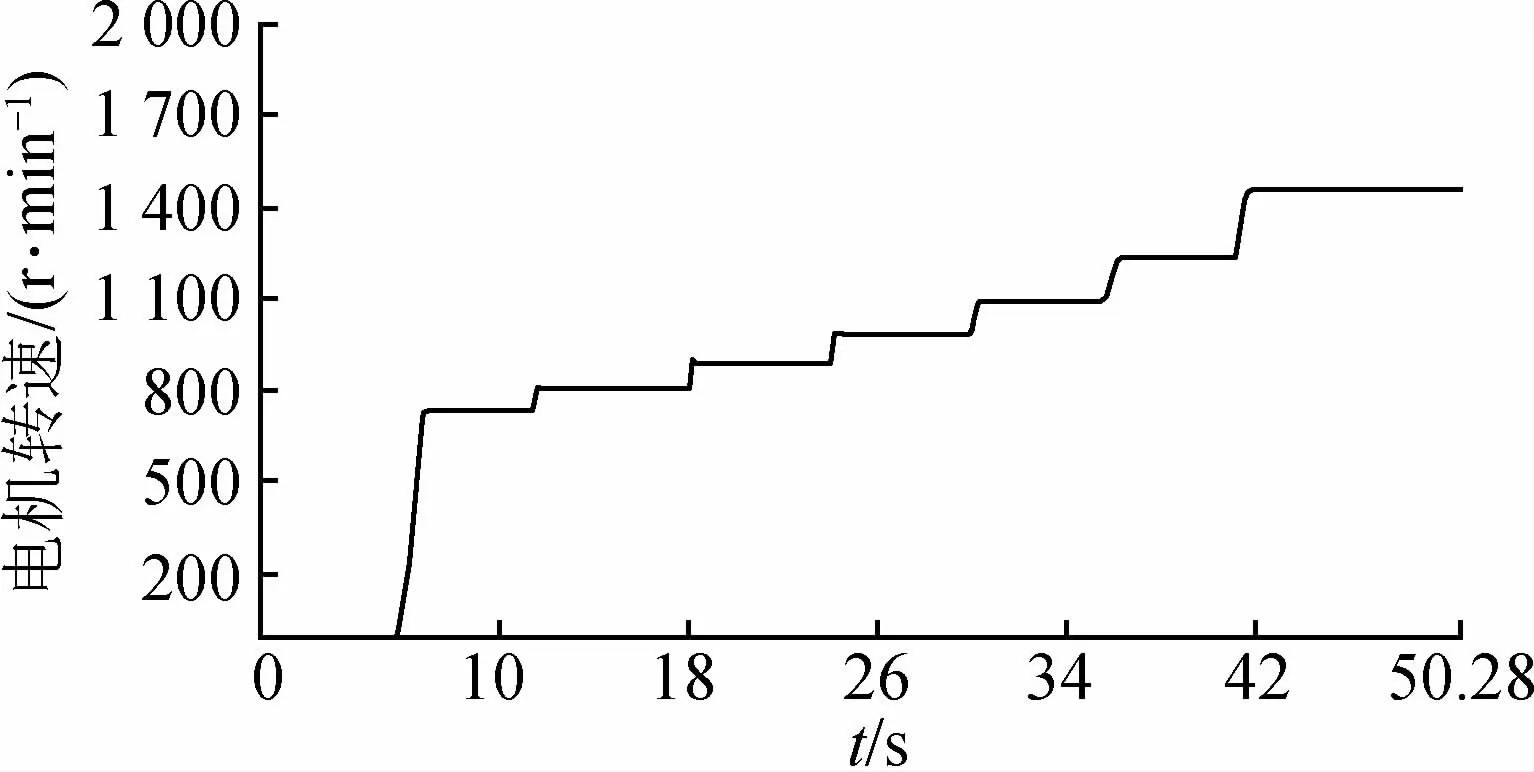
图14 高频段连续变频调速波形图Fig.14 High frequency band continuous frequency conversion speed control waveform
由图14可以看出,在各频段电机均能稳定运行,整个切换过程相对平滑,震荡较小。实验结果与仿真结果相一致,即六脉波双变量交交变频器在高频段进行变频调速时,具有较好的调速特性,且由于各频段间级差相对较小,在频率切换的过程中,系统电压、电流的冲击较小,电机转速震荡较小,运行较为平稳。
5 结论
(1)在双变量余弦交截法的基础之上对变频波形进行改造,可有效改善波形的对称度,从而减小变频器输出波形的谐波。
(2)在高频段进行变频调速,针对高频段频率之间的切换方式,提出了在高频段采用固定点切换的方式。
(3)对高频段变频调速进行仿真和实验验证,结果表明,本文的六脉波交交变频器高频段变频调速方法具有一定的可行性。
