LTE D2D频偏估计算法及其仿真分析*
2021-10-25徐子龙刘为温文坤闵铁锐唐瑞波王琳
徐子龙,刘为,2**,温文坤,闵铁锐,2,唐瑞波,王琳
(1.中国电子科技集团公司第七研究所,广东 广州 510310;2.中国电子科技集团公司新一代移动通信创新中心,上海 200331;3.广州技象科技有限公司,广东 广州 510310)
0 引言
LTE(Long Term Evolution,LTE 长期演进)的D2D(Device to Device,设备间通信)协议,允许一个UE(User Equipment,用户设备)和一个或多个用户设备直接通信。相互通信的两个UE 都可能存在频偏,二者叠加后,频偏可能进一步增大。D2D 设备的初始频偏与载波频偏之比位于±10 ppm 范围内[1],D2D 支持的最高频带为3 410—3 490 MHz[2],因此频偏范围最大可达±34.90 kHz。如何提高频偏估计范围(同时兼顾估计精度)成为D2D 系统设计的一个重要挑战。
D2D 的参考序列具有两段重复特性,利用参考序列的重复性进行频偏估计业界已有研究成果。文献[3] 提出利用循环前缀的重复性进行频偏估计,由于循环前缀长度较小且受符号间干扰,其估计性能较差;文献[4]设计了一种特殊的前导结构——在一个正交频分复用(OFDM,Orthogonal Frequency Division Multiplexing)符号中包含两段重复的符号序列,用于估计小数倍频偏和整数倍频偏,因循环前缀消除了码间干扰的影响,小数倍频偏估计性能稳定,然而其整数倍频偏估计算法依赖于原文给出的特定前导结构,因而不能直接应用于D2D 场景。
本文以LTE D2D 为应用场景提出了一种先估计小数倍频偏、后估计整数倍频偏的频偏估计方案。小数倍频偏估计算法利用了D2D 同步信号周期性及其结构的重复性,优化了估计精度;整数频偏的估计范围可以按需调整(粒度为小数倍频偏算法的估计范围),解决了LTE D2D 系统需要估计大频偏的问题。
1 系统模型
D2D 的PSSS(Primary Sidelink Synchronization Signal,主同步信号)和SSSS(Secondary Sidelink Synchronization Signal,辅同步信号)以40 ms 为周期[5],由两个连续且相同的SC-FDMA(Single-Carrier Frequency Division Multiple Access,单载波频域频分多址)符号组成[6],即PSSS 和SSSS 均具有两段重复特性,如图1 所示。
本文分析和仿真采用的模型为:

其中x(i)表示发端等效基带信号的第i个采样点,r(i)为相应的接收信号,α(l)为信道抽头系数,其统计特性取决于信道模型,Ts表示采样间隔,l表示信道抽头时延(单位为Ts),L表示多径数量,ε表示频率偏差(Hz),w(i)为零均值复高斯白噪声。式(1)中的任意频偏ε可表示为:

其中εint=kεB(k为某一整数)表示整数倍频偏值,εfract(-εB/2﹤εfract≤εB/2)表示小数倍频偏值,εB为下文所述小数倍频偏估计范围。
2 本文算法
2.1 小数倍频偏估计
本文利用PSSS 和SSSS 符号的两段重复性和周期性来计算小数倍频偏。如图1 所示,在第m个PSSS/SSSS周期内,用表示第一个PSSS 符号的CP 的起始位置,NCP表示循环前缀(CP, Cyclic Prefix)包含的采样点数,则接收的第一个PSSS 符号可表示为:
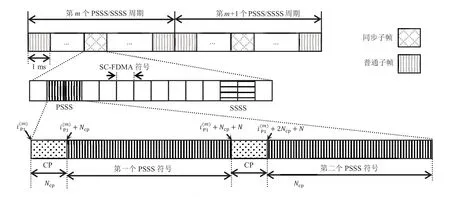
图1 PSSS/SSSS符号的周期、两段重复特性示意图

第二个PSSS 符号表示为:
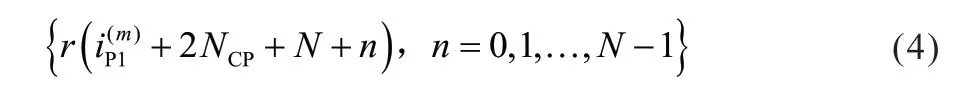
其中N为符号(不含CP)包含的采样点个数。这两个PSSS 序列的相关函数定义为:
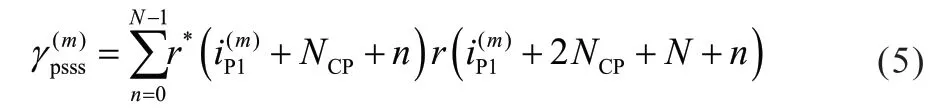
与PSSS 完全类似,在第m个PSSS/SSSS 周期内,两个SSSS 序列的相关函数定义为:
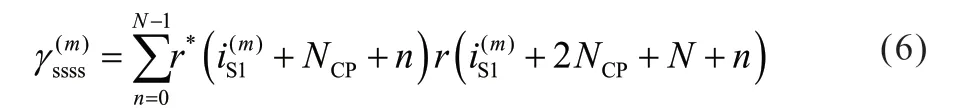

其中M表示用到的PSSS/SSSS的周期个数,arg{x}表示x的相角。
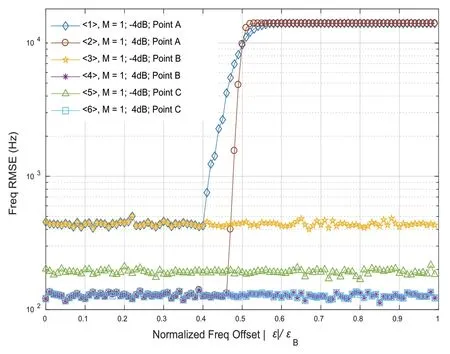
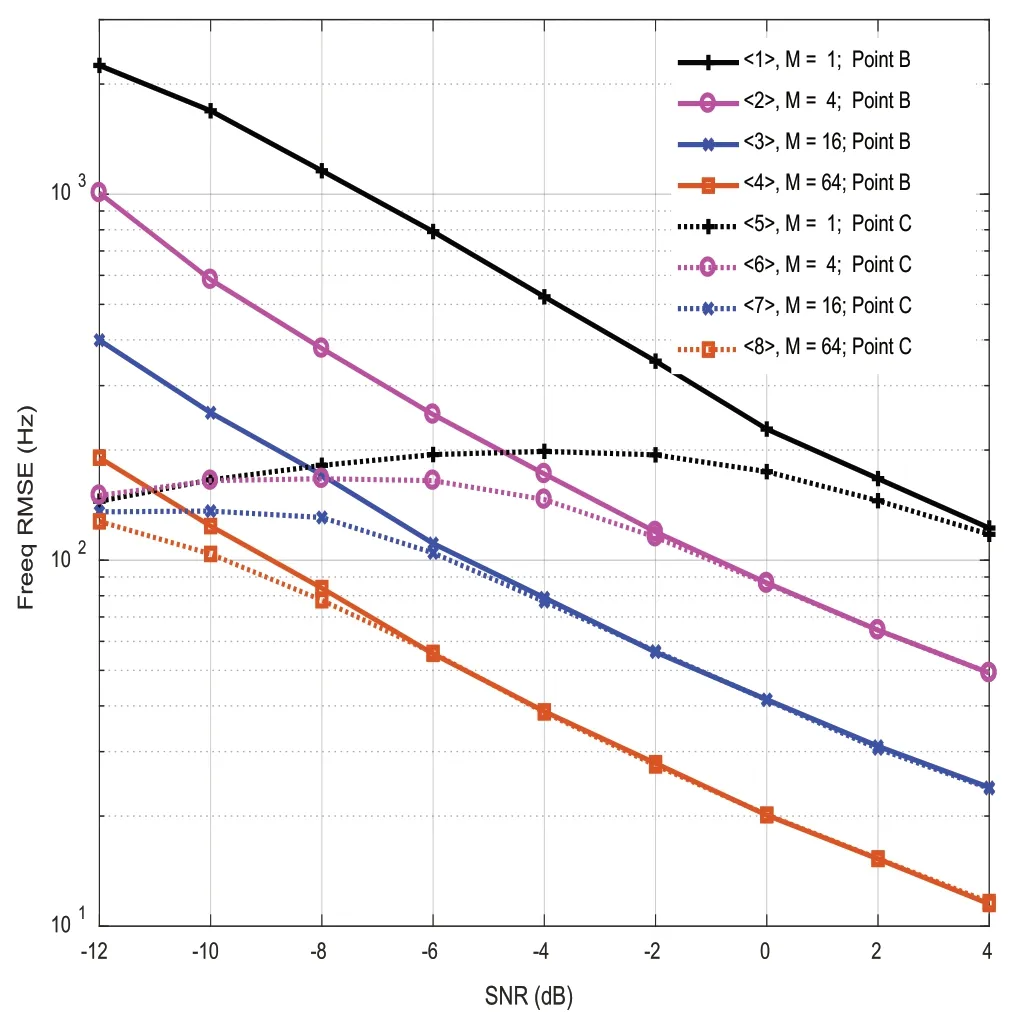
考虑到-π 式(8) 的区间长度定义为小数倍频偏估计范围: 不失一般性,将式(2)中k的取值范围限定为,其中K为可按需配置的正整数,其取值越大意味着可估计的频偏的取值范围越大。对于D2D 系统,因为,足以覆盖D2D 系统所要求的最大频偏范围-34.9~34.9 kHz,因此下文假定K=2。 式(2) 表明用小数倍频偏εfract对接收信号进行频偏补偿后,残余频偏为整数倍频偏kεB,其中k是唯一待定参数。本文根据PSCCH(Physical Sidelink Control Channel,侧链控制信道)解码成功与否,即根据PSCCH 内置的CRC(Cyclic Redundancy Check,循环冗余校验)是否通过来确定k的取值。如图2 所示,整数倍频偏估计(即对k值的估计)按下述步骤进行: 图2 仿真链路/整数倍频偏估计和补偿 (2)初始化k=-K。 (5)若PSCCH 解码失败则转到步骤(4)。 (6)如果k≤K,则k=k+1,回到步骤(3),否则认为整数倍频偏估计失败,在下一个PSCCH 到来之时重新执行步骤(1)。 考虑到小数倍频偏的真值 fractε接收机是未知的,此处用取代fractε,这会引入估计偏差,导致残余频偏位于附近。 图2 为仿真链路图,其中D2D 基带信号模块包含了产生D2D 基带信号的所有流程,如PSCCH 处理流程、同步信号PSSS/SSSS 产生、SC-FDMA 调制等。仿真用到两种信道模型:AWGN(Additive White Gaussian Noise)和EVA(Extended Vehicular A model),其 中EVA 为文献[2] 的Table B.2.1-3 定义的衰落信道模型。若选用AWGN 信道模型,图2 的衰落信道模块不起作用。小数倍频偏估计算法见2.1 节,整数倍频偏估计算法见2.2节。PSCCH 解码流程可参考文献[7],其中包含CRC 校验过程,此CRC 校验结果将用于确定整数倍频偏估计值。 以下仿真假定两个无网络覆盖的UE 进行D2D 通信,参数汇总于表1。 表1 参数约定 为了评估算法性能,我们考察图2 中测试点A、B和C 处的频偏估计的RMSE(Root-Mean-Square-Error,均方根误差)在不同的信噪比条件下随归一化频偏ε/εB的变化趋势。A 点的RMSE 表示的均方误差;C 点的RMSE 表示CRC 校验成功时对应的频偏估计值的均方误差。B 点(信道均衡器输入端)在CRC 校验之前,尚不知整数倍频偏取值,为了与A 和C进行有意义的比较,将B 点处的RMSE 定义为信道均衡器输入端看到的最小残余频偏的均方根误差,其中。仿真采用AWGN 信道,假定频偏ε在范围内均匀分布,其它参数如表1 所示。 分析图3 可以得出以下结论: 图3 频偏估计的RMSE随归一化频偏变化图(AWGN) (3)曲 线﹤3>﹤4>(或﹤5>﹤6>)的RMSE 均 随SNR 增加而下降且几乎不受取值变化的影响,这是因为B 点处的RMSE 定义,相当于完成了最佳整数倍频偏估计。当SNR=-4 dB 时,频偏估计值偏差较大的样本容易导致CRC 校验错误而未被计入C 点的RMSE 中(相当于CRC 模块“滤除”了这个估计偏差较大的样本),所以曲线﹤5>比﹤3>的RMSE 小;当SNR=4 dB 时,频偏的RMSE 足够小,SNR 足够大,CRC 几乎全对(此时几乎无被“滤除”的样本),于是﹤4>和﹤6>的曲线几乎重合。由于CRC 的“过滤”作用,测试点C 的RMSE不超过测试点B 的RMSE。 图4 给出了M 取不同值时RMSE 随SNR 的变化趋势,仿真采用EVA70 信道模型,假定频偏ε 在范围kHz 内均匀分布,其它参数如表1 所示。 由图4 可以得出以下结论: 图4 频偏估计的RMSE随信噪比SNR变化图(EVA70+AWGN) (1)比较曲线﹤1>、﹤2>、﹤3>和﹤4>,可知M取值越大测试点B 处的RMSE 越小。 (2)比较曲线﹤1>和﹤5>、﹤2>和﹤6>、﹤3>和﹤7>以及﹤4>和﹤8>,可知当取值相同时,测试点C 的RMSE 比测试点B 处的RMSE 小。因为CRC 校验模块“滤除”了因估计偏差较大而导致CRC 校验出错的样本。 (3)观察虚线﹤5>、﹤6>、﹤7>和﹤8>,发现一个有趣的现象:当SNR 小于某个值(例如M=64 时,SNR=-2 dB;M=16 时,SNR=-6 dB)时,随着信噪比降低,RMSE 不升反降,即SNR 和RMSE 程正相关。这是因为CRC 校验成功与否同时受到频偏和SNR 这两个因素的影响。一般地,SNR 越低,CRC 校验通过的可能性越小;残余频偏越大,通过CRC 校验的可能性也越小。因此,在SNR 较小时,只有残余频偏也相应地较小,CRC 校验才有望通过,而频偏估值偏差过大的样本因CRC 校验出错被检测出来并抛弃了,因此出现前述SNR 与RMSE 呈正相关的“反常”现象,这意味着通过CRC 校验的频偏估计值是更精确的。 图5 的(a)和(b)分别给出了在AWGN 和EVA70信道下频偏估计/补偿模块对BLER(Block Error Rate,误块率)曲线的影响。仿真假定频偏ε在[-35,35] kHz 范围内均匀分布,采用MMSE 频域均衡算法,其它参数如表1所示。随机选取的每个频偏可仿真得到一条BLER 曲线,图中的BLER 是若干个随机选择的频偏对应的BLER 曲线取平均的结果。频偏估计和补偿规则为:利用最新接收的连续M个周期的同步信号进行估计和补偿,若频偏估计成功(CRC 校验通过),则立即更新频偏估计值,否则沿用之前成功获取的频偏估计值。 由图5 可得以下结论: 图5 频偏估计/补偿模块对BLER的影响 (1)频偏未补偿时(图例为“Raw”),BLER 取值趋于1 且与SNR 无关。 (2)M取值越大BLER 性能越好,这是因为随着M的增大频偏估计的RMSE 相应地减小(见图4),由频偏引起的CRC 解码出错概率相应地降低。 (3)在AWGN 信道下,当SNR≤-4 dB 时,M=32或64 对应的曲线与参考曲线相差小于1 dB。在EVA70信道下,当M=8 时与参考曲线性能相差小于0.5 dB,当M=64 时,二者性能几乎相同。可见,本文所提频偏估计算法在AWGN 或EVA70 下相比参考方案的性能损失不超过1 dB。图例标识为“图例标识为案的性能损的参考曲线表示无频偏时的性能曲线”。 本文提出的频偏估计算法的频偏估计范围可调整,调整粒度为小数倍频偏估计范围,解决了D2D 系统要求估计大频偏的问题,频偏估计精度可通过增大观测周期数来提升,满足了系统对频偏估计精度的需求,此外,因估计偏差过大引起CRC 校验出错的估值可以被发现和滤除,使得在SNR 较小时仍能获得精确的频偏估计值。算法的整数倍频偏估计包含盲尝试,小数倍频偏估计包含多个D2D 周期,时延较大,未来将在降低时延方面做进一步研究。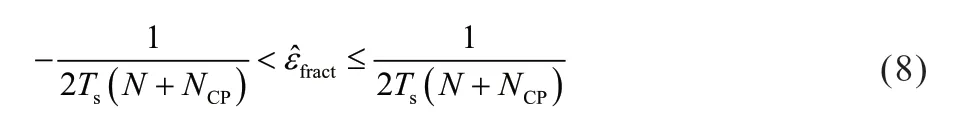

2.2 整数倍频偏估计

3 仿真分析
3.1 仿真链路介绍

3.2 频偏估计的均方根误差与频偏的关系
3.3 频偏估计均方根误差与信噪比的关系
3.4 频偏估计和补偿模块对误块率的影响

4 结束语
