On Existence of Local Solutions for a Hyperbolic System Modelling Chemotaxis with Memory Term

WU Shaohua and WANG Pengfei

School of Mathematics and Statistics,Wuhan University,Wuhan 430072,China

Abstract. In this paper,we discuss the local existence of weak solutions for some hyperbolic parabolic systems modelling chemotaxis with memory term.The main methods we use are the fixed point theorem and semigroup theory.

Key Words:Hyperbolic-parabolic system;KS model;chemotaxis;memory term.

1 Introduction

The earliest model for chemosensitive movement has been developed by Keller and Segel in[1],which is described by the following parabolic system:

whereurepresents the population density andvdenotes the density of the external stimulus,χis the sensitive coefficient,the time constant 0 ≤τ≤1 indicates that the spatial spread of the organismsuand the control signalvare on different time scales.The caseτ.=0 corresponds to a quasi-steady-state assumption for the signal distribution.Since the KS model is designed to describe the behaviour of bacteria and bacteria aggregates,the question arises whether or not this model is able to show aggregation.Plenty of theoretical research uncovered exact conditions for aggregations and blow-up [2–16].Besides,free boundary problems for the chemotaxis model are considered[18–25].

The possibility of blow-up of the solution for the KS model has been shown to depend strongly on space dimension.For instance,in the case ofχis constant andg(u,v)=γu−δu,finite-time blow-up never occurs in 1D case[26] (unless there is no diffusion of the attractant v,[27,28]),but can always occur in N-dimensional cases forN≥3.For the 2D case,it depends on the initial data,i.e.there exists a threshold;if the initial distribution exceeds its threshold,then the solution blows up in finite time,otherwise the solution exists globally[29].

It is well-known that the movement behaviour of most species is usually guided by external signals,such as amoeba move upwards chemical gradients,insects approach towards light sources,the smell of a sexual partner makes it favourable to choose a certain direction.Motivated by these examples,if the external stimulus is based on the light(or the electromagnetic wave),then the control equation (1.2) should be replaced by a hyperbolic equation:

where,e.g.if the external signal is the electromagnetic field,then v would be voltage(in this case,∇vdenotes the electromagnetic field).

In this case,the full system foruandvbecome the following hyperbolic parabolic system:

We introduce a memory term in equation(1.1),i.e.

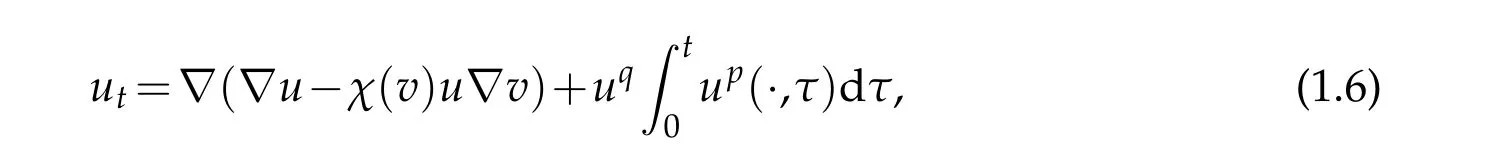
wherep,q≥0 are nonnegative constants.

Letg(u,v)=−γv+f(u),χ(v)=χis a constant,and supplement equations(1.5),(1.6)with some initial boundary conditions,then we obtain the following system

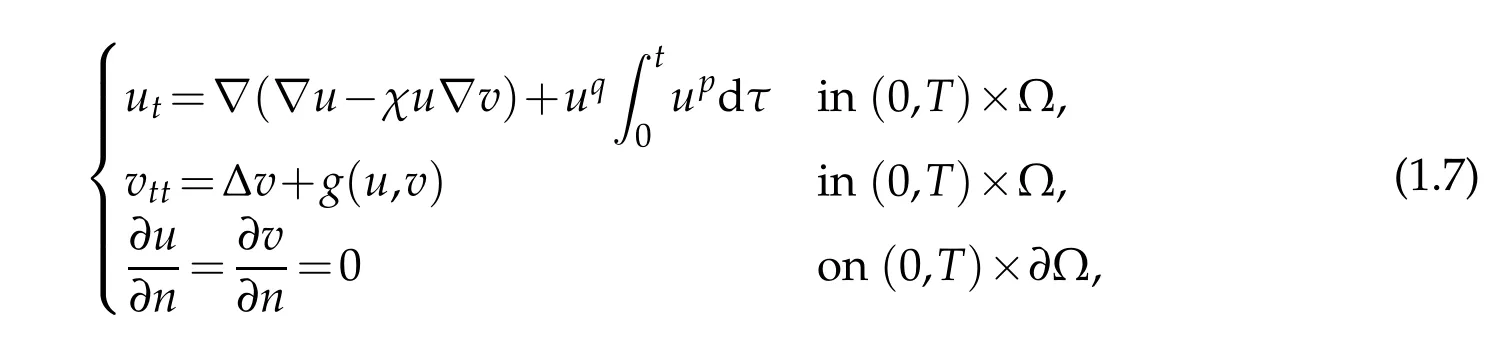
with initial data

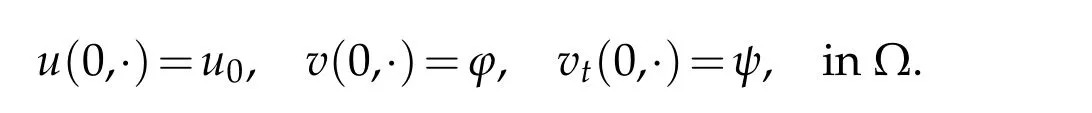
wherep≥0,q≥0,Ω ⊂RN,a bounded open domain with smooth boundary∂Ω,nis the unit outer normal on∂Ω andχis a nonnegative constant.

In this paper we would discuss the case ofp=1,q=0.

2 Main results

Let us consider the following system:

with initial data

Choose a constantσwhich satisfies

It is easy to check that(2.2),(2.3)can be simultaneously satisfied in the case of 1≤N≤3.

Our main results are the following.

Theorem 2.1.Under conditions(2.2)and(2.3),if g(u,v)=−γv+f(u)and f∈C2(R),then for each initial dataand ψ∈H1(Ω),problem(2.1)has a unique local solution(u,v)∈

We define here

Here,u(x,t)∈C([0,t0],means that

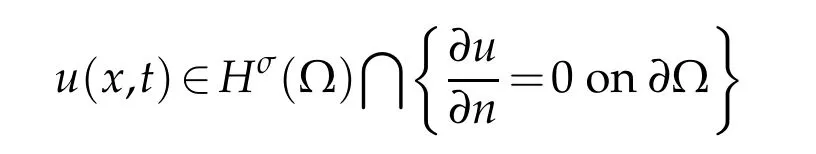
for eacht∈[0,t0]and‖u(t,·)‖Hσ∈C([0,t0]);u(x,t)∈C1([0,t0],H1(Ω))means thatu(x,t)∈C1([0,t0],H1(Ω))andut(x,t)∈C1([0,t0],H1(Ω)).

Observe that the conditions forfin Theorems 2.1 can be weakened tof∈C1andfis bounded on R.

Remark 2.1.We cannot deduce the nonnegativity of the solutions even in the case off(0)=0.

3 Some basic lemmas

Forg(u,v)=−γv+f(u),andγis a constant,f∈C2(R).We divide system(2.1)into two parts:

We have the following lemmas.

Lemma 3.1.For any T>0and

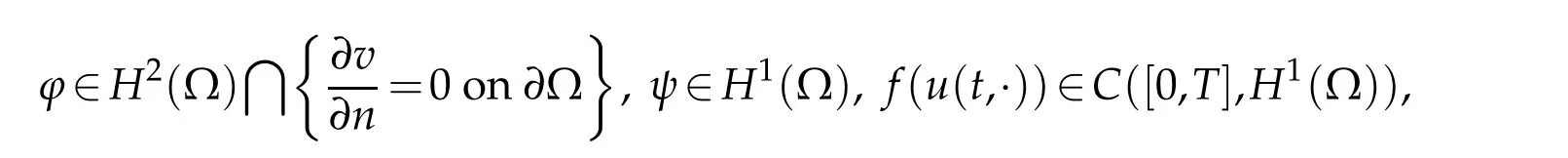
(3.2)admits a unique solution v,satisfying

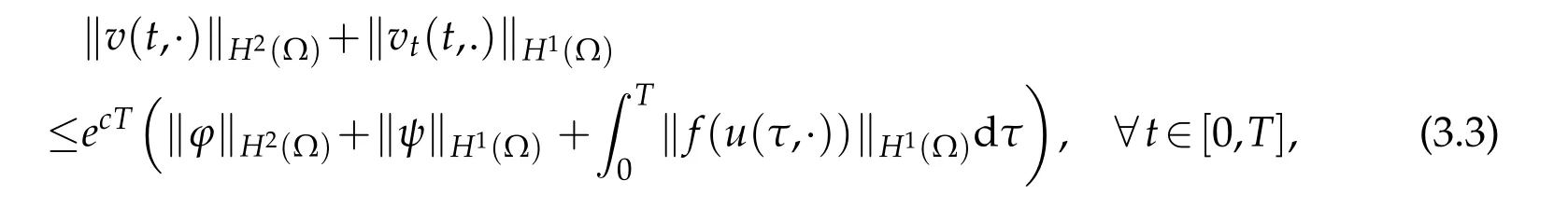
where c>0is a constant which is independent of T.

Proof.Settingvt=w,we have the following system:

Thus,we can write it in an abstract form

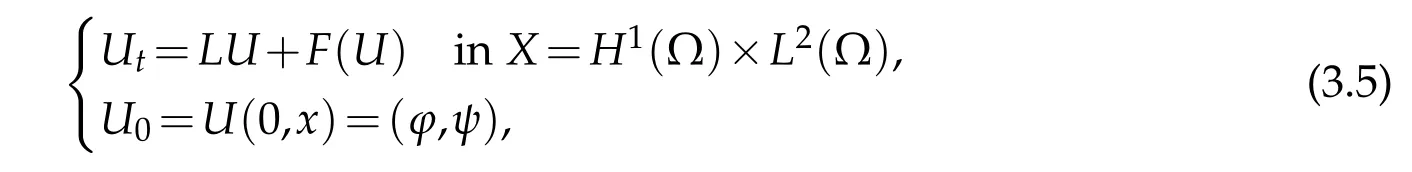
whereL(v,w)=(w,∆v−v)for(v,w)∈D(L),andF(v,w)=(0,(1−γ)v+f(u)).

Define the inner product inXas

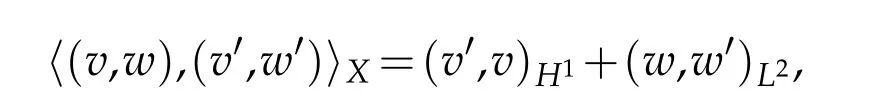
where(·,·)H1and(·,·)L2represent the inner products inH1andL2,respectively,thenXis a Hilbert space.

ForU=(v,w)∈D(L),we have

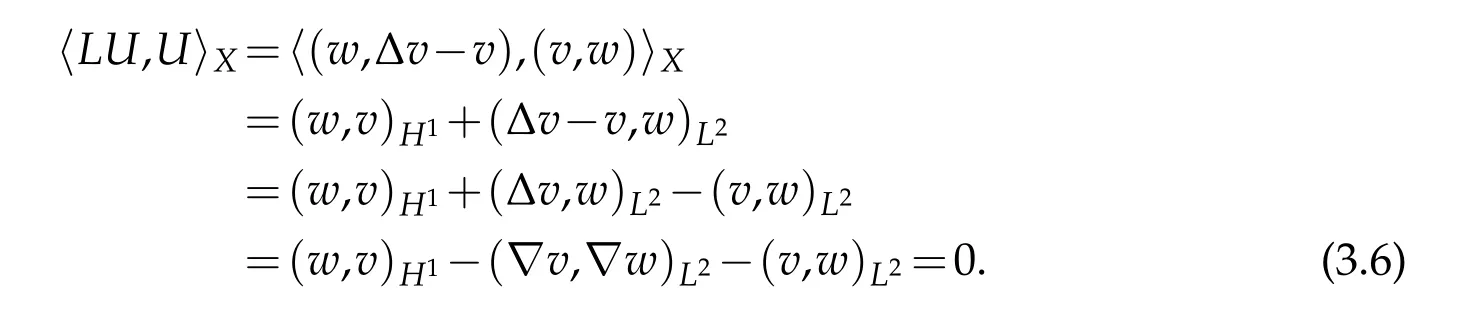
Otherwise,forU=(v,w)∈D(L)andU′=(v′,w′)∈X,

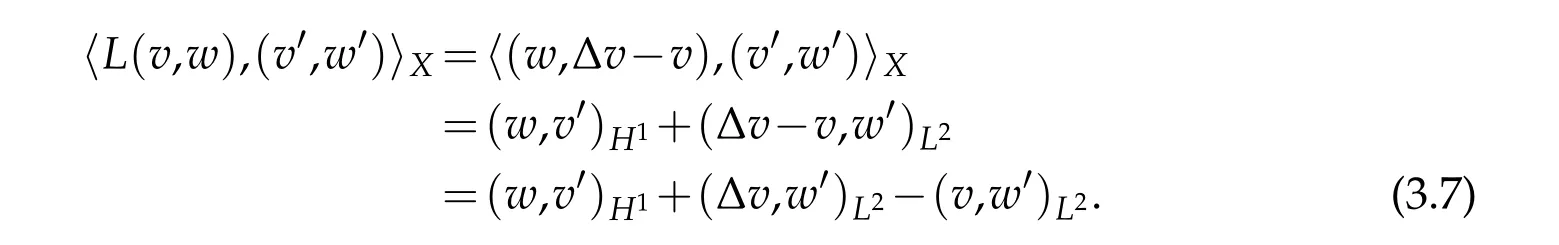
If 〈L(v,w),(v′,w′)〉Xis bounded for each (v,w)∈D(L),then(w,v′)H1,(∆v,w′)L2and(v,w′)L2are bounded for each(v,w)∈D(L),which means that

which impliesD(L∗)⊂D(L).On the other hand,in view of (3.6) and the Lemma in Haraux(p.9),we conclude

Therefore,Lis a generator of a unitary operator group.It is easy to check that forf(u(t,·))∈C([0,T],H1(Ω)),

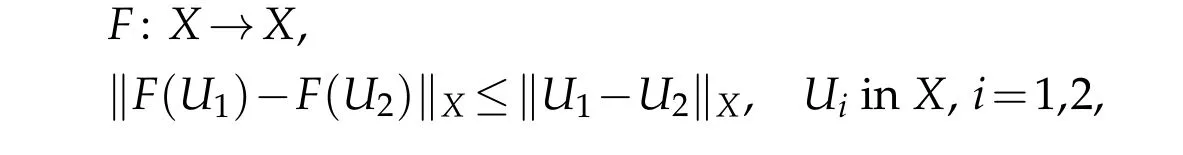
where‖(v,w)

Now we can declare that(3.5)has a unique solution

which means that for each(ϕ,ψ)∈D(L),(3.5)admits a unique solution

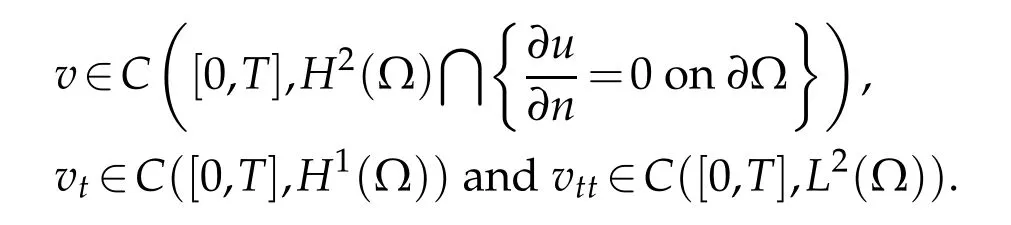
Next,we estimate the norm ofv.By using the semigroup notationT(t)=etL,we have

SinceL∗=−L,and in terms of(3.6),we know

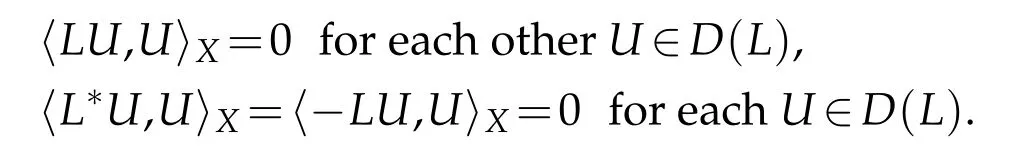
Hence,Lgenerates a strongly continuous contractive semigroup on the Hilbert spaceX[17,32];in other words,we have

Consequently,

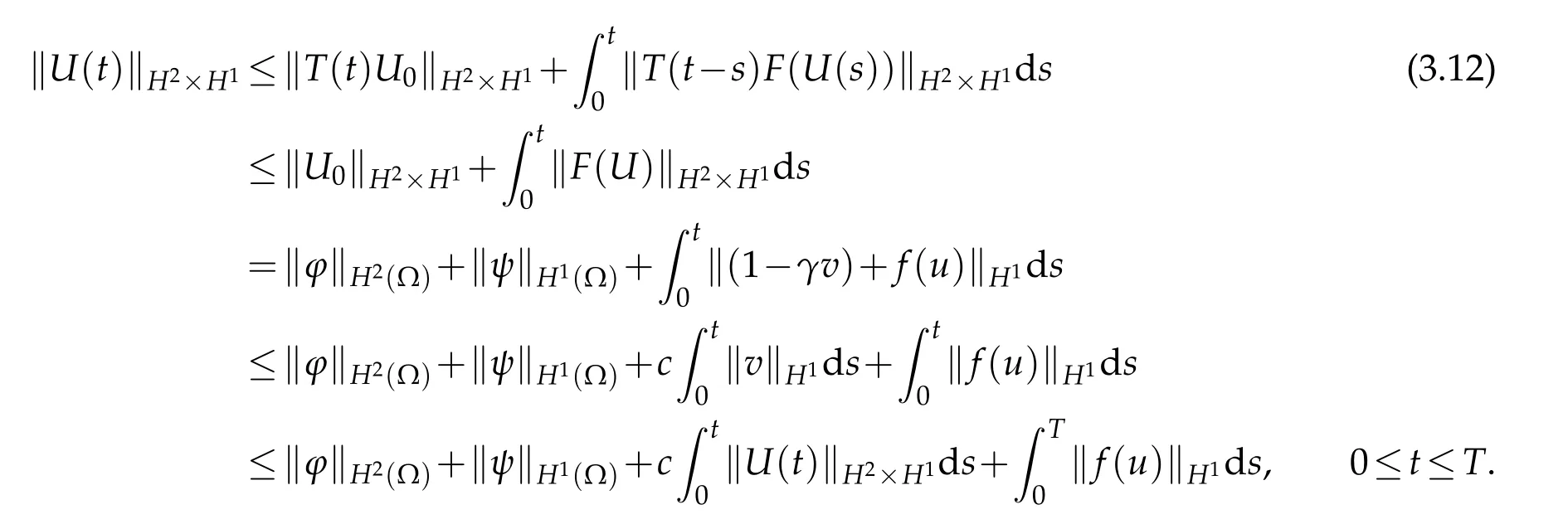
Now,Gronwall’s inequality asserts

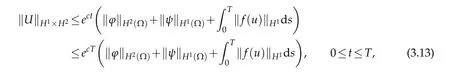
which implies that the estimate(3.3)and the uniqueness follows.

If Ω is a bounded open domain with smooth boundary,in which we can consider the Neumann boundary condition,as we know that thee∆tdefines a holomorphic semigroup on the Hilbert spaceL2(Ω),then

where

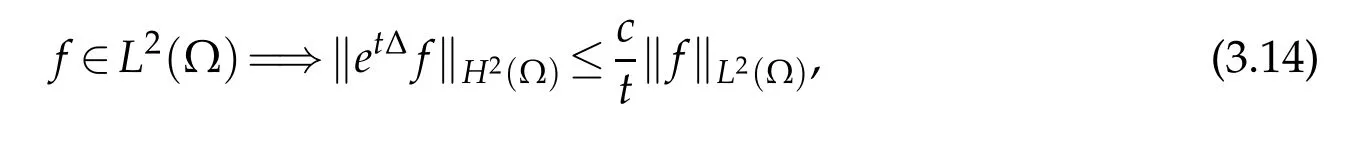
Applying interpolation to(3.14),it yields

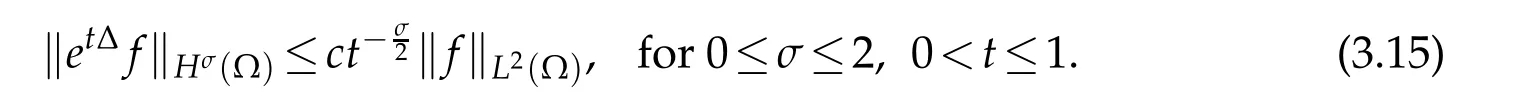
TakingY=andZ=L2(Ω),then forv∈Yt0,and from the proposition in Tylor(1996,p,273),we can declare the following lemma.

Lemma 3.2.For each u0∈Y and v∈Yt0,if σ and N satisfy conditions(2.2)and(2.3),then problem(3.1)has a unique solution

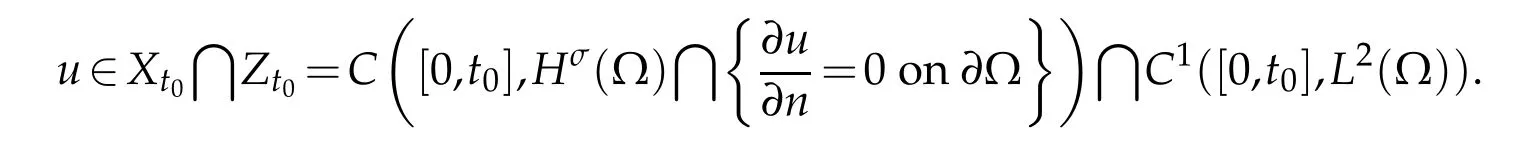
Proof.We consider the following problem first

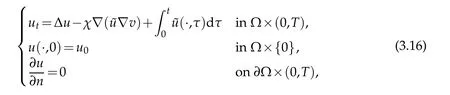
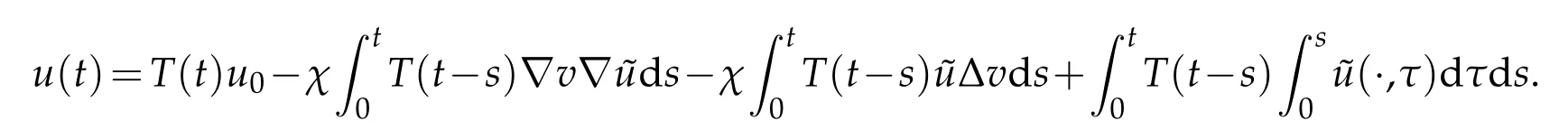
Define a mapping

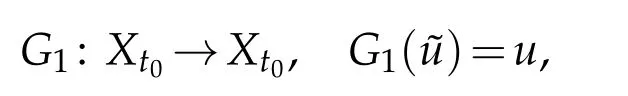
whereuis the corresponding solution of(3.16).

Then we claim that fort0small enough,G1is a contract mapping.In fact,letandu1,u2denote the corresponding solutions of(3.16),we have

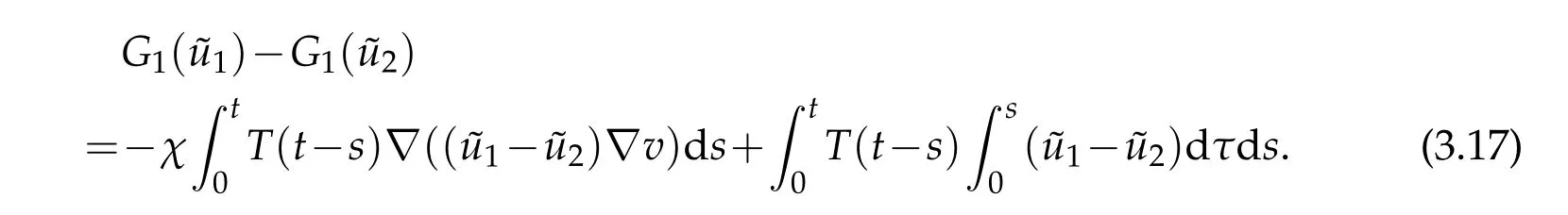
By Sobolev imbedding theorems,we have

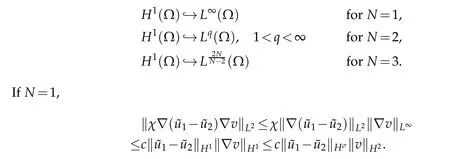
IfN=2,3,according to(2.2)and(2.3),we obtain that

Hence forN=1,2,3,we have

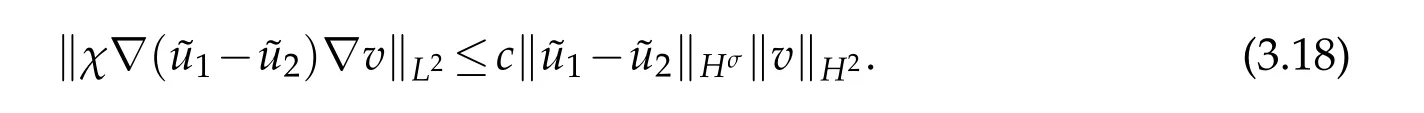
Similarly,we have

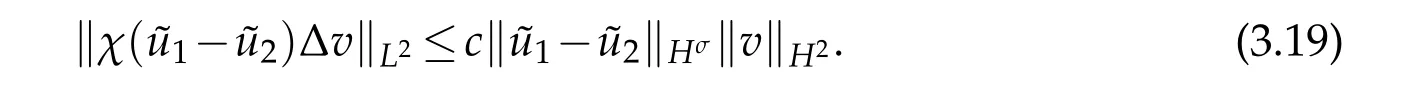
So for the first term on the right side of(3.17),N=1,2,3,by(3.18)and(3.19),we have

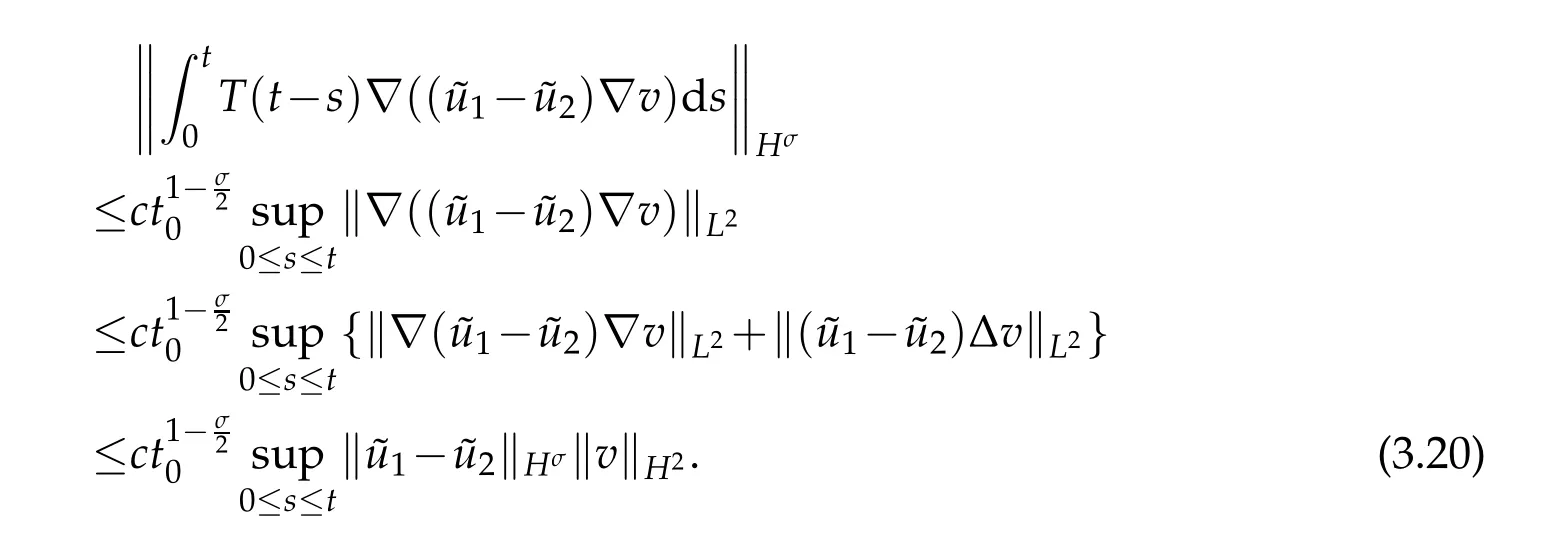
For the second term on the right side of(3.17),we have

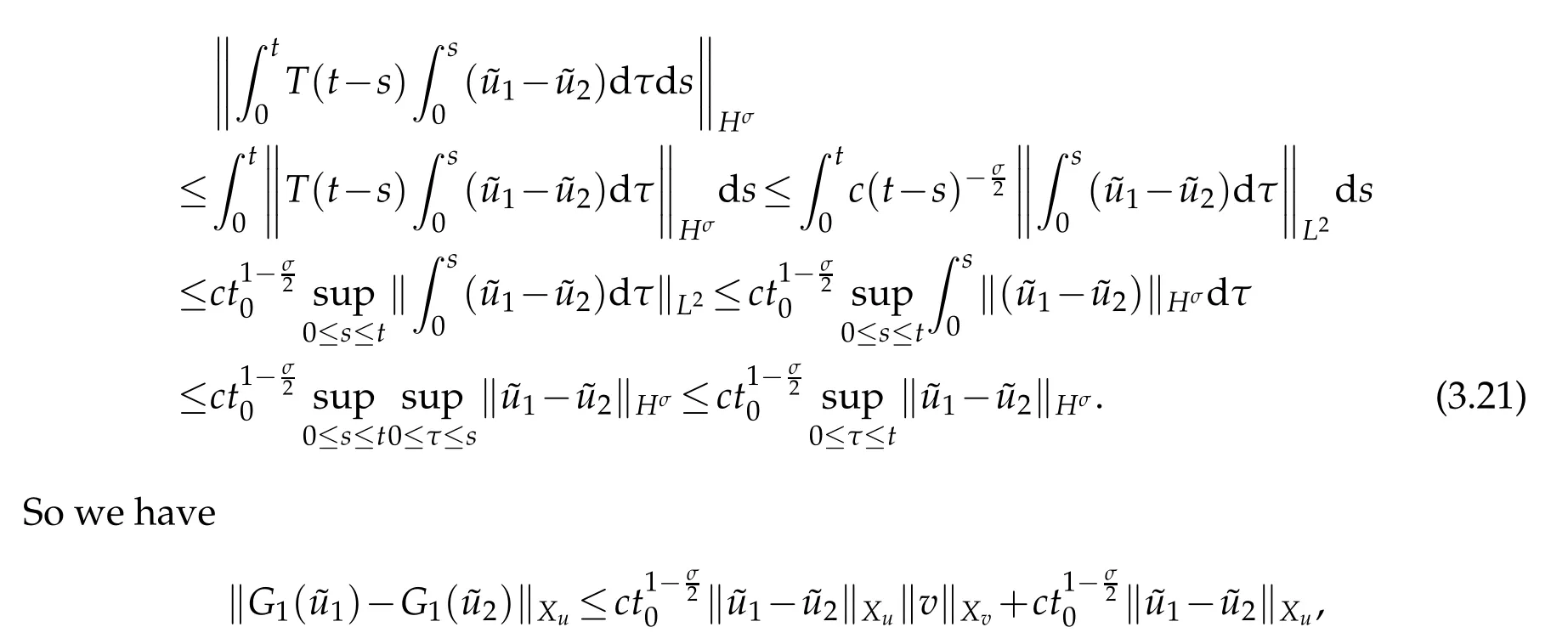
which implies fort0>0 small enough,G1is contract.By Banach fixed point theorem,there exists a unique fixed pointsuch thatso(3.1)has a unique solution,and the solution can be written as

This completes the proof of the lemma.

Lemma 3.3.Under conditions(2.2)and(2.3),if u∈Xt0is a solution of(3.1),then there exists a constant c which is independent of t0such that

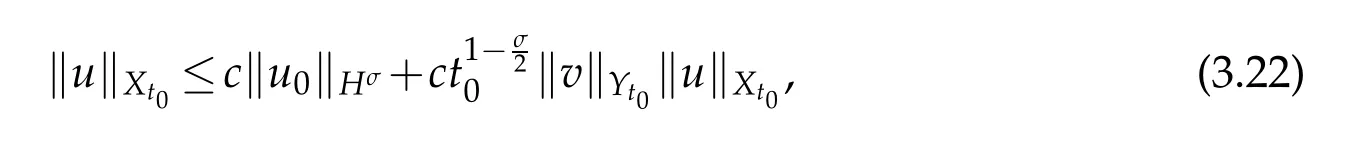
where‖·‖k,p is the norm of Sobolve space Wk,p.

Proof.Acroding to Lemma 3.2

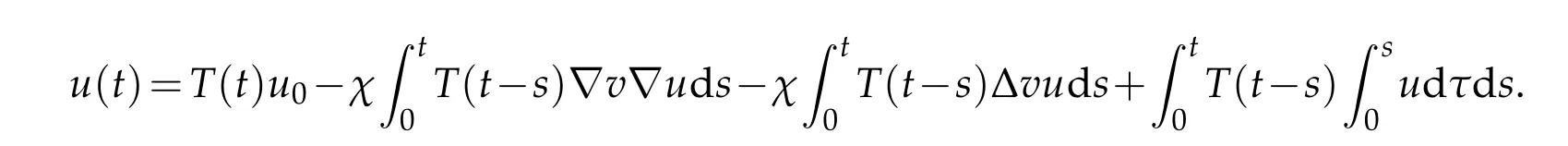
By(3.14),we haveT(t):with norm.Thus

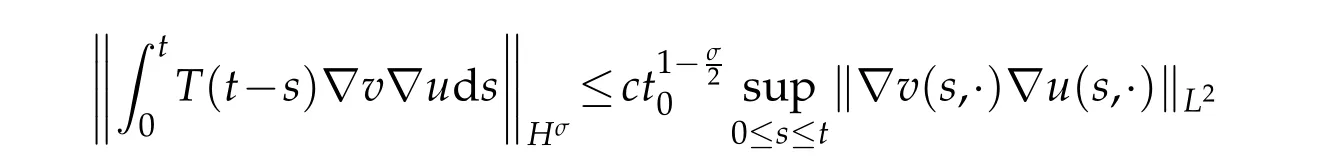
By Sobolve imbedding theorem,forN=1,we have

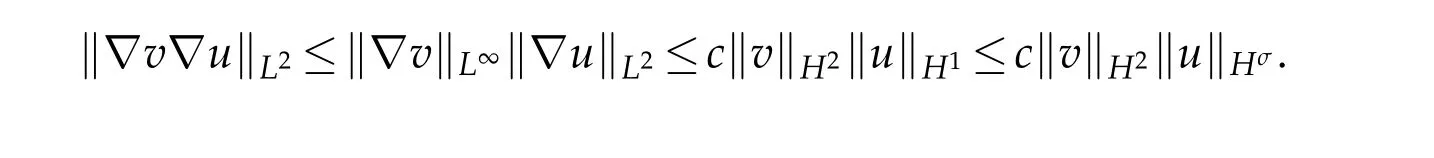
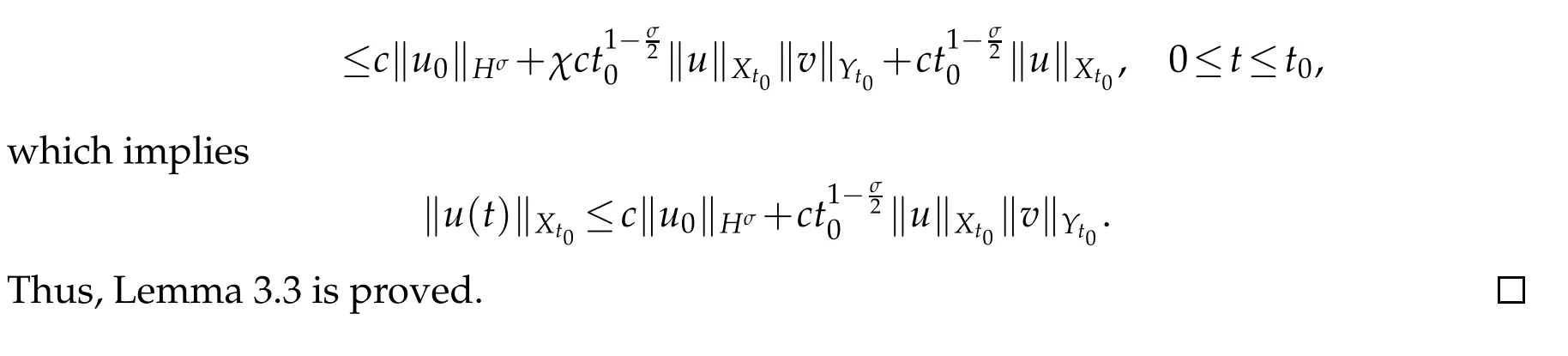
4 Local existence of solution

In this section,we establish the local solution of system(2.1).Our main result is as follows.

Theorem 4.1.Under conditions(2.2)and(2.3),if g(u,v)=−γv+f(u)and f∈C2(R),then for each initial dataproblem(2.1)has a unique local solution(u,v)∈for some t0>0.Proof.Considerandw(0,x)=u0(x) and letv=v(w) denote the corresponding solution of the equation

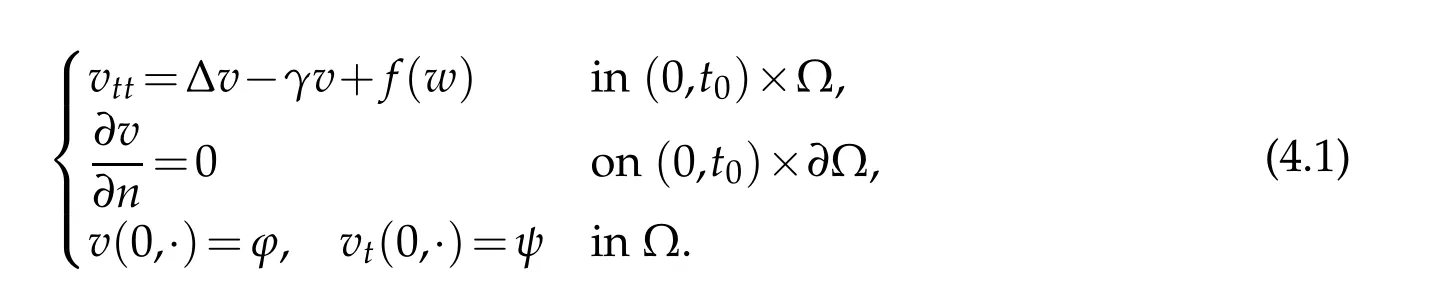
By Lemma 3.1,we haveand

Secondly,for the solutionvof(4.1),we defineu=u(v(w))to be the corresponding solution of

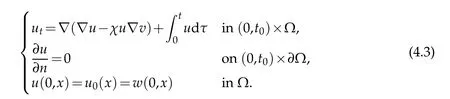
If we defineG2w=u(v(w)),then Lemma 3.2 shows that

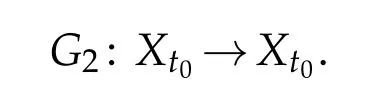
TakeM=2c‖u0‖Hσand a ball

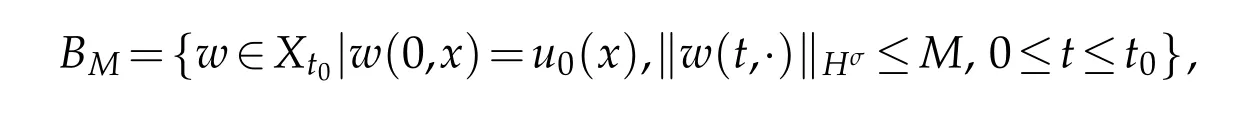
where the constantc≥1 is given by(3.19).Then we conclude from(3.22)and(4.2)that

ifw∈BM,‖w‖H1≤‖w‖Hσ≤Mandf∈C2(R),we can deduce that

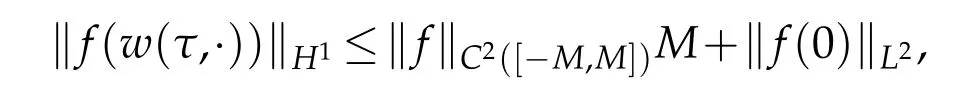
We have proved that,fort0>0 small enough,G2mapsBMintoBM.Next,we can prove that,fort0small enough,G2is a contract mapping.In fact,letw1,w2∈BM⊂Xt0andv1,v2denote the corresponding solutions of (4.1).Then,the differenceG2(w1)−G2(w2)satisfies

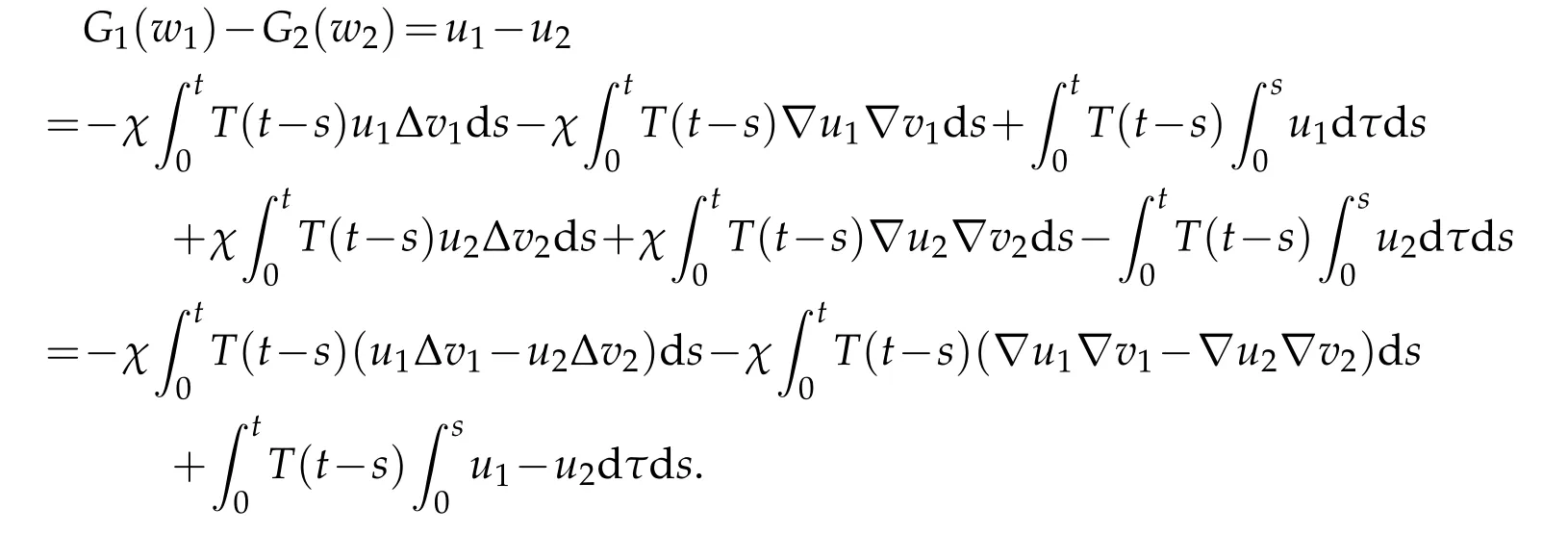
Next,we have

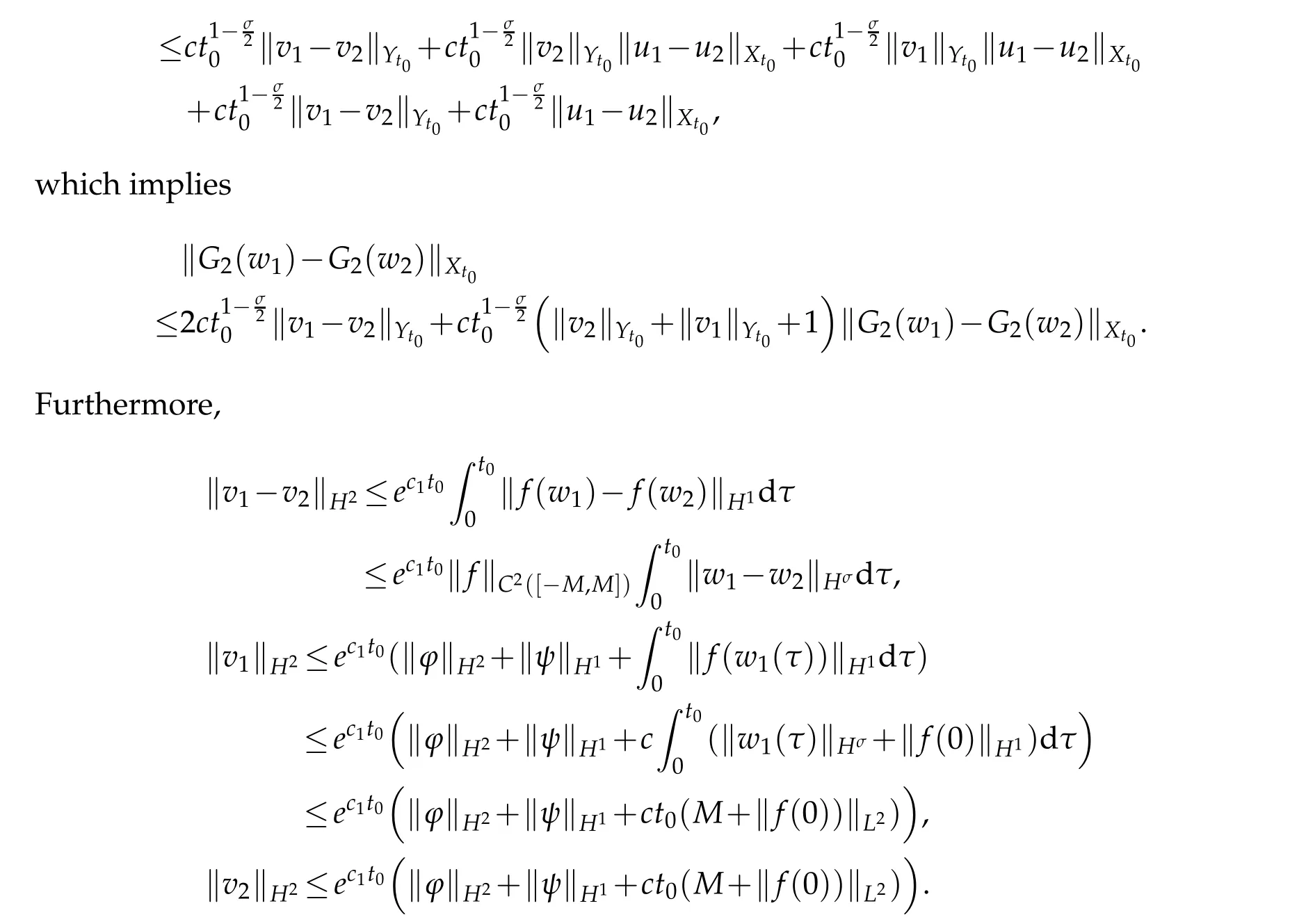
Thus fort0>0 small enough,G2is contract.

From the process above,we have proved that problem (2.1) has a solution (u,v)∈Xt0×Yt0and(u,v)∈Zt0×Wt0by Lemma 3.1 and 3.2.The uniqueness is obvious sinceG2is contract.Thus we have proved the Theorem 4.1.

Acknowledgement

We would like to thank the referees for carefully reading the manuscript and for their helpful suggestions.