基于参数周期李亚普诺夫方程的闭环系统设计
2021-10-23谢琪龙陈扬阳邓小龙刘敏绮刘祎妮
谢琪龙,陈扬阳,邓小龙,刘敏绮,刘祎妮
(1.广西师范大学数学与统计学院,广西 桂林 541006;2.广西师范大学计算机科学与信息工程学院/软件学院,广西 桂林 541006)
0 引言
由Clohessy以及Witshire给出的C-W方程是一个线性时不变方程,在以往研究圆轨上的航天器轨道交会优化控制问题上都取得了较理想的效果。但是以往的研究在基于C-W方程进行航天器轨道交会优化控制设计时,没有考虑现实中进行反馈控制器的参数浮动以及摄动力的存在而引起的参数变化或参数增益。然而在实际操作中,不能包容控制器微小的参数变化的闭环系统必然是不稳定的,而且很有可能是致命的。故本文设计了有界线性时变连续周期闭环系统。使得系统兼备鲁棒性及优良的性能,使得航天器更加核心竞争力[1]。
1 线性有界时变连续周期闭环系统的设计
1.1 相关研究综述
Wada, Asai和Ikeda建立了利用Riccati型微分方程的解设计LTV控制器和LTI系统的非指数镇定,以此来提高控制性能。Cacace, Germani和 Manes 采用了时滞相关时变观测器增益来实现期望的指数误差衰减。指数时间增益用于Ahmed-Ali, Fridman, Giri, Burlion和Lamnabhi-Lagarrigue对样本数据的稳定和估计进行了研究,发现与常数增益相比,最大采样间隔可以相差很大,许多非线性或非完整的机械系统,如普通轮式移动机器人不能通过使用光滑pure-state(纯态)反馈控制来确定。但是其仍然可以通过使用光滑时变反馈来保持稳定性。
周彬博士研究设计的线性时变闭环系统能够实现在有限时间内收敛的研究方法(BinZhou,Finite-time stabilization of linear systems by bounded linear time-varying feedback)对此我们在此基础上进行进一步的改进,将周期这一个重要性质考虑进去,得到一个新的、基于周期李亚普诺夫稳定性理论的线性时变周期闭环系统。
本文通过建立线性有界时变连续周期反馈来实现有限时间内的镇定。在不考虑外部干扰情况下,允许设计一个时变参数存在于反馈增益中,求解参数李亚普诺夫方程来实现控制器的设计。所有设计均有赖于参数李亚普诺夫方程的主要特征,该解对应参数李亚普诺夫方程的一个参数的导数的上界和下界。
据参数李亚普诺夫方程的特性,实现闭环系统收敛速度快于指数,或者调节时间小于正无穷,此时的线性控制器是稳定的(或渐进稳定的)。并有反馈增益k是时变的,控制u(t)在收敛期间保持有界。基于此原理,设计一个收敛速度快于指数且调节时间小于正无穷的有界线性时变连续周期反馈系统。
本文考虑航天器姿态定向保持并姿态镇定,考虑目标航天器在偏向率较小的低地球轨道运动,并且目标航天器与追踪航天器相距不远(≤50km)的交会情况。
我们考虑一个非线性相对运动模型:
其中,旋转目标航天器的轨道旋转坐标系统如图一所示:
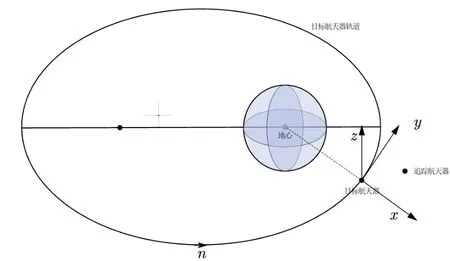
图1 旋转目标航天器的轨道旋转坐标系
其中,坐标原点为目标航天器的质心,x-轴在从地心到目标航天器的质心的直线上,y-轴在沿着目标航天器轨道的切线方向上,z-轴与x-轴、y-轴构成右手系。 并且坐标系以地球的质心为圆心,R为轨道半径,n为轨道角速度进行周期旋转。
本文考虑航天器姿态定向保持并姿态镇定,考虑目标航天器在偏向率较小的低地球轨道运动,并且目标航天器与追踪航天器相距不远(≤50km)的交会情况。
对于上面的航天器交会模型,我们可以得到以下的非线性相对运动模型:
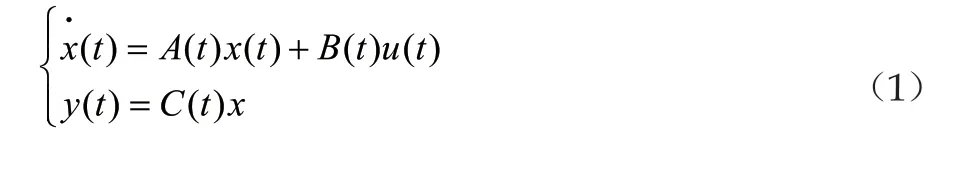
首先考虑预控制器u(t),对其进行参数化反馈,有
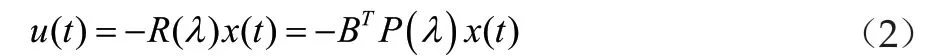
将闭环系统收敛参数λ设为随着时间变化的,是一个关于时间t的函数。即λ表示闭环系统的收敛速度,而且我们有P(λ)为参数李亚普诺夫方程的一个矩阵解。
若参数李亚普诺夫方程考虑应用在周期控制系统的设计上,由周彬博士研究论文[2](具有饱和非线性的控制系统研究的参数Lyapunov方法及其应用)可得参数周期方程对于参数周期李亚普诺夫方程,存在一个P(λ)为其通解。假设P(λ)>0,则系统(1)以及预控制器(2)组成的闭环系统轨迹上的时间导数满足以下方程
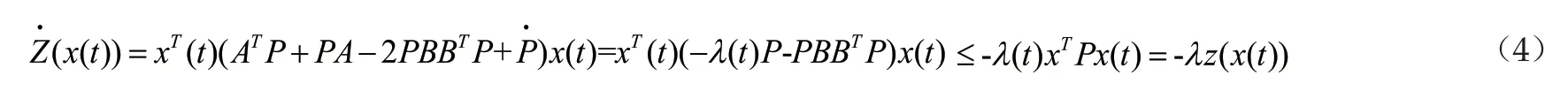
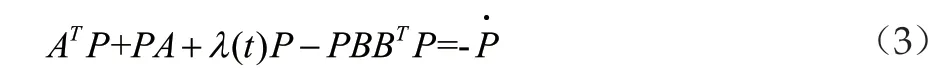
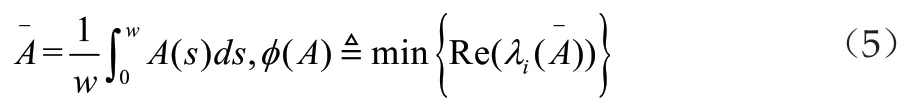
下面我们将需要证明我们的参数解P(λ)是满足如下的一个形式的一个矩阵,从而知道该解是合适的。
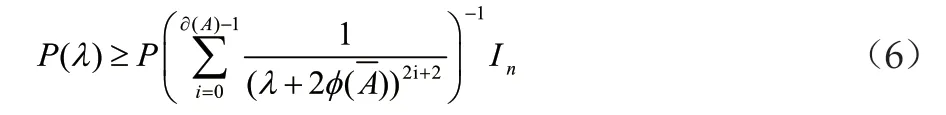
1.2 状态反馈
考虑设计时变反馈系统,以预控制器(2)的反向增益形式,实现收敛速度比指数快的收敛。首先选择一个类参数李亚普诺夫方程的函数,设计一个λ(t),使得x(t)在在有限时间内收敛于零;与此同时,保证预控制器u(t)在收敛过程中有界。
(1)闭环收敛速度参数λ(t)的寻找。对于上文中所要求设计的时间T,我们可以将其表示为如下形式

其中我们对其中的参数进行定义

通过以上的定义,可以知道时间T是小于一个周期w的,即
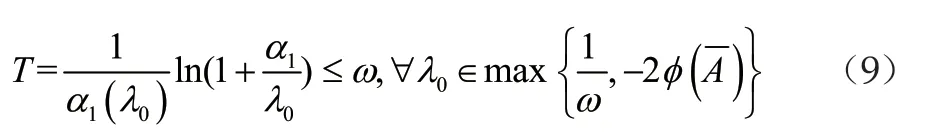
给定关于λ的一个合理解集,通过给出该解集,我们对λ的取值进行限定
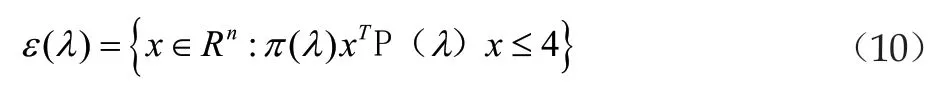
考虑下面的有界线性时变状态反馈

利用该状态反馈,我们可以得到一个形如方程(5)的一个证明,其中σ是一个常数。
对于参数周期李雅普诺夫方程(3)的一个参数解λ,给出如下的形式:
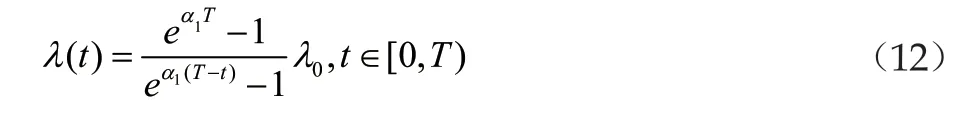
通过验证可以知道它是满足一个微分方程的解的形式
系统参数满足以下不等式关系:
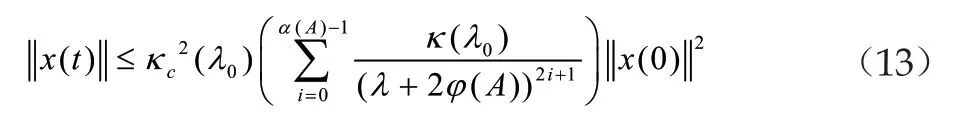
即ε(λ)包含在闭环系统里,其中是一个关于的一个函数表达式。由预控制器(2)和系统(1)组成的闭环系统使得包含在闭环系统的引力域内。
(2)预控制器u(t)在收敛过程中有界。在实际进行航天器控制中,u(t)应存在一个控制上界。考虑在设计轨道控制器的时候,设计控制器使之可容许控制输入尽可能的小。使得系统(1)在较小的控制输入下,其状态可逼近原点。
考虑基于观测输出反馈情况,设计一个可观测的控制器,其形式如下
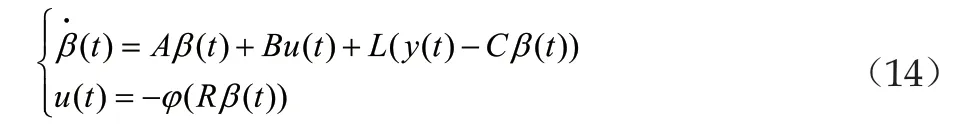
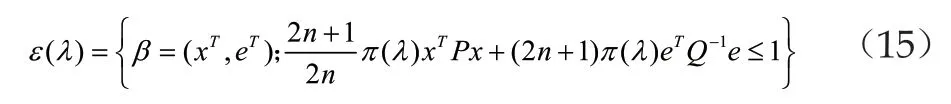
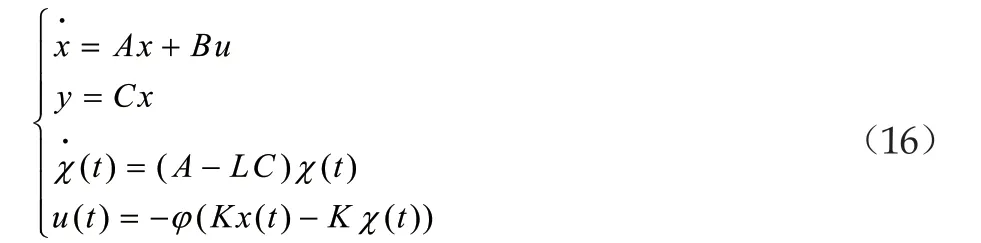
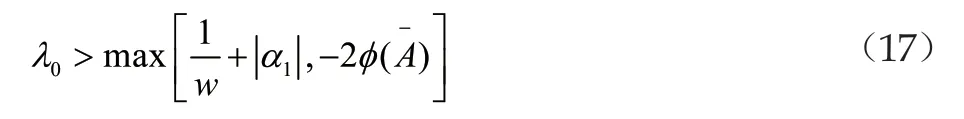
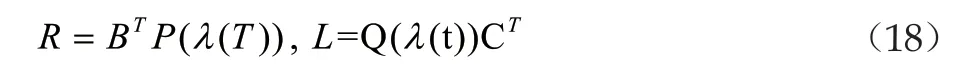
其中,T为给定的有限常数,并且我们通过重新设计T,可以得到T的一个如下表达形式:

T的取值此时应该与系统的一些初始参数相关,它与参数λ0、α1不再满足一定的指数关系,而是满足一个对数关系表达式[4]。此时,相应地可以得到闭环系统的收敛参数λ满足如下形式
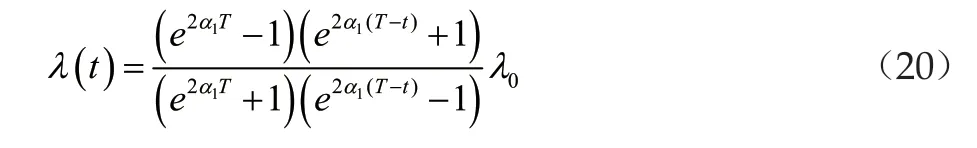
从而可以得到收敛参数λ是满足等式

并且可以知道它是快于指数收敛的。通过相应的验算可以由李亚普诺夫方程的稳定性理论得到,由系统(1)和基于观测的反馈控制器(2)组成的闭环系统(14)是渐进稳定的。
2 结语
本文基于C-W方程的航天器交会的非线性相对运动模型,依据参数李亚普诺夫方程及其稳定性理论,通过对其解及其性质进行研究,得到了由航天器系统和预控制器组成的闭环系统。并根据参数李雅普诺夫方程的稳定性理论结合周期理论建立相关的类参数里亚普诺夫方程,并以此作为核心依据,进行航天器闭环系统预控制器的设计。通过一些向量标量的手段,能够很好的证明所设计的系统是稳定的而且是合理的,能够满足所有的稳定性要求。通过对参数周期李亚普诺夫方程性质的研究,能够证明闭环系统状态,即其参数可以在有限时间内实现渐进收敛,并且设计的系统是由系统参数和初始条件所决定的。
自此我们得到了所求的控制系统,并证明所给系统的稳健性。本文所提出的闭环设计方法可以应用在航天器轨道交会控制系统中。应用此方法进行航天器系统的设计可以使得该航天器的闭环系统具有鲁棒性。
