有限长序列线性相关的快速算法研究

刘志君，戚晨皓

（1.东南大学 吴健雄学院，江苏 南京211189；2.东南大学 信息科学与工程学院，江苏 南京211189）

0 引言

在“数字信号处理”中，相关是一个十分重要的信号分析与处理的工具，在时延估计、随机信号的统计特性分析以及随机信号的功率谱估计等方面有着重要的应用［1］，例如平稳随机信号的功率谱密度就是其自相关函数的傅里叶变换［2］。因此计算两个有限长序列的线性相关是十分重要的内容，而相关文献对于线性相关的FFT算法研究甚少，所以有必要对其快速运算作一些探讨和研究，特别是长序列数字信号处理的快速算法，以期达到实时性的目的［3］。本文首先介绍了已有的直接FFT算法快速计算线性相关，而当两序列长度相差较大时，直接FFT算法的快速性不够明显，因此本文重点研究了如何利用分段求和FFT算法来计算线性相关，该算法相比于直接FFT算法显著减少了运算量。

1 直接FFT算法计算线性相关

1.1 直接FFT算法

设两有限长序列x（n）、h（n）的长度分别为N、M，则x（n）与h（n）之间的线性相关的结果（又称互相关函数）rxh（m）和rhx（m）定义为：

观察式（1）和（2）我们可以发现两种不同互相关函数之间的关系：

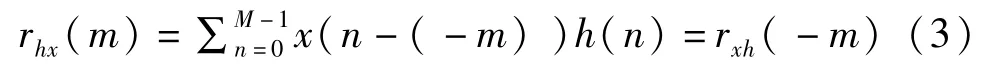
根据定义可以发现，互相关函数的长度为N+M-1，且两个有限长序列的互相关函数有两个［4］，但是二者之间有明显的关联性，即rhx（m）=rxh（-m）。如果直接使用定义计算线性相关，其运算量为NM次乘法，时间复杂度为O（NM）。

为了利用FFT快速计算线性相关，我们需要用到线性卷积的相关内容［2］，将rxh（m）的公式与线性卷积的公式相比较，可以得到二者的时域关系为：

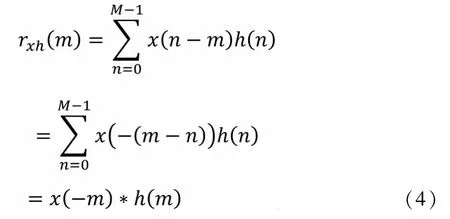
根据式（4），我们就可以利用线性卷积的FFT算法［1］快速计算线性相关。这里我们还需要用到循环相关的概念，对于长度分别为N和M的有限长序列x（n）、h（n），其L点循环相关的结果（L≥max｛N，M｝）定义为：

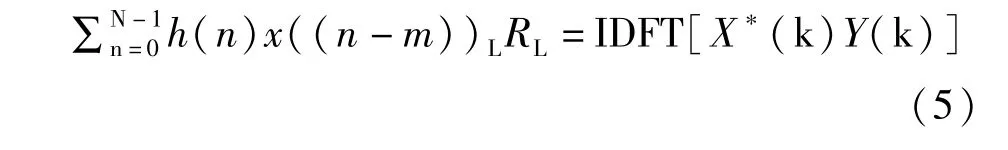
式（5）中：（（·））L表示对L求余数，RL（n）为矩形序列，X（k）与Y（k）均为L点FFT的结果。

循环相关和线性相关的等价关系［1］为L≥N+M-1，故直接FFT算法计算线性相关的过程如下：①取L=N+M-1；②对x（n）和h（n）做L点FFT得到X（k）与H（k）；③然后将X*（k）与H（k）相乘得到Rxh；④对R做L点IFFT得到。

从上述过程来看需要3次FFT运算，但是在实际运用中，h（n）是设计好的参数，在设计时直接给出H（k），因此只需要2次FFT计算和第三步的L次乘法，因此得到直接FFT算法的运算量为（Llog2L+L）次乘法［1］，时间复杂度为O（Llog2L）。

1.2 直接FFT算法运算量的改进

前文讨论线性相关的运算时并没有考虑到N和M的关系对于直接FFT算法改进程度的影响。因此需要定义一个比值

通过式（6）来讨论N和M的关系对于直接FFT算法改进程度的影响［3］。根据已经得到的运算量的结果我们可以得到：

当N≈M时，可近似认为L=N+M-1≈2N，将两种算法的运算量进行比较（表1）。

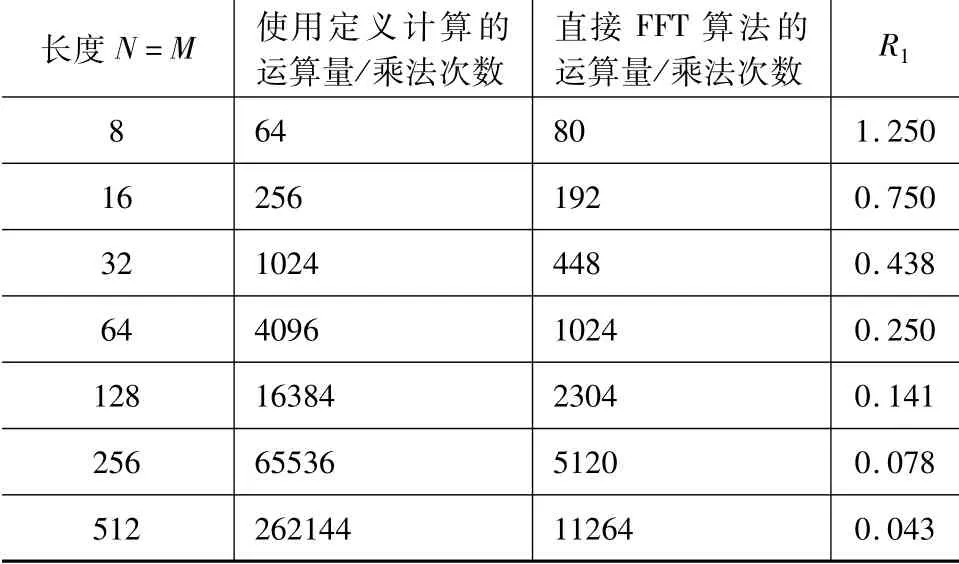
表1 N与M接近时运算量的比较

从表1中可以看出，当N=M时，N越大，直接FFT算法的运算量改善效果越好，在N=M≥16时，直接FFT算法的运算量就已经明显小于使用定义计算的运算量。

但是在实际的信号处理中，两序列的长度相差较大，一般数字信号处理的单位冲激响应h（n）较短，而数字信号x（n）的长度较长。如果使用直接FFT算法进行计算，h（n）必须补很多个零值点，这样一来很不经济，二来快速性不明显［3］。在式（7）中，如果N≫M，可以近似认为L=N+M-1≈N，此时，如果M不变，随着N增加到大于2M，R1值反而会增大到超过1，这意味着直接FFT算法不仅没有起到显著减少运算量的作用，反而会在N大于2M时增加运算量，这是我们所不期望的，因此需要改善FFT算法，这就是以下将重点介绍的分段求和FFT算法。

2 分段求和FFT算法计算线性相关

2.1 分段求和FFT算法

对于FFT算法来说，先分段计算最后求和是一种很典型的改进计算量的方法［1］，其核心就在于将一部分乘法变为加法，从而达到减小计算量的目的，因此我们考虑设计分段求和FFT算法来快速计算长度相差较大的两序列的互相关函数。

之后利用直接FFT算法分别计算xi（n）与h（n）的互相关函数rxih（n），但是每个rxih（n）的长度都为2M-1，而最后需要得到的结果rxh（m）长度为N+M-1，如果计算补零后的长度则为+M-1=（k+1）M-1，因此在最后求和时，相邻两个rxih（n）必然有（M-1）个点的值要重叠相加。

图1 重叠相加和排列过程

根据求解过程可以得到分段求和FFT算法总的运算量为k（W log2W+W）次乘法，其中W≜2M-1，时间复杂度为O（N log2M）。

2.2 分段求和FFT算法运算量的改进

为反映分段求和FFT算法的改进程度，我们再定义一个比值：

根据已经得到的运算量的结果我们可以得到：

当N≫M时，可近似认为L≈N，N≈=kM，将两种算法的运算量进行比较（表2）。

从表2中可以看出，当N≫M时，如果M不变，N越大，分段求和FFT算法的改善效果越好。在N=7，M=2，即x（n）长度约为h（n）长度的4倍时，分段求和FFT算法的运算量与直接FFT算法的运算量相当。

在N=15，M=2，即x（n）长度约为h（n）长度的8倍时，分段求和FFT算法的运算量就已经明显小于直接FFT算法的运算量。

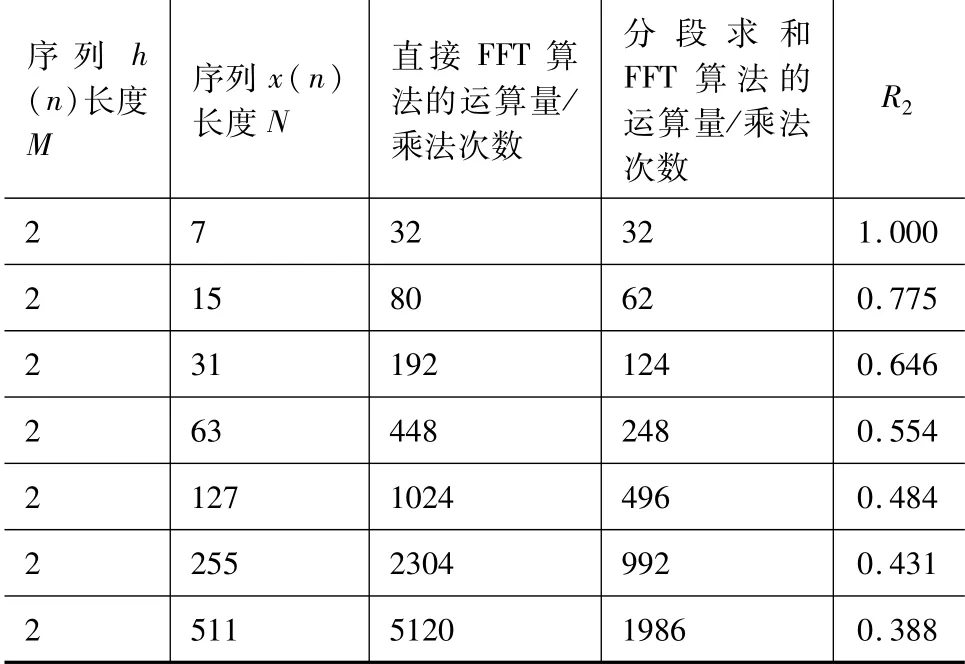
表2 N远大于M时运算量的比较

3 结语

本文重点研究了如何利用FFT快速计算两个有限长序列的线性相关，介绍了直接FFT算法及其运算量的改进，以及当两个序列长度相差较大时分段求和FFT算法及其运算量的改进，并综合比较了两种算法的运算量。结果表明，相比于根据定义直接计算线性相关，直接FFT算法显著减少了运算量，且序列长度越长，改善效果越明显；若参与线性相关的两个序列长度相差较大，则相比于直接FFT算法，分段求和FFT算法具有更小的运算量，且序列长度差距越大，改善效果越好。